LabVIEW Programming Contest. The decision of the winning team
Computer games about tanks are among the most popular in the game-industry. The history of such games has been around for decades, but their popularity has not faded. The theme of tanks and tank battles is being developed not only in computer games, but is also the subject of a competitive programming process. For example, in 2012, there were programming competitions Russian AI Cup - CodeTanks . Participants were asked to develop an artificial intelligence control tank. A few years later, a similar competition repeated. The organizer was the company National Instruments, which annually holds LabVIEW programming contests among students and young scientists. Participants in the 2015 Olympiad were asked to develop an algorithm for autonomous control of a tank using LabVIEW tools (you can get an idea of this programming environment at the link: “LabVIEW is the first acquaintance” ). This article describes the algorithm of the winning tank from the LabVIEWPortal team.
A team of representatives of the community of like-minded LabVIEWPotral traditionally takes part in the competition of programmers. In 2011, the performance was successful - the team took the 1st place . In the Olympiad 2015, the team managed to repeat its success. From the portal was formed a team of three people. Some difficulty was the territorial distance, because the team members live in different cities and time zones. But we must look not for problems, but for solutions, with which the team successfully coped.
The players in turn are passed the following parameters:
1. Parameters of the battlefield (dimensions, description of obstacles: coordinates of the extreme points of obstacles and their remaining strength);
2. Parameters of the tank (dimensions, speed of rotation of the hull and turret, movement, speed of shells, etc.);
3. Description of the shells fired at the moment (coordinates of the current position of the projectile, velocity vector and the number of the player who fired the projectile);
4. Description of obstacles (an array of coordinates of the extreme points of obstacles and their remaining strength);
5. The current state of the tanks (the coordinates of the center of the hull, the angles of rotation of the hull and turret, the remaining strength and the remaining recharge time);
For a certain time slot, the player must make a decision and indicate the action for the tank hull (movement or rotation), the relative angle of rotation of the tank turret, and also indicate whether a shot is required. If the decision is not made in the allotted time, the work of the player’s function is interrupted and the move goes to another player. The winner is either the one who managed to destroy the enemy tank, or the one who has more safety margin than the enemy after the allotted time per round. Damage is inflicted exclusively by shells (when tanks collide with each other or with walls, no damage is caused). Battle mode: one on one, maps for battles are not known in advance.
')
One of the first tactics of combat was continuous fire and moving along the shortest path to the enemy, bypassing the walls. But, after analyzing the speed among some popular path finding algorithms (wave algorithm, convex polygon method, A * search algorithm), we came to the conclusion that our tank may not have time to calculate the trajectory of movement with subsequent analysis of the situation. This tactic had to be abandoned in favor of a simpler option: “wait, shoot and maneuver.”
Wait, shoot : from the initial position we shoot at the center of the enemy, regardless of the walls, since they are gradually destroyed by shells. Each turn adjusts the position of the tower so that it looks exactly in the center of the enemy.
Maneuvers : we place the hull perpendicular to the line of fire. From this position to avoid enemy shells is easiest. In this regard, each turn, in the absence of danger, we adjust the angle of rotation of the body. Accordingly, the evasion maneuver consists in rolling the tank back or forward. The choice of direction depends on the place of intended hit: the front or rear of the tank.
However, in the course of preliminary competitions, two significant deficiencies of the strategy were discovered:
These deficiencies were eliminated by adding several checks and conditions:
Regardless of the mode, adjust the angle of the hull so that it is perpendicular to the line of fire (the line connecting the centers of the tanks).
General view of the program code:

At the preliminary stage of the analysis of the initial data (before the main cycle is completed), the destroyed walls and their projectiles are screened out. The following is a choice of strategy. If you are in a danger zone, then
If the enemy has disappeared behind the wall, then we will not return to safe mode, since the rotation of the tower to the nearest wall and back takes time, and an extra waste of time in combat conditions is unacceptable.
If the zone is safe, then we perform two checks:
1. The number of walls between the tank and the enemy;
2. The number of walls between the tank and each of the shells.
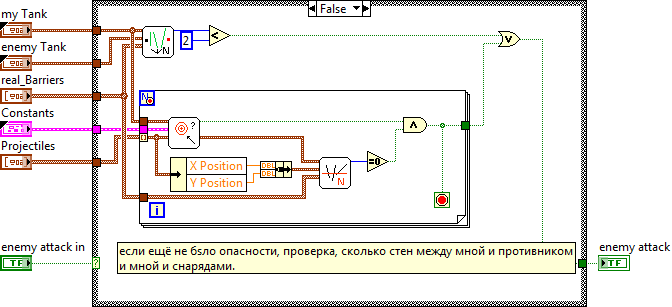
One wall is chosen for security reasons: if there are few “shields” left, then you must turn the tower on the enemy in advance to save time. Checking the walls between the tank and the enemy is shown below and uses the same function as checking the walls between the tank and the projectile (only different ends of the segments).
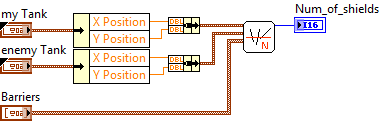
The function of searching for the number of “shields” is described below.
Projectiles are looped through, but the projectile hazard check is conducted at the point of impact, and not at the center of the hull. Reason: "tricky" enemy shooting from around the corner.
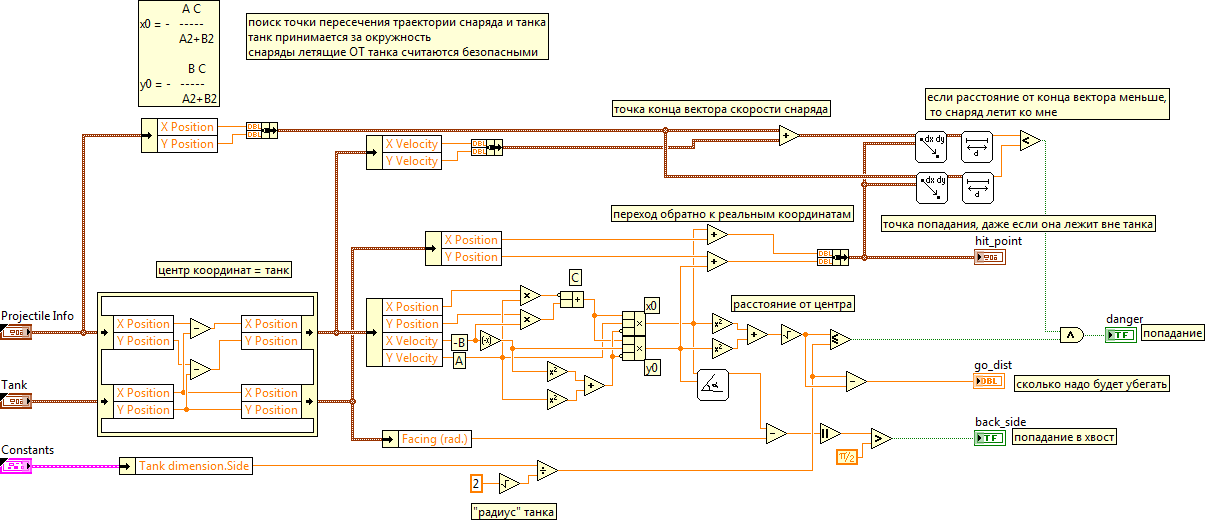
To simplify the calculations, the tank is considered as a circle described around the hull. The point of contact is taken at the point of intersection of the trajectory line of the projectile and perpendicular from the center of the tank to this line. In addition, the origin is transferred to the center of the tank.
For the straight line Ax + By + C = 0, the point of the perpendicular from the origin is calculated by the formulas:
x0 = - AC / (A ^ 2 + B ^ 2)
y0 = - BC / (A ^ 2 + B ^ 2)
Since the origin of coordinates in the center of the tank, then to check the hit it is necessary to calculate the length of the segment [(0,0) (x0, y0)]. If the length is less than the "radius" of the tank, then the projectile is dangerous.
Then calculate the distance that you need to roll back when maneuvering from the projectile (it will be needed later).
Next is determined by the area of contact: the front / rear of the tank. To do this, calculate the angle at which the straight line ((0,0) (x0, y0)) is located relative to the axis 0x. To simplify calculations (similar angles will be required in the future) are used.
If the angle between this straight line and the direction of movement of the tank is less than pi / 2, then hit the front, otherwise - in the rear.
The last check that needs to be done is whether the projectile is flying into our tank. The first version of the tank did not take into account the direction of flight, and the tank tried to escape from the safe projectiles.
The check is performed as follows: since the projectile is specified by the beginning and length of the vector (componentwise), this allows to calculate the distance from the beginning of the vector to the center of the tank and from the end of the vector to the center of the tank. If the end of the vector is closer to the tank, then the projectile is flying in our direction.
Next, it is checked how many wallboards there are. Verification is carried out on all shells, including safe projectiles.
Each wall is a segment. Another segment is constructed between the center of the hull or the point of impact and the center of the enemy or projectile. Further, it is checked whether these segments intersect. The verification algorithm is taken from the article at the following link: grafika.me/node/237 . Its essence lies in the analysis of vector products of vectors connecting different ends of segments.
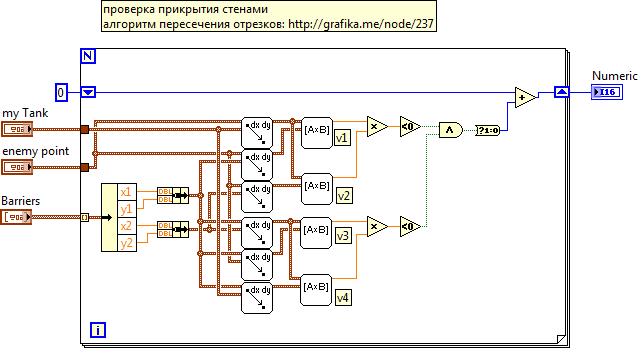
All walls are checked in a cycle, the first dangerous projectile is considered a breakpoint: since the situation is already dangerous, there is no sense in checking further. Thus, if less than two walls remain before the enemy, or a shell (not covered by walls) flies into the tank, then it is necessary to attack, otherwise destruction of the nearest walls for future maneuver continues.
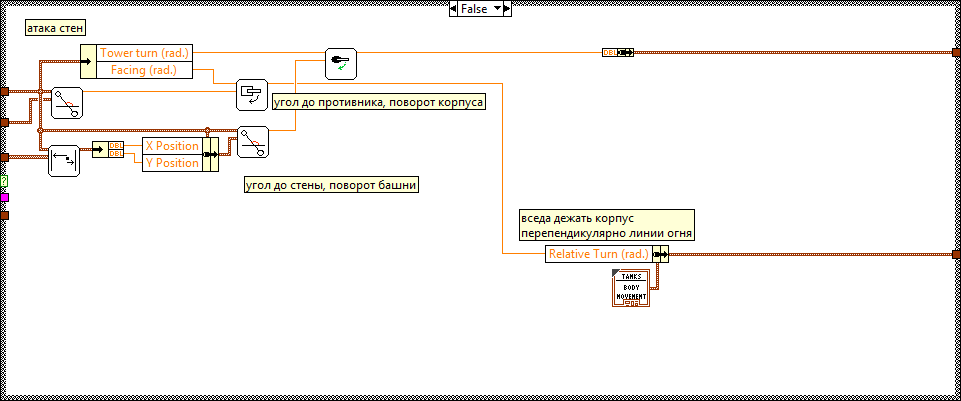
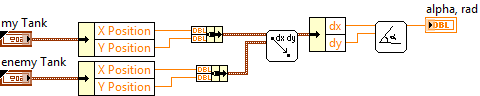
First, the angle of rotation of the body is corrected. Then the angle of the “tank-enemy” straight line is determined with the x axis, using the functions of finding the vector and its angle with the Ox axis already described.
Determination of the angle of the body turn is as follows:
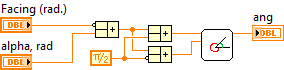
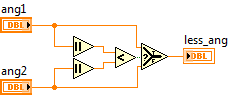
From the two corners the smallest one is chosen, since the “right-left” is not important here.
It is worth noting that, as in the case of shooting, the system (arbiter program) indicates the desired action: turn at once to the whole angle, make a shot. Then the system performs the permissible part of the desired: permissible rotation, shot (if the gun was reloaded).
In parallel, the distance from the center of the tank to all walls is calculated and the smallest value is selected.
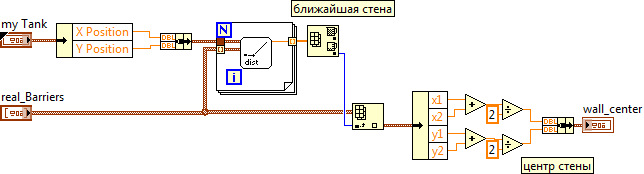
After selecting a wall, its center is determined, where the shooting will take place. It should be noted that there may be several minima, but the system will issue the first in order. After the destruction of one wall (green direction), the next nearest one is selected. In theory, it may be blue (suppose that the distances are equal), but the next in order may be the far wall (red line), and the tower will turn for a long time to it, with several shots going to other walls. If you wish, you can modify the choice so that the nearest to the cannon is selected from the nearest walls.
The distance to the wall is the distance from the point (center of the tank) to the segment. It should be borne in mind that sometimes the nearest point will be the point of intersection of a given segment by a perpendicular, and sometimes one of the ends of the segment.
We use the scalar product of vectors, the sign of which gives information about the directionality of the vectors (the entire algorithm is written in the code commentary).

Further, the angle between the axis Ox and the connecting segment is determined (only the others are segments), and then the angle of rotation of the tower is calculated:
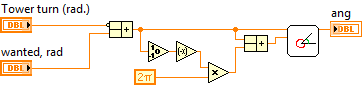
Further, it is checked where the turn is closer: clockwise or counterclockwise.
The angles of rotation of the hull and the tower are calculated by the previously described methods. Further, the first dangerous projectile is located and the “best” side is maneuvered taking into account the point of impact of the projectile. However, it is necessary to verify that there are no obstacles to the retreat. If there are no dangerous projectiles, we rotate the body.
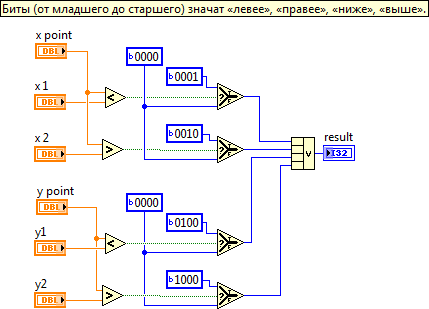
The distance to travel was calculated when checking the danger of the projectile. We denote the current position of the tank black, and the final position gray. Thus, a rectangle is obtained, the side faces of which are the side faces of the tank hull, and the front faces are the current and desired position of the front part of the hull (blue frame). It is necessary to determine if this rectangle intersects any of the segments that define walls.

To determine the intersection, the Cohen-Sutherland algorithm is used, the description of which can be found in this link: ru.wikipedia.org/ Cohen's algorithm_ — Sutherland). To simplify the task, perform the following actions:
Thus, the rectangle, the verification of which must be done:
Next, you need to rotate and move all the segments of the wall when checking. Each wall is checked separately.

Now the position of the “right”, “left”, “above”, “below” points relative to the rectangle is determined by comparing the components x and y separately with the borders of the rectangle.
If an intersection has been found, the check is completed and it is impossible to move in this direction, and for exactly the chosen speed sign we give “full throttle”.
The proposed program code does not claim to be optimal due to the fact that the development, testing and debugging process took a short time. It should also be noted that some of the algorithms were taken from the head, some from the Internet and the team in no way encroaches on the authorship of the algorithms used. In the process of battles, the tank sometimes behaved not quite according to the algorithm - it “stuck” to the wall. Despite this, the intelligent tank control system from the LabVIEWPortal team proved to be the best and took the first place in the Olympiad. Playlist with video of the main fights of the tournament can be viewed at: www.youtube.com/playlist?list=PLKDkvzW_BvvH36vPdeiGKRvmhcZrjMseD
Thank you for your interest, we will be glad to hear your feedback.
About the team
A team of representatives of the community of like-minded LabVIEWPotral traditionally takes part in the competition of programmers. In 2011, the performance was successful - the team took the 1st place . In the Olympiad 2015, the team managed to repeat its success. From the portal was formed a team of three people. Some difficulty was the territorial distance, because the team members live in different cities and time zones. But we must look not for problems, but for solutions, with which the team successfully coped.
Input data
The players in turn are passed the following parameters:
1. Parameters of the battlefield (dimensions, description of obstacles: coordinates of the extreme points of obstacles and their remaining strength);
2. Parameters of the tank (dimensions, speed of rotation of the hull and turret, movement, speed of shells, etc.);
3. Description of the shells fired at the moment (coordinates of the current position of the projectile, velocity vector and the number of the player who fired the projectile);
4. Description of obstacles (an array of coordinates of the extreme points of obstacles and their remaining strength);
5. The current state of the tanks (the coordinates of the center of the hull, the angles of rotation of the hull and turret, the remaining strength and the remaining recharge time);
For a certain time slot, the player must make a decision and indicate the action for the tank hull (movement or rotation), the relative angle of rotation of the tank turret, and also indicate whether a shot is required. If the decision is not made in the allotted time, the work of the player’s function is interrupted and the move goes to another player. The winner is either the one who managed to destroy the enemy tank, or the one who has more safety margin than the enemy after the allotted time per round. Damage is inflicted exclusively by shells (when tanks collide with each other or with walls, no damage is caused). Battle mode: one on one, maps for battles are not known in advance.
')
Strategy development
One of the first tactics of combat was continuous fire and moving along the shortest path to the enemy, bypassing the walls. But, after analyzing the speed among some popular path finding algorithms (wave algorithm, convex polygon method, A * search algorithm), we came to the conclusion that our tank may not have time to calculate the trajectory of movement with subsequent analysis of the situation. This tactic had to be abandoned in favor of a simpler option: “wait, shoot and maneuver.”
Wait, shoot : from the initial position we shoot at the center of the enemy, regardless of the walls, since they are gradually destroyed by shells. Each turn adjusts the position of the tower so that it looks exactly in the center of the enemy.
Maneuvers : we place the hull perpendicular to the line of fire. From this position to avoid enemy shells is easiest. In this regard, each turn, in the absence of danger, we adjust the angle of rotation of the body. Accordingly, the evasion maneuver consists in rolling the tank back or forward. The choice of direction depends on the place of intended hit: the front or rear of the tank.
However, in the course of preliminary competitions, two significant deficiencies of the strategy were discovered:
- In some cases, the maneuver from the projectile led to a "ride into the wall."
- Some walls interfered in general for maneuvering.
These deficiencies were eliminated by adding several checks and conditions:
- Safe mode If there is more than one wall between a tank and an enemy, then we shoot the nearest wall, which is not necessarily lying in the way. This is an important point, because it is not known how the body will be turned when the enemy leaves the open line of fire.
- Dangerous mode . If there is less than 2 walls between the tank and the enemy, turn the tower to the center of the enemy and continuously shoot.
- Evasion . If an enemy projectile flies into the tank, then we calculate the point of impact: the “front / rear” part. Next, select the direction of motion and estimate how far you need to move. If a collision with a wall occurs in the direction of travel, then we move in the opposite direction. Retreat as long as there is a danger of hitting the projectile. When checking for shells, walls are counted. Thus, the projectile, which is guaranteed to fall into the wall - is ignored.
Regardless of the mode, adjust the angle of the hull so that it is perpendicular to the line of fire (the line connecting the centers of the tanks).
Program code and detailed description of the action algorithm
General view of the program code:

At the preliminary stage of the analysis of the initial data (before the main cycle is completed), the destroyed walls and their projectiles are screened out. The following is a choice of strategy. If you are in a danger zone, then
no checks are already done

If the enemy has disappeared behind the wall, then we will not return to safe mode, since the rotation of the tower to the nearest wall and back takes time, and an extra waste of time in combat conditions is unacceptable.
If the zone is safe, then we perform two checks:
1. The number of walls between the tank and the enemy;
2. The number of walls between the tank and each of the shells.

Testing shells must be performed because the enemy can hide behind the wall and shoot the corners of the tank. Waiting for the enemy to leave the wall in this case becomes meaningless.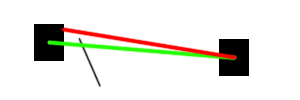

One wall is chosen for security reasons: if there are few “shields” left, then you must turn the tower on the enemy in advance to save time. Checking the walls between the tank and the enemy is shown below and uses the same function as checking the walls between the tank and the projectile (only different ends of the segments).

The function of searching for the number of “shields” is described below.
Projectiles are looped through, but the projectile hazard check is conducted at the point of impact, and not at the center of the hull. Reason: "tricky" enemy shooting from around the corner.

To simplify the calculations, the tank is considered as a circle described around the hull. The point of contact is taken at the point of intersection of the trajectory line of the projectile and perpendicular from the center of the tank to this line. In addition, the origin is transferred to the center of the tank.
For the straight line Ax + By + C = 0, the point of the perpendicular from the origin is calculated by the formulas:
x0 = - AC / (A ^ 2 + B ^ 2)
y0 = - BC / (A ^ 2 + B ^ 2)
Since the origin of coordinates in the center of the tank, then to check the hit it is necessary to calculate the length of the segment [(0,0) (x0, y0)]. If the length is less than the "radius" of the tank, then the projectile is dangerous.
Then calculate the distance that you need to roll back when maneuvering from the projectile (it will be needed later).
Next is determined by the area of contact: the front / rear of the tank. To do this, calculate the angle at which the straight line ((0,0) (x0, y0)) is located relative to the axis 0x. To simplify calculations (similar angles will be required in the future) are used.
segments dx, dy.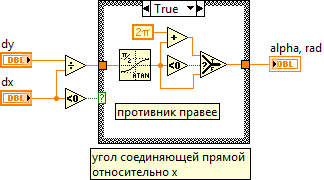
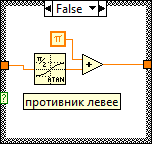


If the angle between this straight line and the direction of movement of the tank is less than pi / 2, then hit the front, otherwise - in the rear.
The last check that needs to be done is whether the projectile is flying into our tank. The first version of the tank did not take into account the direction of flight, and the tank tried to escape from the safe projectiles.
The check is performed as follows: since the projectile is specified by the beginning and length of the vector (componentwise), this allows to calculate the distance from the beginning of the vector to the center of the tank and from the end of the vector to the center of the tank. If the end of the vector is closer to the tank, then the projectile is flying in our direction.
The components of the vector are calculated as the difference of the coordinates of two points. The length of the vector is calculated by the Pythagorean theorem.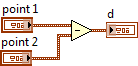



Next, it is checked how many wallboards there are. Verification is carried out on all shells, including safe projectiles.
Each wall is a segment. Another segment is constructed between the center of the hull or the point of impact and the center of the enemy or projectile. Further, it is checked whether these segments intersect. The verification algorithm is taken from the article at the following link: grafika.me/node/237 . Its essence lies in the analysis of vector products of vectors connecting different ends of segments.

Vector product in components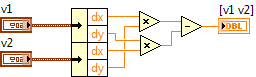

All walls are checked in a cycle, the first dangerous projectile is considered a breakpoint: since the situation is already dangerous, there is no sense in checking further. Thus, if less than two walls remain before the enemy, or a shell (not covered by walls) flies into the tank, then it is necessary to attack, otherwise destruction of the nearest walls for future maneuver continues.
Wall attack (safe mode)

First, the angle of rotation of the body is corrected. Then the angle of the “tank-enemy” straight line is determined with the x axis, using the functions of finding the vector and its angle with the Ox axis already described.

Determination of the angle of the body turn is as follows:

From the two corners the smallest one is chosen, since the “right-left” is not important here.

It is worth noting that, as in the case of shooting, the system (arbiter program) indicates the desired action: turn at once to the whole angle, make a shot. Then the system performs the permissible part of the desired: permissible rotation, shot (if the gun was reloaded).
In parallel, the distance from the center of the tank to all walls is calculated and the smallest value is selected.

After selecting a wall, its center is determined, where the shooting will take place. It should be noted that there may be several minima, but the system will issue the first in order. After the destruction of one wall (green direction), the next nearest one is selected. In theory, it may be blue (suppose that the distances are equal), but the next in order may be the far wall (red line), and the tower will turn for a long time to it, with several shots going to other walls. If you wish, you can modify the choice so that the nearest to the cannon is selected from the nearest walls.
closest to the gun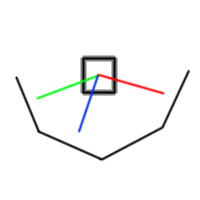

The distance to the wall is the distance from the point (center of the tank) to the segment. It should be borne in mind that sometimes the nearest point will be the point of intersection of a given segment by a perpendicular, and sometimes one of the ends of the segment.
We use the scalar product of vectors, the sign of which gives information about the directionality of the vectors (the entire algorithm is written in the code commentary).

Dot product of vectors

Further, the angle between the axis Ox and the connecting segment is determined (only the others are segments), and then the angle of rotation of the tower is calculated:

Further, it is checked where the turn is closer: clockwise or counterclockwise.
Enemy tank attack algorithm
The angles of rotation of the hull and the tower are calculated by the previously described methods. Further, the first dangerous projectile is located and the “best” side is maneuvered taking into account the point of impact of the projectile. However, it is necessary to verify that there are no obstacles to the retreat. If there are no dangerous projectiles, we rotate the body.
Check the path of retreat for the presence / absence of obstacles
The distance to travel was calculated when checking the danger of the projectile. We denote the current position of the tank black, and the final position gray. Thus, a rectangle is obtained, the side faces of which are the side faces of the tank hull, and the front faces are the current and desired position of the front part of the hull (blue frame). It is necessary to determine if this rectangle intersects any of the segments that define walls.

To determine the intersection, the Cohen-Sutherland algorithm is used, the description of which can be found in this link: ru.wikipedia.org/ Cohen's algorithm_ — Sutherland). To simplify the task, perform the following actions:
- rotation of the coordinate axis so that the forward motion is along the x axis
- transfer of the origin to the front of the tank.
Thus, the rectangle, the verification of which must be done:
- horizontal segments y = + - s / 2 (half the width of the tank);
- vertical: x = 0, x = godist (the distance that you need to go).
Next, you need to rotate and move all the segments of the wall when checking. Each wall is checked separately.

Now the position of the “right”, “left”, “above”, “below” points relative to the rectangle is determined by comparing the components x and y separately with the borders of the rectangle.

If an intersection has been found, the check is completed and it is impossible to move in this direction, and for exactly the chosen speed sign we give “full throttle”.
Conclusion
The proposed program code does not claim to be optimal due to the fact that the development, testing and debugging process took a short time. It should also be noted that some of the algorithms were taken from the head, some from the Internet and the team in no way encroaches on the authorship of the algorithms used. In the process of battles, the tank sometimes behaved not quite according to the algorithm - it “stuck” to the wall. Despite this, the intelligent tank control system from the LabVIEWPortal team proved to be the best and took the first place in the Olympiad. Playlist with video of the main fights of the tournament can be viewed at: www.youtube.com/playlist?list=PLKDkvzW_BvvH36vPdeiGKRvmhcZrjMseD
Thank you for your interest, we will be glad to hear your feedback.
Source: https://habr.com/ru/post/260289/
All Articles