As I drove Baldu-2, or in search of the optimal algorithm
Baldology, as it turned out (you heard about the existence of such a science, right?), Has a reflection on Habré in the form of several articles, here they are:
“Algorithm of quick word search in the game of noodle”
"Algorithm and tactics of finding words in the game Balda"
“How I drove Balda on Visual Basic for Applications for MS Access”
This article is a continuation of my previous, last in the list. The starting points for writing were the comments sent to me to the method of storing the dictionary in the form of a tree (Wikipedia article describing the Trie algorithm ), and also mentioning a chibiryaev colleague about his own search implementation, which spends finding a word in a 110,000-word dictionary 16 milliseconds!
')
Actually, task number 1 is to increase the speed of searching for words in a text array.
Let's start with the implementation of the algorithm Trie. To do this, we need to put the entire dictionary of nouns (43,303 words) into the structure of the related tree. Visual Basic does not support reference variables, like C ++ or C # (not to mention Pascal), but in this capacity array indices are fine.
Each element of the array should store the following information:
- Letter,
- The index of the element of the array, which begins with the letters that follow this letter in real words,
- The number of elements in this list of continuation letters,
- A sign of whether we will get a complete vocabulary word if we stop at the current letter.
In the picture it looks like this

The array must contain three data types - a letter, a logical value and a numeric value. An attempt to make it universal for Visual Basic with the Variant type, when an array element can be anything - even an object, did not lead to anything good - as a result, 4 arrays of the same length were declared, each of the required type, which added an essential 25% to the speed of work.
The filling of such an array occurs, of course, with the help of a recursive function. For her, interestingly, a search mechanism in the array of strings is also needed))) Exiting this vicious circle sheds light on one interesting programmer technology called “promotion”. Its essence is as follows.
Such a complex program as an optimizing compiler from C ++, for example, is best written ... in C ++. Well, not on the assembler! Where can we get such a compiler, if we only want to create it? The answer is - you need to take any, the most primitive, non-optimizing, written almost on the knee, just to work without errors. Then we run our source code through it, and we get a compiler program at the output - slow, like Windows NT 3.51, but already able to optimize and everything else that we have laid into it. But after feeding it our source code again, we will find the desired in all its glory. Another way is to write a full-fledged compiler on a certain simple subset C, for which to make again the most primitive code generator, and then as above. ( Wikipedia article on this topic )
Therefore, to create and fill the dictionary tree, I used a search algorithm through a 2-letter index from a previous version of my program.
I wanted to compare the result with the previous one - when the search was carried out using a 2-letter index. It turned out that the winnings are quite small, about 7 percent. The cardinal difference is only in the way the source dictionary is stored.
But I managed to speed up this algorithm by more than three times.
I have long deduced for myself that in programming there exists, by analogy with physics, something like the “rule of leverage”. In physics, it sounds like "We win in strength - we lose in the distance." In programming - “We win in speed, we lose in the amount of necessary memory”.
On an example: there are 2 ways to enter a multiplication operation into a computer. Either implement it in the form of an algorithm, or compose an array of all possible pairs of numbers with their works, and when prompted, select a ready-made result directly from the table. By the way, the school is taught to multiply using both of these methods. First, we memorize the multiplication table for numbers from 1 to 9, and then use the memorized results to multiply any numbers using the in-column algorithm.
I am distracted here from the physical ability to memorize all pairs of numbers with their works. In addition, there are intermediate options - something to predict and save, and then use to speed up the execution of the algorithm. The most striking example of this kind is the famous error in the Intel Pentium processor. To implement the fast division algorithm, a search table with a length of 1024 bytes was used, which the careless employee filled in incorrectly. The error cost the corporation almost half a billion dollars - Intel had to replace all the processors with an error, and this is in 1994 prices!
If we try to apply the lever rule (named after me) now, then where is the bottleneck of the search in the tree? When finding the necessary continuation letter among the elements by reference from the current letter. To avoid this search, let us store in the array not only those letters that are present in real words, but all 32, marking simply that some of them are not found in words. This will allow us to immediately move to the desired element of the array, simply calculating its index from the letter. This structure is naturally called the “sparse tree”. The size of the array, it must be said, will grow quite significantly - if a regular tree occupied 169,693 elements, then a sparse one — already 5,430,177 (although it is enough to store 2 values in each element of the corresponding sparse array, not 4 — the letter itself is not needed). it is determined by the place in the alphabet, and also the number of elements by reference is always 32).

Here is the corresponding picture - notice how the index number has increased for the same words (columns (X) for clarification, they are not in the array - not needed):

Well, the most extreme case when the answer about the belonging of a word to a dictionary is given in one command. Let all words of a certain length be stored in a logical array of the corresponding dimension, as in the picture for 2-letter words.
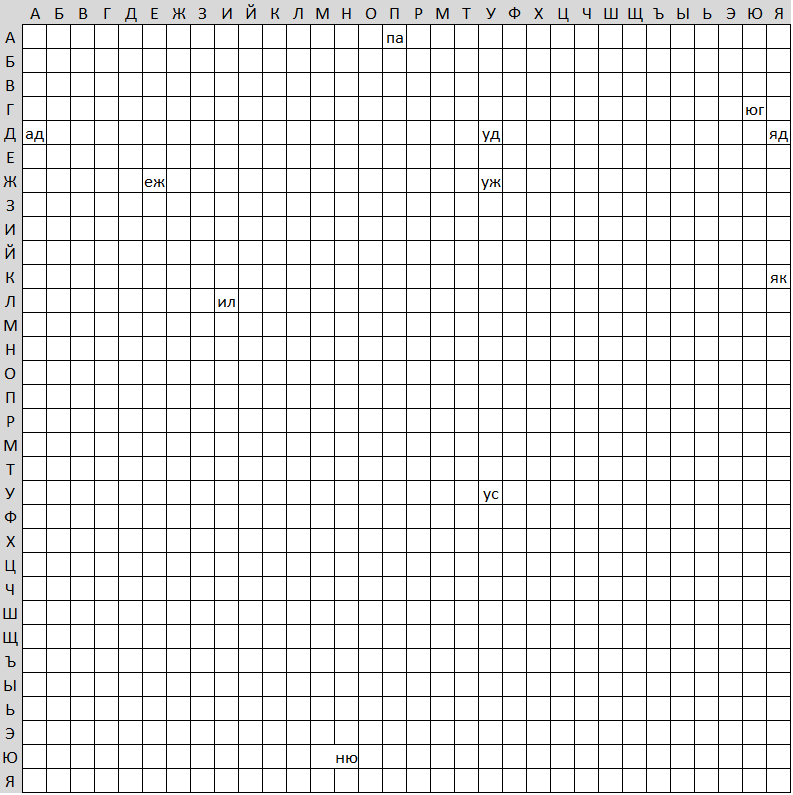
Here we just need to look at the value of the array element.
DICTIONARY ('B', 'A', 'L', 'D', 'A') = TRUE
DICTIONARY ('', '', '', '') = FALSE
(the latter is outrageous!)
The memory consumption at the same time (monstrous) is calculated slightly lower.
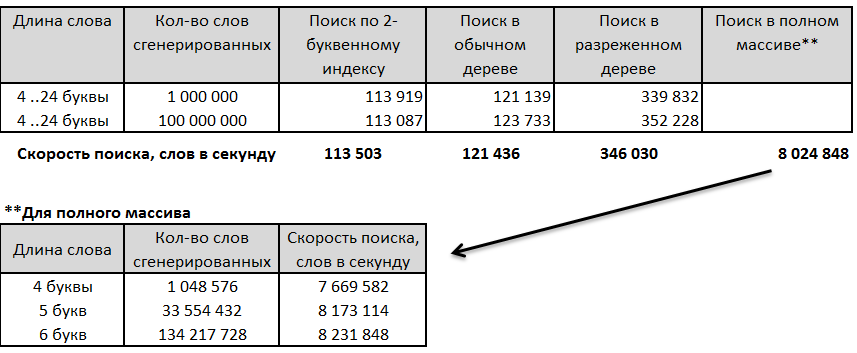
So, the comparison of 4 algorithms on words of different lengths. First, a million, and then one hundred million random words were generated, ranging in length from 4 to 24 letters, after which the search time was estimated.
1. Search by 2-letter index.
2. Search in ordinary tree
3. Search by sparse tree
4. Direct search in the array (due to restrictions on the size of the arrays is possible only for words no longer than 6 letters, and even then - 6 letters with reservations). But how fast!
(I need to mention the computer on which I thought it was Intel Core i3 -2125 at a frequency of 3.3GHz, 4GB RAM. The processor is 4-core, but this, I suspect, is unimportant, since the task is unparalleled, except that the OS itself and other processes are on other cores and do not interfere with our account.)
Small Offtopic - list of the longest nouns
22 AIR DEFINABILITY
22 NON-DISCIPLINE
22 UNDERESTATIVITY
22 FAILURE
22 GENERAL DISTRIBUTION
22 SELF-IMPROVEMENT
23 REVISION
24 HIGH ADVANTAGE
24 HUMAN CONSISTENCY
Not surprisingly, the longest words are mostly compound. By the way, there is a very elegant theory that the number of words in a language is, generally speaking, infinite. Since there is a rather big list of initial roots and the rules for the formation of new words from them (remember at least the derivatives of what the English call f-word). This theory, of course, is more understandable and gracious to programmers with their familiarity with recursion, than by philologists themselves! But I also stick to it. At one time I even collected these newly formed words:
- "he had the appearance of a freshly upset cat" (where is it from ??)
- “Soviet-elephant-coast-Kosty negotiations took place in Moscow” (from the collection of blunders of announcers of the Central Television of the USSR. The mentioned country - the Ivory Coast - is now called Cote d'Ivoire, which is the same, only in French)
- “I am treating tobacco smoking” (on the fence)
The last word formation amused me especially. It is possible, following this path, to come up with many new words. "Vodkopite", for example. Or "devogkoulie"))
By the way, even being the bearer of this very great and mighty Russian language, it is not always possible to understand whether the invented word is in front of us or not. For example, in Zaliznyak's dictionary there is the word “navigation”, which seems to me to be even more artificial than the “smoking” that is absent there! And what about “baldology”? In general, the tilled field.
It is interesting to look at the described algorithms in this section. The rule of the lever in physics is very concrete - the product of force and distance, which is a physical quantity, called work, invariably. You want to lift twice heavier load - use the lever 2 times longer, and you will manage with the same effort. Let's try to calculate how the memory spent on storing all these arrays compares with the gain in speed.
There is some dilemma. For the sake of speed, data storage in a computer is organized in a very non-compact form. The processor works the fastest with double words 4 bytes long (or even with quadruple words - 8 bytes?). Therefore, all compilers store data is very uneconomical. One bit (boolean) is enough for us to store the sign of a word in the dictionary, but in memory it will be a double word. (Attraction of unprecedented generosity! Ask the operating system for 1 bit of memory and get another 31 completely free! Users of privileged 64-bit systems will receive as much as 63 bits!)
But, probably, for the purity of counting, it is necessary to take the actual number of bits we need - the theoretical efficiency of the algorithm is abstract, that is, before the concrete implementation in the processor of this or that architecture (although this implementation can significantly - literally times! - change the speed when this algorithm).
By the way, we did not include in the calculation the simplest option - direct search. But it is many times slower and will bring us the whole picture, besides, this is not an algorithm at all, but a brute force method.

As you can see, the increase in the speed of the search is given with each step to us with more and moreblood .
By the way, it is interesting to assess the quality of a random (pseudo-random, of course) number generator included in VBA (in fact, in Windows itself). When we generate some fairly large number of character strings, it must also contain real vocabulary nouns (remember the saying about monkeys that type on typewriters and do so until one of them has Shakespeare's complete works / Leo Tolstoy / Eduard Limonov?)
Since we were limited to only a hundred million words generated (just something! But I wanted to publish this article during my lifetime), we can check the quality of the generator only with words of up to 6 letters, since we’ve never been able to use words longer than as it turned out, do not stumble. But even in these figures, the system demonstrates elegant quality! Here is the result

The most characteristic is the first line. It shows the difference from the theoretical maximum of only 3 hundredths of a percent !!! That is, we should even more words, the accuracy of entering the dictionary would be even higher.
Well, and for sweet. In the first comment to the last article, a colleague zorgzerg threatened to kill me, since I deprived people of the game buzz live, arming myself and others with a tool for dishonest play (plus, however, set)))). I have to say the following. Balda refers to mathematical problems that are completely calculated on a completely average modern computer. In fact, chess can already be attributed to such tasks (after the supercomputer wins the world champion Garry Kasparov), but there the system was more powerful, and the team of programmers ... a little better. Therefore, we, humans, should devote ourselves to much more complex and difficult to formalize tasks, and let computers have fun with themselves, under our supervision and to our joy. For example: using the latest “sparse tree” algorithm, I forced the computer, playing for both sides, to drive away 3,264 batches (according to the number of 5-letter words in the dictionary used to start the game). At every step, my iron horse chose the longest word found — the first from the list, the last from the list, the random from the list (if there were several such words). The usual average game that a person, that computer, brings each side from 50 to 60 points (the sum of the lengths of the words found), that is, there are mostly 5-letter words, well, very rarely 6-letter or higher. But the computer came across some much more interesting options - and the total bill sometimes went off scale for 150!
Rate, baldists! How often did you have to knock out your opponent with a chic 11-letter word? And my computer did it!

“Algorithm of quick word search in the game of noodle”
"Algorithm and tactics of finding words in the game Balda"
“How I drove Balda on Visual Basic for Applications for MS Access”
This article is a continuation of my previous, last in the list. The starting points for writing were the comments sent to me to the method of storing the dictionary in the form of a tree (Wikipedia article describing the Trie algorithm ), and also mentioning a chibiryaev colleague about his own search implementation, which spends finding a word in a 110,000-word dictionary 16 milliseconds!
')
Actually, task number 1 is to increase the speed of searching for words in a text array.
Let's start with the implementation of the algorithm Trie. To do this, we need to put the entire dictionary of nouns (43,303 words) into the structure of the related tree. Visual Basic does not support reference variables, like C ++ or C # (not to mention Pascal), but in this capacity array indices are fine.
Each element of the array should store the following information:
- Letter,
- The index of the element of the array, which begins with the letters that follow this letter in real words,
- The number of elements in this list of continuation letters,
- A sign of whether we will get a complete vocabulary word if we stop at the current letter.
In the picture it looks like this

The array must contain three data types - a letter, a logical value and a numeric value. An attempt to make it universal for Visual Basic with the Variant type, when an array element can be anything - even an object, did not lead to anything good - as a result, 4 arrays of the same length were declared, each of the required type, which added an essential 25% to the speed of work.
The filling of such an array occurs, of course, with the help of a recursive function. For her, interestingly, a search mechanism in the array of strings is also needed))) Exiting this vicious circle sheds light on one interesting programmer technology called “promotion”. Its essence is as follows.
Such a complex program as an optimizing compiler from C ++, for example, is best written ... in C ++. Well, not on the assembler! Where can we get such a compiler, if we only want to create it? The answer is - you need to take any, the most primitive, non-optimizing, written almost on the knee, just to work without errors. Then we run our source code through it, and we get a compiler program at the output - slow, like Windows NT 3.51, but already able to optimize and everything else that we have laid into it. But after feeding it our source code again, we will find the desired in all its glory. Another way is to write a full-fledged compiler on a certain simple subset C, for which to make again the most primitive code generator, and then as above. ( Wikipedia article on this topic )
Therefore, to create and fill the dictionary tree, I used a search algorithm through a 2-letter index from a previous version of my program.
I wanted to compare the result with the previous one - when the search was carried out using a 2-letter index. It turned out that the winnings are quite small, about 7 percent. The cardinal difference is only in the way the source dictionary is stored.
But I managed to speed up this algorithm by more than three times.
I have long deduced for myself that in programming there exists, by analogy with physics, something like the “rule of leverage”. In physics, it sounds like "We win in strength - we lose in the distance." In programming - “We win in speed, we lose in the amount of necessary memory”.
On an example: there are 2 ways to enter a multiplication operation into a computer. Either implement it in the form of an algorithm, or compose an array of all possible pairs of numbers with their works, and when prompted, select a ready-made result directly from the table. By the way, the school is taught to multiply using both of these methods. First, we memorize the multiplication table for numbers from 1 to 9, and then use the memorized results to multiply any numbers using the in-column algorithm.
I am distracted here from the physical ability to memorize all pairs of numbers with their works. In addition, there are intermediate options - something to predict and save, and then use to speed up the execution of the algorithm. The most striking example of this kind is the famous error in the Intel Pentium processor. To implement the fast division algorithm, a search table with a length of 1024 bytes was used, which the careless employee filled in incorrectly. The error cost the corporation almost half a billion dollars - Intel had to replace all the processors with an error, and this is in 1994 prices!
If we try to apply the lever rule (named after me) now, then where is the bottleneck of the search in the tree? When finding the necessary continuation letter among the elements by reference from the current letter. To avoid this search, let us store in the array not only those letters that are present in real words, but all 32, marking simply that some of them are not found in words. This will allow us to immediately move to the desired element of the array, simply calculating its index from the letter. This structure is naturally called the “sparse tree”. The size of the array, it must be said, will grow quite significantly - if a regular tree occupied 169,693 elements, then a sparse one — already 5,430,177 (although it is enough to store 2 values in each element of the corresponding sparse array, not 4 — the letter itself is not needed). it is determined by the place in the alphabet, and also the number of elements by reference is always 32).

Here is the corresponding picture - notice how the index number has increased for the same words (columns (X) for clarification, they are not in the array - not needed):

Well, the most extreme case when the answer about the belonging of a word to a dictionary is given in one command. Let all words of a certain length be stored in a logical array of the corresponding dimension, as in the picture for 2-letter words.

Here we just need to look at the value of the array element.
DICTIONARY ('B', 'A', 'L', 'D', 'A') = TRUE
DICTIONARY ('', '', '', '') = FALSE
(the latter is outrageous!)
The memory consumption at the same time (monstrous) is calculated slightly lower.
So, the comparison of 4 algorithms on words of different lengths. First, a million, and then one hundred million random words were generated, ranging in length from 4 to 24 letters, after which the search time was estimated.
1. Search by 2-letter index.
2. Search in ordinary tree
3. Search by sparse tree
4. Direct search in the array (due to restrictions on the size of the arrays is possible only for words no longer than 6 letters, and even then - 6 letters with reservations). But how fast!

(I need to mention the computer on which I thought it was Intel Core i3 -2125 at a frequency of 3.3GHz, 4GB RAM. The processor is 4-core, but this, I suspect, is unimportant, since the task is unparalleled, except that the OS itself and other processes are on other cores and do not interfere with our account.)
Small Offtopic - list of the longest nouns
22 AIR DEFINABILITY
22 NON-DISCIPLINE
22 UNDERESTATIVITY
22 FAILURE
22 GENERAL DISTRIBUTION
22 SELF-IMPROVEMENT
23 REVISION
24 HIGH ADVANTAGE
24 HUMAN CONSISTENCY
Not surprisingly, the longest words are mostly compound. By the way, there is a very elegant theory that the number of words in a language is, generally speaking, infinite. Since there is a rather big list of initial roots and the rules for the formation of new words from them (remember at least the derivatives of what the English call f-word). This theory, of course, is more understandable and gracious to programmers with their familiarity with recursion, than by philologists themselves! But I also stick to it. At one time I even collected these newly formed words:
- "he had the appearance of a freshly upset cat" (where is it from ??)
- “Soviet-elephant-coast-Kosty negotiations took place in Moscow” (from the collection of blunders of announcers of the Central Television of the USSR. The mentioned country - the Ivory Coast - is now called Cote d'Ivoire, which is the same, only in French)
- “I am treating tobacco smoking” (on the fence)
The last word formation amused me especially. It is possible, following this path, to come up with many new words. "Vodkopite", for example. Or "devogkoulie"))
By the way, even being the bearer of this very great and mighty Russian language, it is not always possible to understand whether the invented word is in front of us or not. For example, in Zaliznyak's dictionary there is the word “navigation”, which seems to me to be even more artificial than the “smoking” that is absent there! And what about “baldology”? In general, the tilled field.
It is interesting to look at the described algorithms in this section. The rule of the lever in physics is very concrete - the product of force and distance, which is a physical quantity, called work, invariably. You want to lift twice heavier load - use the lever 2 times longer, and you will manage with the same effort. Let's try to calculate how the memory spent on storing all these arrays compares with the gain in speed.
There is some dilemma. For the sake of speed, data storage in a computer is organized in a very non-compact form. The processor works the fastest with double words 4 bytes long (or even with quadruple words - 8 bytes?). Therefore, all compilers store data is very uneconomical. One bit (boolean) is enough for us to store the sign of a word in the dictionary, but in memory it will be a double word. (Attraction of unprecedented generosity! Ask the operating system for 1 bit of memory and get another 31 completely free! Users of privileged 64-bit systems will receive as much as 63 bits!)
But, probably, for the purity of counting, it is necessary to take the actual number of bits we need - the theoretical efficiency of the algorithm is abstract, that is, before the concrete implementation in the processor of this or that architecture (although this implementation can significantly - literally times! - change the speed when this algorithm).
By the way, we did not include in the calculation the simplest option - direct search. But it is many times slower and will bring us the whole picture, besides, this is not an algorithm at all, but a brute force method.

As you can see, the increase in the speed of the search is given with each step to us with more and more
By the way, it is interesting to assess the quality of a random (pseudo-random, of course) number generator included in VBA (in fact, in Windows itself). When we generate some fairly large number of character strings, it must also contain real vocabulary nouns (remember the saying about monkeys that type on typewriters and do so until one of them has Shakespeare's complete works / Leo Tolstoy / Eduard Limonov?)
Since we were limited to only a hundred million words generated (just something! But I wanted to publish this article during my lifetime), we can check the quality of the generator only with words of up to 6 letters, since we’ve never been able to use words longer than as it turned out, do not stumble. But even in these figures, the system demonstrates elegant quality! Here is the result

The most characteristic is the first line. It shows the difference from the theoretical maximum of only 3 hundredths of a percent !!! That is, we should even more words, the accuracy of entering the dictionary would be even higher.
Well, and for sweet. In the first comment to the last article, a colleague zorgzerg threatened to kill me, since I deprived people of the game buzz live, arming myself and others with a tool for dishonest play (plus, however, set)))). I have to say the following. Balda refers to mathematical problems that are completely calculated on a completely average modern computer. In fact, chess can already be attributed to such tasks (after the supercomputer wins the world champion Garry Kasparov), but there the system was more powerful, and the team of programmers ... a little better. Therefore, we, humans, should devote ourselves to much more complex and difficult to formalize tasks, and let computers have fun with themselves, under our supervision and to our joy. For example: using the latest “sparse tree” algorithm, I forced the computer, playing for both sides, to drive away 3,264 batches (according to the number of 5-letter words in the dictionary used to start the game). At every step, my iron horse chose the longest word found — the first from the list, the last from the list, the random from the list (if there were several such words). The usual average game that a person, that computer, brings each side from 50 to 60 points (the sum of the lengths of the words found), that is, there are mostly 5-letter words, well, very rarely 6-letter or higher. But the computer came across some much more interesting options - and the total bill sometimes went off scale for 150!
Rate, baldists! How often did you have to knock out your opponent with a chic 11-letter word? And my computer did it!

Source: https://habr.com/ru/post/259501/
All Articles