100 Years Later: Ramanujan Records Complete

Translation of Oleg Marichev and Michael Trott's post " After 100 Years, Ramanujan Gap Filled ".
Download the file containing the text of the article, interactive models and all the code given in the article here .
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

A hundred years ago, Srinivasa Ramanujan and G.H. Hardy began a famous correspondence about such amazing things in mathematics that Hardy described it as something hardly possible to believe in it. On May 1, 1913, Ramanujan received a permanent position at the University of Cambridge. After five years and one day, he became a researcher at the Royal Society, and his group became the most prestigious at that time scientific group in the world. In 1919, Ramanujan became fatally ill during a long journey on the steamer Nagoya to India, which took place from February 27th to March 13th. All he had was a notebook and a pen (yes, no Mathematica at the time), and before his death he wanted to leave his equations on paper. He argued that he had solutions for a number of functions, but he only had time to write down a few before moving on to other areas of mathematics. He wrote down the following incomplete equation and 14 others (see below), of which only three are currently solved.



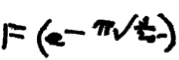
He died a few months, probably from liver amebiasis. His last notebook was sent by the University of Madras to G.H. Hardy, who then handed it to the mathematician G. N. Watson . In 1965, when Watson died, the college director found a notebook in his office, selecting documents for destruction. George Andrews re-opened this notebook in 1976, and finally, in 1987, it was published. Bruce Berndt and Andrews wrote about Ramanujan ’s lost Notebook in a series of books ( Part 1 , Part 2 , and Part 3 ). As Berndt said: “The discovery of this“ lost notebook ”caused a boom in the mathematical world just like the opening of Beethoven’s tenth symphony in the musical world.”

In his book, analyzing the results of Ramanujan, Berndt points out the existence of a solution for , however, notes that the decision is not particularly elegant, in order to bring it into it. As will be shown below, there is a solution as elegant as the rest found by Ramanujan himself.
')


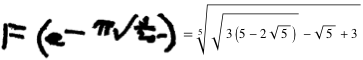
What does this equation mean? Let's start with a comparison of arithmetic and geometric progressions.

The sum of the first n members of some arithmetic progression: 1 + 2 + 3 + ... + n .

The sum of the first n members of a certain geometric progression: a ¹ + a ² + a ³ +… + a ⁿ .

For each type of progression, we can predict its behavior using the partial sum formula, if we reduce the above expressions to their closed form.

Here is another form of arithmetic progression presented in the form of continuous fractions :



where is the symbol corresponds to the ContinuedFractionK function in Mathematica .

Similarly, the “geometric” version of continuous fractions is known as the Rogers-Ramanujan R function . It is related to the Rogers-Ramanujan S function ( Leonard James Rogers published with Ramanujan in 1919). In the “lost notebook”, F ( q ) is represented as S ( q ).

R ( q ) is a continuous fraction of the following form:



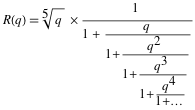
And similarly for S ( q ). (Using a multiplier makes the formulas more “comfortable”). Here are more formal definitions:





These functions are related by . Many published works mention S ( q ) = - R (- q ), but this is not true due to the multi-leaf root in the complex domain. We can also specify R and S through the Pohgammer q-symbols to significantly accelerate computations.





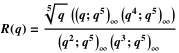
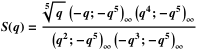
Here is an illustration of the behavior of the function R in the unit circle on the complex plane. The obtained values ​​can be complex, therefore the real, imaginary parts, the argument and the absolute value (Im, Re, Arg and Abs) of the function R ( q ) are displayed. The unit circle itself is the natural limit of the analyticity of this function and contains many features of the function R ( q ). As you can see, the Rogers-Ramanujan function is beautiful not only because of its mathematical properties, but also purely visual.



The functions R and S are two of the small number of named functions associated with continued fractions. Recently, we have collected theorems and formulas for the functions R and S , including those incomplete from Ramanujan’s “lost notebook”. The last line is equivalent .



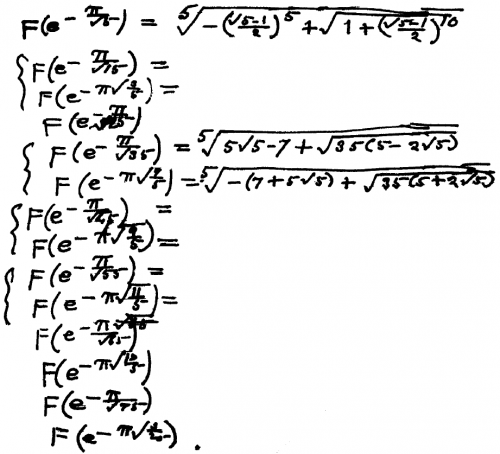
Many of them were re-found after Ramanujan. All of them are easily solved in Mathematica . Here are the well-known solutions, starting with those that appeared earlier, as well as those that Oleg Marichev first implemented in Mathematica .



Bruce Berndt noted: “meaning can be determined by value and the well-known equation relating R ( q ⁵ ) to R ( q ). We will not give the resulting value here, because it is not particularly elegant. "

With Simplify , RootReduce, and many other Mathematica functions, large equations can be reduced to their most elegant form. Ramanujan used chalk and his intellect to simplify the results obtained - he erased the cumbersome ones from his list and left the graceful ones. It seems likely that Ramanujan actually knew an elegant solution, or at least a way to find him, but he no longer had time to write it down. Here is the method we used. First, get a numerical value at the point of interest. Next, you should get some closed algebraic form for this number. Then express the resulting algebraic number through the construction of radicals. Then you need to check the resulting form numerically with the original value with very high accuracy.















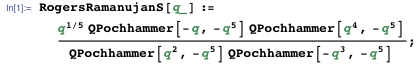
That is, we check that the numerical value of the proposed form is the same as the value of the function. The values ​​match at least in the first 10,000 digits.





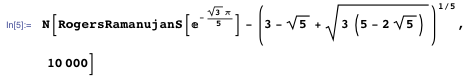
Since both of them are algebraic numbers of a very elegant form, this is a pretty convincing check. And the method can easily be generalized to search for many currently unknown values ​​of S ( q ) and R ( q ) .

Actual proof can be implemented through modular equations (modular equations). This is a 5th order modular equation for S :





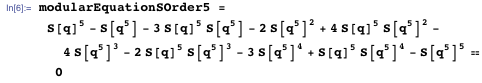
We use the previously known value. for S ( q ⁵ ) and solve the equation for S ( q ) to get the value .









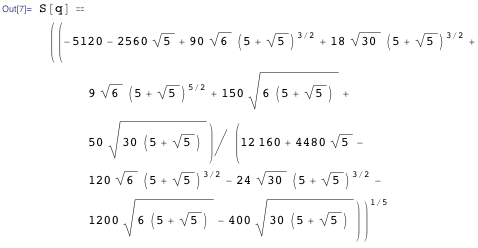
Having got rid of the denominators, we get the result below.





The Ramanujan equations are similar in scope to our recent work — the addition of many different knowledge of continued fractions in Wolfram | Alpha . In one of the following posts we will talk about new features, such as entering a query about a continued fraction K (1, n, {n, 1, inf}) .

We also compiled a list of hundreds of exact values ​​in the interactive demonstration “ Ramanujan R and S ”.



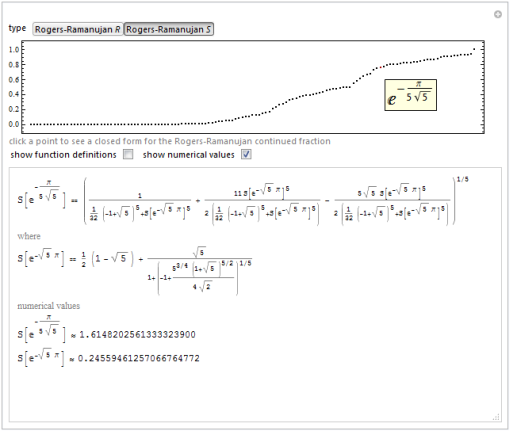
“Not very elegant” is something that cannot be said about the works of Ramanujan. And we were glad to show how elegant his ideas are.