Tunnel modeling - version 0.9

Good time to read, dear members habrahabr.ru



This post uses an attempt to enter measurement terms in a spherical coordinate system.



The concepts of abstractness, phase of activity, as well as groups and periods of complexity are introduced.

')

A graphical notation for modeling, based on the proposed allocation of groups of terms, is described.

1. Spherical worldview model

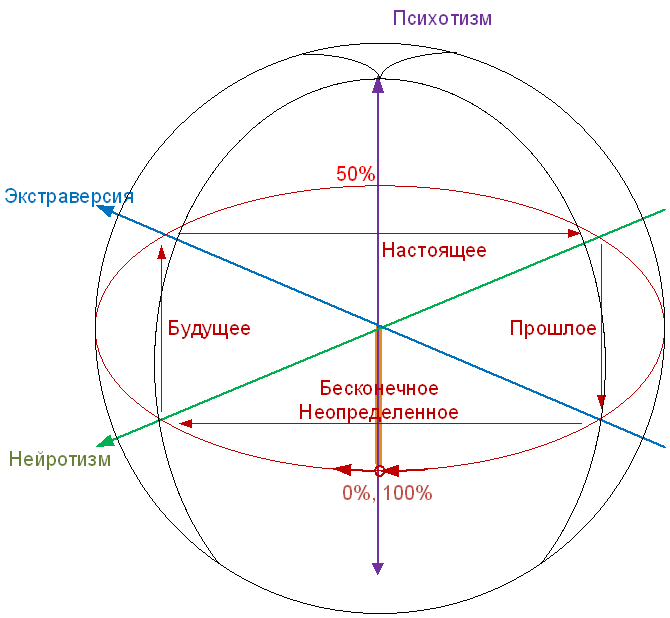
Hans Jürgen Aysenck has developed a coordinate system for measuring the psychological characteristics of a person, consisting of scales of extraversion, neuroticism and psychoticism.



These scales are used in psychological tests to determine the type of human temperament, as well as in tests to measure IQ



Such a measurement system can be considered a three-dimensional Cartesian coordinate system, and, therefore, it is possible to go from the Cartesian coordinates to the polar ones.

Fig. 1 Relationship Cartesian and polar coordinates



The resulting coordinate system in this article will not use the distance from the center of the coordinate system, but will use the angle between the point and the horizontal plane passing through the center (similar to latitude in geographic coordinates of the Earth), and the angle of projection on the horizontal plane (similar to longitude in geographical coordinates Earth).



For the resulting scales of spherical coordinates, we introduce the following

units:

• abstractness corresponding to longitude, expressed as a percentage, and taking a value of 0% for the lower pole, 100% for the upper pole, and 50% for a point located on a circle formed by the intersection of the sphere and the horizontal plane;
• phase corresponding to longitude, expressed as a percentage, increasing in a clockwise direction and taking a value of 0%, as well as 100% for a bisector between the positive direction of the axis of neuroticism and the negative direction of the axis of extraversion (introversion)

Let us turn this spherical coordinate system onto a plane, as was done when making the first maps of the Earth (cylindrical Mercator projection). In this case, the upper and lower poles become horizontal lines.







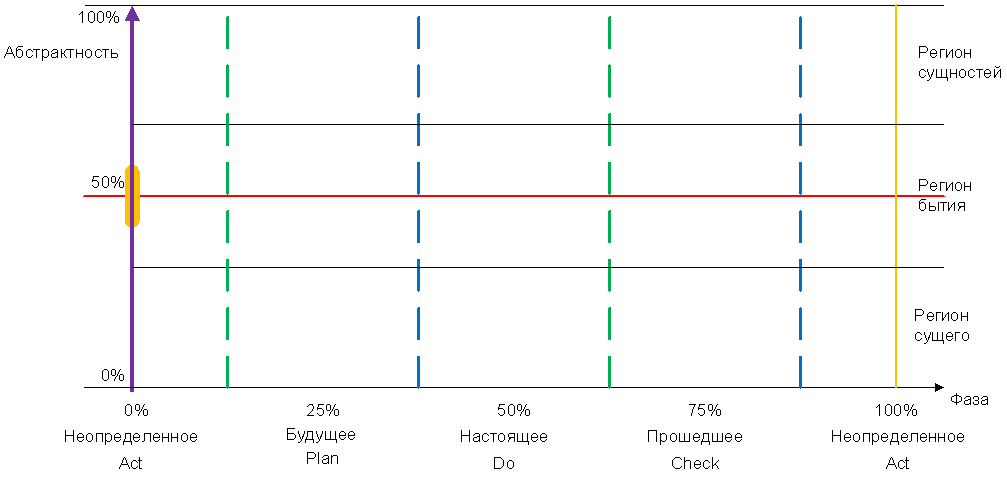
Fig. 2 Polar coordinates with selected regions



The author investigated the possibility of using the obtained coordinate system to determine the numerical values ​​of the terms of the domain modeling techniques, in particular, the widely used SADT and UML techniques, and positive results were obtained.

2. Periodic table of difficulty

As the list of analyzed terms expanded, a need emerged to highlight new horizontal levels on the abstract scale, in which the grouping by the type of sigmoid phases was revealed.







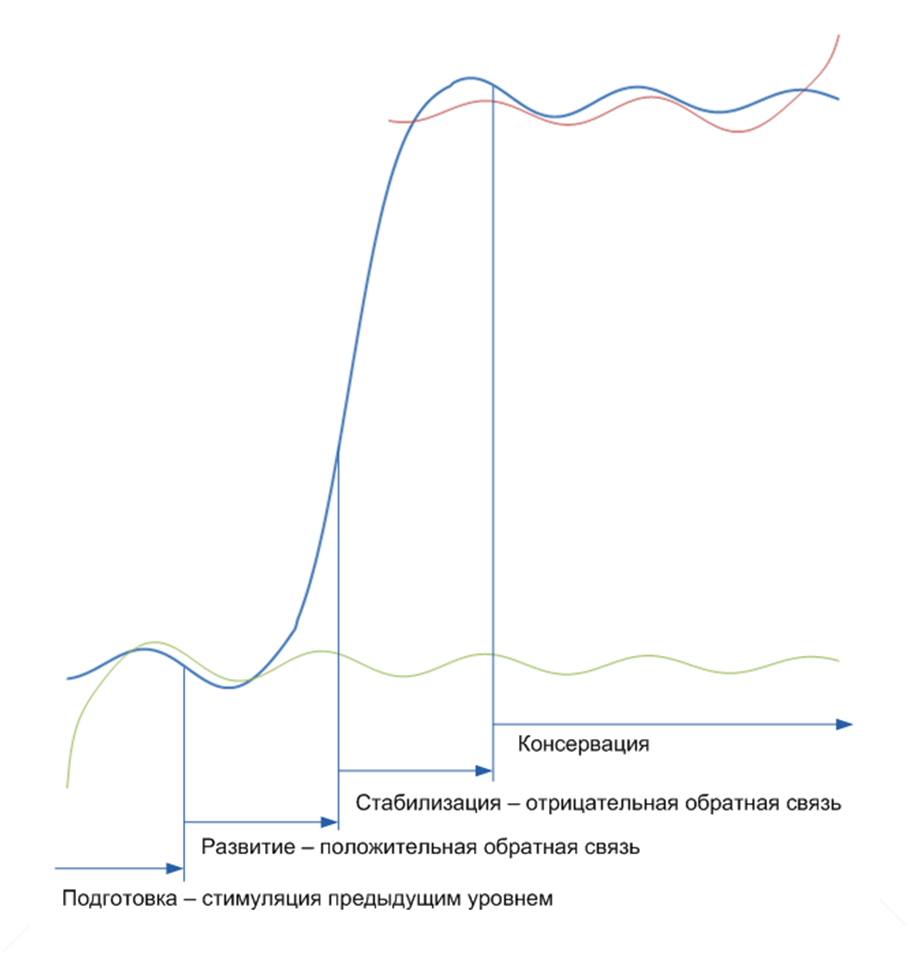
Fig. 3 Sigmoid chain complication



For certain elements of complication (by analogy with the periodic table of chemical elements of DI Mendeleev), the use of the terms complexity and the period of complexity is suggested.



The periods of difficulty are shown in Figure 3. Proposed

the following explanation for their selection:

1. preparatory stage is characterized by compensation needs
   
   disturbances from the previous level;
2. the developmental stage is associated with the emergence of positive feedback that stimulates development;
3. the stabilization stage is associated with the appearance of negative feedback that limits development;
4. - the conservation phase is characterized by a stable existence, and is not included in separate groups of terms.

At the moment, there are three groups of complexity of modeling terms. Complexity groups symmetrically spread from the upper and lower poles.



At the same time, the correspondence of groups and periods with subjects of university education is proposed (Table 1).

Table 1.

The proposed classification of educational subjects

Group	Period	Abstraction	Specific
Random	Stabilization	Logics	The quantum physics
Items	Training	Maths	Physics
	Development	Philosophy	Chemistry
	Stabilization	Cultural studies	Biology
Processes	Training	Political science	Psychology
	Development	Management	Sociology
	Stabilization	Marketing	Economy
Society	Training	Public relations	Synergetics
	Development	Quality control	Technology

For the period “development” of the group “random”, the terms future for abstract and past for concrete are suggested.

2. Graphic primitives of tunnel simulation

To display the level of complexity, a notation system is proposed, based on the labels on the left side of the rectangular modeling element. For designations, the use of pairs of triangles is proposed. Triangles in a pair can have a shaded and not shaded state, which allows the use of an analogue of a binary code.



To build block diagrams of programs, it is also necessary to have elements for branching and looping operations. These elements are shown in Figures 5 and 6.







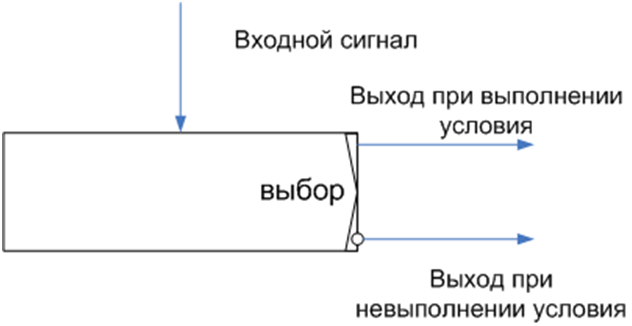
Figure 5 Modeling a choice of two alternatives







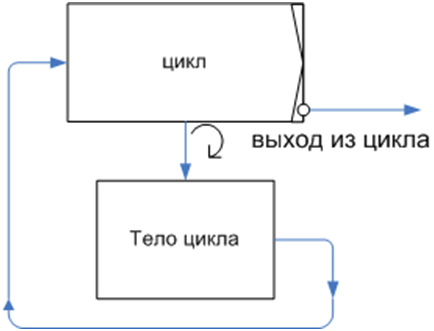
Figure 6. Cycle simulation



Phases corresponding to elements of the Deming-Schugart cycle -Act-Plan-Do-Check-

indicated by special characters on the right side of the element's rectangle

modeling.







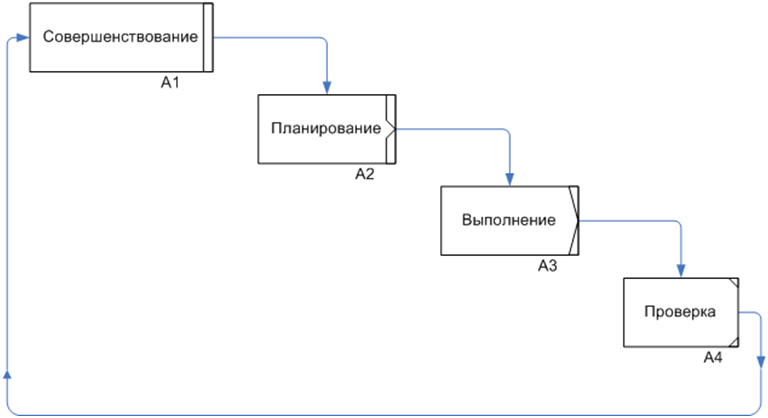
Figure 7. Elements of the Deming-Shewhart cycle



The main custom modeling element contains a menu that allows you to select the features of the image.







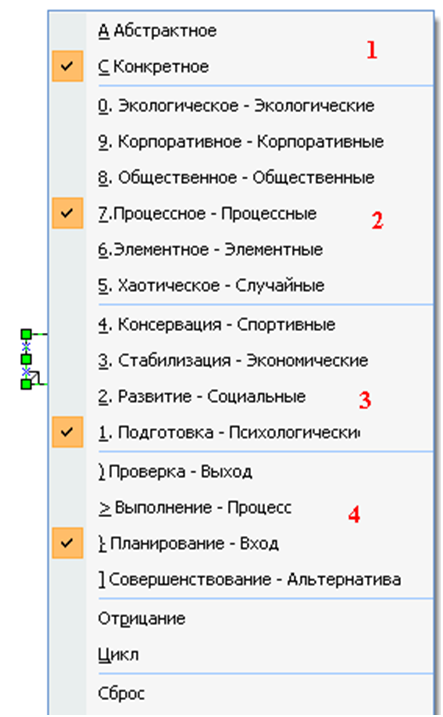
Fig. 8. Rectangle view customization menu



Refinement of the image is made by sequential refinement of the groups of menu items:

1. abstractness
2. difficulty group
3. period of difficulty
4. element of the Deming-Shewhart cycle

Hierarchical decomposition can be subjected to both rectangles and arrows







Fig. 9. Representation of decomposition arrows



The remaining elements can be borrowed from well-established modeling techniques - UML, SADT, BPMN, DRAGON, Archimate.

4. Proposal for the projection of being on the worldview

When considering a spherical model, a paradox arises between the complexity of the central region and the “lack of space” to reflect this complexity.



To explain this discrepancy, we can assume the hyperbolic dependence of complexity with distance from the poles.



An illustration of this view can serve as figure 10:

Figure 10. The projection of being on the sphere of outlook



In view of the promising areas, we can propose an extension of the Auguste Comte classification of sciences, taking into account the symmetric dualism of Rene Descartes









Figure 11. Proposal for a sequence of analysis



A brief reference to the elements of the notation is shown in Figure 12.





Figure 12. Designations for knowledge sections



Topics on Habrahabr:

Tunnel modeling - version 1.0

The ratio of abstraction and complexity in modeling

habrahabr.ru/post/254275

Modeling difficulty levels

habrahabr.ru/post/238599



Ideology presentation

habrahabr.ru/post/177131

Transformation approach Zachman

habrahabr.ru/post/267749



ISO 15926 vs Semantics: a comparative analysis of semantic models

habrahabr.ru/post/178973

Create a new OS. Really new, really operational, and the truth - the system

habrahabr.ru/company/intel/blog/300884



Literature:

ru.wikipedia.org/wiki/Teory_Functional_Systems

ru.wikipedia.org/wiki/Aisenk , _Hans_Jurgen

Karamyshev S.V. Where to take the S-curve?

www.metodolog.ru/01493/01493.html

Zharov A. Future. Evolution continues

fan.lib.ru/z/zharow_a/2050buduschee.shtml

Narinyani A.S. Between Knowledge and Ignorance - Naive Topography

viperson.ru/articles/aleksandr-narinyani-mezhdu-znaniem-i-neznaniem-naivnaya-topografiya

Diffusion of innovations in Wikipedia

ru.wikipedia.org/wiki/Diffusion of Innovations

Five-factor model of human personality

https://ru.wikipedia.org/wiki/Large_fine_(psychology)