The largest small polyhedra: new solutions in combinatorial geometry

Translation of the Ed Pegg Jr. post " Biggest Little Polyhedron — New Solutions in Combinatorial Geometry ".
Download the file containing the text of the article, interactive models of polyhedra and the code given in the article here .
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

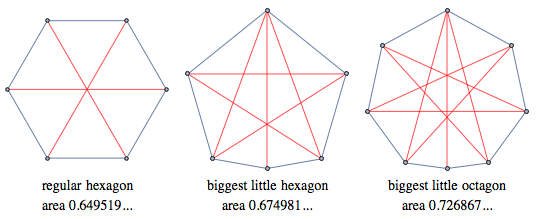
In many areas of mathematics, the answer is one . Raising a non-negative number to a square that is larger or smaller than one will give a greater or smaller number, respectively. Sometimes, in order to determine whether something is “large”, it is necessary to find out whether the largest size of this object is larger than one. For example, Saturn’s giant hexagon with a side length of 13,800 km could be classified as large. “Small polygon” is the one with the maximum distance between vertices equal to one . In 1975, Ron Graham discovered the largest small hexagon , which, as shown below, has a larger area than the regular hexagon. Red diagonals have a unit length. All other (non-connected) diagonals are shorter.



I always wondered what the largest small polyhedron would look like. In Mathematica 10, a new functional object, Volume [ ConvexHullMesh [points]] , was introduced, and I thought that this problem could be solved by selecting random points. Below is the code to select, calculate, and visualize a random small polyhedron. Scrolling this code thousands of times, you can get a good approximation in the best of results. Here, here I ran the code three times. One of the results is probably better than the rest.


')
The image below shows the best solutions that were obtained through randomly selected points. I put it in the Wolfram Community in the discussion of the largest small polyhedron (hereinafter - MMO) and received some useful comments from Robin Houston and Todd Roland. To find solutions, I decided to use the results of the Thompson task visualization . In the Thomson problem, electrons repel each other on a sphere. The 12 points repelling each other tend to the vertices of the icosahedron, which is not effective for HMMs, since the largest distances pass through the center of the sphere, as well as for regular hexagons in the two-dimensional case. I changed the code for the Thompson problem so that the points bounced off each other and from all opposite ones, and this gave quite good initial values.



For four points, the solution is a regular tetrahedron with a volume / 12 = 0.117851.

For five points, the solution will be an equilateral triangle with unit lengths of sides and a unit perpendicular to this triangle, and the volume will be equal to / 12 = 0.1443375; This decision was received in the 1976th year [1].



I will use the term 6-MMD to denote the greatest small polyhedron with six points. In 2003, the volume of 6-mm was calculated to four digits [2, 3]. Below are 6-mm and 7-mm, single diagonals are highlighted in red.



In order to find them myself, I first selected the best options from more than a thousand, and then used the simulated annealing algorithm (probabilistic task of finding a good approximation to the global optimum of this function in a wide search space - approx. Lane) to improve results. For each of the points of optimal solutions, I went through the space around these points to find the best solution, shifting them slightly. Then I reduced the search space even more, and so from time to time. Some of the solutions seemed to strive for mutual symmetry. For example, for seven points, the best solution aimed at this polyhedron with a value of r about half, which represents the relative size of the upper triangle 456.



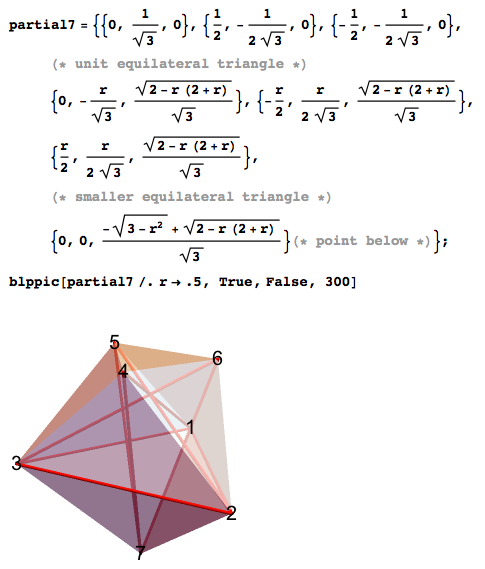
The exact volume can be obtained through the tetrahedron, which is determined through the points {{2,3,4,7}, {2,4,6,7}, {5,4,7,6}}, and the volume of the first two should be tripled from symmetry considerations. Look at the volumes of the tetrahedra, and replace any pair of numbers in the tetrahedron so that a negative volume is obtained.



After we change the ratio in the last tetrahedron, we can calculate the exact value of r , which will give the exact and optimal volume. We will use the same method for other cases.



The 16-mm MMC solution takes more than a minute, so I had to break it.



The first value in the solutions is the optimal volume, is the Root object, and the second is the optimal value of r . Here, this table will be more careful.



And this is far beyond what I could have done manually. Using a random sample of points, an annealing simulation algorithm, symmetry search, Solve [] and Maximize [], I was able to find the exact values ​​of the volumes of n-HMM (the largest small polyhedra) for n = 6, 7, 8, 9, and 16.

View 8-MMOs from several sides, where single diagonals are highlighted in red.



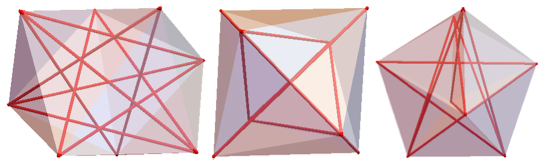
View 9-MMOs from several sides:



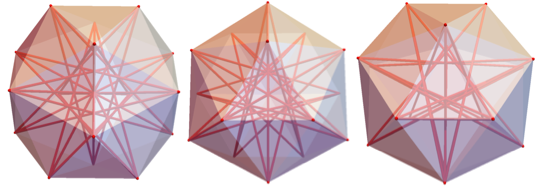
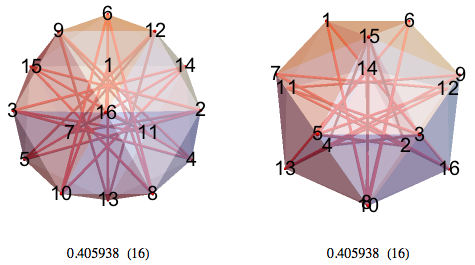
View of the 16-MMO from several sides:



The following 8-mm contains single perpendiculars 1-2 and 3-4 above and below the base, respectively. Below 9-NMM contains triangles △ 123, △ 456 and △ 789.



The 16-HMM given below is a truncated tetrahedron consisting of points 1-12 with additional points 13-16.



Pretty hard, isn't it? Using the method of selecting points on a sphere , random numbers in the intervals [–Pi; Pi] and [–1; 1] on the unit sphere, you can set a uniform distribution of points. Points on the unit sphere can be mapped back to points in the rectangle [–Pi; Pi] x [–1; one]. This is what happens for solutions 8,9,16-hmm.



For 10-hmm, I was not able to find the exact solution, but I can provide a numerical solution with any degree of accuracy. Contact me if you have any idea how to find the root object. In the executable version of this article on the Wolfram Language in the initialization section, you can find this very difficult expression.



There are two types of 10-mm from two different points of view.



The numerical solution for 11-mm can be found in a similar way.



View 11-MMO from two sides:



Did I really get the right decisions? Maybe not. For these symmetries, I'm sure that I found a local maximum . For example, here is a function with a local maximum of 5 with a value of 1.



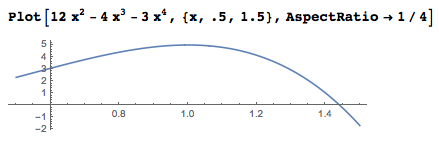
And if you look in the chart a little further, then you can find a global maximum of 32 with a value of -2.



In a similar Thompson problem, there is evidence for 12 vertices of the icosahedron, being in which a system of 12 electrons is in a potential minimum. But for 7, 8, 9, 10, 11 and 13+ electrons, the problem is considered unsolved. The Kepler hypothesis assumes that the hexagonal dense package is the closest package for the spheres, but strict evidence was obtained by Thomas Hales only on August 10, 2014. The densest packaging for regular tetrahedra — with a ratio of 4000/4671 = 0.856347 ... —was opened only on July 27, 2010, but still does not have strict proof. Any statements about the found solution should be perceived with a certain degree of skepticism; geometric maximization problems are known to be very complex.

For several months, my best solution for 11 points was at the local maximum, corresponding to an asymmetric MMO. Some (or most) of these solutions are likely local, not global, but which ones? With this reservation, you can look at the most famous solutions for 12 or more points.

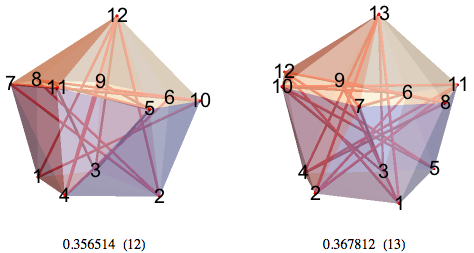
12-MMD has a vertex at point 12 and contains an irregular heptagon 11-6-7-10-8-5-9 and a quadrilateral 1-4-3-2.

13-MMD has a vertex at point 13 and contains an irregular heptagon 12-8-10-6-7-9-11 and the same pentagon 1-2-3-4-5.

My attempts to add symmetry led to figures with a smaller volume.



In theory, solutions for 14-mm should be very symmetrical, but I haven’t yet succeeded them. I spent some time optimizing the vertex-pentagon-pentagon system for 15-mm, however, using the random point method, the best solution was obtained, in which symmetry was sacrificed to volume.



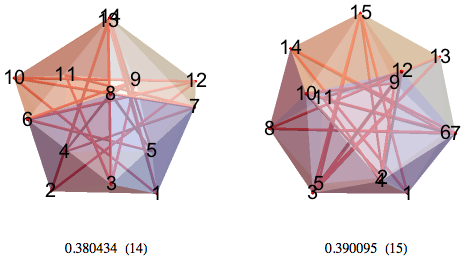
17-MWM, 18-MWM - I hope that in the first one everything is all right with symmetry.

As for the 19-mm and 20-mm, the 20-mm is not a dodecahedron, since single lines from the center are not the best option.



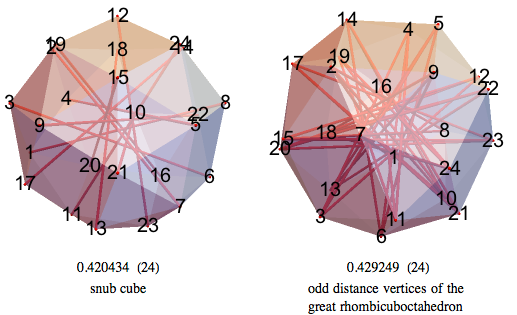
Both the “snub cube” and the half of the huge rhombocuboctahedron all have a smaller volume than the 24 NMM.



21-mm and 22-mm contains many seven- and nine-pointed stars.

23-HMM, 24-HMM - my best 24-HMM has tetrahedral symmetry.



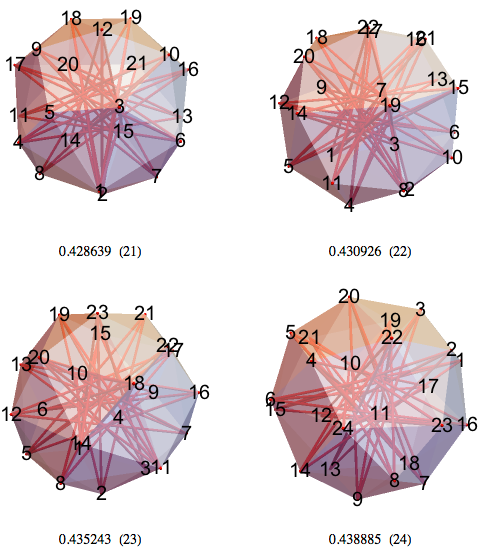
Here are some symmetries in the current best 24-mm. Segments 1-12 and 13-24 have corresponding lengths 0.512593 and 0.515168.



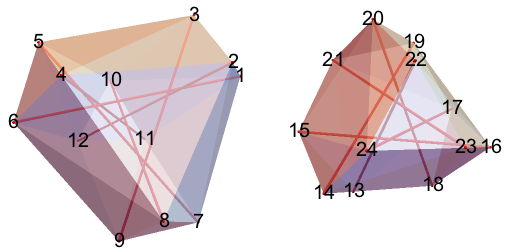
In 16-MMO and 17-MMO unit segments define polygons. 16-NMM contains many seven-pointed stars.



Below are the same polyhedra represented as solid bodies by means of ConvexHullMesh [], for HMMs 9-10-11-12, 13-14-15-16, 17-18-19-20, 21-22-23-24 , respectively.



Here is a table of the best currently known values.



Here are the best solutions that I found at the moment, for 4-24 points.



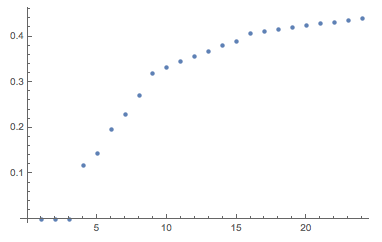
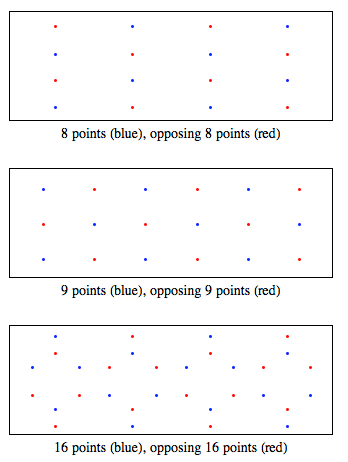
Let the points be located so that the maximum distance from the origin is as small as possible. The distribution shown below indicates the distances from the origin to the vertices of each polyhedron, each of which is from 8 to 24 vertices.



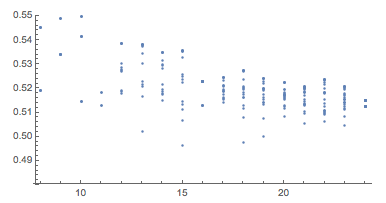
Using Mathematica 10.1, it was possible to obtain exact values ​​for 6,7,8,9-HMM and 16-HMM. Also, it was used to find very accurate, but numerical values ​​for 10-HMM and 11-HMM and managed to seriously advance with 24-HMM. Thus, we obtained solutions to seven previously unsolved problems in combinatorial geometry — all thanks to the combination of Volume [ ConvexHullMesh [points]] . And what innovations in Mathematica 10 helped you personally?

Bibliography

[1] B. Kind and P. Kleinschmidt, “On the Maximal Volume Convex Bodies with Few Vertices,” Journal of Combinatorial Theory , Series A, 21 (1) 1976 pp. 124-128.
doi: 10.1016 / 0097-3165 (76) 90056-X
[2] A. Klein and M. Wessler, “The Largest Small n-dimensional Polytope with n + 3 Vertices,” Journal of Combinatorial Theory , Series A, 102 (2), 2003 pp. 401-409.
doi: 10.1016 / S0097-3165 (03) 00054-2
[3] A. Klein and M. Wessler, “A Correction to the Largest Small N-dimensional Polytope with n + 3 Vertices,” Journal of Combinatorial Theory , Series A, 112 (1), 2005 pp. 173-174.
doi: 10.1016 / j.jcta.2005.06.001