Reliability Analysis in Wolfram SystemModeler 4.1

Translation of the post by Jan Brugård and Johan Rhodin " Reliability Analysis in SystemModeler 4.1 ".
Download the file with the models discussed in the post here .
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

Today we happily announce Wolfram SystemModeler 4.1 . In the future, a series of publications will be presented in which we will highlight the new functionality in the field of system reliability.

Several examples will be presented that you can try yourself by downloading a trial version of SystemModeler , a model from this post and a trial version of the Wolfram Hydraulic library.

Most people faced a situation where some thing that they bought and used in the future, suddenly for some reason breaks. Over the past few years, both authors of the article faced a similar problem - large-scale malfunctions with the engine in Johan’s car (it had to be replaced) and problems with the receiver of Jan, who had a verse (he had to be sent to a service center and changed the network chip).
')
In both cases, this caused problems for both consumers (among us) and manufacturers. These are just a couple of examples, and I am sure that you, too, will surely find a similar example.


Consumer electronics, satellite systems, systems for aviation - it does not matter, everything has certain reasons for assessing reliability.

Due to breakdowns, warranty costs may be required - as is the case with a network chip; the enormous difficulties associated with the repair - as in the case of the engine, and the satellite will require even more costs. As for the aircraft - there is already a direct threat to human life.

This begs the question - how models with quantitatively uncertain indicators can be used to improve the reliability and functionality of the system.

Implementing a system for analyzing reliability in SystemModeler allows you to calculate the reliability of the entire system through the reliability of its components. Let's get a look.

Let's start with the component level and calculate the probability of a hydraulic pipe failure:


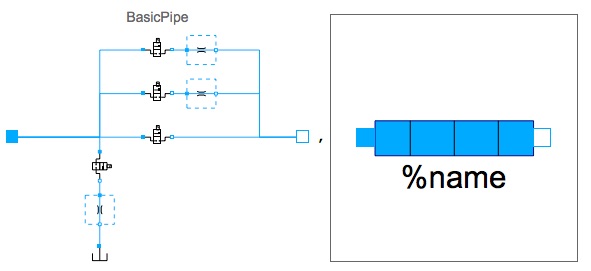
Chart diagrams for normal operation, limited operation, leakage and when the pipe is blocked are presented.

This is a fairly simple component that can be in three possible states of malfunction — leak, restrict, or be blocked.

Here is a system that includes three pipes in which we can consider different types of failure:


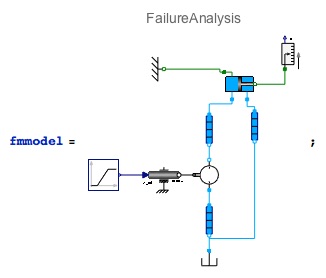
Model with three pipes, one cylinder and one pump. Pumping fluid causes the cylinder to push the rod, and the level changes.


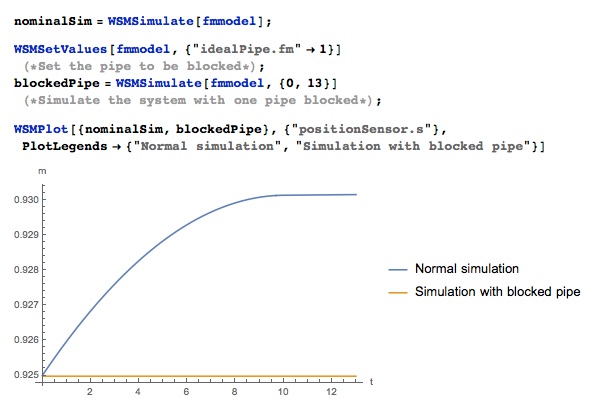
Fault detected! The level does not move at all when the pipe is locked.

You can determine the type of failure by looking at the simulation results, and make a list of probable causes of failure. In general, specialists in diagnostics and troubleshooting are engaged in this, and we will not particularly touch on this topic. Instead, in this post we will focus on the overall reliability of the systems, like the above.

The pipe operation can be illustrated with a classic fault tree, where a fault in one sheet causes a fault in the entire system:


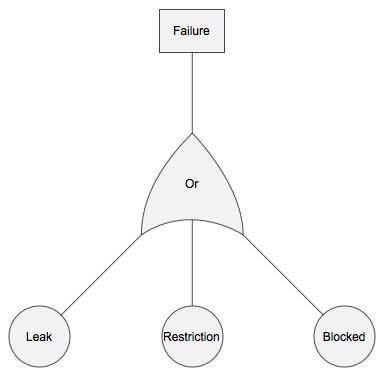
Fault tree for pipe.

With the new reliability approach in SystemModeler, we can specify the service life of individual components:


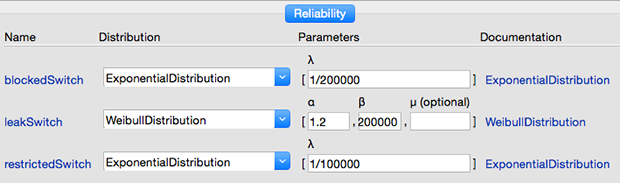
A robust approach in SystemModeler , where service life allocations correspond to individual components.

After that, we will construct a fault tree for the pipe, specifying which type of faults (leakage, limited transmission, complete blocking) will lead to system malfunction in general:


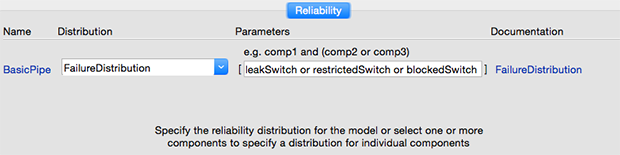
A robust approach to reviewing components with multiple service life distributions. This is where the fault tree is defined by entering a logical expression for this configuration.

Now the fault tree is available for analysis in Wolfram Language ( Mathematica ):



The WSMModelReliability function can return FailureDistribution (when it uses a fault tree), ReliabilityDistribution (when it uses a reliability block diagram), or a component's service life distribution. The traditional way to illustrate the reliability of components or systems is to use SurvivalFunction , which gives the probability that the system will be operational within time t. For one pipe it will look like this:



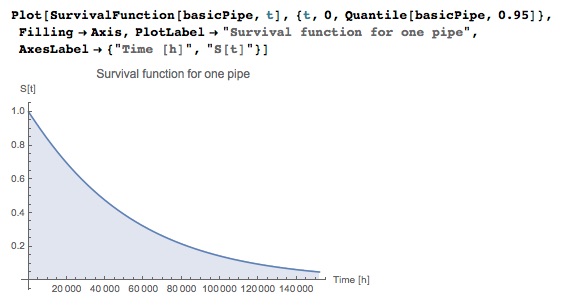
This distribution is like any probabilistic distribution in Wolfram Language. You can get more than 30 properties from it, for example, the conditional probability that the pipe will last more than 20,000 hours, considering that it has already worked 10,000 hours:



Symbol is a Conditioned conditional operator, and is a distributed distribution of a random variable. The code above can be read as follows: the probability that the pipe will still work after working 20,000 hours, if 10,000 hours have already been worked out .

Systems, of course, consist of a large number of pipes. Here is a diagram of the hydraulic system of the Cessna aircraft flaps, which contains several pipes (see the article on Habrahabr " Simulating aircraft flap failure scenarios using the Wolfram SystemModeler "):


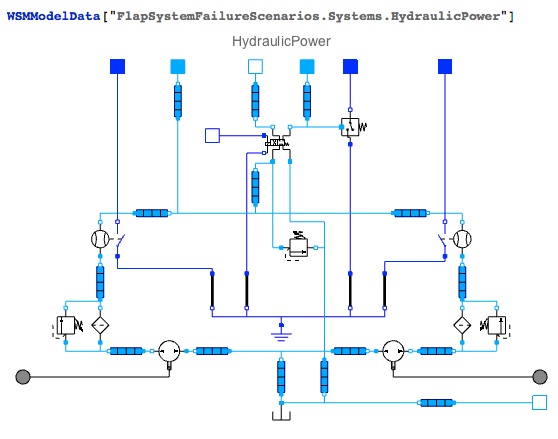
The hydraulic system of the flaps of a Cessna aircraft with one tank, two pumps, multiple valves and fifteen pipes.

SystemModeler automatically reads the embedded reliability values ​​of the pipes of the hydraulic system, as a result of which the reliability of the entire system can be calculated. The first question to consider is how much lower the reliability of the entire hydraulic system will be compared to a separate pipe:


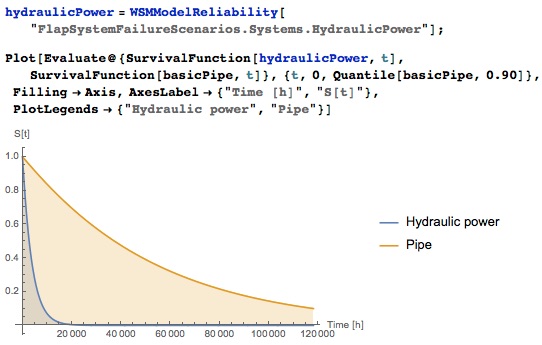
Comparison of the reliability of one pipe and the entire hydraulic system.

What should be expected - a system of many pipes is much less reliable than a single pipe. This is an illustration of the “weakest link” phenomenon: a failure in one pipe will cause the entire system to fail.

If we consider the same components of the flaps of an airplane, we will encounter something similar.

Now let's combine the hydraulic system with flaps (75 components in total). In SystemModeler, it suffices to indicate that we need a hydraulic system and a flap system ( hydraulicPower and flaps ).


Aircraft Cessna in terms of reliability. Here are the distribution of expected service life for the hydraulic system and flap system.




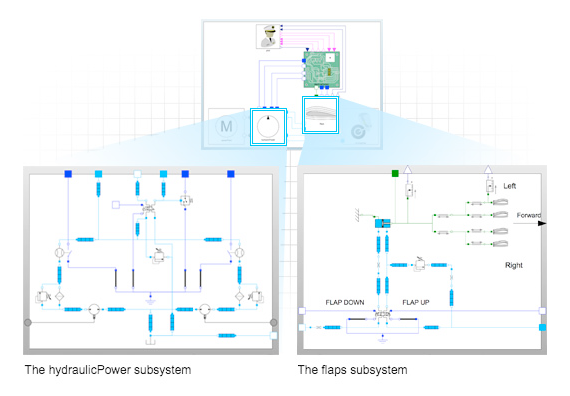
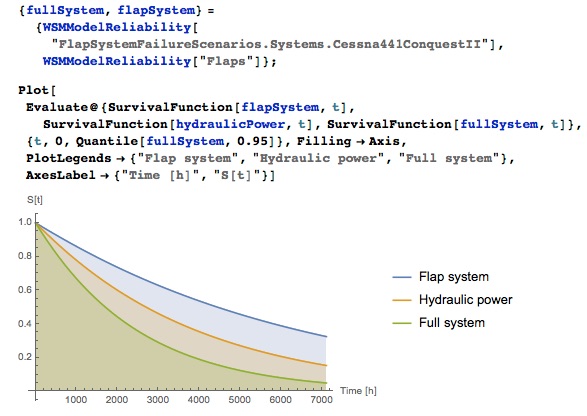
Reliability functions for various parts of the system.

The reliability of the entire system is lower than the reliability of each of the components. This law applies to all systems - the more components in the system, the higher the likelihood that some individual component will fail.

Let's now find out which of the components will be most advantageous to improve. The Wolfram Language contains nine different importance measure functions, the simplest of which is the StructuralImportance . Let us find out which faults are easiest to eliminate in the pipe:


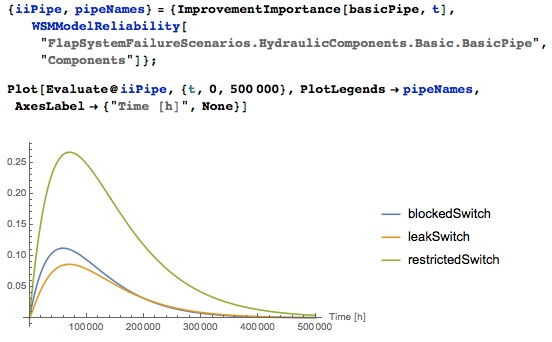
Potential improvements for various pipe faults.

The importance of improvement indicates how greatly the reliability of the system will increase when replacing a component with its ideal counterpart. The importance of improvement is a relative measure, and in order for it to have some meaning, it must be taken in the context of the whole system and its components. From the graph it becomes clear that the way to eliminate the limited pipe throughput will most of all increase the reliability of the system. You can do the same for the entire system and compare the flap system with the hydraulic system:


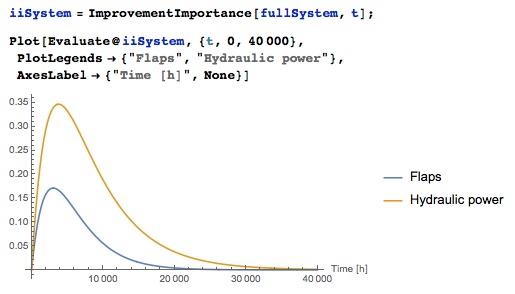
The improvement potential for the hydraulic system is definitely higher than for the flaps.

From this graph you can learn a few important points. First, the improvement of the hydraulic system compared with the improvement of the flaps has a higher level of payback in the context of the lifetime of the entire system. Secondly, the payback will be the higher, the greater the ratio (starting from 1.66) between the contributions to the improvement of the hydraulic system and the flaps. This is not particularly visible on the graph, but it becomes apparent when comparing numbers. For example, with a service life of 3.788 hours, when the hydraulic system has the highest value, the ratio will be 2.08, and with a service life of 10,000 hours, 3.38.

Reliability analysis shows where the main efforts should be focused on improving the system, thereby increasing the reliability of the product, assess where a failure can occur and bring the obtained data into compliance with the guarantee policy.

On the SystemModeler website, you can learn more about what is new in SystemModeler 4 by studying examples, free courses, exploring a fully functional trial version.

PS

In the previous post “ Simulation of aircraft flap failure scenarios using Wolfram SystemModeler ”, a malfunction in the electronic system was studied, and in the article “ Reliability Mathematics with Mathematica ” Mathematica functionality in the field of reliability analysis was covered in detail. Finally, from the free course on Modeling Safety-Critical Systems you can learn some of the modeling of faults in individual components and how they affect the behavior of the system as a whole.