Automaton like a jet engine: real physics of unreal flight

Translation of the post Malte Lenz " Machine Gun Jetpack: The Real Physics of Improbable Flight ".
Download the file with the models discussed in the post here .
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

Is it possible to fly with the help of an automaton using the reactive force arising from shots? This question was asked in the article What if? Randall Munrow “ Machine Gun Jetpack ” ( translation of the post into Russian). It turns out that it is possible, because some automata create enough strength to lift their own weight, and maybe even a little more. In this post I will explore the dynamics of automata firing down, as well as the forces acting at the same time, the generated speeds and how much height can be raised in this way. I will also duplicate the warning from the article: please do not repeat this at home. For this there are software environments for modeling.


Automatic with a squirrel on the stock

Let's start with something smaller than a person. For example, with this gray squirrel. We will plant a squirrel on a butt, open fire from a machine gun in automatic mode and see what happens. To simulate the dynamics of this system, I will use Wolfram SystemModeler .


Automaton model
')
In the image above, you can see the machine. An automaton as a system consists of cartridges and the automaton itself, moreover, they all have masses and are subject to gravity. They are easy to create by simply combining the built-in mechanical components:


Mass, under the influence of the gravitational force of the Earth

The magazine is a more complex component, because with every shot a mass is ejected - the bullet itself and the cartridge case. With each shot from the mass of the loaded magazine is subtracted the mass of the bullet and the mass of the sleeve. That is, the mass multiplied by the number of shots is subtracted from the initial mass.

Combining this with a simple model of a squirrel, adding a height sensor above the ground and a collision sensor, which, when triggered, completes the simulation, we get the full model.



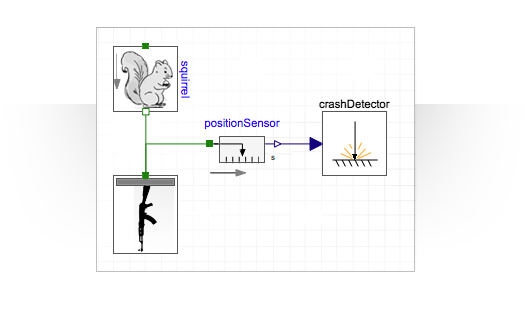
To correctly conduct a simulation, you will need to set the values ​​of the parameters of various components. I will use a gray squirrel , which usually weighs about 0.5 kg.



Then I need the data on the machine. I will use the ubiquitous 7.62-mm Kalashnikov assault rifle (AK). Here are some data on it:



Automatically generated thrust can be calculated based on the mass of the bullet, its muzzle velocity and the number of shots per second:



Then it would be possible to estimate the duration of each shot, that is, the time during which the bullet passes through the barrel. We introduce the assumption that the average speed in the barrel is half of its muzzle velocity:



The strength at this point in time can be calculated through thrust:



Now all the parameters that are needed to simulate the flight of a squirrel on the machine are set:



We will carry out a simulation of a protein-machine system with one cartridge:



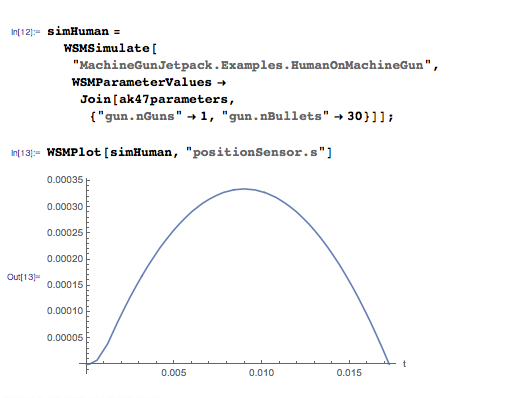
If we consider how the altitude will change depending on time, you can see that the squirrel will reach a height of 9 centimeters, and the flight time will be 0.27 seconds.



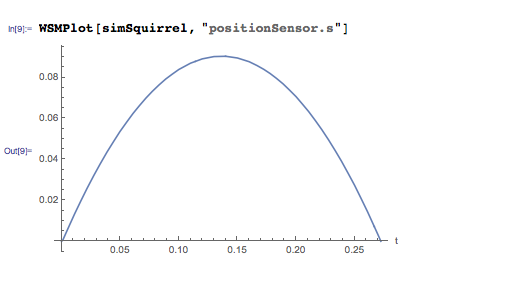
Or, in other words,



the squirrel is not particularly high. What is the obvious solution to this problem? Of course, you should add cartridges. Standard store contains 30 pieces:



This gives us almost 5.8 seconds of flight, and the squirrel rises to a dizzying height of 17.6 meters. Very frightening height for humans, but perhaps not for squirrels.



Here is how far she flew:



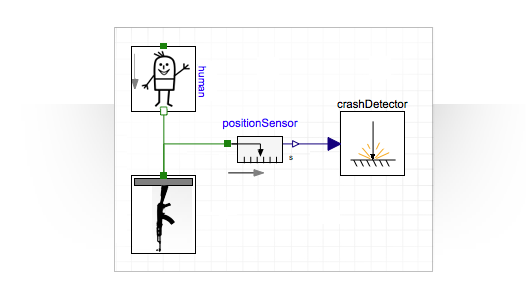
I showed that the squirrel can fly while sitting on the machine. Let's now see how high a person can fly if we defuse a magazine of 30 rounds:





One machine, perhaps, is not enough. Need to take them more. We introduce a parameter that will correspond to the number of automata and take values ​​in the range from 1 to 80:





There is something interesting here. The effect of 50 machines and more of them can easily be explained. The more of them, the more power, that is, the height of the flight will be higher. However, the simulation with the 15th and 32 machine guns is a bit more interesting. Let's take a closer look at the version with 15 machines. The red dots correspond to the moments of the shots, that is, the machine gun shoots a bullet every 100 ms:



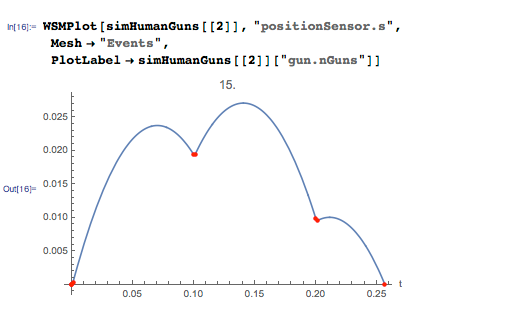
You can see that the whole system flies slightly, then begins to fall, then, after the next shot, flies up again, but at a slightly higher altitude, and then drops lower than the previous time. You can also follow the change in speed over time:



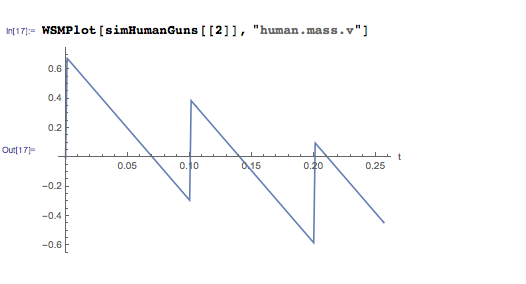
Before the first shot, the whole system is on the ground and, accordingly, has zero speed. Then the absolute speed increases dramatically, but before the next shot has time to fall below zero. That is, after the next salvo, there is a drop in speed, as a result of which the system begins to move downwards, but there are still cartridges in the store. But then there will be just small jumps from a place.



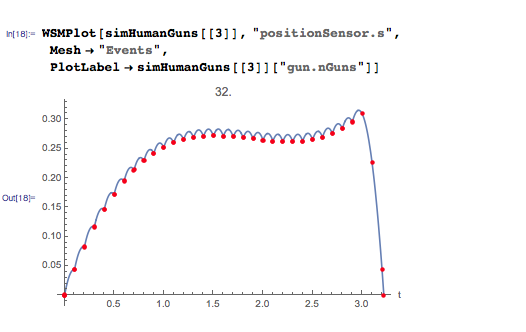
In the scenario with 32 automatic machines, a slightly different behavior is observed. The beginning resembles the behavior of a system with 15 automatic machines - the same speed, and the absolute speed is lost with each volley, as a result of which the system rushes down. However, somewhere in 2.5 seconds after the start, the system begins to climb, until all the ammunition is consumed.

This is due to the change in mass of the store over time:



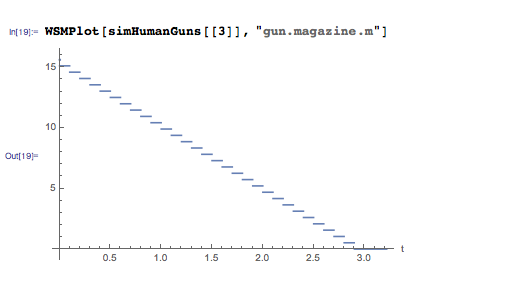
You can see that with each shot the store loses mass - the mass of bullets and shells. Because of this, the system becomes light enough to begin to climb. This indicates that there is a certain limit on the number of cartridges with which each machine can be supplied while maintaining the possibility of flight — another interesting parameter that can be varied. Let's try to fly with the following capacities of the machine shop:



Since the more automata, the more power, we take, say, a thousand pieces:



If you take a thousand machines, it turns out that supplying 165-rounds of cartridges to each one is not the best option:



This is because if you take too many bullets, the system will become too heavy for flying. Now that I have received a reasonable (if this word is generally applicable to flights on machine guns) the number of cartridges for flight, let's see what height can be achieved by changing the number of machine guns. One would expect that the more automata, the higher the flight and the longer the flight time.



Here is the dependence of the maximum heights on the number of automata:



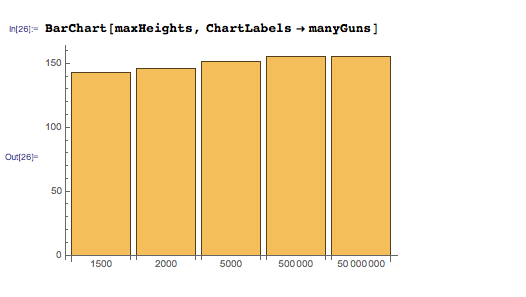
As it turns out, a significant increase in the number of automata (from 1500 to 50 million) gives a very slight increase in the maximum height. This is because the number of automata increases, the specific gravity of a person per each automaton decreases, until each automaton lifts only its own mass with a small additional mass. It turns out that the system will be able to achieve the same maximum height as a single automaton, but without additional weight, and the increase in the number of automata ceases to give any advantages.

To summarize the above: the best jet engine from automata should contain at least 5000 AK with 145 ammo cartridges in the store.


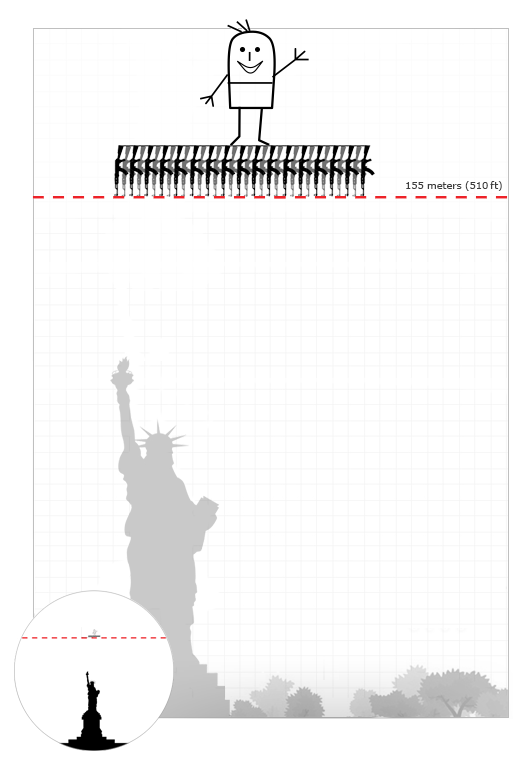
How high can you fly up with the help of automata?