Muller's recurrent relation: problems with rounding floating-point numbers
Some time ago I came across an exercise that doesn’t look that difficult:
Let the sequence x n be defined as:
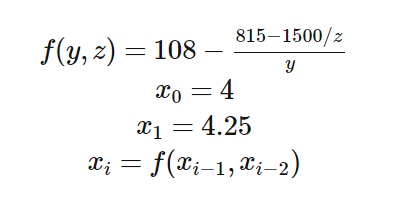
count x 30 .
This is not so difficult to encode, perhaps implementing x i as a recursive function. With ordinary double-precision floating point numbers, as i increases, the result converges nicely to 100. Super!
')
Unfortunately, 100 is not even the closest answer. In fact, the sequence converges to 5.
This sequence is known as the Muller Recurrent Relationship and has been synthesized specifically to demonstrate how quickly and dramatically round-off floating-point errors lead to catastrophic results, under the right (well, wrong) conditions. This paper (pdf) details the various dangers of rounding, in particular, and this sequence (p. 14). Another description of the problem can be found here (pdf) .
I think that many programmers, including me, realize that the math of floating-point numbers can go wrong in some situations, but dismiss the problem, believing that this can happen only if very large or very small numbers are involved in the calculations, or when accumulates a huge number of errors. This exercise with innocent-looking constants and a small number of iterations perfectly demonstrates that rounding errors can have a significant impact even besides extreme numbers. In this case, the instability of a fixed point 5 leads to the fact that even small errors significantly change the result.
I can add nothing more, but I think that this problem is worth sharing.
We can compare the first hundred values of a sequence between ordinary floating point numbers and arithmetic with arbitrary precision using a short Mathematica program. We use the convenient syntax of Mathematica memos, so the calculations take place quite quickly even for 100 or more iterations.
f [ y_ , z_ ] : = 108 - ( 815 - 1500 / z) / y;
xExact [ 0 ] = 4 ;
xExact [ 1 ] = 17/4 ;
xExact [ n_ ] : = xExact [n] = f [ xExact [n - 1 ], xExact [n - 2 ]];
xFloat [ 0 ] = 4 ;
xFloat [ 1 ] = 4.25 ;
xFloat [ n_ ] : = xFloat [n] = f [ xFloat [n - 1 ], xFloat [n - 2 ]];
TableForm [
Table [{i, N [ xExact [i], 20 ], N [ xFloat [i], 20 ]}, {i, 0 , 100 }],
TableHeadings ->
{ None , { "i" , "x [i] \" exact \ "" , "x [i] floating point" }}
Let the sequence x n be defined as:
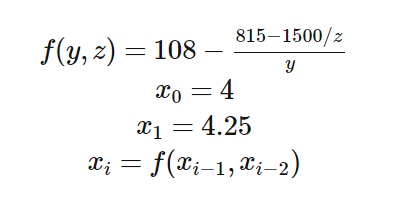
count x 30 .
This is not so difficult to encode, perhaps implementing x i as a recursive function. With ordinary double-precision floating point numbers, as i increases, the result converges nicely to 100. Super!
')
Unfortunately, 100 is not even the closest answer. In fact, the sequence converges to 5.
Problem
This sequence is known as the Muller Recurrent Relationship and has been synthesized specifically to demonstrate how quickly and dramatically round-off floating-point errors lead to catastrophic results, under the right (well, wrong) conditions. This paper (pdf) details the various dangers of rounding, in particular, and this sequence (p. 14). Another description of the problem can be found here (pdf) .
I think that many programmers, including me, realize that the math of floating-point numbers can go wrong in some situations, but dismiss the problem, believing that this can happen only if very large or very small numbers are involved in the calculations, or when accumulates a huge number of errors. This exercise with innocent-looking constants and a small number of iterations perfectly demonstrates that rounding errors can have a significant impact even besides extreme numbers. In this case, the instability of a fixed point 5 leads to the fact that even small errors significantly change the result.
I can add nothing more, but I think that this problem is worth sharing.
Calculating the correct result
We can compare the first hundred values of a sequence between ordinary floating point numbers and arithmetic with arbitrary precision using a short Mathematica program. We use the convenient syntax of Mathematica memos, so the calculations take place quite quickly even for 100 or more iterations.
f [ y_ , z_ ] : = 108 - ( 815 - 1500 / z) / y;
xExact [ 0 ] = 4 ;
xExact [ 1 ] = 17/4 ;
xExact [ n_ ] : = xExact [n] = f [ xExact [n - 1 ], xExact [n - 2 ]];
xFloat [ 0 ] = 4 ;
xFloat [ 1 ] = 4.25 ;
xFloat [ n_ ] : = xFloat [n] = f [ xFloat [n - 1 ], xFloat [n - 2 ]];
TableForm [
Table [{i, N [ xExact [i], 20 ], N [ xFloat [i], 20 ]}, {i, 0 , 100 }],
TableHeadings ->
{ None , { "i" , "x [i] \" exact \ "" , "x [i] floating point" }}
Results:
ix [i] "exact" x [i] floating point -------------------------------------------------- - 0 4.00000000000000000 4.0000000000000000000 1 4.25000000000000000000 4.25 2 4.4705882352941176471 4.47059 3 4.6447368421052631579 4.64474 4 4.7705382436260623229 4.77054 5 4.8557007125890736342 4.8557 6 4.9108474990827932004 4.91085 7 4.9455374041239167248 4.94554 8 4.9669625817627005987 4.96696 9 4.9800457013556311613 4.98004 10 4.9879794484783922601 4.98791 11 4.9927702880620680975 4.99136 12 4.9956558915066340266 4.96746 13 4.9973912683813441129 4.42971 14 4.9984339439448169190-7.81676 15 4.9990600719708938678 168.943 16 4.9994359371468391480 102.04 17 4.9996615241037675378 100.1 18 4.9997969007134179127 100.005 19 4.9998781354779312492 100. 20 4.9999268795045999045 100. 21 4.9999561270611577381 100. 22 4.9999736760057124446 100. 23 4.9999842055202727079 100. 24 4.9999905232822276594 100. 25 4.9999943139585595936,100. 26 4.9999965883712560237 100. 27 4.9999979530213569080 100. 28 4.9999987718123113300 100. 29 4.9999992630872057846 100. 30 4.9999995578522583059 100. 31 4.9999997347113315242 100. 32 4.9999998408267904691 100. 33 4.9999999044960712411 100. 34 4.9999999426976416502 100. 35 4.9999999656185845961 100. 36 4.9999999793711506158 100. 37 4.9999999876226903184 100. 38 4.9999999925736141727 100. 39 4.9999999955441684970 100. 40 4.9999999973265010958 100. 41 4.9999999983959006566 100. 42 4.9999999990375403937 100. 43 4.9999999994225242361 100. 44 4.9999999996535145416 100. 45 4.9999999997921087250 100. 46 4.9999999998752652350 100. 47 4.9999999999251591410 100. 48 4.9999999999550954846 100. 49 4.9999999999730572908 100. 50 4.9999999999838343745 100. 51 4.9999999999903006247 100. 52 4.9999999999941803748 100. 53 4.9999999999965082249 100. 54 4.9999999999979049349 100. 55 4.9999999999987429610 100. 56 4.9999999999992457766 100. 57 4.9999999999995474659 100. 58 4.9999999999727284796 100. 59 4.9999999999998370877 100. 60 4.9999999999999022526 100. 61 4.9999999999999413516 100. 62 4.9999999999999648110 100. 63 4.9999999999979788866 100. 64 4.9999999999999873319 100. 65 4.9999999999999923992 100. 66 4.9999999999999954395 100. 67 4.9999999999999972637 100. 68 4.9999999999999983582 100. 69 4.9999999999999990149 100. 70 4.9999999999999994090 100. 71 4.9999999999999996454 100. 72 4.9999999999999997872 100. 73 4.9999999999999998723 100. 74 4.9999999999999999234 100. 75 4.9999999999999999540 100. 76 4.9999999999999999724 100. 77 4.9999999999999999835 100. 78 4.9999999999999999901 100. 79 4.9999999999999999940 100. 80 4.9999999999999999964 100. 81 4.9999999999999999979 100. 82 4.9999999999999999987 100. 83 4.9999999999999999992 100. 84 4.9999999999999999995 100. 85 4.9999999999999999997 100. 86 4.9999999999999999998 100. 87 4.9999999999999999999 100. 88 4.9999999999999999999 100. 89 5.00000000000000000 100. 90 5.00000000000000000 100. 91 5.00000000000000000 100. 92 5.00000000000000000 100. 93 5.00000000000000000 100. 94 5.00000000000000000 100. 95 5.00000000000000000 100. 96 5.00000000000000000 100. 97 5.00000000000000000 100. 98 5.00000000000000000 100. 99 5.00000000000000000 100. 100 5.00000000000000000 100.
Source: https://habr.com/ru/post/258483/
All Articles