The history and future of special features

Translation of Stephen Wolfram's article " The History of the Future of Special Functions ".
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

The article is a recording of a speech made at the Wolfram Technology Conference 2005 in Champaign, Illinois, as part of an event in honor of the 60th birthday of Oleg Marichev .

So, well, now I would like to return to the topic that I raised this morning. I would like to talk about the past and the future of special functions. Special functions have been my hobby for at least the past 30 years. And I think my work has had a significant impact in promoting the use of special functions. However, it turned out that I had never raised this topic before. Now it's time to fix it.


The history of many concepts and objects of mathematics can be traced from the time of ancient Babylon. After all, 4000 years ago in Babylon, 60-year arithmetic with various complex operations was developed and actively used.

At that time, addition and subtraction operations were considered fairly simple. But this did not apply to multiplication and division operations. And in order to produce such actions, some similarities of special functions were developed.

In fact, the division was reduced to the addition and subtraction of reciprocals. And multiplication in a rather cunning way was reduced to addition and subtraction of squares.

Thus, practically any calculations were reduced to work with tables. And, of course, archaeologists had to find the Babylonian clay tablets with tables of reciprocals and squares.

That is, the Babylonians already had the idea that there are some pieces of mathematical or computational work that can be used many times, obtaining very useful results.

And, to some extent, the history of special functions begins with the discovery of principles for working with sequences of these very “pieces”.

The following “pieces” were probably those that include trigonometry. Egyptian papyrus of Rinda from 1650 BC already contained some problems regarding the pyramids, the solution of which required trigonometry. It is worth mentioning that a Babylonian plate with a table of secures was found.

The astronomers of those times with their model of epicycles, of course, already with might and main used trigonometry. And, again, all mathematical operations came down to working with a small number of “special” functions.

Much attention was paid to what they called chords and arcs. Here is a picture.



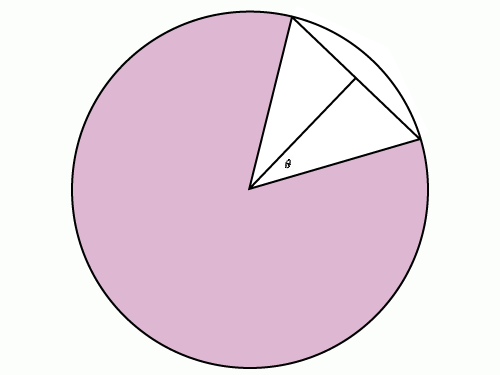
There are two radii of a unit circle with a certain angle between them. What is the length of the chord between them? Now we map the angle to the length of the chord called the sine function of the angle.

And here is the inverse problem: for some chord length - what will be the angle? Undoubtedly, we now call it arcsine.

The Greek astronomers took their chords and arcs very seriously. Almagest Ptolemy is full of them. And, they say, about 140 BC. Hipparch collected 12 volumes with tables of chords.

Well, ideas about trigonometry began to spread from Babylon and Greece. Trigonometry quickly acquired various standards and rules. Hipparchus has already adopted the idea of ​​a 360-degree circle from the Babylonians.

And, from the Indian word "chord", literally translated into Arabic and then incorrectly translated into Latin, the word "sine" appeared. It was in the 12th century, and at the beginning of the 13th century, Fibonacci began to actively use it.

In the 14th century, trigonometry became widespread. And in the middle of the 16th century, it played an extremely important role in the work of Copernicus - De Revolutionibus . This work for a long time has become in its way fundamental for those who have worked with mathematical functions.

It was then that trigonometry almost completely gained its modern look. Of course, there are several significant differences. For example, the constant use of versinus. Has anyone ever heard of this? In essence, this is 1 - Cos [x] . You can find it in trigonometric tables, which were published until very recently. However, now a couple of extra arithmetic operations are not a problem at all, so there is no need to talk more about this function.

Well, after trigonometry, the next big break was logarithms. They appeared in 1614.



It was a way to reduce multiplication and division to addition and subtraction.

Over the course of several years, many logarithmic tables have appeared. The use of tables, in fact, has become a ubiquitous standard that has existed for more than three hundred years.

It took several years for the natural logarithm and the exhibitor to take on its modern form. But in the middle of the 17th century, all the elementary functions we were accustomed to appeared. And from then until now, they are, in fact, the only explicit mathematical functions that most people will ever know about.

Well, it turns out, calculus appeared at the end of the 17th century. And this is the time from which special functions in the modern view began to appear. Many of them appeared soon enough.

Somewhere in the 18th century, one of Bernoulli put forward the idea that perhaps the integral of any elementary function would also be an elementary function. Leibniz thought he had a counterexample: 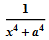. However, this expression was not. For several years, there have been active discussions about elliptic integrals . At least in terms of rows. And so the Bessel functions were discovered.

And by the 20s of the 18th century, Euler had just begun to dive into the world of computation. And he wrote about many of our standard special functions.

He discovered the gamma function as a development of the idea of factorial . He defined the Bessel functions in some applications, worked on elliptic integrals , introduced the zeta function , investigated polylogarithms .

Usually he did not give the functions certain names.

But gradually more and more functions about which he wrote began to be used by different people. And, often, after a period of their use, they already received some specific designations and names.

There were a few more bursts of activity in the appearance of special functions. At the end of the 18th century, there was a theory of potential and celestial mechanics. And, for example, the Legendre functions — which for a long time were called Laplace functions — appeared around 1780. In the 1820s, complex analysis became popular, and various doubly periodic functions began to appear. It cannot be said that in those days, communication between people was well established in this area. So in the end, various incompatible designations for the same concepts appeared. The problems that appeared then are still relevant today, and they often serve as a pretext for appeals to the Mathematica support service.

A few years later the harmonic analysis gained momentum, as a result of which various orthogonal polynomials appeared - Hermite, Leigger, and so on.

Well, already at the beginning of the 19th century it was clear that a whole “zoo” of special functions was emerging. And this made Gauss think about how to combine all this.

He investigated the hypergeometric series, which, in fact, were already discovered in the 1650s by Wallis and named after him. And he noticed that the function 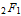( Gauss hypergeometric function ) actually encompasses many known special functions.

By the middle of the 19th century, special attention was given to special functions, especially in Germany. At this time there was a lot of literature on this subject. Therefore, when Maxwell wrote his works on electromagnetic theory in the 70s of the 19th century, he did not have to spend much time on the mathematical apparatus of special functions; there was already a lot of literature that could be referenced.

In addition to purely scientific papers describing the properties of functions, tables with their values ​​were created. Sometimes by people that no one really heard about. And sometimes very famous - among them Jacobi, Airy, Maxwell.

So, long before the end of the 19th century, almost all the special functions that we deal with today have already been created. But there were others. For example, has anyone heard of what a Gudermanian is ? I remember meeting him in reference books when I was a child. Gudermanian named after Christophe Guderman, a student of Gauss. It establishes the relationship between trigonometric and hyperbolic functions and is closely related to merchant cartographic projections. However, the Gudermanian practically does not occur in modern literature.

Well, a large number of intellectual resources have been invested in the development of special functions in the last few decades of the 19th century. I think everything could develop in the direction of the theory of invariants, syzygy, or to some other characteristic mathematical aspirations of the Victorian era. Indeed, the typical love of pure mathematics for abstractions and generalizations made special functions arbitrary and not particularly connected. It’s like learning some strange animals at a zoo instead of studying general biochemistry.

However, progress in theoretical physics re-activated interest in special functions. Mechanics. Theories of elasticity. Electromagnetic theory. Then, in the 1920s, quantum mechanics, in which even the most basic tasks required the use of special functions, such as the Laguerre and Hermite polynomials . And then there was the theory of scattering, which, perhaps, used almost the entire "zoo" of special functions.

This gave rise to the idea that any problem in its pure form can always be somehow solved in terms of special functions. And, without a doubt, the textbooks promoted this idea. Because the problems discussed in them are very succinctly formulated in terms of special functions.

Of course, there were some gaps. Fifth degree polynomials. The task of three bodies. However, they were too nonstandard. Not what was required for modern probabilistic theories.

In general, the scope of special functions is very extensive. The creation of tables gained a lot of momentum, especially in England. In essence, this area had a strategic importance of national importance. In particular, for things like navigation. Many tables were published. Here, for example, a good selection of the year 1794. When I first saw them, I thought that there was a place for a temporary shift to be.


(In fact, this Wolf was an officer of the Belgian artillery. I think I have no more relatives with him than with St. Wolfram, who lived in the 7th century of our era).

Tables played an important role at that time, which caused the appearance of the Babbage difference machine in the 1820s, which was designed to compile accurate tables. And by the end of the 19th century, special functions were the basis for their compilation.

Mechanical calculators became increasingly popular, and in Britain and the United States there were large-scale projects to create tables of special functions. For example, as a WPA project ( Works Progress Administration project ) in the 30s, when during the Great Depression, people were occupied with calculating the values ​​of mathematical functions.

Then began serious work on the systematization of their properties. Each had a lot of work, but the contribution of each was not particularly large. Although everyone thought they were important. By the way, here is the cover of the American Jahnke and Emde, which was first published in 1909, and in the 30th, got illustrations.



And very good, by the way.



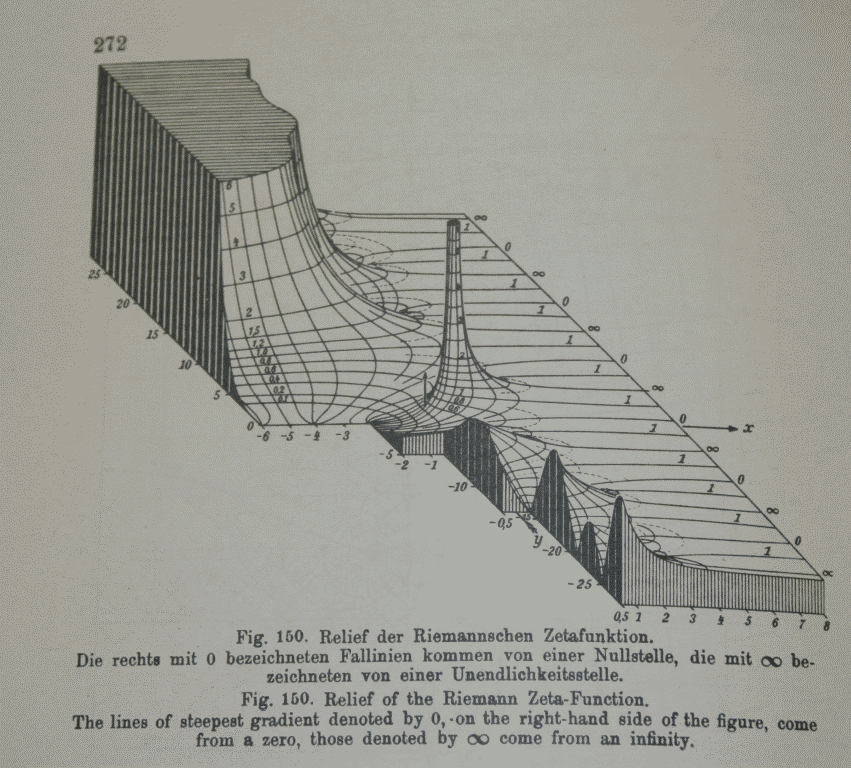
At the beginning of the 20th century, the creation of three-dimensional models of functions made of plaster and wood was popular. And yes, I had an idea to illustrate the zeta function, which I used to cover the first edition of The Mathematica Book by Jahnke and Emde.



During the Second World War, many studies were carried out on special functions, and it is difficult to explain why. This was probably due to some military needs. Although, I tend to think that it was just a coincidence. However, the potential connection with some strategic measures should not be dismissed.

And so, the first edition of Magnus and Oberhettinger was published in 1943.



On the basis of it appeared the first edition of Gradstein-Ryzhik .

In 1946, Harry Bateman died, leaving a large archive of all information on special functions. In the end, his insights were published under the name Bateman Manuscript Project.

The Manhattan project, and later the hydrogen bomb development project, also served as customers and consumers of special functions. In 1951, for example, Milt Abramowitz (Milt Abramowitz) of the National Bureau of Standards worked on the Coulomb wave function tables that he needed in nuclear physics.



From this, the book of Abramowitz-Stigan, published in 1965, gradually grew, becoming the number one literature for people in America using special functions.



In the 60s and 70s, much attention was paid to the development of numerical algorithms for computers. And the calculation of special functions was a favorite place.

The work in most cases was painfully specific - an enormous amount of time could be spent on some particular Bessel function of a particular order with a certain accuracy of calculation. But gradually there were libraries with collections of certain algorithms for calculating special functions. However, still a large number of people still use reference books with tables, which can often be seen in the most prominent places in academic libraries.

I started doing special functions when I was a teenager - in the mid-1970s. Official mathematics, which I studied at school in England, deliberately avoided special functions. It consisted in using some tricky tricks to find the answer using only elementary functions. I didn't really like it. I wanted something more general, more practical. Less ingenious. And I liked the idea of ​​special features. They seemed like a better tool. However, their discussion in books on mathematical physics never seemed quite systematized. Yes, they were more powerful features. But they still seemed somewhat arbitrary: something like a zoo of curious creatures with impressive sounding names.

I think I was about 16 when I first started using special functions for some real tasks. It was a dilogarithm. He was in a work on particle physics . And I am ashamed to say that I simply denoted it as f .



However, in my defense, I will say that polylogarithms were not studied at that time. The usual books on mathematical physics contained Bessel integrals, elliptic integrals, orthogonal polynomials, and even hypergeometric functions. But no polylogarithms. As it turned out, Leibniz also wrote about them. But for some reason they did not get into the usual "zoo" of special functions; and the only real information about them that I was able to find in the mid-1970s was in the 1959 book on microwaves by engineer Leonard Lewin.

Soon after, I often had to calculate integrals for Feynman diagrams. And then I realized that polylogs are the key, this is what is needed. Polylogarithms became my true friends, and I began to study their properties.



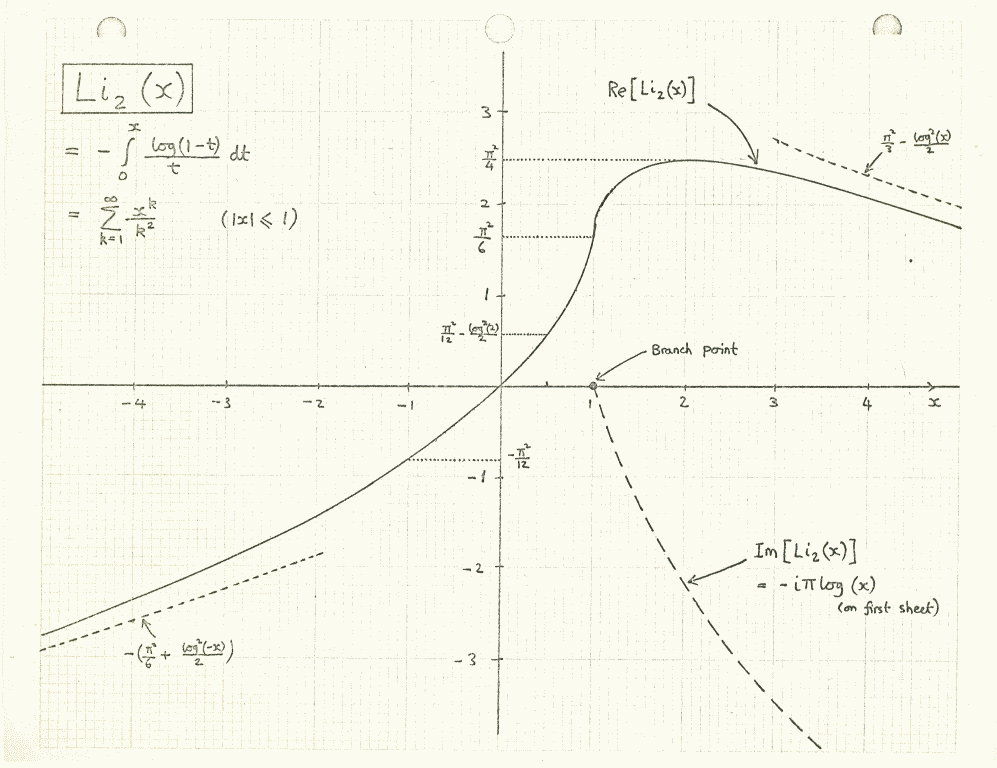
And there was something that I noticed then, the meaning of which I was really aware of only a long time later. I should clarify that the ability to work well with integrals at the time was a kind of visiting card of a theoretical physicist.

Actually, I would never say that I have any talents in algebra. However, somehow I found that if you use some fancy special functions, you can take integrals much faster and more conveniently. I was even asked to integrate something often. It seemed to me quite surprising. Especially considering that I simply wrote down any integral as a parametric derivative of the integral of the beta function.

This led me to the idea that the integration process can be greatly facilitated by working with some more common functions, and then moving back. Approximately how to solve a cubic equation in a complex form and then move on to real numbers. Anyway, there are many other examples of this in mathematics.

So, somewhere in the 78th, I realized that I had to write code and automate the process of taking all these integrals. As an example, I can give a flowchart of a program on Macsyma, which I wrote then.



Combination of algorithms and table search. It really worked and was very useful.



In addition to polylogarithms, I also dealt with other special functions. K-type Bessel functions in cosmological calculations , for example.



Calculations in quantum chromodynamics marked the heyday of the zeta function in all its glory. I developed a theory of " event areas " that still finds applications in experimental physics. It was completely based on spherical harmonics and Legendre polynomials.

I remember the day when, when working through one theory of quantum chromodynamics, I came across a modified type 1 Bessel function . I have never met them before.

You know, the development of special functions is often matched by some interesting events. And indeed - it has always been great to work with tasks set in terms of special functions. It was pretty spectacular.

Sometimes it seemed quite funny to show some old mathematical physicist some kind of mathematical task. They looked at them as archaeologists at the fragments of ancient pots. If they had beards, they would scratch them. And it is worth noting that this could be the Laguerre polynomial.

And when someone said that his problem includes some special functions, there was the impression that it was about the fact that it was flavored with some sort of oriental spices. And yes, the East was also included in the work. Because somehow, at least in the USA at the end of the 1970s, it seemed that the special functions were very “Russian” in taste.

At least among physicists, the book by Abramowitz-Stigan was well known. And Yanke and Emde were virtually unknown. Like Magnus, Oberhettinnger and others. I believe that only the mathematicians knew the project of the manuscripts of Beitman (even in Caltech, where it was founded). However, in physics, Russian publications were very popular, especially Gradstein-Ryzhik.

I never fully understood why among the special functions there was such a strong Russian influence. It was said that this was because the Russians did not have good computers, and they had to do everything in the most analytical form possible. I think that is not entirely true. I think the time has come to tell the story behind Grodshtein-Ryzhik.



I still do not know the whole story, but I will tell what I know. In 1936, Joseph Moiseevich Ryzhik wrote a book called Special Functions, which was published by the United Scientific and Technical Publishing House (now Fizmatlit). Ryzhik died in 1941 - then, in besieged Leningrad, then at the front. In the 43rd handbook of formulas under the authorship of Ryzhik was published by the State Technical and Theoretical Publishing House (the same publishing house, which changed the name). The book itself formulates its goal as a solution to the problem with the lack of reference books with formulas. It says that some of the integrals given in this book are found for the first time, and the rest come from three books: the French in 1858, the German in 1894, and the American in 1922. The main efforts were aimed at systematization of integrals and some simplification of them due to the introduction of a new special function s , which is equal to . It expresses gratitude to three well-known mathematicians from Moscow State University. In fact, that's all we know about Ryzhik. More than about Euclid, but not by much.

Well, moving on. Israel Solomonovich Gradstein was born in 1899 in Odessa and became a professor of mathematics at Moscow State University. But in 1948 he was fired as part of the Soviet persecution of Jewish scholars. To earn, he wanted to write a book. And he decided to continue the business of Ryzhik. He probably never met him. But he made a new edition, and in the third edition the book was published under the authorship of Gradstein-Ryzhik.

Gradstein died of natural causes in Moscow in 1958. There was a legend that one of those who worked on the Gradstein-Ryzhik book was shot as part of anti-Semitic persecution because of an error in the tables, which resulted in a plane crash.

Meanwhile, starting around 1953, Yuri Geronimus, who worked with Gradstein at Moscow State University, began to help him with editing tables and added some applications for special functions. Then several more people were included in the work. And when the tables were published in the West, there were some questions about royalties. Geronimus is alive and well and now lives in Jerusalem - Oleg Marichev called him last week.

I think that integrals are something eternal. They do not bear the traces of their creators. So, we have tables, but in reality we don’t quite understand where they came from.

Well, in this way, in the late 1970s, I began to get rather serious about special functions. So, in 1979, when I started creating SMP , a kind of predecessor to Mathematica , I needed to add powerful support for special functions. It seemed obvious — to shift the mathematical routine to the computer.

Here is one of the earliest SMP concepts written in the first few weeks of the project. There are already some special functions.



Here is a little later.



SMP 1981- .



. , . . , , , . . . , — . .

, . 1986 Mathematica . — , , , .

, , , . , - . , . . : " , , 90- ".

, . , , . , . . A New Kind of Science — . .

, . .

, , , Mathematica . — . . , , . . . , .

, , , , , . FunctionExpand FullSimplify . .

. , . , , , , .

, . , . — . . , , .



. , , . , , .

, Mathematica . . . , Wolfram Functions Site . - , .

, . - , , , , , , . - , . - ( Wolfram|Alpha , . .). - . .

, . . , . . , , , , . , . . . Mathematica .

, Mathematica , . ? , , .

, Mathematica , — , . RSolve Sum DSolve Integrate . , , . 1859- 1860- — : A Treatise on Differential Equations A Treatise on the Calculus of Finite Differences . Mathematica .

, , , . . , , , 17- .

. , .

: . . , .

Wolfram Language ( Mathematica ). , . Mathematica , , .

? . ? , Mathematica, Wolfram Functions .

. -, . — . . .

, , . , . , , .

: - ? ? ? , Wolfram Functions Site. , , Wolfram Functions Site.



, Google-pagerank-.



, .



, , . , , . , , . - .

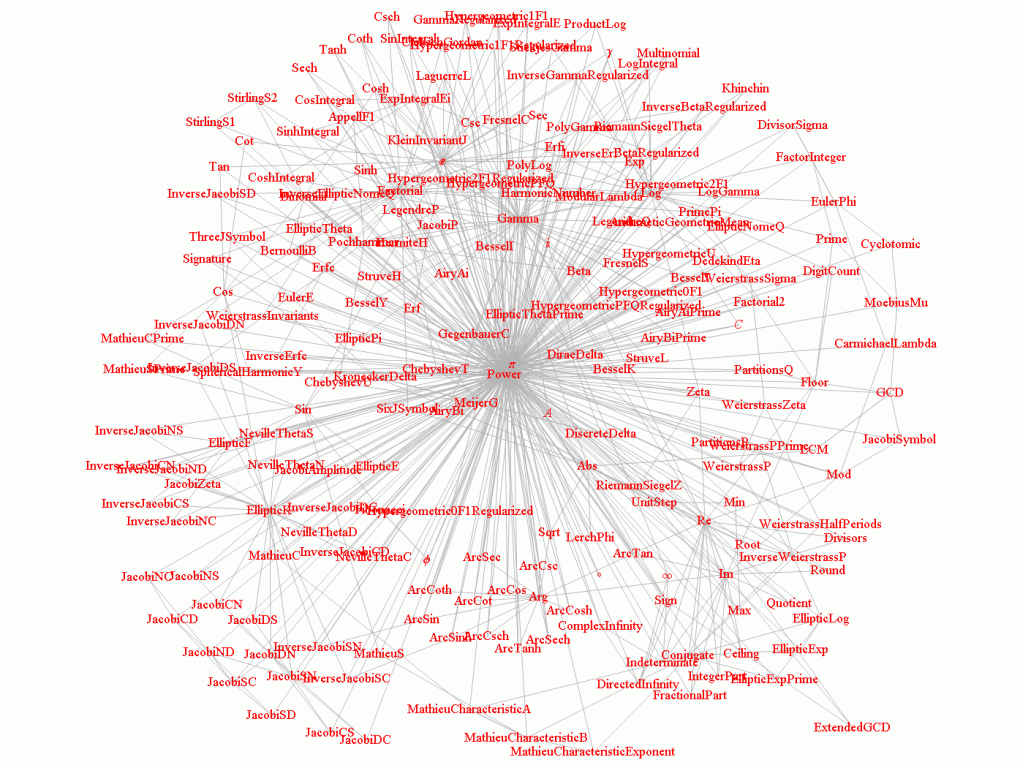
, , . , . , , , , , — . n . , . — .

p q - , . (Power) {0,0}. — {1,0}. (Erf) — {1,1}. BesselJ — {0,1}. EllipticK — {2,1}. 6- j — {4,3}. , , . , .

, : - , , , — . , .

— . Sum Mathematica . :



, . — - . .

, , .

, . : , .

, , . , , , , . DSolve . And here is the result.



. . - .

- . DSolve . . — DSolve ? , . - , .

, , . . , , Sin[Sin[x]] . , . . . , .

. Integrate Mathematica , . , , .

- : , ? , , , . . . . , , .

. . , , , , - . , . . .

? , ?

. , , .

, — . . , . — — . .

? . , .



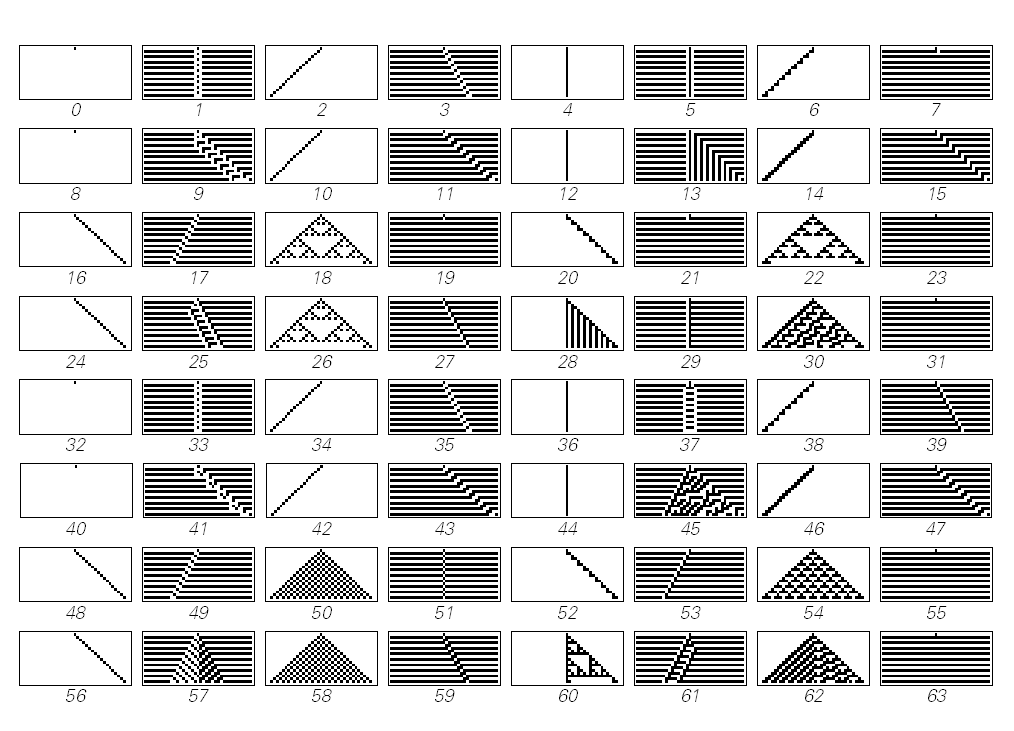
Many do quite simple things. And give the same structure. Or at least repetitive.

Let's try to imagine that we can find a formula to implement it. With this you can understand, for example, what color a certain cell will have at a certain step.

But what about this guy? My favorite rule 30?



Is there a formula to determine what happens after a certain number of iterations?

Or for this?



I do not think.

I think in fact such systems are inherently computationally irreducible .

We can consider such a system, as the 30th rule, as a process of calculation. If we try to predict what kind of result it gives us, then we also need to perform some calculations. And in some ways, the successes of such traditional areas as theoretical physics were in fact based on solving some much more complex systems than those we are studying. So we need to give some definition of what the system will do if it has much less computational capabilities than it needs.

Yes, one of the main ideas in my book is what I call the " Principle of Computational Equivalence ". This principle states that almost all systems whose behavior is not obviously simple are exactly equivalent to their computational complexity. Even in spite of the fact that both our brain and our mathematical algorithms can work with very complex rules, they cannot carry out calculations that are at least somewhat more complicated than, for example, what the 30th rule does. That is, this means that the behavior of the 30th rule is computationally irreducible: we cannot explain how the system will behave using a process that is more efficient than simply reproducing the 30th rule.

Thus, we can never get some exact solution for the 30th rule - say, a formula, the arguments of which will be the coordinate of the cell and the pitch, and the output of the function is the color of the cell.

By the way, this can be proved if the computational universality of the 30th rule is proved, that is, that it can be used to perform any calculations, to emulate any system. And this is the way to understand why this rule cannot have an exact solution. In a way, because this solution should be any possible calculation. Which means that it can not be some small formula.

Well, what follows from this with regard to special functions? Well, if we face large amounts of computational irreducibility, then special functions will not help us much. Because for many problems it will simply not be possible to make up some kind of formula - it does not matter, with special functions or with anything.

One of the main ideas of my book is that the computational irreducibility problem is solved very simply in the computational world of various programs. And the reason why we rarely encounter it is that such areas of knowledge as theoretical physics, specifically avoid computational irreducibility.

However, in nature, especially in such areas as biology, one may encounter a much wider sample of representatives of the computational universe. That is, there you can often find computational irreducibility. Theoretical sciences could not make much progress in this area.

Ok, now let's take a look at a system like the 30th rule, or, say, a small partial differential equation, which I found by exploring the space of all possible similar equations.



So why not some high-level special function that reflects what is happening in these systems?

Of course, we could just set a special function for the 30th rule. Or a special feature for this SHD. But it is a kind of deception. And the way we are going, makes us understand that a special function will be too “special”. Of course, purely nominally this would speed up the use of the 30th rule, or this SHD. But that’s all. It will not, like the Bessel function, resurface in a myriad of different tasks. It will serve only to solve this particular problem.

Let's try to summarize the above. The fact is that when there is a certain area of ​​computational irreducibility, there are many separate areas where it can be avoided. The meaning of a special function that will not be useless is that many different problems should easily be reduced to this special function.

It turns out that the scope of all problems in which there is no computational irreducibility includes standard special functions of the hypergeometric type. And what is outside this sphere? I think it is full of computational irreducibility. And full of fragmentation. So no new magic special function can appear that will immediately cover a multitude of problem areas. This is a bit like a situation with solitons and similar things. They are good in their field, but they are very specific. They live in some very narrow region of the space of various tasks.

Well, so how to formulate these concepts more generally?

You can think of analogs of special functions for a variety of different systems. Is there any limited set of special objects that, although they may require some kind of computation, but with the help of which it will be possible to get some other useful objects?

You might think about numbers. Numbers can be "elementary", rational, algebraic. But what then is useful “special” numbers? Of course, these are Pi , E , and EulerGamma . What about the other constants? The remaining constants fade away in the shadow of their more famous brethren. Perhaps, on the Wolfram Functions site there are not so many examples when there is some constant that pops up from time to time, but for which there is no name.

[The recording of the speech ends at this place]

---

The 10th version of the Wolfram Language (Mathematica) has hundreds of special features built into it.

You can learn more about them here:

• Lists (by groups) of special functions implemented in Wolfram Language (Mathematica)
• Article documentation on special functions in Wolfram Language