Introduction to discrete-oriented polyhedra for collision detection

Collision detection (collision detection) of virtual objects is a rather significant part for visualization tasks.

Task

And the challenge is to determine whether two objects collide (collide) or not.
The difficulty is that when testing visualization primitives directly with other primitives, the calculation of collisions takes unnecessarily large resources, especially with a huge number of objects involved in the simulation.

In order to facilitate such calculations and not to check directly between visualization primitives (which takes the most time), bounding volume technologies were invented, which allow describing visualization objects in such a way that collision testing does not take up such significant resources, although with small loss of accuracy.
')
In other words, bounding volumes are simple geometric shapes, into which more complex objects fit.

Bounding volumes

The most popular limiting volumes:
- Sphere (Sphere).
- A bounding box aligned along coordinate axes (Axis-aligned bounding boxes - AABB, sorry for translating).
- Object-oriented bounding boxes (OBB)
- Discrete-oriented polyhedra. (Discrete oriented polytopes - k-DOPs)
- other.


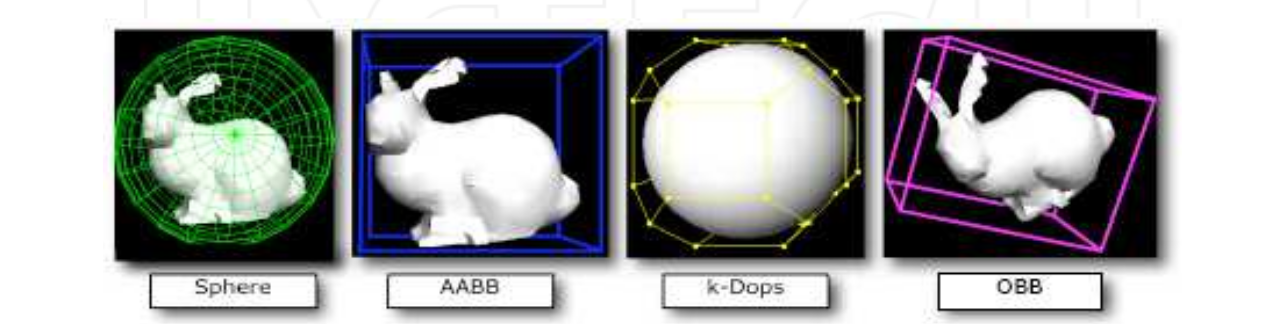
Figure 1. BV Review.

k-DOP

Each of them have a number of advantages and disadvantages, but we will focus on k-DOP.


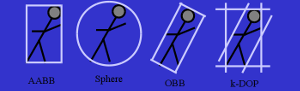
Figure 2. Lucidly about BV.

Discrete-oriented polytopes are a predetermined number of bounding planes and their orientations. K in the title describes the number of such planes.
For example, a two-dimensional 4-DOP is a common square, describing a certain two-dimensional object. In fact, AABB is a special case of k-DOP.

Two-dimensional AABB is the same square as 4-DOP.
And the three-dimensional AABB is the same cube as the 6-DOP.

But k-DOP can also use more planes. And, as was said, the orientation of such planes is chosen in advance and does not change.

The orientations of the planes are determined through direction vectors, the components of the normals of which are bounded by the set {-1, 0, 1}.

For example, for a regular square, 4 planes are needed with directions: (0, 1), (1, 0).
The directions of two planes are described here, but which limit the square below, above, to the left, and to the right. Although the total of 4 planes, therefore, it happens that they also write this way: (0, ± 1), (± 1, 0)

These normals allow you to seriously simplify the calculations.

Structure

k-DOP is described by only the minimum and maximum intervals (slabs) or distances. Two values ​​on one plane, which in the end it turns out quite simple to process and store.


Figure 3. Intervals in k-DOP.

For example, for a square, as we remember, we need 4 planes (k = 4). Hence, we need 2 (k / 2) minimum and 2 maximum values.


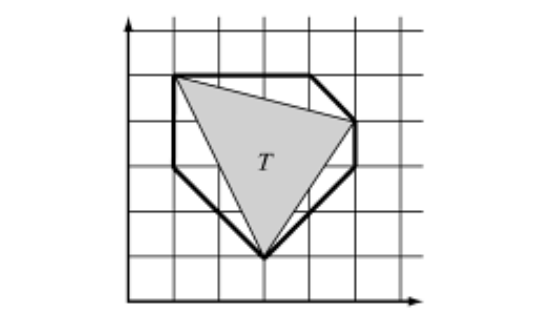
Figure 4. 8-DOP Describing Triangle.

In Figure 4, a triangle with coordinates (3, 1), (5, 4), (1, 5) is described using 8-DOP, i.e., eight planes and with direction vectors (1, 0), (0, 1), (1, 1), (1, -1).

Let's calculate the intervals describing this polyhedron.

Take the first plane with the direction (1, 0) and multiply by the coordinates:
3 * 1 + 1 * 0 = 3
5 * 1 + 4 * 0 = 5
1 * 1 + 5 * 0 = 1

The minimum value is 1, and the maximum 5.
The plane (1, 0) is defined by the values ​​1 and 5.
For the (0, 1) plane, the same values ​​are 1 and 5.
For (1, 1) - 4 and 9.
For (1, -1), –4 and 2.

Crossing check

If at least one plane does not intersect, then the whole structure also does not intersect.

Only if all the intervals / planes intersect, then the k-DOP structure itself intersects. But it should be noted that the described object may not intersect.

Therefore, it is said that if the k-DOP structures of two objects collide (collide), then their described objects may collide.

 bool overlapped (const KDop & a, const KDop & b, unsigned k)
 {
     for (unsigned i = 0; i <k / 2; ++ i)
     {
         if (a.min [i]> b.max [i] || a.max [i] <b.min [i])
         {
             return false;
         }
     }

     return true;
 }

Bounding Volume Hierarchy

As it turned out, the use of limiting volumes makes it easier to check for collisions, but loses a little in accuracy.

Therefore, for simple objects, in order to exclude unnecessary checks, first test their restrictive volumes, like AABB or k-DOP, and then go to primitives.
But with complexly structured objects, hierarchies of limiting volumes are applied. Often these are simply binary trees, where nodes define an object or a part of an object that is bounded by a volume.


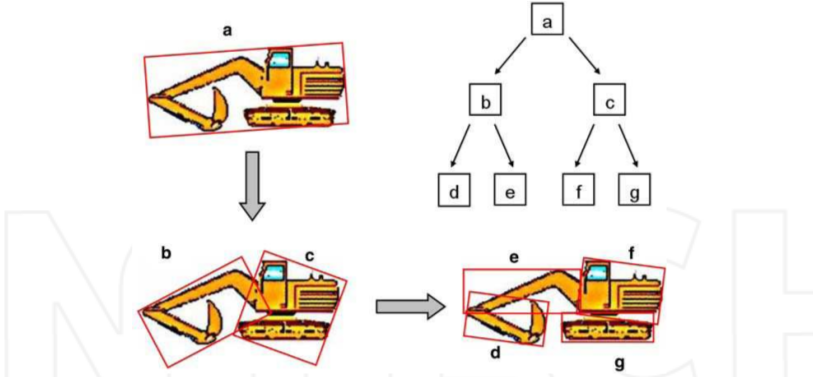
Figure 5. Tree of objects.

The use of such trees is necessary to reduce the number of calculations.
Obviously, if checking for collisions is carried out directly at the sites, it may take too much time. The use of limiting volumes makes this task a little easier. And the combination of limiting volumes into a hierarchical system makes it possible to exclude the obviously non-intersecting parts of the object.

Usually a tree is created in one of three ways.

A complex object (rutovy node) is divided into less complex (child nodes). For example, until the objects run out or until some condition is fulfilled. (top down method)

Simple objects (nodes) are combined into more complex ones until there remains one complex root object (bottom up method).

Or adding an object to an already-formed tree (insertion method).

With such a balanced tree, the search complexity is equal to the complexity of other balanced binary search trees - O (logN).

The most interesting question is how to divide an object into children.
The criterion for comparing parts of an object to be placed in the left or right subtree may differ.

The simplest is a simple division of the space in half: all objects with coordinates above a certain point go to the right subtree, all the rest go to the left.

There can also be a calculation of the average value, for example, along the selected axis.
Or building a median. Or in any other way.


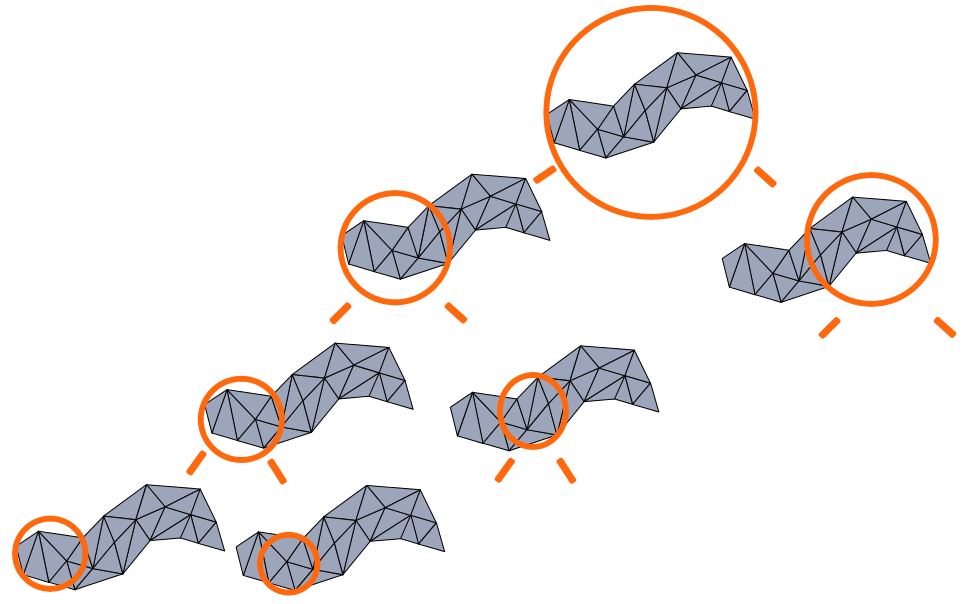
Figure 6. Another abstract tree of objects.

Collision search

The search for collisions on two hierarchical structures, in turn, can also be implemented in different ways.

To check for the intersection of two objects, you simply need to create a tree (BVH-tree) for each object, where the node determines its part of the object through some limiting volume.

Next, you need to walk through the trees and compare the node from one tree with the nodes of another, so as to move only in the direction where there is an intersection of their limiting volumes.


Figure 7. Recursion tree of object mapping.

Illustrations and Information

1. Christer Ericson. Real-Time Collision Detection, Volume 1. - A triangle and a useful paragraph about polyhedra.
2. Hamzah Asyrani Sulaiman and Abdullah Bade. Bounding Volume Hierarchies for Collision Detection. - Excavator, bunny and quite simply about collisions, hierarchies.
3. Johannes Mezger. Collision Handling in Dynamic Simulation Environments: Bounding Volume Hierarchies. - Tree and polyhedron intervals. Briefly and briefly about the main issues of hierarchical structures of limiting volumes.
4. Rolf Lakaemper. Game Programming. Introduction To Collision Detection - Title zvlekalovo and masterpiece with men. A simple overview on the definition of collisions.
5. An example of a simple implementation of the search for intersections or collisions using a BVH tree and discrete-oriented polyhedra.