Arbelos

Download the article as a Mathematica document (NB) , CDF file or PDF .
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

This article systematically checks some properties of a figure known since ancient times, called Arbelos . It includes several new discoveries and generalizations presented by the author of this work.

Introduction

Being motivated by the computational advantages that Mathematica has, some time ago I decided to start researching the properties of arbelos, a very interesting geometric figure. Since then, I have been impressed with the large number of amazing discoveries and computational problems that have arisen because of the ever-expanding amount of literature relating to this remarkable object. I recall its resemblance to the lower part of the penny-farthing cult bike from The Prisoner (1960s TV series), the Punch and Judy jesterly hat and the Yin-Yang symbol with one inverted arc; see fig. 1. Currently there is a specialized catalog of Archimedean circles (circles contained in Arbelos) [1] and important applications of the properties of Arbelos that lie outside the field of mathematics and computational sciences [2].

Many well-known researchers were engaged in this topic, including Archimedes (killed by a Roman soldier in 212 BC), Papp (320 AD), Christian O. Mor (1835-1918), Victor Tebo ( 1882-1960), Leon Bancoff (1908-1997), Martin Gardner (1914-2010). For quite some time now, Clayton Dodge, Peter Ay. Wu, Thomas Schoch, Hiroshi Okumura, Masayuki Watanabe and others.
')
Leon Bancoff is a man who has attracted widespread attention to arbelos in the past 30 years. Schokh attracted the attention of Bancoff to Arbelos in 1979, opening several new Archimedean circles. He sent a 20-page manuscript to Martin Gardner, who sent it to Banckoff, who then sent a 10-page fragment of a copy of the manuscript to Dodge in 1996. Due to the death of Benkoff, the planned collaboration was interrupted until Dodge reported on some new discoveries [3]. In 1999, Dodge said that it would take him from five to ten years to sort out all the material he has, putting the whole thing into pieces. This work is still ongoing. Not surprisingly, in the fourth volume of The Art of Computer Programming , it is said that important work requires a lot of time.


Fig. 1. Penny-farthing bicycle, Punch and Judy dolls, physical arbelos.

Arbelos (“shoemaker's knife” in Greek) is so named because of its similarity to the blade used by shoemakers (Fig. 1). Arbelos is a flat region bounded by three semi-circles and a common base line (Fig. 2). Archimedes was probably the first to start studying the mathematical properties of Arbelos. These properties are described in theorems 4 through 8 of his book Liber assumptorum (or the Book of Lemmas ). Perhaps this work was not written by Archimedes. Doubts appeared after a translation from the Arabic Book of Lemmas , in which Archimedes is mentioned repeatedly, but nothing is said about his authorship (however, there is an opinion that this book is a fake [4]). The book of Lemmas also contains the famous Archimedean Problema Bovinum [5].

This article is aimed at the systematic presentation of some properties of Arbelos and is not exhaustive. Our goal is to develop a uniform computational methodology in order to present these properties in the format of a training article. All properties are built within a certain sequence and presented with evidence. These proofs were implemented by testing equivalent calculated statements. In the course of this work, the author made several discoveries and made several generalizations.

We call the largest semicircle the upper arc , and the two smaller ones, the left-sided and right-sided arcs , or simply the side arcs , if there is no need to distinguish them. We use and accordingly, to designate their radii, and the radius of the upper arc is denoted as . The segment between two points is non-oriented and extends from one point to another, while a straight line containing two points is infinite and is located outside these two points. Classical inaccuracy in designations - use to designate as the segment itself connecting the points and and its length depending on the context; modern notation tells to write to denote the length of the segment.

This function sets arbelos.



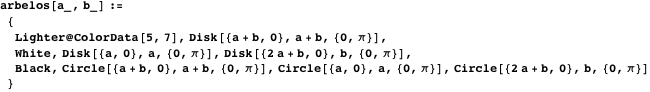
So you can draw Arbelos himself.




Figure 2. Arbelos.

Property 1
The perimeter of the arbelos is equal to the perimeter of the largest circle.

Property 2
The area of ​​arbelos is equal to the area of ​​a circle with a diameter .

This is lemma number 4 of the Book of Lemmas (Fig. 3) [7, 8].

These two properties are easily proved by calculating the following logical construction, consisting of two equalities.





The drawpoints function displays the set points in red circles.






Fig. 3. The area of ​​the circle diameter (radical circle) is equal to the area of ​​Arbelos.

Radical circle

Circle on ris. 3 is called the radical circle of arbelos, and the line is called its radical axis (this terminology will be explained in Generalizations ). Denote and name the points, lines, circles and coordinates that we need to illustrate properties 3-11 and 25-26 (Fig. 4).




Fig. 4. Designations of coordinates, lines and circles mentioned in properties 3-11 and 25-26.

Property 3
Lines and perpendicular and intersect lateral arcs at points and connecting to a common tangent to the side arcs.

To prove perpendicular lines and calculate the scalar product of vectors and .





Use the obtained result to obtain the angle of the straight line .

Theorem 1
The equation of the tangent to the left arc at the point :



and the equation is tangent to the right arc at the point :



The PQ function finds the coordinates of the touch points. and by solving a system of four equations that specify their positions on the arcs and the angles of inclination of the tangents according to Theorem 1.

In addition to PQ , this article also includes the following notation for points and quantities: VWS , HK , U , EF , IJr, and LM .

The dSq function calculates the square of the distance between two given points.









Property 4
Points and are on a radical circle.

Because is the diameter of a radical circle, we only need to prove the equality of the distances from and to the center of the radical circle, which is denoted as .





Property 5
Let line intersects the upper arc at points and . Then and lie on a circle with center in and radius .

We get the coordinates of the points and , solving a system of equations that specifies their location on the upper arc and on the line .







This proves property 5 by checking that the distances from and before equal distance from before .





Property 6
Straight parallel straight .

This is equivalent to the fact that the determinant of vectors and (their vector product) is equal to zero.





Property 7
Straight perpendicular straight .

This is equivalent to the scalar product of vectors and equals zero.





Denote the circle centered at and radius as .

Property 8
Couples , and , - are pairs of mutually reverse points for a circle .

Back point to point in circumference (wherein ) is such a point that equality holds [9]. The inversion function implements this idea.



So you can prove property 8 by substituting instead .





Property 9
Investigate the circle of reverse points . For a given point circle , , match their inverse points. Section is reverse for arc and cut - arc inversion . Dougie and are also reciprocal. The radical circle is the inversion of a straight line. .

Property 10
Straight lines and there are tangents to the radical circle.

This statement is analogous to the fact that the corresponding arcs (that is, their tangent) are perpendicular to the radical circle (its tangent at the intersection points). According to property 8 , arcs are perpendicular to a circle with a diameter if they pass through a pair of reverse points [10,11].

Property 11
- a rectangle.

This is one of the surprises of Bankoff's surprises [12,13,14]. If all four points lie on a radical circle, it suffices to prove that halves .





The following slider demonstration (implemented through the Manipulate function) illustrates properties 3-11. The easiest way to specify the points P , Q , H , K is to copy and paste the corresponding formulas for them.

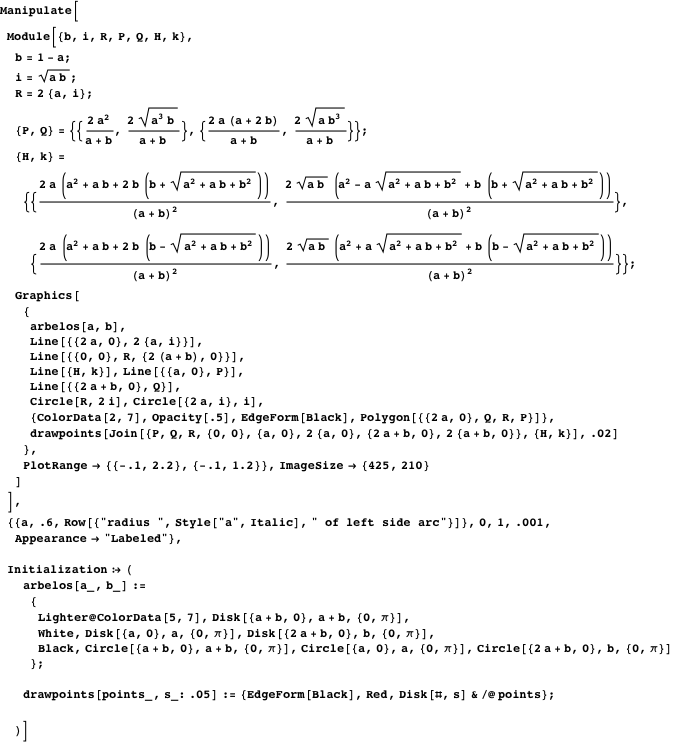
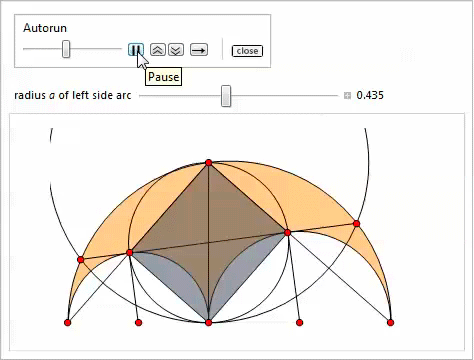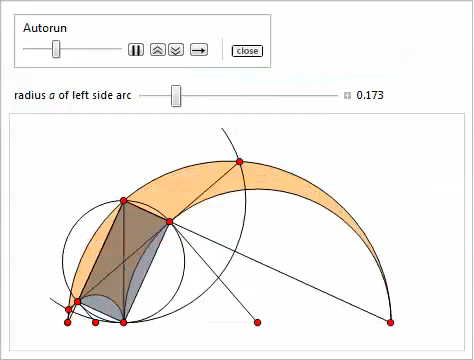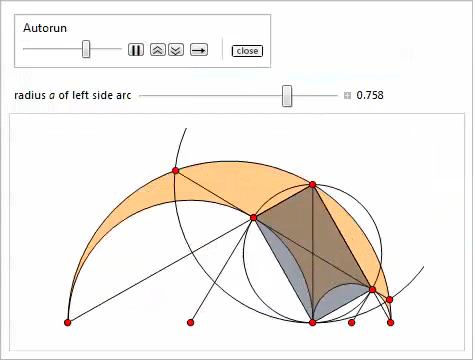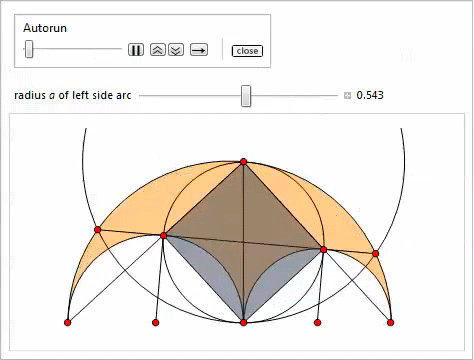
Inscribed circle

Now consider the circle tangent to the side arcs and the top arc - the inscribed circle in arbelos with touch points , and (see fig. 5) [15, 16]. We also denote the vertices of the arcs by dots. and respectively.




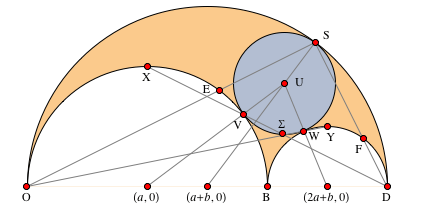
Fig. 5. The inscribed circle , coordinates, lines and points shown in the figure appear in properties 12 through 15.

The sixth statement from the Book of Lemmas also includes the radius of the inscribed circle, denoted as . U function calculates center coordinates inscribed circle and its radius .







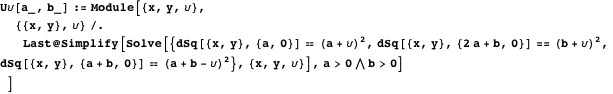
Coordinates of touch points , and determined by the intersection of the lines connecting the centers of the arbelos arcs with the inscribed circle.







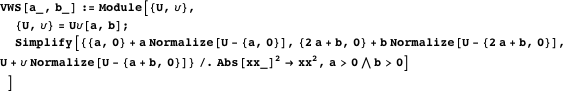
Property 12
Points , and lie on one straight line. Points , and lie on one straight line. Lines and intersect at a point which lies on the inscribed circle.

The first two statements can be proved using the criterion of the determinant to check collinearity.





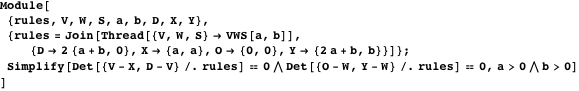
Let be will be the point of intersection of the lines and . Proving that the distance from this point to equally , we prove the third statement.





Property 13
Points , , and lie on a circle centered in . Similarly, points , , and lie on a circle centered in .









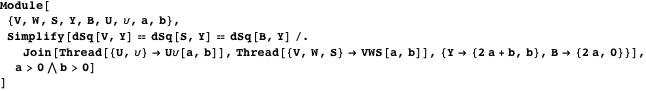
The following demo with Manipulate illustrates property 13 [17]. The Bankoff circle option will show the inscribed circle in the triangle that connects the centers of the arcs. This illustrates property 23.





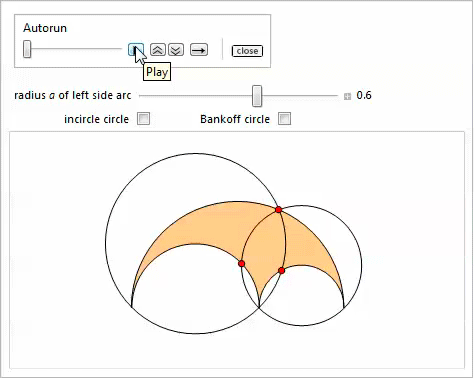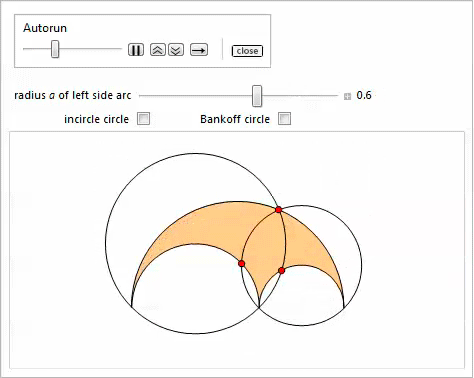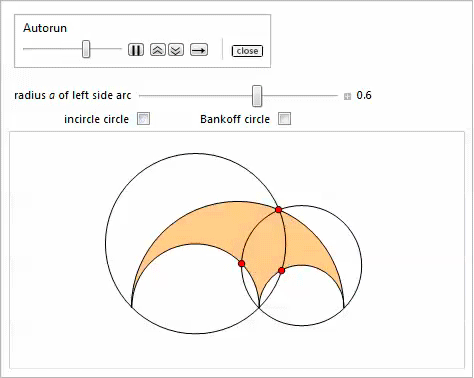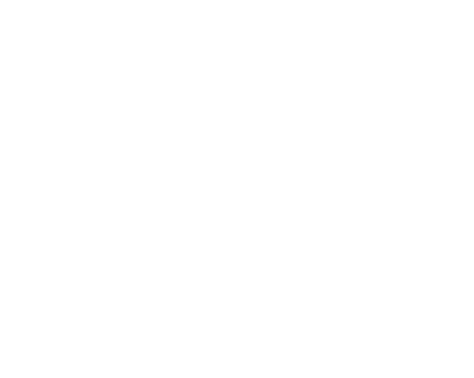
Property 14
Let be - diameter of the inscribed circle, parallel , but - projection on . Rectangle between segments and - square.

This property is illustrated in the following demonstration with Manipulate and can be easily tested with the following expression.





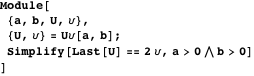
Property 15
Let be and - crossing lines and with side arcs. Then - the square is almost the same size as the square, which was mentioned in property 14.

First get the points and as the intersection of the corresponding lines and arcs, and then store the result in the replaceEF variable.







We prove property 15 by making equal to the vector obtained by rotation around by 90 ° and making equal to the vector obtained by moving through .





Considering and The following graph compares the sizes of two squares.





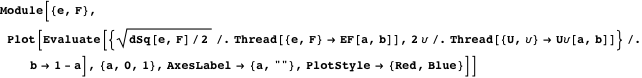
A demo with Manipulate illustrates properties 14 and 15.

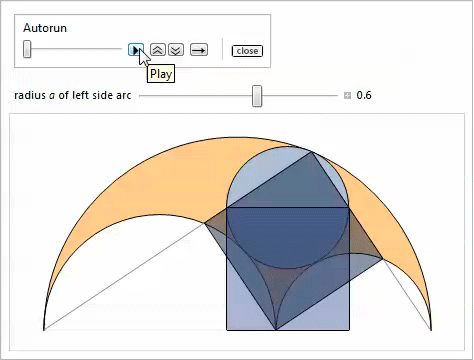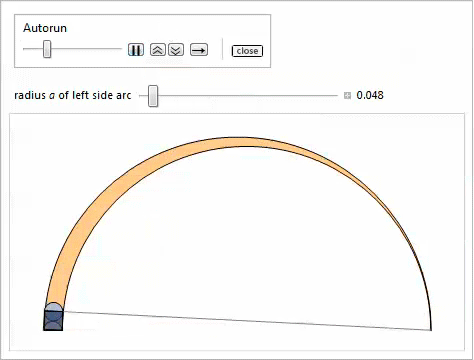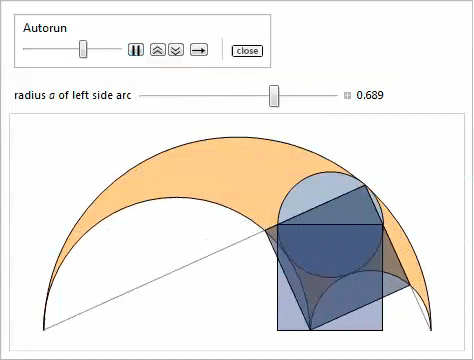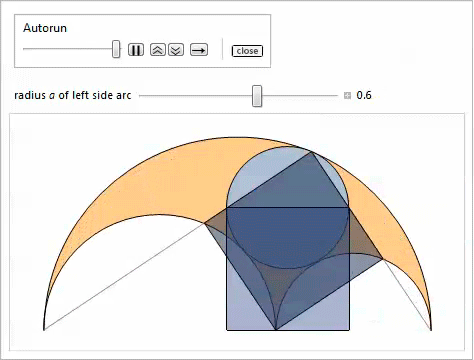
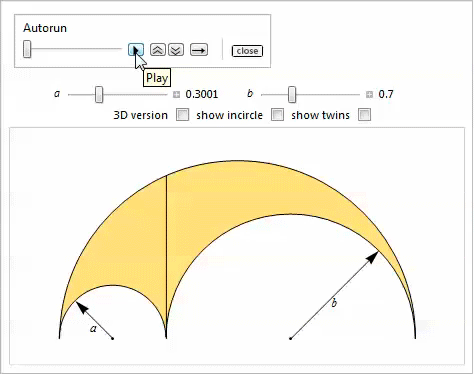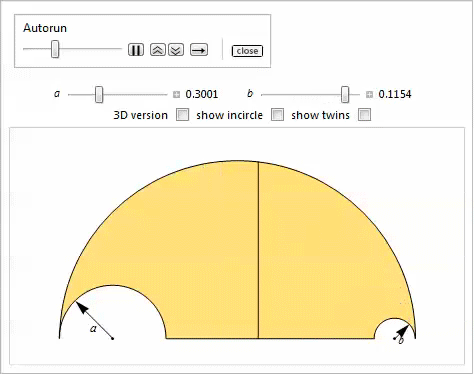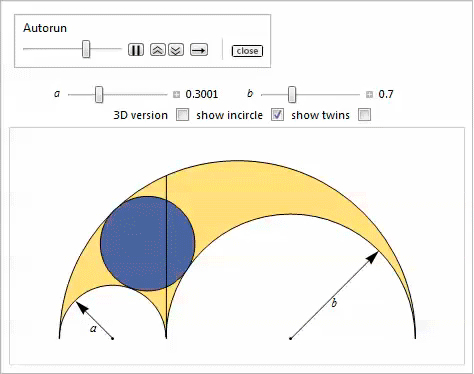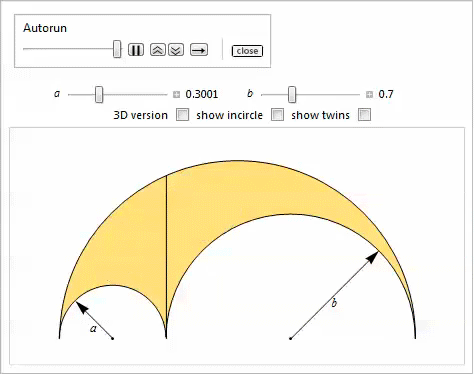
Twins

Consider two gray circles that touch the radical axis, as well as the side and top arcs in fig. 6. They are called twins , or Archimedean circles . In connection with the following remarkable property, they have been well studied. Many of their unusual features were highlighted in our property list [3, 18, 19].




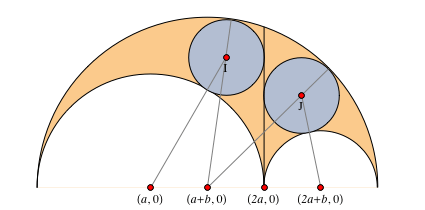
Fig. 6. Twins.

Property 16
Two circles that are tangent to the radical axis, the upper and side arcs of Arbelos, have the same radius.

This property goes as the fifth statement in the Book of Lemmas . Solving this system of six equations, we find the values ​​of their radii, check that they are equal and find the coordinates of their centers. , .





These four solutions give centers grouped in pairs: , , , Where and are mappings and on the diameter of arbelos; Only the last expression is valid. It also shows that the twins are really the same radius. . Any circle whose radius has the same length as that of the twins is called Archimedean . You can draw a pretty visual analogy for if you imagine that and - (electrical) resistance. Then - resistance obtained by parallel connection and ; i.e . The IJr function calculates the coordinates of the centers and the length of the twins' radius.



Property 17
The area of ​​arbelos is equal to the area of ​​the smallest circle that covers the twins.

Consider a circle tangent to both twins, centered at and radius . Then we will have two possible values ​​for .







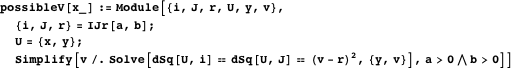
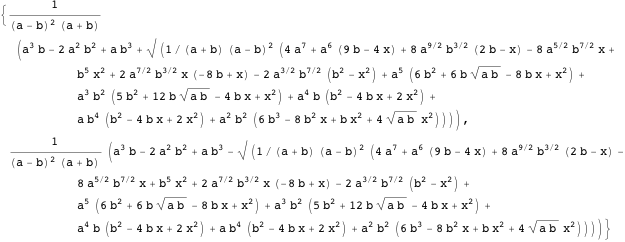
To find the extremum for , equate the derivatives of both equations to zero and solve them with respect to .





Thus, the centers of the smallest and largest circles tangent to the twins lie on the radical axis. Moreover, their centers lie at one point, which follows from the solution of this expression.





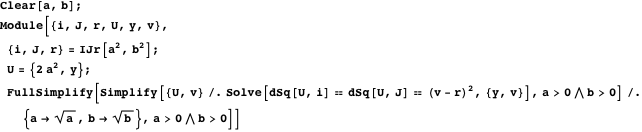
Thus, using property 2, we prove that the greatest tangent circle, which is the smallest of those containing twins, satisfies property 17. The following demonstration with Manipulate shows circles tangent to twins, while you can adjust the radius left side arc.





The following graph compares the radii of two circles tangent to the twins with the centers on the radical axis.








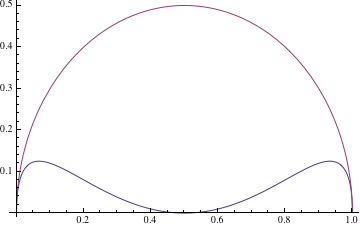
Fig. 7. Designations of points and segments, which will appear in properties 18-24.

Property 18
The common tangent to the left arc and the twin (the touch point is ) passes through the point . Similarly, the common tangent to the right arc and the twin (the point of tangency is ) passes through the point (see fig. 7).

So you can calculate the touch points and .







Using Theorem 1, we prove both statements.





Property 19
Length equal to length . Length equal to length .

We prove both statements at the same time.





However, the points , and don't lie on a circle centered in as well as points , and don't lie on a circle centered in ; otherwise, the following expression would be zero.





Property 20
Line divides the segment in half. Line divides the segment in half.

Since the length of the segment - ordinate and the length of the segment - ordinate , it is enough to check that the centers of these segments lie on the indicated lines by checking the inclination angles.





Property 21
Two blue circles with diameters on going through and tangents to and are archimedean.

These circles are the fourth and fifth Archimedean circles, opened by Bancoff [20]. To check this property, use the following result [21]:

Theorem 2
Distance from point to the straight line passing through the points and there is:



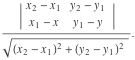
This oriented distance will be positive if the triangle intersects counterclockwise, and negative otherwise. This mapping is implemented by the dAB function.



Let be and - respectively, the center and radius of the blue circle on the left side of the point (Fig. 7). Solving the following system, we find the value .





Similarly, you can calculate the radius of the blue circle to the right of which equals .





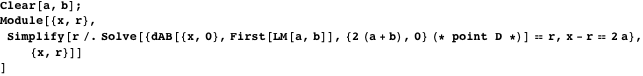
Thus, both circles are Archimedean, as was said earlier. The next demo with Manipulate contains twins and two other circles.





Property 22
Circle passing through points , and in fig. 5, which is called the Bankoff circle - is an Archimedean circle.

Archimedes discovered the original two twins; Bankoff added them with a third circle, opened in 1950 [22]. Center coordinates Benkoff’s circles can be obtained by calculating the distances from to points , and .





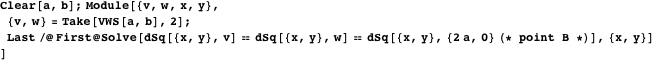
Property 23
Bancoff circle - inscribed in a triangle, which is formed by connecting the centers of the side arcs and the center inscribed in arbelos circle.

Using Theorem 2 to calculate the distance from to the sides of the triangle, we prove this property (since dAB calculates the oriented distance, the order of the arguments describing the line is very important).





Property 24
Circle tangent to circles , and the upper arc - Archimedean.

Thus it is possible to calculate the values and .





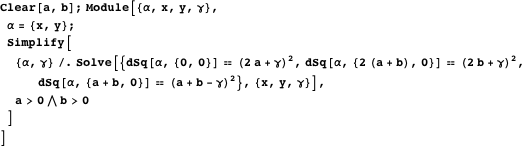
Circle - the only one for which the ordinate - positive. It should be noted that - not a radical axis.





Property 25
Circumference and tangent to the radical axis and passing through and respectively, are Archimedean (see Fig. 4).





Property 26

Circle tangent to a straight line and the upper arc at the point - Archimedean (see Fig. 4).

Circle with center at point and radius tangent to such that distance from before equally , and the equation takes the following form:



Since the circle passes through ,



Since the circle tangent to the upper arc,



Here we use explicit expressions for , and which satisfy these three equalities.





Property 27
Consider two segments (marked in red) connecting the center of the upper arc with the vertices of the left and right arbelos arc. These segments are equal and perpendicular. Tangent circles and in points and to these segments and the upper arc are the Archimedes (see Fig. 8).

This property was discovered in the summer of 1998 [23].




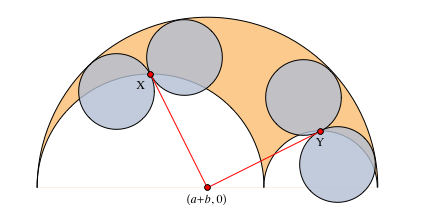
Fig. 8. Two pairs of Archimedean circles from property 27.

Inclined twins

It was shown that there are Archimedean circles distinct from the twins, namely, the Benckoff circles, which appear in properties 21-27. There are also non-Archimedean twins - pairs of circles with the same radius, different from the radius of the twins, which appear in certain areas of arbelos.

The discovery of inclined twins arose from the assumption that in addition to touching the side and top arcs, the twin circles can touch each other, and it is not necessary to touch the radical axis.

Obviously, there are an infinite number of solutions if we do not require that these circles be of the same radius. The idea was as follows: if we start with the assumption that they are of equal radius, we might as a result find that they touch the radical axis. It turned out to be wrong. Consider circles with centers at points. and and with the same radius . Value can be obtained by solving a system of five equations.





These expressions include square roots that differ in sign. Positive roots diverge by and deviate.





The rest - converge.





To sum up: the inclined twins are really equal and their total radius equals



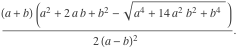
The following comparison between the radii of ordinary and oblique twins shows that they differ very little.





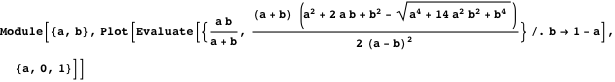
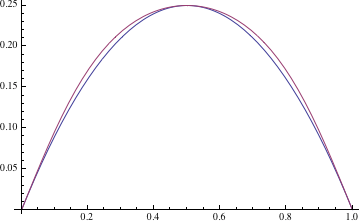
So you can get the coordinates of the centers of the inclined twins.







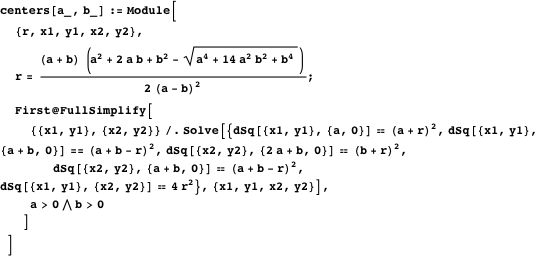
The following demonstration with Manipulate shows oblique twins and, optionally, twins, which are obtained by changing the parameter .

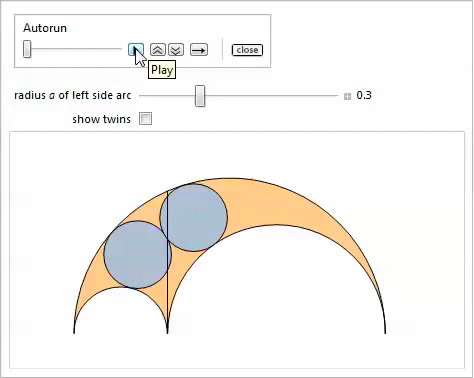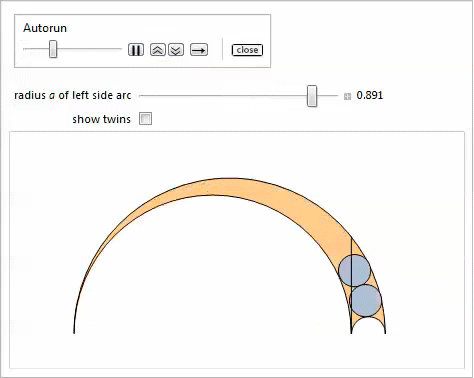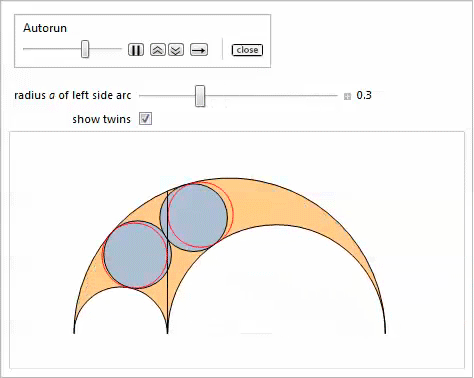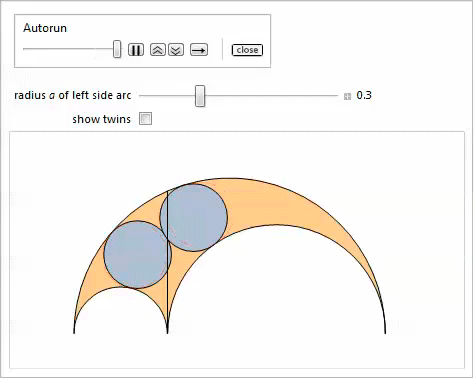
Generalizations

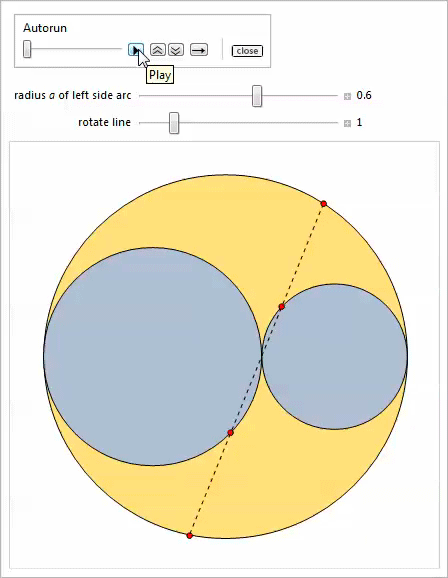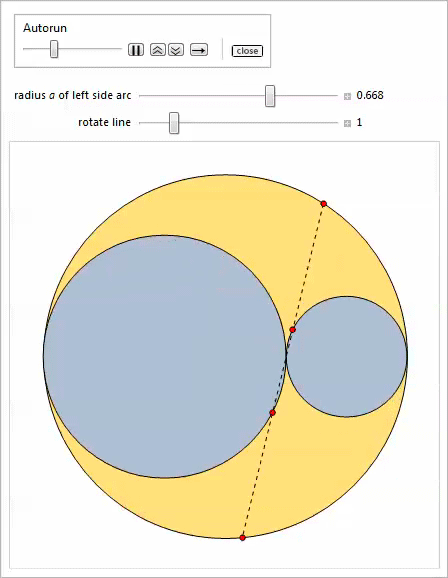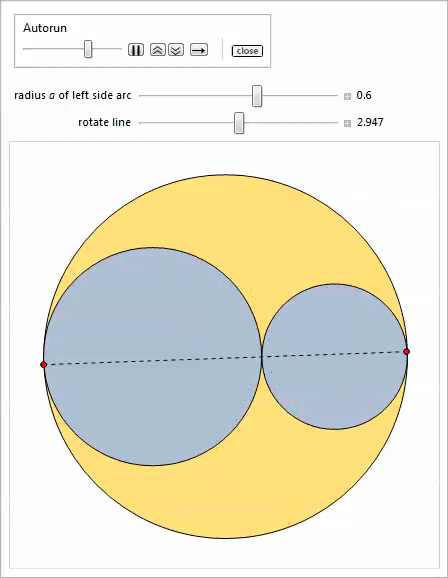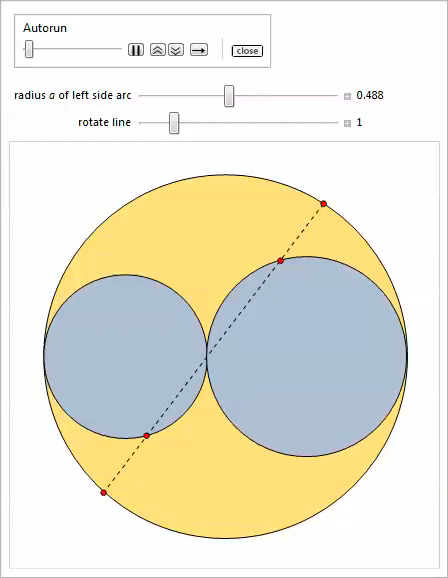
In this section, we generalize the geometry of Arbelos, allowing the arcs to intersect and considering the three-dimensional version. To set the context of the first of the generalizations, we introduce the concept of a radical axis for two circles .

Radical axis

Let be - point, and - circle . Degree of relationship to determined by some property number . Power positive, zero or negative when positioned , , [12]. Let be ; , , , , . , , , , : , .

. . , and . , . .

Manipulate , , .





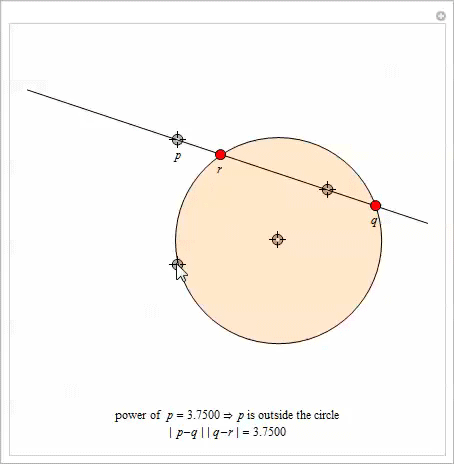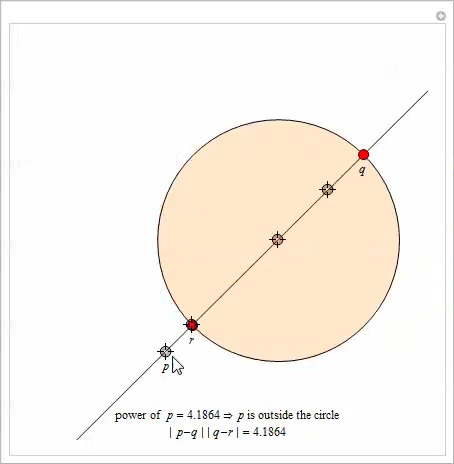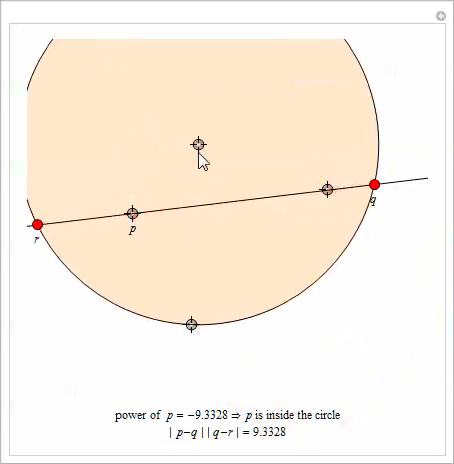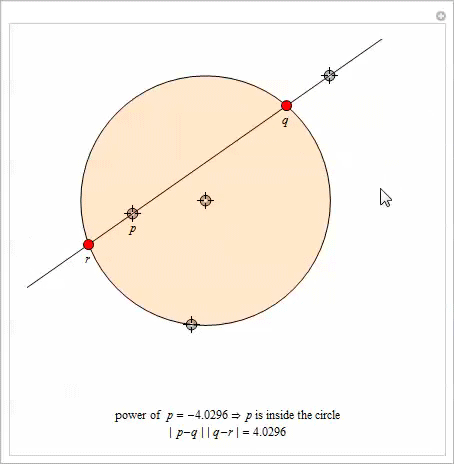
. , , . [10].

3
and , . , .

1
, . .

4
, .

Manipulate ; , , , . 4.

.





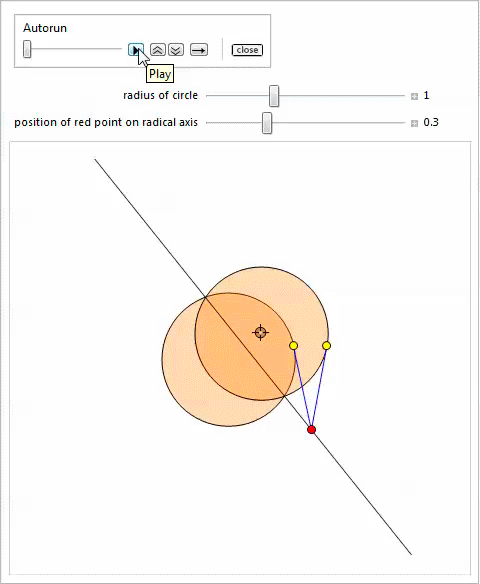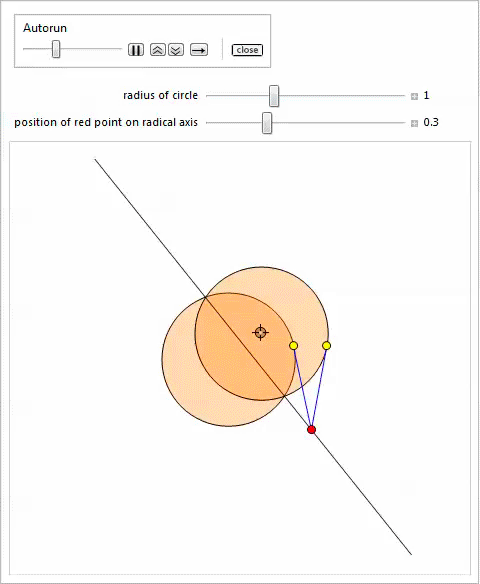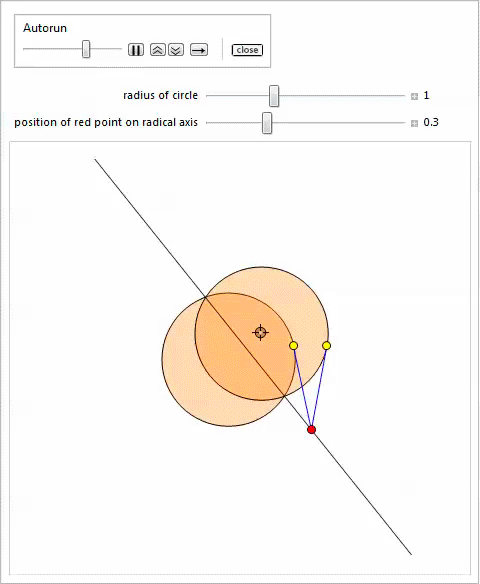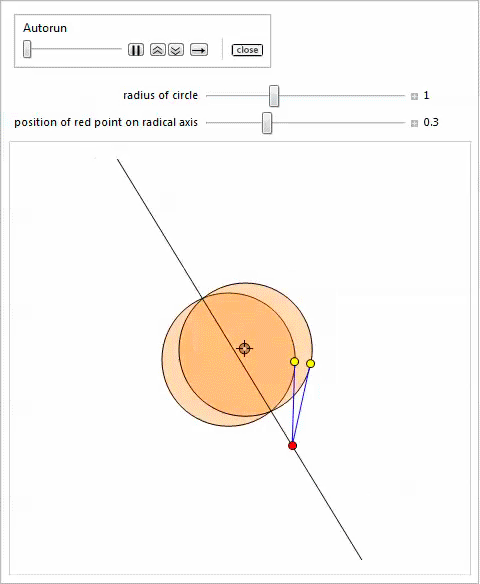
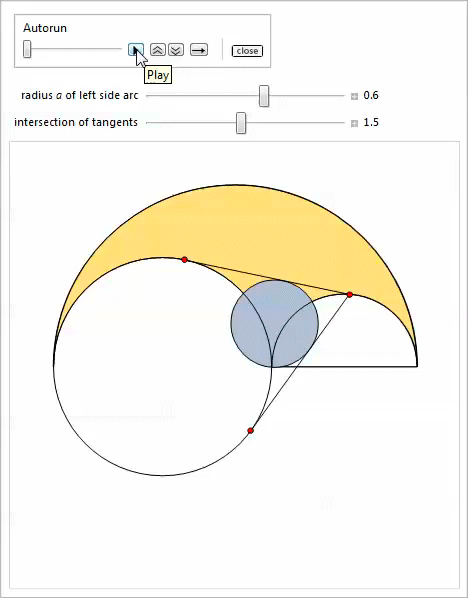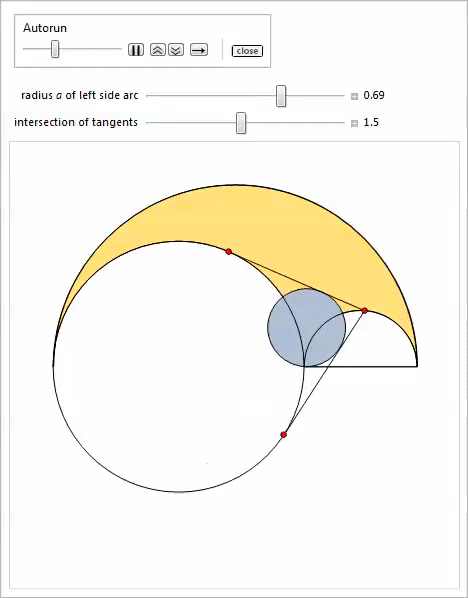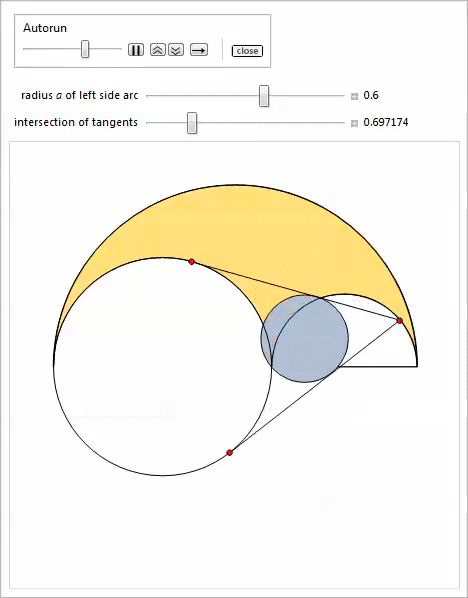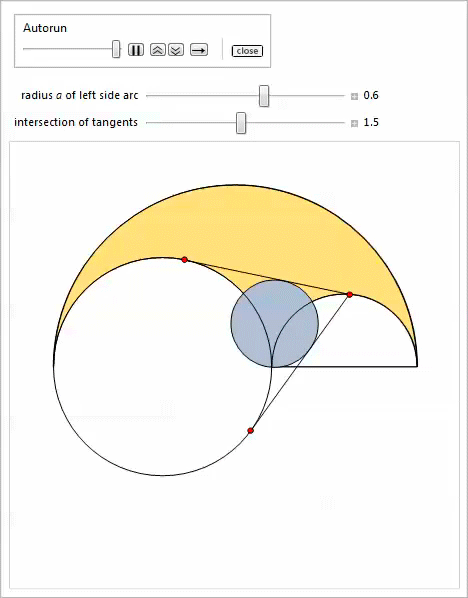
28
, .

Let be — ( ) — , , [10].

5
and , , .

, .





, , , and ( ). and . .





, , .

, . , , , [24,25].

Manipulate .





Manipulate .





, Manipulate .

Bibliography

[1] F. van Lamoen. “Online Catalogue of Archimedean Circles.” (Jan 22, 2014) home.planet.nl/~lamoen/wiskunde/arbelos/Catalogue.htm .

[2] S. Garcia Diethelm. “Planar Stress Rotation” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/PlanarStressRotation .

[3] CW Dodge, T. Schoch, PY Woo, and P. Yiu, “Those Ubiquitous Archimedean Circles,” Mathematica l Magazine, 72 (3), 1999 pp. 202-213. www.jstor.org/stable/2690883 .

[4] HP Boas, “Reflection on the Arbelos,” American Mathematical Monthly , 113 (3), 2006 pp. 236-249.

[5] HD Dörrie, 100 Great Problems of Elementary Mathematics: Their History and Solution (D. Antin, trans.), New York: Dover Publications, 1965.

[6] J. Rangel-Mondragón. “Recursive Exercises II: A Paradox” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/RecursiveExercisesIIAParadox .

[7] RB Nelsen, “Proof without Words: The Area of an Arbelos,” Mathematics Magazine , 75 (2), 2002 p. 144.

[8] A. Gadalla. “Area of the Arbelos” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/AreaOfTheArbelos .

[9] J. Rangel-Mondragón, “Selected Themes in Computational Non-Euclidean Geometry. Part 1. Basic Properties of Inversive Geometry,” The Mathematica Journal , 2013 . www.mathematica-journal.com/2013/07/selected-themes-in-computational-non-euclidean-geometry-part-1 .

[10] D. Pedoe, Geometry: A Comprehensive Course , New York: Dover, 1970.

[11] M. Schreiber. “Orthogonal Circle Inversion” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/OrthogonalCircleInversion .

[12] MG Welch, “The Arbelos,” Master's thesis, Department of Mathematics, University of Kansas, 1949.

[13] L. Bankoff, “The Marvelous Arbelos,” The Lighter Side of Mathematics (RK Guy and RE Woodrow, eds.), Washington, DC: Mathematical Association of America, 1994.

[14] GL Alexanderson, “A Conversation with Leon Bankoff,” The College Mathematics Journal , 23 (2),1992 pp. 98-117.

[15] S. Kabai. “Tangent Circle and Arbelos” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TangentCircleAndArbelos .

[16] G. Markowsky and C. Wolfram. “Theorem of the Owl's Eyes” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TheoremOfTheOwlsEyes .

[17] PY Woo, “Simple Constructions of the Incircle of an Arbelos,” Forum Geometricorum , 1 , 2001 pp. 133-136. forumgeom.fau.edu/FG2001volume1/FG200119.pdf .

[18] B. Alpert. “Archimedes' Twin Circles in an Arbelos” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ArchimedesTwinCirclesInAnArbelos .

[19] J. Rangel-Mondragón. “Twins of Arbelos and Circles of a Triangle” from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TwinsOfArbelosAndCirclesOfATriangle .

[20] H. Okumura, “More on Twin Circles of the Skewed Arbelos,” Forum Geometricorum , 11 , 2011 pp. 139-144. forumgeom.fau.edu/FG2011volume11/FG201114.pdf .

[21] EW Weisstein. “Point-Line Distance—2-Dimensional” from Wolfram MathWorld —A Wolfram Web Resource. mathworld.wolfram.com/Point-LineDistance2-Dimensional.html .

[22] L. Bankoff, “Are the Twin Circles of Archimedes Really Twins?,” Mathematics Magazine , 47 (4), 1974 pp. 214-218.

[23] F. Power, “Some More Archimedean Circles in the Arbelos,” Forum Geometricorum , 5 , 2005 pp. 133-134. forumgeom.fau.edu/FG2005volume5/FG200517.pdf .

[24] AV Akopyan, Geometry in Figures , CreateSpace Independent Publishing Platform, 2011.

[25] H. Okumura and M. Watanabe, “Characterizations of an Infinite Set of Archimedean Circles,” Forum Geometricorum , 7 , 2007 pp. 121-123. forumgeom.fau.edu/FG2007volume7/FG200716.pdf .