Software renderer - 2: rasterization and attribute interpolation
Hey. In the last article I described the mathematics, which is necessary to display a three-dimensional scene on the screen in the form of a grid — we stopped at the moment of obtaining the coordinates of the vertices in the space of the screen. The next step is to “fill” the polygons of which the object consists, i.e. Search for pixels that are included in the image of an object on the screen. The process of finding these points is called rasterization. We also want to be able to texturize and illuminate objects — to do this you need to be able to interpolate the attributes specified in the vertices (for example, texture coordinates, normals, color, and others).
Our input data is a set of polygons (we will only consider triangles): the coordinates of their vertices (the coordinate system depends on the algorithm) and the values of the attributes in each of these vertices, which will later be interpolated along the surface of the triangle. There are several pitfalls that I will discuss in this article:
I will consider three approaches to rasterization:
Also at the end there will be a link to the project, which is an example of implementation, and there will also be code examples from there.
So, rasterization is the process of searching for pixels that are “included” in a given polygon. For a start, we will assume that it is enough for us to fill the polygon with a solid color - nothing superfluous.
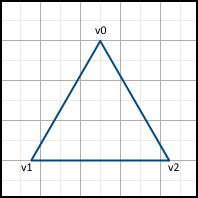
Imagine that we have the following triangle to display on the screen (all coordinates are already represented in screen space):
')

What pixels need to paint over? A pixel can be entirely outside the polygon, partially in the polygon and entirely in the polygon:
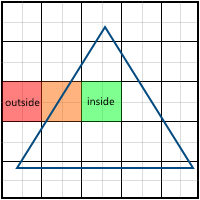
Everything is simple for two cases:
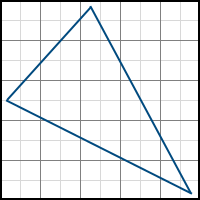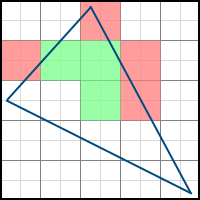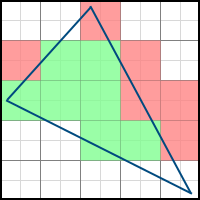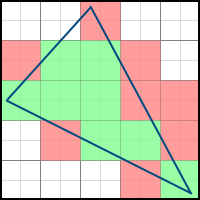
The third case (the pixel is partially inside the polygon) is more complicated. The first solution that comes to mind is to assume that all such pixels are either included in the polygon or not. But it leads to the wrong result. Three-dimensional models that we are going to draw, consist of a set of triangles, which, in general, should not overlap each other. Overlapping triangles do not make sense, since they only duplicate the already existing information. Thus, many polygons have common faces. The simplest example is a rectangle:
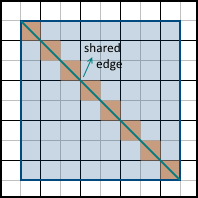
Orange color indicates the pixels that are partially included in both polygons. Now imagine that we rasterize both of these polygons. If we decide that all pixels partially included in the polygon should be filled, we will get the same pixels filled twice (or more if there is a common vertex for more than two polygons). This may not seem like a problem at first glance, but, in fact, it will lead to different artifacts using some techniques, such as alpha blending (drawing using the alpha channel to simulate transparency). It also leads to a decrease in performance, because the number of pixels for which we need to calculate attribute values is increasing. If, on the contrary, we decide that such pixels are not included in the final image and should not be filled, we will get “holes” between polygons, which is unacceptable.
Thus, we came to the understanding that when drawing adjacent polygons each pixel must be filled exactly once. This is a requirement that both Direct3D and OpenGL comply with.
The problem arises because of the need to display from continuous (screen coordinate system) to discrete (pixels on the monitor). The traditional rasterization algorithm (when drawing without smoothing) solves this in the following way: a certain point (sample point) is assigned to each pixel, which is responsible for the pixel's entry into the polygon. Also, it is at this point that the values of all necessary attributes are considered. In other words, all the space occupied by a pixel in the coordinate system of the screen is “represented” by one point. As a rule, this is the center: (0.5, 0.5):

Theoretically, you can take any point inside the pixel, instead of the center. Other values will result in the image being “shifted” by a pixel to one of the sides. Also, in a situation with adjacent polygons, for pixels in which the vertices of the triangles are not located, the use of a point (0.5, 0.5) has a good property: this point enters the polygon that covers more than 50% of the area of the rectangle representing a pixel.
Thus, if the center of a pixel enters a polygon, then it is considered that the pixel belongs to the polygon. But now the following problem arises: what if two polygons have a common face that passes through the center of a pixel? We already understood that a pixel should belong only to one of two triangles, but which one? In the image below, this pixel is marked in red:

This problem is solved by the so-called “filling agreement”.
So, suppose we are faced with the situation described above - two polygons divide the face between each other, which runs exactly through the center of the pixel. Our task is to find out which of the polygons this pixel belongs to.
The de facto standard is the so-called top-left rule: it follows DirectX and most implementations of OpenGL. The essence of this rule is as follows: if a face of a polygon passes through the center of a pixel, then this pixel belongs to the polygon in two cases - if it is the left face or the top face (hence the name).
The concepts of left, right, top and bottom faces require explanation. For now, we will not give exact definitions (we will do this when we get to the traversal algorithms), but we will describe them in a simpler language:
Examples:
Now consider the case of adjacent polygons. If the face is adjacent, and is left in one polygon, then this same edge is right for all polygons that share this edge with this polygon. A similar rule works for the upper and lower edges:

We can use this property to determine which of the adjacent polygons a pixel belongs to. If we agree that a pixel, whose center lies on a common face, belongs only to polygons, in which this face is left, then it will not automatically belong to adjacent polygons, since for them this face is right. And the same for the top face.
In spite of the fact that the rule of the top and left face occurs most often, we can use any suitable combination. For example, the rule of the bottom and left side, top and right, etc. Direct3D obliges to use top-left rule, OpenGL is not so strict and allows you to use any rule that solves the problem of pixel ownership. I will further suggest the use of top-left rule.
Consider the following two polygons:
The second polygon can be obtained from the first as a result of rotation at a certain angle. As a result, some pixels are additionally included in the final image (such pixels are marked in green), and some, on the contrary, disappear from it (marked in red). Accordingly, we need to take into account the fractional parts of the coordinates of the vertices. If we discard them, we get problems when drawing a non-static scene. If, for example, you make the polygon rotate very slowly, then it will do it jerky - because the edges will “jump” sharply from one position to another, instead of correctly processing intermediate results. The difference is easy to understand by comparing these two videos:
Of course, in the case of a static scene, such problems will not arise.
Before proceeding directly to rasterization algorithms, let us dwell on the interpolation of attributes.
An attribute is some information related to an object, which is necessary for its correct drawing according to a given algorithm. Anything can be such an attribute. One of the most frequent options are: color, texture coordinates, normal coordinates. Attribute values are specified at the vertices of the object grid. When rasterizing polygons, these attributes interpolate along the surface of triangles and are used to calculate the color of each of the pixels.
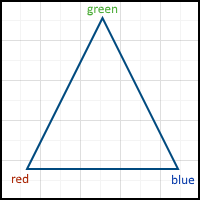
The simplest example (and a kind of analogue of the “hello world”) is the drawing of a triangle, at each vertex of which there is one attribute — the color:
In this case, if we assign a color to each pixel of the polygon, which is the result of linear interpolation of the colors of the three vertices, we will get the following image:
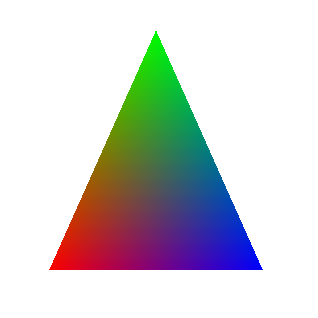
The way in which interpolation is performed depends on the data we use in the drawing process, and they, in turn, depend on the algorithm that is used in rasterization. For example, when using the "standard" algorithm, we can use simple linear interpolation of values between two pixels, and when using traversal-algorithms, barycentric coordinates. Therefore, we postpone it until the description of the algorithms themselves.
Nevertheless, there is another important topic that needs to be addressed in advance: interpolation of attributes with perspective correction.
The easiest way to interpolate is linear interpolation in screen space: after the polygon has been projected onto the projection plane, we interpolate the attributes along the surface of the triangle in a linear fashion. It is important to understand that this interpolation is not correct, since it does not take into account the projection produced.
Consider the projection of the line onto the projection plane d = 1 . At the initial and final vertices are set some attributes that vary linearly in the space of the camera (and in the world). After the projection is made, these attributes do not grow linearly in screen space. If, for example, we take the middle point in camera space ( v = v0 * 0.5 + v1 * 0.5 ), then after the projection this point will not lie in the middle of the projected line:

This is easiest to notice when texturing objects (I will use simple texturing without filtering in the examples below). I have not yet described the texturing process in detail (and this is the topic of a separate article), so for the time being I will limit myself to a brief description.
When texturing at each vertex of the polygon, the attribute value of texture coordinates is specified (it is often called uv by the name of the corresponding axes). These are the normalized coordinates (from 0 to 1 ) that determine which part of the texture will be used.
Now imagine that we want to draw a textured rectangle and set the four values of the uv attribute so that the texture is used entirely:

It seems that everything is not bad:

However, this model is parallel to the projection plane, and therefore there should be no distortion due to the perspective. Let's try to move the top two vertices by one along the z axis, and the problem will be immediately visible:

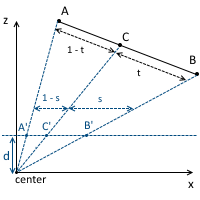
Thus, it is necessary to consider the perspective when interpolating attributes. The key fact to this is that, although z cannot be correctly interpolated in screen space, 1 / z - it can. Consider the line projection again:
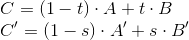
We also already know that along similar triangles:

Interpolating x in screen space, we get:

Interpolating x in camera space, we get:

These three equations are key and all subsequent formulas are derived from them. I will not give a complete conclusion, since it is easy to do this on my own, and I will describe it only briefly, focusing on the results.
Substituting these two equalities into the equation obtained from the ratios of the sides of the triangle, and simplifying all the expressions, we end up with the fact that the inverse of the z- coordinate can be linearly interpolated in screen space:
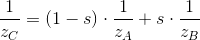
It is important that in this expression interpolation occurs between the values inverse of the z coordinates of the camera space.
Further, suppose that at the vertices A and B the values of a certain attribute are given, we denote them by T1 and T2 , which can also be linearly interpolated in the camera space:
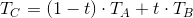
Using intermediate results from the above output, we can write down that the Tc / Zc value can also be correctly interpolated in screen space:

Summarizing, we obtained that 1 / Zc and Tc / Zc can be linearly interpolated in screen space. Now we can easily get the value of Tc :
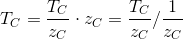
Actually, the cost of prospectively correct interpolation lies mainly in this division. If there is no great need for it, it is better to minimize the number of attributes for which it is used and to do with simple linear interpolation in screen space, if possible. Below is the correct texturing result:

To implement perspective correction, we need values that are inverse to the depth ( z- coordinate) of the vertices in the chamber space. Recall what happens when you multiply by the projection matrix:

Vertices from camera space go to clipping space. In particular, the z- coordinate is subject to certain changes (which will be needed later for the depth buffer) and no longer coincides with the z- coordinate vertex in the camera space, so we cannot use it. And what coincides is the w -coordinate, since we explicitly put z in it from the chamber space (just look at the 4th column of the matrix). In fact, we do not even need z itself, but 1 / z . And we actually get it "for free", because when we go to NDC we divide all the vertices by z (which lies in the w-coordinate):
And, therefore, we can simply replace it with the opposite value:
Below is a description of the three approaches to the rasterization of polygons. Complete code samples will be absent, because a lot of it depends on the implementation, and this will be more confusing than help. At the end of the article there will be a link to the project, and, if necessary, you can see the implementation code in it.
I called this algorithm “standard” because it is the most frequently described rasterization algorithm for software renderers. It is easier to understand than traversal-algorithms and rasterization in homogeneous coordinates, and, accordingly, easier to implement.
So let's start with the triangle that we want to rasterize. Suppose, to begin with, that this is a triangle with a horizontal bottom edge.
The essence of this algorithm is to sequentially move along the side faces and paint over the pixels between them. To do this, first calculate the offset values along the X axis for each offset by one along the Y axis.
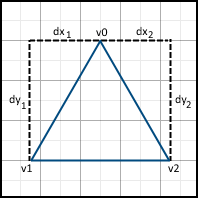
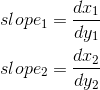
Then, the movement begins along the sides. It is important that the movement starts from the nearest center, and not from the Y- coordinates of the vertex v0 , since the pixels are represented by these points. If the Y coordinate of v0 already lies on the center, then we still move to the next center along this axis, since v0 lies on both the left and the right side, which means this pixel should not be included in the image:
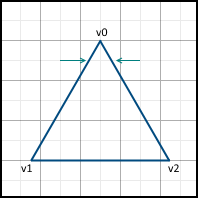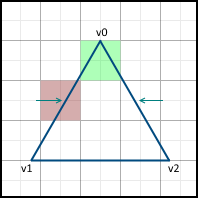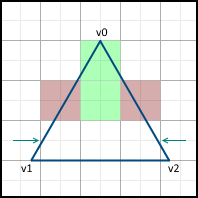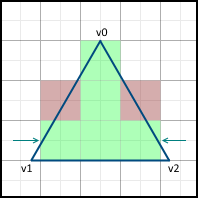
When we move on to the next line, we also start the movement only from the next center along the X axis. If the face passes through the center of the pixel, then on the left side we include the pixel in the image, but not on the right one.
Similarly, the algorithm works for triangles with a horizontal upper side. Those triangles, which do not have a single horizontal side, are simply divided into two triangles - one with the horizontal top and one with the horizontal bottom. To do this, look for the intersection of the horizontal line passing through one of the vertices of the triangle (average along the Y- coordinate), with a different face:

After that, each of these triangles is rasterized according to the algorithm above. It is also necessary to correctly calculate the values of z and w coordinates in the new vertex - for example, interpolate them. Similarly, the presence of this vertex must be taken into account when interpolating attributes.
Interpolation of attributes without perspective correction occurs as follows: when moving along the side faces, we calculate the interpolated attribute values at the start and end points of the line that we are going to rasterize. Then, these values are linearly interpolated along this line. If a perspective correction is needed for an attribute, then instead we interpolate T / z along the edges of the polygon (instead of just interpolating T , the attribute value), as well as 1 / z . Then, these values at the start and end points of the line are interpolated along it and are used to get the total attribute value with perspective, according to the formula given above. It must be remembered that the 1 / z , to which I refer, actually lies in the w-coordinate of the vector after all the transformations produced.
This is a whole group of algorithms using the same approach, based on the equations of the faces of the polygon.
The face equation is the equation of the line on which this face lies. In other words, it is an equation of a line passing through two vertices of a polygon. Accordingly, each triangle is characterized by three linear equations:

To begin with, we describe the equation of a straight line passing through two points (they are the pair of triangle vertices):

We can rewrite it as follows:
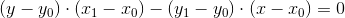

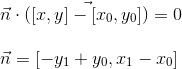
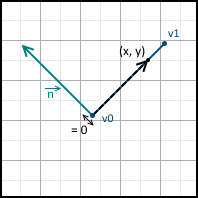
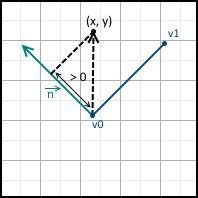
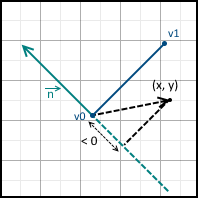
It is clear from the last expression that the vector n is perpendicular to the vector v0 - v1 (the coordinates are reversed, and the X-coordinate is taken with a minus sign). Thus, n is the normal to the line formed by two vertices. This is all the same equation of a straight line, and, therefore, substituting the point (x, y) there and getting a zero, we know that this point lies on a straight line. What about the other values? This is where the normal recording form comes in handy. We know that the scalar product of two vectors calculates the length of the projection of the first vector onto the second, multiplied by the length of the second vector. The first vector is the normal, and the second is the vector from the first vertex to the point (x, y):

And we have three possible options:
They are all shown below:
We can also set the equation of a line so that the normal points in the opposite direction - simply multiplying it by minus one. In the following, I will assume that the equation is composed in such a way that the normal points to the inside of the triangle.
Using these equations, we can define a triangle as the intersection of three positive half-planes.
Thus, the common part of traversal-algorithms is as follows:
Let us dwell on the implementation of top-left rule. Now, when we operate on the normal to the face, we can give more rigorous definitions for the left and top faces:
It is also important to note that the coordinates of the normal coincide with the coefficients a and b in the canonical straight line equation: ax + by + c = 0 .
Below is an example of a function that determines whether a pixel is in the positive half-plane relative to one of the faces (using the top-left rule). It is enough for it to take three arguments per input: the value of the equation of a face at a point, and the coordinates of the normal:
Simple and useful optimization when calculating the values of equations: if we know the value in a pixel with coordinates (x, y) , then to calculate the value at the point (x + 1, y) it is enough to add the value of the coefficient a . Similarly, to calculate the value in (x, y + 1), it suffices to add the coefficient b :
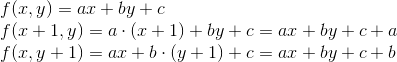
The next step is attribute interpolation and perspective correction. For this, barycentric coordinates are used. These coordinates, in which the point of the triangle is described as a linear combination of vertices (formally, implying that the point is the center of mass of the triangle, with the corresponding weight of the vertices). We will use the normalized version - i.e. the total weight of the three vertices is one:
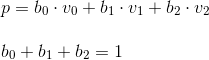
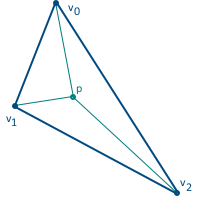
This coordinate system also has a very useful property that allows them to be calculated: the barycentric coordinates are equal to the ratio of the areas of the triangles formed in the figure above to the total area of the triangle (for this reason they are also sometimes called areal coordinates):
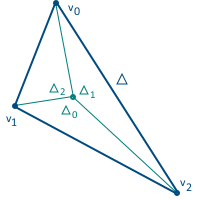
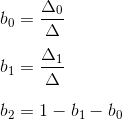
The third coordinate can be calculated not through the areas of triangles, since the sum of the three coordinates is equal to one — in fact, we have only two degrees of freedom.
Now everything is ready for linear interpolation of attributes: the attribute value at a given point of the triangle is equal to the linear combination of barycentric coordinates and attribute values at the corresponding vertices:
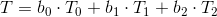
To correct the perspective, we use a different formula — first, we calculate the interpolated T / z value, then the interpolated 1 / z value, and then divide them into each other to get the final T value taking into account the perspective:
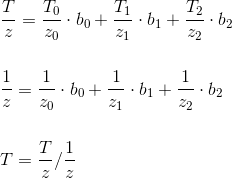
The difference between the different traversal algorithms is how the pixels are selected for verification. We will consider several options.
As the name implies, this algorithm simply builds the axis-aligned bounding box of the polygon, and traverses all the pixels inside it. Example:
This algorithm consists of the following steps:
This can be represented as follows:
It is possible to check that the pixel is to the left of the polygon as follows - at least for one face, for which the normal points to the right (ie, a> 0), the value of the equation for this face is negative.
This algorithm can be considered as an improved version of the backtracking algorithm. Instead of “idle” passing through the pixels in the line, until there is a pixel from which we can begin to move in the right direction, we memorize information about the pixel from which we started moving on the line, and then we pass through the pixels to the left and right of him
This algorithm was originally described in the publication Triangle scan conversion using 2D homogeneous coordinates, Marc Olano & Trey Greer . Its main advantages are the absence of the need for clipping and dividing by the w-coordinate during the transformation of the vertices (with the exception of a couple of reservations - they will be described later).
First of all, suppose that, at the beginning of the rasterization, the x and y coordinates of the vertices contain values that are mapped to coordinates on the screen by simply dividing by the corresponding w- coordinate. This may slightly change the vertex transformation code, provided that several rasterization algorithms are supported, since it does not include division by w-coordinate. Coordinates in a homogeneous two-dimensional space are transmitted directly to the function that produces rasterization.
Let us consider in more detail the question of linear interpolation of attributes along a polygon. Since the value of the attribute (let's call it p ) grows linearly, it must satisfy the following equation (in three-dimensional space):

Since the point (x, y, z) is projected onto the plane using homogeneous coordinates (x, y, w) , where w = z , we can also write this equation in homogeneous coordinates:

Imagine that we know the coefficients a , b and c (we will consider finding them a little later). During rasterization, we deal with the coordinates of pixels in the screen space, which are related to the coordinates in a homogeneous space by the following formula (this was our initial assumption):
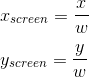
We can express the value of p / w using only coordinates in screen space, by dividing by w:

To get the correct value of p using screen coordinates, we only need to divide this value by 1 / w (or, which is the same, multiply by w ):

1 / w , in turn, can be calculated by a similar algorithm - it is enough to imagine that we have a certain parameter that is the same in all vertices: p = [1 1 1] .
Now consider how we can find the coefficients a , b and c . Since for each attribute its values are given at the vertices of the polygon, we actually have a system of equations of the form:

We can rewrite this system in matrix form:
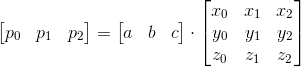
And the solution:

It is important to note that we need to count only one inverse matrix per polygon — then these coefficients can be used to find the correct attribute value at any point on the screen. Also, since we need to calculate the determinant of the matrix to invert it, we get some auxiliary information, because the determinant also calculates the volume of the tetrahedron with vertices at the origin and points of the polygon multiplied by two (this follows from the definition of the mixed product of vectors ). If the determinant is zero, this means that the polygon cannot be drawn, since it is either degenerate, or it is turned edgewise with respect to the camera. Also, the volume of a tetrahedron can be with a plus sign and a minus sign - and this can be used to cut off polygons that are turned "back" to the camera (the so-called backface culling). If we consider the order of the vertices counterclockwise to be correct, then polygons with a positive determinant value should be skipped (provided that the left-side coordinate system is used).
Thus, the question of interpolation of attributes is already resolved - we can calculate the correct value (taking into account the perspective) of any attribute at a given point on the screen. It remains only to decide which points of the screen belongs to the polygon.
Let us recall how the pixel belonging to the polygon was tested in traversal algorithms. We calculated face equations, and then checked their values at the desired point on the screen. If they were all positive (or zero, but belonged to the left or upper edges), then we painted over the pixel. Since we are already able to interpolate attributes along the surface of a triangle, we can use exactly the same approach, considering that we interpolate a certain pseudo-attribute that is zero along the face and some positive value (the most convenient is 1) at the opposite vertex (in fact, this is going through these faces):

Accordingly, the values of these pseudo-attributes for each of the faces:
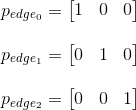
Using them we can calculate the corresponding coefficients a , b and c for each of the faces and get their equations:

Now we can interpolate their values along the surface of a triangle in a similar way and calculate their values at the point we need. If it is positive, or it is zero, but we are on the left and upper edges, the pixel is inside the polygon and must be painted over. We can also apply a small optimization - we do not need the exact values of the equations of the faces at all, its sign is enough. Therefore, dividing by 1 / w can be avoided, we can simply check the signs of p / w and 1 / w - they should be the same.
Since we operate with the same face equation, much of what is said in the section on traversal algorithms can also be applied to this algorithm. For example, top-left rule can be implemented in a similar way, and the values of face equations can be calculated incrementally, which is a useful optimization.
When presenting this algorithm, I wrote that this algorithm does not require the implementation of clipping, since it operates in homogeneous coordinates. This is almost entirely true, except for one case. There may be situations when working with w-coordinates of points that are close to the origin of the coordinates (or coincide with it). In this case, overflow may occur when interpolating attributes. So a good idea would be to add another “face”, which is located parallel to the xy plane and located at a distance of z near from the origin to avoid such errors.
When describing traversal algorithms, I mentioned several options for selecting a set of pixels that should be checked for belonging to a triangle (axis aligned bounding box, backtracking, zigzag algorithms). They can be applied here. This is a situation in which it will still be necessary to divide the vertices by the w-coordinate to calculate the boundary values (for example, the coordinates of the bounding box), we should only provide for situations where w <= 0 . Of course, there are other ways. Passing through all the pixels of the screen is obviously unsuccessful in terms of performance. You can also use tile rasterization, the description of which is beyond the scope of this article.
A project where you can see examples of implementations: github.com/loreglean/lantern . Pull requests with fixes and other things are welcome, it is better to write about errors in the code or questions about it in PM.
Our input data is a set of polygons (we will only consider triangles): the coordinates of their vertices (the coordinate system depends on the algorithm) and the values of the attributes in each of these vertices, which will later be interpolated along the surface of the triangle. There are several pitfalls that I will discuss in this article:
- Pixel Fill Rule
- Accuracy
- Perspective correction with perspective-correct interpolation
I will consider three approaches to rasterization:
- “Standard” algorithm using face tilt
- a number of algorithms based on the use of equations of the polygon (traversal-algorithms)
- uniform rasterization algorithm
Also at the end there will be a link to the project, which is an example of implementation, and there will also be code examples from there.
The basics
So, rasterization is the process of searching for pixels that are “included” in a given polygon. For a start, we will assume that it is enough for us to fill the polygon with a solid color - nothing superfluous.
Imagine that we have the following triangle to display on the screen (all coordinates are already represented in screen space):
')

What pixels need to paint over? A pixel can be entirely outside the polygon, partially in the polygon and entirely in the polygon:

Everything is simple for two cases:
- Pixel is not included in the entire polygon (red color in the picture) - do not paint over
- Pixel enters the entire polygon (green color in the picture) - paint over
The third case (the pixel is partially inside the polygon) is more complicated. The first solution that comes to mind is to assume that all such pixels are either included in the polygon or not. But it leads to the wrong result. Three-dimensional models that we are going to draw, consist of a set of triangles, which, in general, should not overlap each other. Overlapping triangles do not make sense, since they only duplicate the already existing information. Thus, many polygons have common faces. The simplest example is a rectangle:

Orange color indicates the pixels that are partially included in both polygons. Now imagine that we rasterize both of these polygons. If we decide that all pixels partially included in the polygon should be filled, we will get the same pixels filled twice (or more if there is a common vertex for more than two polygons). This may not seem like a problem at first glance, but, in fact, it will lead to different artifacts using some techniques, such as alpha blending (drawing using the alpha channel to simulate transparency). It also leads to a decrease in performance, because the number of pixels for which we need to calculate attribute values is increasing. If, on the contrary, we decide that such pixels are not included in the final image and should not be filled, we will get “holes” between polygons, which is unacceptable.
Thus, we came to the understanding that when drawing adjacent polygons each pixel must be filled exactly once. This is a requirement that both Direct3D and OpenGL comply with.
The problem arises because of the need to display from continuous (screen coordinate system) to discrete (pixels on the monitor). The traditional rasterization algorithm (when drawing without smoothing) solves this in the following way: a certain point (sample point) is assigned to each pixel, which is responsible for the pixel's entry into the polygon. Also, it is at this point that the values of all necessary attributes are considered. In other words, all the space occupied by a pixel in the coordinate system of the screen is “represented” by one point. As a rule, this is the center: (0.5, 0.5):

Theoretically, you can take any point inside the pixel, instead of the center. Other values will result in the image being “shifted” by a pixel to one of the sides. Also, in a situation with adjacent polygons, for pixels in which the vertices of the triangles are not located, the use of a point (0.5, 0.5) has a good property: this point enters the polygon that covers more than 50% of the area of the rectangle representing a pixel.
Thus, if the center of a pixel enters a polygon, then it is considered that the pixel belongs to the polygon. But now the following problem arises: what if two polygons have a common face that passes through the center of a pixel? We already understood that a pixel should belong only to one of two triangles, but which one? In the image below, this pixel is marked in red:

This problem is solved by the so-called “filling agreement”.
Filling Agreement
So, suppose we are faced with the situation described above - two polygons divide the face between each other, which runs exactly through the center of the pixel. Our task is to find out which of the polygons this pixel belongs to.
The de facto standard is the so-called top-left rule: it follows DirectX and most implementations of OpenGL. The essence of this rule is as follows: if a face of a polygon passes through the center of a pixel, then this pixel belongs to the polygon in two cases - if it is the left face or the top face (hence the name).
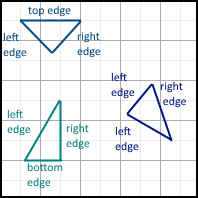
The concepts of left, right, top and bottom faces require explanation. For now, we will not give exact definitions (we will do this when we get to the traversal algorithms), but we will describe them in a simpler language:
- The top face is a horizontal face that is above all other faces.
- Bottom face is a horizontal face that is below all other faces.
- The left side is a face that is located on the left side of the triangle and is not horizontal.
- The right side is a face that is located on the right side of the triangle and is not horizontal.
Examples:

Now consider the case of adjacent polygons. If the face is adjacent, and is left in one polygon, then this same edge is right for all polygons that share this edge with this polygon. A similar rule works for the upper and lower edges:

We can use this property to determine which of the adjacent polygons a pixel belongs to. If we agree that a pixel, whose center lies on a common face, belongs only to polygons, in which this face is left, then it will not automatically belong to adjacent polygons, since for them this face is right. And the same for the top face.
In spite of the fact that the rule of the top and left face occurs most often, we can use any suitable combination. For example, the rule of the bottom and left side, top and right, etc. Direct3D obliges to use top-left rule, OpenGL is not so strict and allows you to use any rule that solves the problem of pixel ownership. I will further suggest the use of top-left rule.
Accuracy
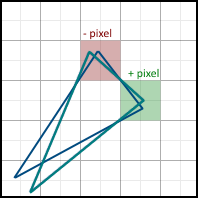
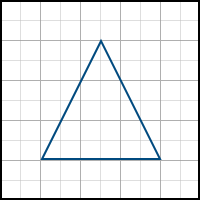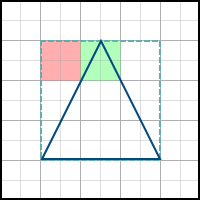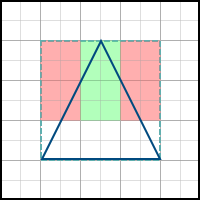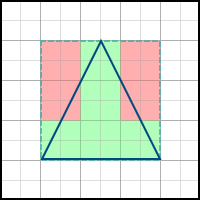
Consider the following two polygons:

The second polygon can be obtained from the first as a result of rotation at a certain angle. As a result, some pixels are additionally included in the final image (such pixels are marked in green), and some, on the contrary, disappear from it (marked in red). Accordingly, we need to take into account the fractional parts of the coordinates of the vertices. If we discard them, we get problems when drawing a non-static scene. If, for example, you make the polygon rotate very slowly, then it will do it jerky - because the edges will “jump” sharply from one position to another, instead of correctly processing intermediate results. The difference is easy to understand by comparing these two videos:
Of course, in the case of a static scene, such problems will not arise.
Attribute Interpolation
Before proceeding directly to rasterization algorithms, let us dwell on the interpolation of attributes.
An attribute is some information related to an object, which is necessary for its correct drawing according to a given algorithm. Anything can be such an attribute. One of the most frequent options are: color, texture coordinates, normal coordinates. Attribute values are specified at the vertices of the object grid. When rasterizing polygons, these attributes interpolate along the surface of triangles and are used to calculate the color of each of the pixels.
The simplest example (and a kind of analogue of the “hello world”) is the drawing of a triangle, at each vertex of which there is one attribute — the color:

In this case, if we assign a color to each pixel of the polygon, which is the result of linear interpolation of the colors of the three vertices, we will get the following image:
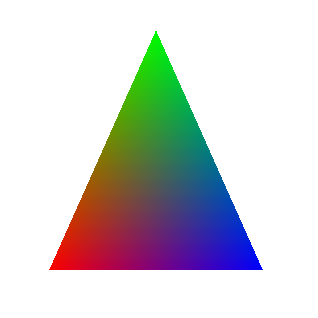
The way in which interpolation is performed depends on the data we use in the drawing process, and they, in turn, depend on the algorithm that is used in rasterization. For example, when using the "standard" algorithm, we can use simple linear interpolation of values between two pixels, and when using traversal-algorithms, barycentric coordinates. Therefore, we postpone it until the description of the algorithms themselves.
Nevertheless, there is another important topic that needs to be addressed in advance: interpolation of attributes with perspective correction.
The easiest way to interpolate is linear interpolation in screen space: after the polygon has been projected onto the projection plane, we interpolate the attributes along the surface of the triangle in a linear fashion. It is important to understand that this interpolation is not correct, since it does not take into account the projection produced.
Consider the projection of the line onto the projection plane d = 1 . At the initial and final vertices are set some attributes that vary linearly in the space of the camera (and in the world). After the projection is made, these attributes do not grow linearly in screen space. If, for example, we take the middle point in camera space ( v = v0 * 0.5 + v1 * 0.5 ), then after the projection this point will not lie in the middle of the projected line:

This is easiest to notice when texturing objects (I will use simple texturing without filtering in the examples below). I have not yet described the texturing process in detail (and this is the topic of a separate article), so for the time being I will limit myself to a brief description.
When texturing at each vertex of the polygon, the attribute value of texture coordinates is specified (it is often called uv by the name of the corresponding axes). These are the normalized coordinates (from 0 to 1 ) that determine which part of the texture will be used.
Now imagine that we want to draw a textured rectangle and set the four values of the uv attribute so that the texture is used entirely:

It seems that everything is not bad:

However, this model is parallel to the projection plane, and therefore there should be no distortion due to the perspective. Let's try to move the top two vertices by one along the z axis, and the problem will be immediately visible:

Thus, it is necessary to consider the perspective when interpolating attributes. The key fact to this is that, although z cannot be correctly interpolated in screen space, 1 / z - it can. Consider the line projection again:

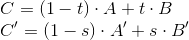
We also already know that along similar triangles:

Interpolating x in screen space, we get:

Interpolating x in camera space, we get:

These three equations are key and all subsequent formulas are derived from them. I will not give a complete conclusion, since it is easy to do this on my own, and I will describe it only briefly, focusing on the results.
Substituting these two equalities into the equation obtained from the ratios of the sides of the triangle, and simplifying all the expressions, we end up with the fact that the inverse of the z- coordinate can be linearly interpolated in screen space:
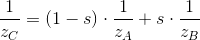
It is important that in this expression interpolation occurs between the values inverse of the z coordinates of the camera space.
Further, suppose that at the vertices A and B the values of a certain attribute are given, we denote them by T1 and T2 , which can also be linearly interpolated in the camera space:
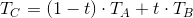
Using intermediate results from the above output, we can write down that the Tc / Zc value can also be correctly interpolated in screen space:

Summarizing, we obtained that 1 / Zc and Tc / Zc can be linearly interpolated in screen space. Now we can easily get the value of Tc :
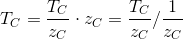
Actually, the cost of prospectively correct interpolation lies mainly in this division. If there is no great need for it, it is better to minimize the number of attributes for which it is used and to do with simple linear interpolation in screen space, if possible. Below is the correct texturing result:

To implement perspective correction, we need values that are inverse to the depth ( z- coordinate) of the vertices in the chamber space. Recall what happens when you multiply by the projection matrix:

Vertices from camera space go to clipping space. In particular, the z- coordinate is subject to certain changes (which will be needed later for the depth buffer) and no longer coincides with the z- coordinate vertex in the camera space, so we cannot use it. And what coincides is the w -coordinate, since we explicitly put z in it from the chamber space (just look at the 4th column of the matrix). In fact, we do not even need z itself, but 1 / z . And we actually get it "for free", because when we go to NDC we divide all the vertices by z (which lies in the w-coordinate):
float const w_inversed{ 1.0f / vw }; vx *= w_inversed; vy *= w_inversed; vz *= w_inversed; // NDC to screen // ... And, therefore, we can simply replace it with the opposite value:
float const w_inversed{ 1.0f / vw }; vx *= w_inversed; vy *= w_inversed; vz *= w_inversed; vw = w_inversed; // NDC to screen // ... Rasterization algorithms
Below is a description of the three approaches to the rasterization of polygons. Complete code samples will be absent, because a lot of it depends on the implementation, and this will be more confusing than help. At the end of the article there will be a link to the project, and, if necessary, you can see the implementation code in it.
"Standard" algorithm
I called this algorithm “standard” because it is the most frequently described rasterization algorithm for software renderers. It is easier to understand than traversal-algorithms and rasterization in homogeneous coordinates, and, accordingly, easier to implement.
So let's start with the triangle that we want to rasterize. Suppose, to begin with, that this is a triangle with a horizontal bottom edge.

The essence of this algorithm is to sequentially move along the side faces and paint over the pixels between them. To do this, first calculate the offset values along the X axis for each offset by one along the Y axis.

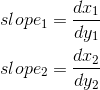
Then, the movement begins along the sides. It is important that the movement starts from the nearest center, and not from the Y- coordinates of the vertex v0 , since the pixels are represented by these points. If the Y coordinate of v0 already lies on the center, then we still move to the next center along this axis, since v0 lies on both the left and the right side, which means this pixel should not be included in the image:

When we move on to the next line, we also start the movement only from the next center along the X axis. If the face passes through the center of the pixel, then on the left side we include the pixel in the image, but not on the right one.
Similarly, the algorithm works for triangles with a horizontal upper side. Those triangles, which do not have a single horizontal side, are simply divided into two triangles - one with the horizontal top and one with the horizontal bottom. To do this, look for the intersection of the horizontal line passing through one of the vertices of the triangle (average along the Y- coordinate), with a different face:

After that, each of these triangles is rasterized according to the algorithm above. It is also necessary to correctly calculate the values of z and w coordinates in the new vertex - for example, interpolate them. Similarly, the presence of this vertex must be taken into account when interpolating attributes.
Interpolation of attributes without perspective correction occurs as follows: when moving along the side faces, we calculate the interpolated attribute values at the start and end points of the line that we are going to rasterize. Then, these values are linearly interpolated along this line. If a perspective correction is needed for an attribute, then instead we interpolate T / z along the edges of the polygon (instead of just interpolating T , the attribute value), as well as 1 / z . Then, these values at the start and end points of the line are interpolated along it and are used to get the total attribute value with perspective, according to the formula given above. It must be remembered that the 1 / z , to which I refer, actually lies in the w-coordinate of the vector after all the transformations produced.
Traversal algorithms
This is a whole group of algorithms using the same approach, based on the equations of the faces of the polygon.
The face equation is the equation of the line on which this face lies. In other words, it is an equation of a line passing through two vertices of a polygon. Accordingly, each triangle is characterized by three linear equations:

To begin with, we describe the equation of a straight line passing through two points (they are the pair of triangle vertices):

We can rewrite it as follows:
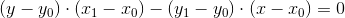

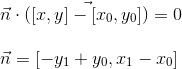
It is clear from the last expression that the vector n is perpendicular to the vector v0 - v1 (the coordinates are reversed, and the X-coordinate is taken with a minus sign). Thus, n is the normal to the line formed by two vertices. This is all the same equation of a straight line, and, therefore, substituting the point (x, y) there and getting a zero, we know that this point lies on a straight line. What about the other values? This is where the normal recording form comes in handy. We know that the scalar product of two vectors calculates the length of the projection of the first vector onto the second, multiplied by the length of the second vector. The first vector is the normal, and the second is the vector from the first vertex to the point (x, y):

And we have three possible options:
- The value is 0 - the point lies on the line
- Value greater than 0 - the point lies in the positive half-plane
- Value less than 0 - the point lies in the negative half-plane
They are all shown below:



We can also set the equation of a line so that the normal points in the opposite direction - simply multiplying it by minus one. In the following, I will assume that the equation is composed in such a way that the normal points to the inside of the triangle.
Using these equations, we can define a triangle as the intersection of three positive half-planes.
Thus, the common part of traversal-algorithms is as follows:
- Calculate the values of the equations of the faces for the point
- If all values are positive, the pixel is filled. If one of them is zero, then the pixel lies on one of the faces, and we use the top-left rule to decide whether the pixel belongs to the polygon.
- Move to the next pixel
Let us dwell on the implementation of top-left rule. Now, when we operate on the normal to the face, we can give more rigorous definitions for the left and top faces:
- The left side is the face whose normal has a positive x-coordinate (i.e. points to the right side)
- The top face is the face whose normal has a negative y-coordinate, in case the Y axis points up. If the Y axis points down (I will stick with this option), then the y-coordinate at the upper edges is positive.
It is also important to note that the coordinates of the normal coincide with the coefficients a and b in the canonical straight line equation: ax + by + c = 0 .
Below is an example of a function that determines whether a pixel is in the positive half-plane relative to one of the faces (using the top-left rule). It is enough for it to take three arguments per input: the value of the equation of a face at a point, and the coordinates of the normal:
Code example
inline bool pipeline::is_point_on_positive_halfplane_top_left( float const edge_equation_value, float const edge_equation_a, float const edge_equation_b) const { // , top-left rule // if (std::abs(edge_equation_value) < EPSILON) { if (std::abs(edge_equation_a) < EPSILON) { // edge.a == 0.0f, , , // // y- , // return edge_equation_b > 0.0f; } else { // x- , // return edge_equation_a > 0.0f; } } else { // , return edge_equation_value > 0.0f; } } Simple and useful optimization when calculating the values of equations: if we know the value in a pixel with coordinates (x, y) , then to calculate the value at the point (x + 1, y) it is enough to add the value of the coefficient a . Similarly, to calculate the value in (x, y + 1), it suffices to add the coefficient b :
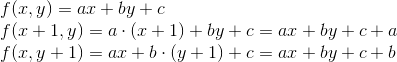
The next step is attribute interpolation and perspective correction. For this, barycentric coordinates are used. These coordinates, in which the point of the triangle is described as a linear combination of vertices (formally, implying that the point is the center of mass of the triangle, with the corresponding weight of the vertices). We will use the normalized version - i.e. the total weight of the three vertices is one:
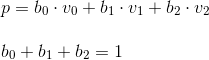

This coordinate system also has a very useful property that allows them to be calculated: the barycentric coordinates are equal to the ratio of the areas of the triangles formed in the figure above to the total area of the triangle (for this reason they are also sometimes called areal coordinates):

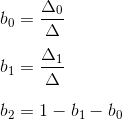
The third coordinate can be calculated not through the areas of triangles, since the sum of the three coordinates is equal to one — in fact, we have only two degrees of freedom.
Now everything is ready for linear interpolation of attributes: the attribute value at a given point of the triangle is equal to the linear combination of barycentric coordinates and attribute values at the corresponding vertices:
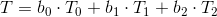
To correct the perspective, we use a different formula — first, we calculate the interpolated T / z value, then the interpolated 1 / z value, and then divide them into each other to get the final T value taking into account the perspective:
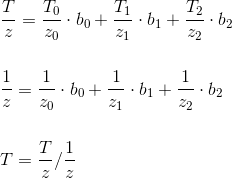
The difference between the different traversal algorithms is how the pixels are selected for verification. We will consider several options.
AABB algorithm
As the name implies, this algorithm simply builds the axis-aligned bounding box of the polygon, and traverses all the pixels inside it. Example:

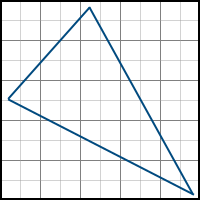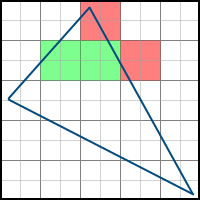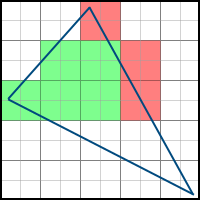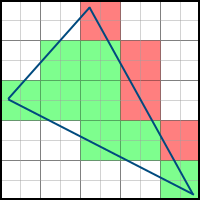
Backtracking algorithm
This algorithm consists of the following steps:
- We start with the topmost pixel below the topmost one.
- Move to the left until we meet a pixel to the left of the polygon (backtracking)
- Move to the right and paint over the pixels until we meet a pixel to the right of the polygon.
- Go to the line below and start again with the second step.
This can be represented as follows:

It is possible to check that the pixel is to the left of the polygon as follows - at least for one face, for which the normal points to the right (ie, a> 0), the value of the equation for this face is negative.
Zigzag algorithm
This algorithm can be considered as an improved version of the backtracking algorithm. Instead of “idle” passing through the pixels in the line, until there is a pixel from which we can begin to move in the right direction, we memorize information about the pixel from which we started moving on the line, and then we pass through the pixels to the left and right of him
- We start with the topmost pixel below the topmost one.
- Remember the position
- Move to the left and paint over the pixels included in the polygon, until we meet a pixel to the left of the polygon (backtracking)
- We return to the pixel from which we started (we remembered it in step 2) and move to the right, painting over the pixels entering the polygon until we meet the pixel outside the polygon
- Go to the line below and start again with the second step.

Rasterization Algorithm in Homogeneous Coordinates
This algorithm was originally described in the publication Triangle scan conversion using 2D homogeneous coordinates, Marc Olano & Trey Greer . Its main advantages are the absence of the need for clipping and dividing by the w-coordinate during the transformation of the vertices (with the exception of a couple of reservations - they will be described later).
First of all, suppose that, at the beginning of the rasterization, the x and y coordinates of the vertices contain values that are mapped to coordinates on the screen by simply dividing by the corresponding w- coordinate. This may slightly change the vertex transformation code, provided that several rasterization algorithms are supported, since it does not include division by w-coordinate. Coordinates in a homogeneous two-dimensional space are transmitted directly to the function that produces rasterization.
Let us consider in more detail the question of linear interpolation of attributes along a polygon. Since the value of the attribute (let's call it p ) grows linearly, it must satisfy the following equation (in three-dimensional space):

Since the point (x, y, z) is projected onto the plane using homogeneous coordinates (x, y, w) , where w = z , we can also write this equation in homogeneous coordinates:

Imagine that we know the coefficients a , b and c (we will consider finding them a little later). During rasterization, we deal with the coordinates of pixels in the screen space, which are related to the coordinates in a homogeneous space by the following formula (this was our initial assumption):
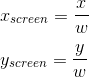
We can express the value of p / w using only coordinates in screen space, by dividing by w:

To get the correct value of p using screen coordinates, we only need to divide this value by 1 / w (or, which is the same, multiply by w ):

1 / w , in turn, can be calculated by a similar algorithm - it is enough to imagine that we have a certain parameter that is the same in all vertices: p = [1 1 1] .
Now consider how we can find the coefficients a , b and c . Since for each attribute its values are given at the vertices of the polygon, we actually have a system of equations of the form:

We can rewrite this system in matrix form:
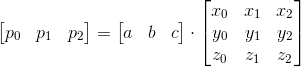
And the solution:

It is important to note that we need to count only one inverse matrix per polygon — then these coefficients can be used to find the correct attribute value at any point on the screen. Also, since we need to calculate the determinant of the matrix to invert it, we get some auxiliary information, because the determinant also calculates the volume of the tetrahedron with vertices at the origin and points of the polygon multiplied by two (this follows from the definition of the mixed product of vectors ). If the determinant is zero, this means that the polygon cannot be drawn, since it is either degenerate, or it is turned edgewise with respect to the camera. Also, the volume of a tetrahedron can be with a plus sign and a minus sign - and this can be used to cut off polygons that are turned "back" to the camera (the so-called backface culling). If we consider the order of the vertices counterclockwise to be correct, then polygons with a positive determinant value should be skipped (provided that the left-side coordinate system is used).
Thus, the question of interpolation of attributes is already resolved - we can calculate the correct value (taking into account the perspective) of any attribute at a given point on the screen. It remains only to decide which points of the screen belongs to the polygon.
Let us recall how the pixel belonging to the polygon was tested in traversal algorithms. We calculated face equations, and then checked their values at the desired point on the screen. If they were all positive (or zero, but belonged to the left or upper edges), then we painted over the pixel. Since we are already able to interpolate attributes along the surface of a triangle, we can use exactly the same approach, considering that we interpolate a certain pseudo-attribute that is zero along the face and some positive value (the most convenient is 1) at the opposite vertex (in fact, this is going through these faces):

Accordingly, the values of these pseudo-attributes for each of the faces:
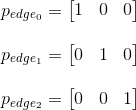
Using them we can calculate the corresponding coefficients a , b and c for each of the faces and get their equations:

Now we can interpolate their values along the surface of a triangle in a similar way and calculate their values at the point we need. If it is positive, or it is zero, but we are on the left and upper edges, the pixel is inside the polygon and must be painted over. We can also apply a small optimization - we do not need the exact values of the equations of the faces at all, its sign is enough. Therefore, dividing by 1 / w can be avoided, we can simply check the signs of p / w and 1 / w - they should be the same.
Since we operate with the same face equation, much of what is said in the section on traversal algorithms can also be applied to this algorithm. For example, top-left rule can be implemented in a similar way, and the values of face equations can be calculated incrementally, which is a useful optimization.
When presenting this algorithm, I wrote that this algorithm does not require the implementation of clipping, since it operates in homogeneous coordinates. This is almost entirely true, except for one case. There may be situations when working with w-coordinates of points that are close to the origin of the coordinates (or coincide with it). In this case, overflow may occur when interpolating attributes. So a good idea would be to add another “face”, which is located parallel to the xy plane and located at a distance of z near from the origin to avoid such errors.
When describing traversal algorithms, I mentioned several options for selecting a set of pixels that should be checked for belonging to a triangle (axis aligned bounding box, backtracking, zigzag algorithms). They can be applied here. This is a situation in which it will still be necessary to divide the vertices by the w-coordinate to calculate the boundary values (for example, the coordinates of the bounding box), we should only provide for situations where w <= 0 . Of course, there are other ways. Passing through all the pixels of the screen is obviously unsuccessful in terms of performance. You can also use tile rasterization, the description of which is beyond the scope of this article.
That's all
A project where you can see examples of implementations: github.com/loreglean/lantern . Pull requests with fixes and other things are welcome, it is better to write about errors in the code or questions about it in PM.
Source: https://habr.com/ru/post/257107/
All Articles