Linear algebra: test run
Hi, Habr!
Analit, ruler, linal - these words are associated more with the phrase “pass and forget”, and not with the fact that we really need a wonderful branch of mathematics called linear algebra. Let's try to look at it from different sides and see what is good in it and why it is so useful in applications.
Often, the first acquaintance with linear algebra looks like this:
')

Not very inspiring, right? Two questions immediately arise: where did all this come from and why is it needed.
When I was working on computational fluid dynamics (CFD), one of my colleagues said: “We do not solve the Navier-Stokes equations. We reverse matrices. ”Indeed, linear algebra is the“ workhorse ”of computational mathematics:

I will try to illustrate this connection in a simpler example than hydrodynamics.
Suppose we have a thin metal rod with fixed ends, the temperature of which is maintained equal to zero. We begin to heat the rod using a distributed heat source, which emits q (x) Joules per second per unit length of the rod in the vicinity of point x . What temperature t = t (x) will be established? Let's make a very rough sketch of the model. When equilibrium is established, for each segment [xh, x + h] of our rod the heat influx from the source should be equal to the sum of the heat fluxes across the segment boundaries. If h is sufficiently small, then, up to constants (which will include h , yes readers will forgive me), this equality can be written as:

where Q xh is the heat flux through the left boundary, and Q x + h through the right one. According to Fourier's law, the heat flux is proportional to the temperature difference (after all, if you dive into the pool, then in the first seconds it will be the coldest). Therefore (up to constants containing h )

Let h = 1 / N. Consider points of the form x i = i · h , where i = 0, 1, 2, ..., N. They are called mesh. Then the variables t i = t (x i ) will satisfy the equations

where we have already taken into account the boundary conditions, and q i = q (x i ) . Well, we got a system of linear equations:

Specifically, this system can be solved "in the forehead" by the so-called sweep method, but in real models the systems become more complicated. This is where linear algebra comes to the rescue, which allows
And this is only a look at linear algebra from the point of view of mathematical modeling. And then there is quantum mechanics, statistics, and more.
As another example, I will cite the well-known problem of link ranking the pages of one site (or the Internet as a whole).
There are N pages, each of which may contain links to other pages. It is required to determine which pages are the most important. How to measure “importance” is part of the task. We will represent it quantitatively as a non-negative number (weight). Let's start with a natural assumption: the more links to this page, the greater its weight. This approach has the following disadvantage: we do not take into account the weight of the referring pages. It is logical that a link from a page that has more weight should be of greater importance. These arguments lead us to this model:

where a ij is the number of links to the i- th page from the j- th, divided by the total number of links from the j- th page. This formula can be read as follows: the weight of the i- th page is equal to the sum of the products of the weight of the j -th page to the fraction of links from the j -th page to the i -th. Thus, we have reduced our problem to a system of linear equations. Moreover, the weight vector p turns out to be an eigenvector of the matrix A , corresponding to the eigenvalue 1:

The existence of this vector (strictly speaking, for a slightly modified matrix A ) is guaranteed by the Frobenius-Perron theorem. And you can find it by simple iterations.
So, linear algebra is a very versatile set of ideas and tools that can be applied in many different areas. But only cheese in a mousetrap is free, and one has to pay for universality: some definitions and theorems may seem overly abstract and confusing. But this is not so: in fact, many abstractions are designed to simplify life, and not complicate it. “If it looks like a duck, swims like a duck and quacks like a duck, then it’s probably a duck” is essentially an abstraction, and very convenient if you get used to it. The same with linear algebra. To illustrate this point a little more specifically, let's supplement our “visual inspection” with a brief discussion of what is inside.
Linear algebra studies vector spaces and functions that map one vector space to another. We mainly consider linear functions (satisfying the relation f (α · x + β · y) = α · f (x) + β · f (y) for any numbers α and β and any vectors x and y ). There are also non-linear (for example, quadratic forms). But first of all, you need to understand what a vector is (and vector space). And this is not as trivial as it might seem.
Textbooks and courses usually provide an abstract definition of 8 points. It is also sometimes said that the vector space is an additively written Abelian group in which multiplication by scalars is defined, satisfying 4 axioms. But for those who study linear algebra for the first time, this is unlikely to help to understand. It is much easier to consider a few specific examples, and see an analogy in them. And the definition of 8 points is just a formalization of this analogy. Therefore, we proceed immediately to the examples.
Directed segments familiar to everyone from school are of course vectors. The set of directed segments is an example of a vector space. Now consider polynomials. They can be added to each other and multiplied by numbers. Note: from the point of view of algebra, these operations of adding polynomials and multiplying a polynomial by a number work exactly according to the same rules as for directed segments. For example, the equality x + y = y + x (commutativity) holds for both directed segments and polynomials. Therefore, the set of polynomials is a vector space, and the polynomials are vectors.
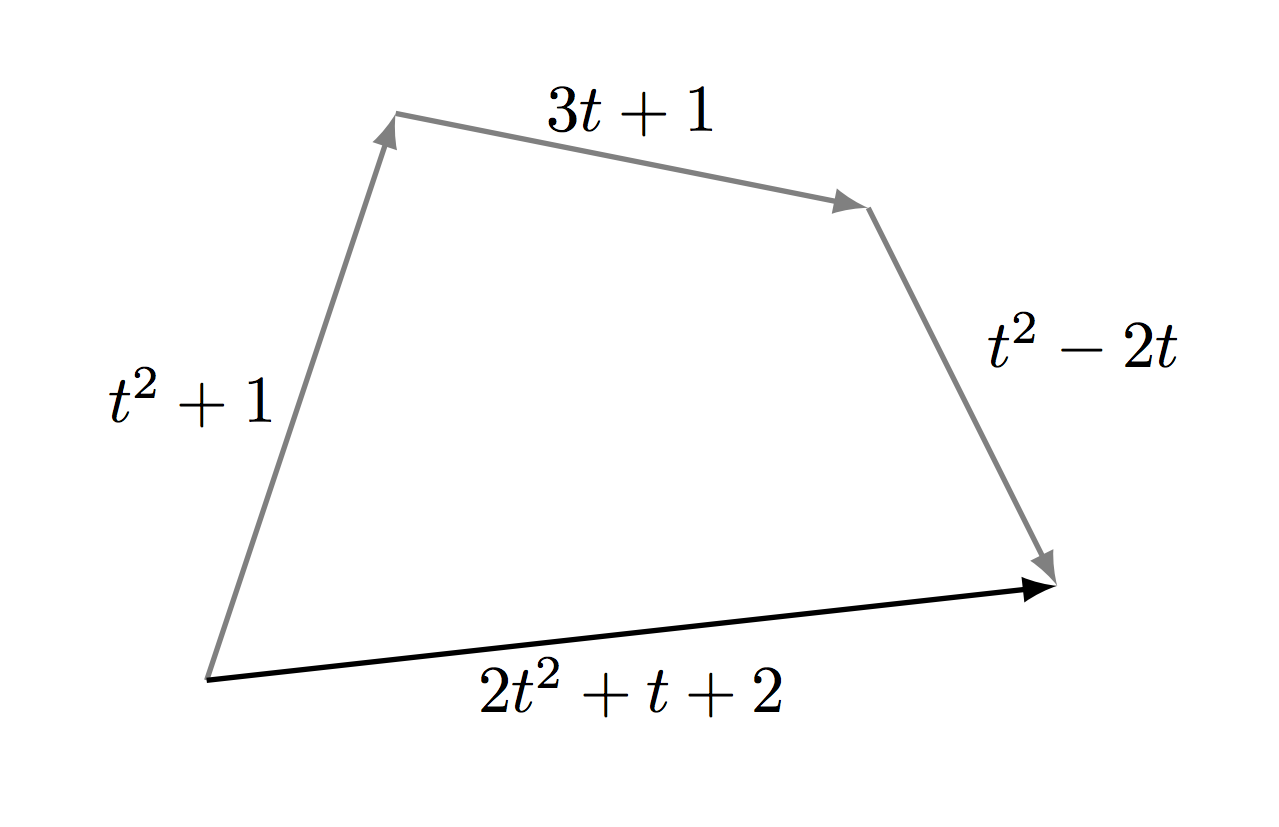
Since polynomials are similar to directed segments, then they must also have coordinates. But how to find them and how many coordinates of a polynomial? It is well known that on a plane each vector has exactly two coordinates, and in space - three. Why is this so? And what is the dimension in general? Linear algebra gives the answer to this question: dimension is the maximum number of linearly independent vectors. What does linearly independent mean? Vectors x 1 , x 2 , ..., x n are called linearly dependent if there are numbers α 1 , α 2 , ..., α n , at least one of which is non-zero, such that

If the vectors are not linearly dependent, then they are called linearly independent. (The concept of linear dependence generalizes the concepts of parallel and complanar vectors: two vectors are linearly dependent if and only if they are parallel. Three vectors are linearly dependent if and only if they are coplanar.)
The dimension of space can be either finite (the space of polynomials of degree not higher than N ) or infinite (the space of all polynomials). Both cases are encountered in practice, but let's confine ourselves to finite-dimensional ones. Let the vectors x 1 , x 2 , ..., x n be linearly independent and n be the dimension of the space. Then any other vector x can be written as a linear combination of x 1 , x 2 , ..., x n , and uniquely. The coefficients of the corresponding linear combination are called coordinates.
Now we have a strict definition of coordinates. But this is not only the point: along the way we are confronted with more fundamental (and less noticeable) concepts of linear combination and linear dependence. And we also learned that there can be no more than n linearly independent vectors in an n- dimensional linear space. This fact is one of the cornerstones of linear algebra.
It would seem that we still know too little to extract at least some benefit from it. However, now we can solve problems that at first glance are not related to linear algebra. For example, such: given the polynomials p and q ; Is there a polynomial in two variables R = R (x, y) such that R (p (t), q (t)) = 0 for all t ?
Meanwhile, our "test drive" is coming to an end. But it remains to briefly discuss the various ways of studying linear algebra. I will confine here a small overview of my own experience and try to give a couple of tips based on it.
My acquaintance with linear algebra began with the independent study of the book by OV Manturova and N.M. Matveyev "Course of higher mathematics" when I was in school. This book is not the best (but not the worst) source of knowledge in this area. It just became the first textbook on higher mathematics that fell into my hands, and its content seemed more interesting than the school curriculum. Although now we can say with certainty: there are a lot of other books that students should (and it will be no less interesting) to study first. For example, “How to solve non-standard problems” (A.Ya. Kanel-Belov, A.K. Kovaldzhi) or “Leningrad mathematical circles” (S.A. Gen., Itenberg I.V., Fomin D.V.). If you take to study linear algebra from books, then you should be patient: it may take longer to achieve the desired result than it seems.
I still owe my basic knowledge of linear algebra (and many other branches of mathematics) to L.I. Kovalenko - the legendary teacher of MIPT, whose seminars and consultations were always collected sold out. It is difficult to overestimate the attention that she provided to each student, accepting tasks and so-called “cards” - individual tasks until late at night. And during these deals, we actively communicated with each other. All this allowed not only to quickly master what is written in the textbooks, but also what is not there - intuition, cunning devices and so on.
Live communication of students with teachers (and with each other) is no substitute, and this is an advantage of traditional courses. But when I myself worked as an assistant and conducted seminars, there was often a desire to automate some things, so that there was more time for meaningful communication. Does a student need to wait for a meeting with a teacher to get a standard answer to a standard question? Or to find out if such a standard problem has been solved correctly? However, students should not be underestimated: for the most part, they themselves feel good when they do “almost meaningless work”, and this also demotivates them. Testing a proof or a solution method is one thing, but, let's say, checking a solution to a system of linear equations you can almost completely trust a computer. Moreover, in many cases, it is possible to automate not only checking the answer, but also part of the solution itself - for example, elementary matrix transformations .
So,
Analit, ruler, linal - these words are associated more with the phrase “pass and forget”, and not with the fact that we really need a wonderful branch of mathematics called linear algebra. Let's try to look at it from different sides and see what is good in it and why it is so useful in applications.
Often, the first acquaintance with linear algebra looks like this:
')

Not very inspiring, right? Two questions immediately arise: where did all this come from and why is it needed.
Let's start with practice
When I was working on computational fluid dynamics (CFD), one of my colleagues said: “We do not solve the Navier-Stokes equations. We reverse matrices. ”Indeed, linear algebra is the“ workhorse ”of computational mathematics:

I will try to illustrate this connection in a simpler example than hydrodynamics.
Suppose we have a thin metal rod with fixed ends, the temperature of which is maintained equal to zero. We begin to heat the rod using a distributed heat source, which emits q (x) Joules per second per unit length of the rod in the vicinity of point x . What temperature t = t (x) will be established? Let's make a very rough sketch of the model. When equilibrium is established, for each segment [xh, x + h] of our rod the heat influx from the source should be equal to the sum of the heat fluxes across the segment boundaries. If h is sufficiently small, then, up to constants (which will include h , yes readers will forgive me), this equality can be written as:

where Q xh is the heat flux through the left boundary, and Q x + h through the right one. According to Fourier's law, the heat flux is proportional to the temperature difference (after all, if you dive into the pool, then in the first seconds it will be the coldest). Therefore (up to constants containing h )

Let h = 1 / N. Consider points of the form x i = i · h , where i = 0, 1, 2, ..., N. They are called mesh. Then the variables t i = t (x i ) will satisfy the equations

where we have already taken into account the boundary conditions, and q i = q (x i ) . Well, we got a system of linear equations:

Specifically, this system can be solved "in the forehead" by the so-called sweep method, but in real models the systems become more complicated. This is where linear algebra comes to the rescue, which allows
- write the system in short form A · y = b (this is where the multiplication of matrices came from!);
- see if it has a solution and whether it is the only one;
- (in this example) find it using the simple formula y = A -1 b , as if A is a number;
- (flowing into computational mathematics) to construct effective numerical methods for solving systems of linear equations.
And this is only a look at linear algebra from the point of view of mathematical modeling. And then there is quantum mechanics, statistics, and more.
As another example, I will cite the well-known problem of link ranking the pages of one site (or the Internet as a whole).
There are N pages, each of which may contain links to other pages. It is required to determine which pages are the most important. How to measure “importance” is part of the task. We will represent it quantitatively as a non-negative number (weight). Let's start with a natural assumption: the more links to this page, the greater its weight. This approach has the following disadvantage: we do not take into account the weight of the referring pages. It is logical that a link from a page that has more weight should be of greater importance. These arguments lead us to this model:

where a ij is the number of links to the i- th page from the j- th, divided by the total number of links from the j- th page. This formula can be read as follows: the weight of the i- th page is equal to the sum of the products of the weight of the j -th page to the fraction of links from the j -th page to the i -th. Thus, we have reduced our problem to a system of linear equations. Moreover, the weight vector p turns out to be an eigenvector of the matrix A , corresponding to the eigenvalue 1:

The existence of this vector (strictly speaking, for a slightly modified matrix A ) is guaranteed by the Frobenius-Perron theorem. And you can find it by simple iterations.
So, linear algebra is a very versatile set of ideas and tools that can be applied in many different areas. But only cheese in a mousetrap is free, and one has to pay for universality: some definitions and theorems may seem overly abstract and confusing. But this is not so: in fact, many abstractions are designed to simplify life, and not complicate it. “If it looks like a duck, swims like a duck and quacks like a duck, then it’s probably a duck” is essentially an abstraction, and very convenient if you get used to it. The same with linear algebra. To illustrate this point a little more specifically, let's supplement our “visual inspection” with a brief discussion of what is inside.
Now a little theory
Linear algebra studies vector spaces and functions that map one vector space to another. We mainly consider linear functions (satisfying the relation f (α · x + β · y) = α · f (x) + β · f (y) for any numbers α and β and any vectors x and y ). There are also non-linear (for example, quadratic forms). But first of all, you need to understand what a vector is (and vector space). And this is not as trivial as it might seem.
Textbooks and courses usually provide an abstract definition of 8 points. It is also sometimes said that the vector space is an additively written Abelian group in which multiplication by scalars is defined, satisfying 4 axioms. But for those who study linear algebra for the first time, this is unlikely to help to understand. It is much easier to consider a few specific examples, and see an analogy in them. And the definition of 8 points is just a formalization of this analogy. Therefore, we proceed immediately to the examples.
Directed segments familiar to everyone from school are of course vectors. The set of directed segments is an example of a vector space. Now consider polynomials. They can be added to each other and multiplied by numbers. Note: from the point of view of algebra, these operations of adding polynomials and multiplying a polynomial by a number work exactly according to the same rules as for directed segments. For example, the equality x + y = y + x (commutativity) holds for both directed segments and polynomials. Therefore, the set of polynomials is a vector space, and the polynomials are vectors.

Since polynomials are similar to directed segments, then they must also have coordinates. But how to find them and how many coordinates of a polynomial? It is well known that on a plane each vector has exactly two coordinates, and in space - three. Why is this so? And what is the dimension in general? Linear algebra gives the answer to this question: dimension is the maximum number of linearly independent vectors. What does linearly independent mean? Vectors x 1 , x 2 , ..., x n are called linearly dependent if there are numbers α 1 , α 2 , ..., α n , at least one of which is non-zero, such that

If the vectors are not linearly dependent, then they are called linearly independent. (The concept of linear dependence generalizes the concepts of parallel and complanar vectors: two vectors are linearly dependent if and only if they are parallel. Three vectors are linearly dependent if and only if they are coplanar.)
The dimension of space can be either finite (the space of polynomials of degree not higher than N ) or infinite (the space of all polynomials). Both cases are encountered in practice, but let's confine ourselves to finite-dimensional ones. Let the vectors x 1 , x 2 , ..., x n be linearly independent and n be the dimension of the space. Then any other vector x can be written as a linear combination of x 1 , x 2 , ..., x n , and uniquely. The coefficients of the corresponding linear combination are called coordinates.
Now we have a strict definition of coordinates. But this is not only the point: along the way we are confronted with more fundamental (and less noticeable) concepts of linear combination and linear dependence. And we also learned that there can be no more than n linearly independent vectors in an n- dimensional linear space. This fact is one of the cornerstones of linear algebra.
It would seem that we still know too little to extract at least some benefit from it. However, now we can solve problems that at first glance are not related to linear algebra. For example, such: given the polynomials p and q ; Is there a polynomial in two variables R = R (x, y) such that R (p (t), q (t)) = 0 for all t ?
Meanwhile, our "test drive" is coming to an end. But it remains to briefly discuss the various ways of studying linear algebra. I will confine here a small overview of my own experience and try to give a couple of tips based on it.
Wikipedia Book - the best source of knowledge
My acquaintance with linear algebra began with the independent study of the book by OV Manturova and N.M. Matveyev "Course of higher mathematics" when I was in school. This book is not the best (but not the worst) source of knowledge in this area. It just became the first textbook on higher mathematics that fell into my hands, and its content seemed more interesting than the school curriculum. Although now we can say with certainty: there are a lot of other books that students should (and it will be no less interesting) to study first. For example, “How to solve non-standard problems” (A.Ya. Kanel-Belov, A.K. Kovaldzhi) or “Leningrad mathematical circles” (S.A. Gen., Itenberg I.V., Fomin D.V.). If you take to study linear algebra from books, then you should be patient: it may take longer to achieve the desired result than it seems.
I still owe my basic knowledge of linear algebra (and many other branches of mathematics) to L.I. Kovalenko - the legendary teacher of MIPT, whose seminars and consultations were always collected sold out. It is difficult to overestimate the attention that she provided to each student, accepting tasks and so-called “cards” - individual tasks until late at night. And during these deals, we actively communicated with each other. All this allowed not only to quickly master what is written in the textbooks, but also what is not there - intuition, cunning devices and so on.
Live communication of students with teachers (and with each other) is no substitute, and this is an advantage of traditional courses. But when I myself worked as an assistant and conducted seminars, there was often a desire to automate some things, so that there was more time for meaningful communication. Does a student need to wait for a meeting with a teacher to get a standard answer to a standard question? Or to find out if such a standard problem has been solved correctly? However, students should not be underestimated: for the most part, they themselves feel good when they do “almost meaningless work”, and this also demotivates them. Testing a proof or a solution method is one thing, but, let's say, checking a solution to a system of linear equations you can almost completely trust a computer. Moreover, in many cases, it is possible to automate not only checking the answer, but also part of the solution itself - for example, elementary matrix transformations .
So,
- ideas and methods of linear algebra are easiest to understand when solving interesting problems (including those from other areas: this will allow a better understanding of abstract concepts);
- the best thing to do is not alone, but with friends and a good teacher (various forums are still very useful);
- if you are demotivated by routine actions - use online courses and other ways of automation (here you need to have a sense of proportion. For example, before turning the matrix into Wolfram Alpha, you should learn how to do it with a pen and paper);
- books allow you to move in, but do not forget to keep track of time;
- the basic concepts and theorems of linear algebra did not appear from scratch. It is useful to seek to understand the motivation, internal logic and develop their intuitive vision of the subject. After all, it was probably interesting for Cramer, Gauss, Peano and many others to discover (first of all for themselves) these basics; Why should those who study linear algebra now be bored?
Source: https://habr.com/ru/post/256275/
All Articles