Wolfram Language (Mathematica) in Russian ... or advanced function assignment

Download the post in the form of a Mathematica document, which contains all the code used, here .

One of the most important skills in working with the Mathematica system is the assignment of functions that would have the most different forms, and would depend on a different number of variables (from literally no variable to an infinite number of variables), while some variables could have values which are used by default if their specific values ​​are not entered, others would have the appearance of options, like many functions built into Mathematica , or would have strict restrictions on their type ...

This post will show you how to program in Mathematica in Russian, and for this I will show you how to create functions whose names are given in Cyrillic, corresponding to the original built-in functions. In this case, you will learn how to actually set the most different types and types of functions.
')
I would like to note that in version 10.1 of the Wolfram Language ( Mathematica ), the process of Russification of the interface, documentation and predictive interface began. For a number of languages, for example, Chinese, the process of full localization is almost complete. Moreover, even Wolfram | Alpha will soon be able to work in Chinese.

Creating standard functions of several variables

Deferred function setting

You can set a standard function using the following structure:



This construction involves three extremely important Mathematica functions, the first is the delayed assignment SetDelayed (in short form it looks like = ), the second is the template expression Blank [] (in short form it looks like _ ), the third is the template with the name Pattern assigned to it [name, object] (in short form has the form name: object , or, if the template object is simply _ , then name_ ).

Let us consider in more detail why they are needed and how they work.

• Deferred assignment : = used in the form:

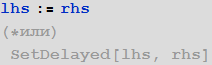
it assigns the expression rhs (short for “right hand side” to the right) as a delayed value of the object (symbol) lhs (short for left hand to hand is left), while the expression rhs remains in an uncalculated form. As soon as the lhs object is found in the code, it is replaced with the rhs expression, which is then evaluated.

• The template expression _ is used in the form:

or



it represents any expression written in the Wolfram Language. In this case, the _h pattern specifies any expression whose head part matches h .

• The template with the name_ assigned to it is used in the form:

or



it serves to “transfer” the object inside the functional structures used (replacement rules, setting functions, etc.)

Well, summing up the above, we can say that the standard definition of the function of one variable is:



which in its full form (in the one that actually “sees” it and uses Mathematica ) looks like this:



Setting a function in the form of a deferred assignment, which in general has the form:

f [pattern]: = lhs

works as follows:

• As soon as Mathematica encounters a function called f in the code, it compares its calculated argument expr (if it meets the expression f [expr] ) with the pattern pattern . In the event that the expression expression expr satisfies the pattern pattern , then the f [expr] construct is replaced with the lhs expression, in which all characters with the name corresponding to the pattern expression name pattern are replaced with the expr expression, after which the resulting construct is evaluated and replaces the original expression f [expr] .

It is clear that if you use a function of the form f [v _]: = lhs [v] , then, as mentioned above, any expression expr will satisfy the pattern v_ .

I will give an example. Define a function that calculates :



Let's try to calculate its value from different arguments:









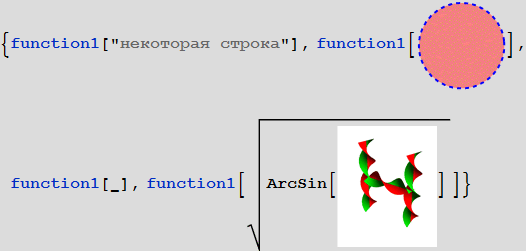
As can be seen from the examples discussed above, indeed any object (number, symbol, picture) satisfies the x_ pattern and Mathematica works easily with all expressions, which demonstrates the extraordinary flexibility of its language.

Setting the function of many variables is completely analogous. Let's say we give the function 3 variables:

Creating a function that “remembers” its previously calculated values

If you change the deferred function setting as follows:



then once having calculated the value at some “point” (the value for a certain value of the argument, the argument may not be a number and not necessarily a point in its usual sense ...), the function f will remember (though only for this Mathematica session) this value ( here the Set function was used (in short form it looks like = ), which allows assigning some value to some symbol).

Such a function assignment can save a lot of time, if the calculation of the right side of the delayed assignment of a function takes a lot of time, but it requires more memory.

An example (the time to calculate a certain command can be found using the Timing function):











From the example it can be seen that once having calculated the value of a function at a point, with this setting of the function, next time it will not take any time.

• Attention! Such an assignment can play a cruel joke with you. Since the value of the function at this point is stored in memory, it becomes insensitive to changes in the right-hand side of the lhs [v] function:

Absolute function assignment

If, instead of using the SetDelayed ( : = ) function, you use the Set ( = ) function in the function definition:



then the right expression lhs [v] will be calculated immediately, after which the values ​​of the function arguments will be substituted into it when a further expression of the form f [expr] is encountered in the code. This form of setting a function can save time if the evaluation of the expression lhs [v] is laborious and, in fact, does not depend on the specific value of the argument v .

Compare the deferred and absolute assignments of functions.

The calculation of the lhs [v] expression does not depend on the value of v directly:















The calculation of the lhs [v] expression depends on the value of v directly:















From the two examples above, two important conclusions can be drawn:

• Attention! The absolute task can be used only if the calculation of the lhs [v] construct does not directly depend on the variable v . If this is not the case, the answer may not be correct.

• In the case of the absolute assignment of functions, you get the opportunity to significantly speed up your calculations in a situation where the computation of the right side of the assignment of a function does not directly depend on the argument.

Setting a function, some arguments of which have default values

In some situations it is convenient to use functions, some variables of which would have default values. You can set a variable of this kind for a function using the Optional function, which is used as follows:



Let us set a function that builds a circle or a circle, while by default the center of this circle (circle) is at the point (0, 0), it (she) has a radius of 1, and also has a red color:























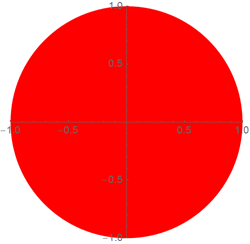
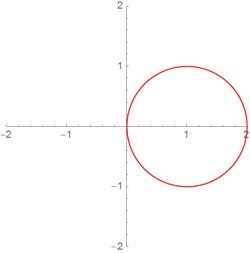
The obvious inconvenience of working with such functions is that if you want to use a lot of arguments with default values, you can only use these values ​​if they are to the right of those arguments to which you attach some value. If you change some default value to a specific value, then you will have to explicitly specify all the values ​​that are to the left of it. Thus, this task is very sensitive to the order of the arguments, which means that variables with default values ​​should be placed in order of decreasing frequency of their use, if the frequency is about the same, then the expediency of setting such functions drops sharply.

Setting a function with options

In order to get rid of the problem associated with the use of variables that have default values, which was discussed above, functions that have so-called options are used. Most of the built-in functions of Mathematica have certain options.

To set options for a certain function, use the built-in functions OptionsPattern and OptionValue , the meaning of which is clear from the following example: we implement the same function as before (building a circle or circle with the default center at (0, 0) ), radius 1, red color), only all default values ​​are now defined by options:

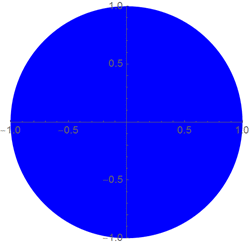
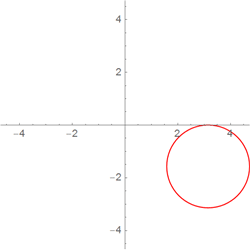
Setting a function with conditions imposed on arguments

In order to impose a constraint on a function argument, the Condition function (which has a short form /; ) is used.

Let's say we create a function that would be calculated only if its argument is greater than 2:







Or a function that would be calculated if its argument is a list consisting of no more than 4 elements:







In the example above, a template was also used with the head of the expression List ( x_List ), which specifies any list.

This kind of patterns can be very different:







You can also use all sorts of test functions that check whether an expression has a certain property. This is done using the PatternTest function (which has a short form ? ), The standard syntax of which is as follows:



All tests (as can be seen from the code below, there are 128 of them) in Mathematica are functions that end up, as a rule, with a capital Q :






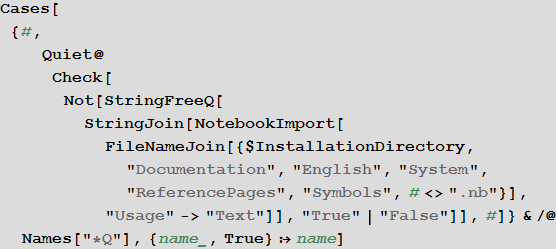
128

Let's say it’s just so easy to create a function that will work only with prime numbers:

Alternative templates

In some cases, the function must work with an expression if it satisfies one of the specified patterns. You can implement a similar construct using the Alternatives function (which has a short form | ).

Below is a function whose argument can be either a list or an integer greater than 4:

Multiple function assignment (function overload)

In Mathematica , you have the opportunity to define the function definitions that will be used in different situations. This can be done by applying patterns with the head parts of expressions, as well as using constraints imposed on variables.

In the example below, a function is created that processes input data in different ways depending on their type:

Example: composition of previously described methods for defining functions and its arguments

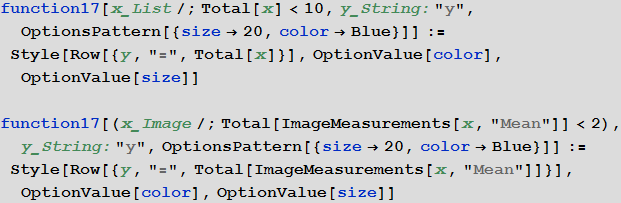
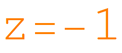
Programming in Mathematica in Russian

Now that we know how functions are defined, we can set ourselves the following task: to make it possible to program in Mathematica in Russian in compliance with the main paradigms: the built-in functions are capitalized and their names correspond exactly to the action they perform .

For this, you need to make Russian analogues of built-in functions.

Let's start with the Plot function, in Russian it will correspond to the Graph function. The syntax of the Plot function is:



Her Russian equivalent will be completely analogous.

To begin with, we will find out the list of all the options of the Plot function and their default values, this can be done using the Options function:





Now we will create this list in Russian (some options are omitted here, which, by experience, are used extremely rarely when plotting):



Now let's set the connection of Russian names with embedded analogs:



Now we can set the Russian equivalent of the Plot function:



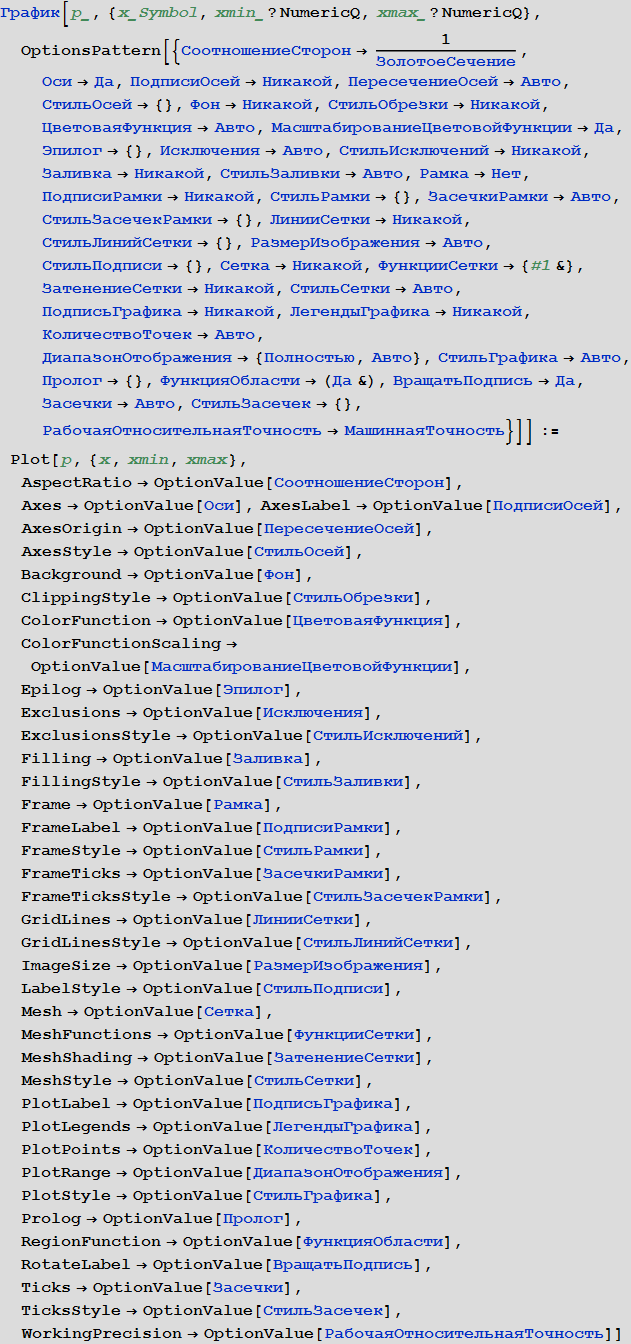
We also need some standard notation for the thickness and color of the lines:



Similarly, we define the Solve function — the Russian analogue of the Solve function; Absolute Point Size — AbsolutePointSize ; Point — Point ; Line — Line :



Let's try to create some schedule:









Thus, in Mathematica it is possible to create a package that will allow programming in ordinary Russian, just as it was done in the USSR, say in the ALMIR-65 language.

If any of you have a desire to develop this idea, then it is quite possible to make Mathematica work in Russian.