Algorithms for fast calculation of factorial
The concept of factorial is known to all. This is a function that calculates the product of consecutive positive integers from 1 to N inclusive: N! = 1 * 2 * 3 * ... * N. Factorial is a fast-growing function, already for small values of N the value of N! has a lot of meaningful numbers.
Let's try to implement this function in a programming language. Obviously, we need a language that supports long arithmetic. I will use C #, but you might as well take Java or Python.
Naive algorithm
')
So, the simplest implementation (let's call it naive) is obtained directly from the definition of factorial:
On my machine, this implementation runs for about 1.6 seconds for N = 50,000.
Next, we consider algorithms that work much faster than a naive implementation.
Tree calculation algorithm
The first algorithm is based on the consideration that long numbers of approximately the same length are more efficient to multiply than a long number to multiply by a short one (as in the naive implementation). That is, we need to ensure that, when calculating factorial, the factors are always approximately the same length.
Suppose we need to find the product of consecutive numbers from L to R, denote it as P (L, R). Divide the interval from L to R in half and count P (L, R) as P (L, M) * P (M + 1, R), where M is midway between L and R, M = (L + R) / 2 Note that the multipliers will be about the same length. Similarly, we divide P (L, M) and P (M + 1, R). We will perform this operation until no more than two factors remain in each interval. It is obvious that P (L, R) = L, if L and R are equal, and P (L, R) = L * R, if L and R differ by one. To find N! you need to calculate P (2, N).
Let's see how our algorithm will work for N = 10, find P (2, 10):
P (2, 10)
P (2, 6) * P (7, 10)
(P (2, 4) * P (5, 6)) * (P (7, 8) * P (9, 10))
((P (2, 3) * P (4)) * P (5, 6)) * (P (7, 8) * P (9, 10))
(((2 * 3) * (4)) * (5 * 6)) * ((7 * 8) * (9 * 10))
((6 * 4) * 30) * (56 * 90)
(24 * 30) * (5,040)
720 * 5,040
3,628,800
It turns out a kind of tree, where the factors are located in the nodes, and the result is obtained in the root

We implement the described algorithm:
For N = 50,000, factorial is calculated in 0.9 seconds, which is almost twice as fast as in a naive implementation.
Algorithm for calculating factorization
The second fast calculation algorithm uses factorial factorization (factorization). Obviously, in the decomposition of N! only simple factors from 2 to N are involved. Let us try to calculate how many times the simple factor K is contained in N !, that is, we find out the degree of the factor K in the decomposition. Each K-th member of the product 1 * 2 * 3 * ... * N increases the index by one, that is, the exponent will be equal to N / K. But each K 2 -th term increases the degree by one more, that is, the indicator becomes N / K + N / K 2 . Similarly for K 3 , K 4 and so on. As a result, we obtain that the exponent with a simple multiplier K will be N / K + N / K 2 + N / K 3 + N / K 4 + ...
For clarity, we calculate how many times a deuce is in 10! Every second gives a factor of two (2, 4, 6, 8 and 10), a total of 10/2 = 5 of such factors. Every fourth gives a four (2 2 ), a total of 10/4 = 2 (4 and 8). Every eighth gives an eight (2 3 ), such a factor is only one 10/8 = 1 (8). Sixteen (2 4 ) and more are not given by any factor, which means that the calculation can be completed. Summing up, we get that the exponent with two in the decomposition of 10! for prime factors will be 10/2 + 10/4 + 10/8 = 5 + 2 + 1 = 8.
If you act in the same way, you can find the indicators at 3, 5 and 7 in the decomposition of 10!, After which it remains only to calculate the value of the product:
ten! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
It remains to find the prime numbers from 2 to N, for this you can use the sieve of Eratosthenes :
This implementation also takes about 0.9 seconds to compute 50,000!
GMP Library
As pomme rightly noted, the factorial calculation speed is 98% dependent on the speed of multiplication. Let's try to test our algorithms by implementing them in C ++ using the GMP library. The test results are given below, it turns out that the multiplication algorithm in C # has a rather strange asymptotics, so the optimization gives a relatively small gain in C # and a huge one in C ++ with GMP. However, this issue is probably worth a separate article.
Performance comparison
All algorithms were tested for N equal to 1,000, 2,000, 5,000, 10,000, 20,000, 50,000, and 100,000 with ten iterations. The table shows the average time in milliseconds.
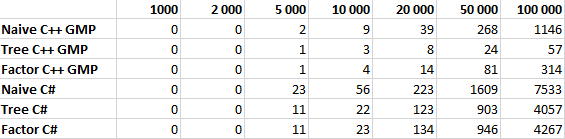
Linear graph
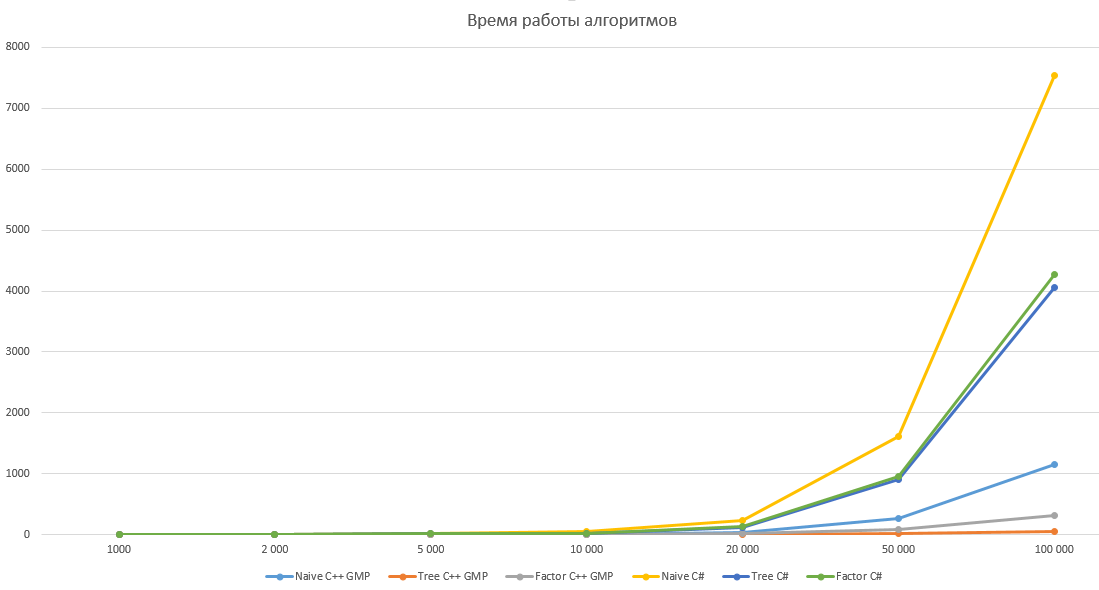
Graph with logarithmic scale
Ideas and algorithms from comments
Habrazhiteli offered a lot of interesting ideas and algorithms in response to my article, here I will leave links to the best of them
lany parallelized the tree in Java using the Stream API and received acceleration 18 times
Mrrl proposed factoring optimization by 15-20%
PsyHaSTe proposed improving naive implementation
Krypt offered a parallelized version on C #
SemenovVV proposed implementation on Go
pomme suggested using GMP
ShashkovS proposed a fast Python algorithm.
Source codes
The source codes of the implemented algorithms are listed under the spoilers.
Let's try to implement this function in a programming language. Obviously, we need a language that supports long arithmetic. I will use C #, but you might as well take Java or Python.
Naive algorithm
')
So, the simplest implementation (let's call it naive) is obtained directly from the definition of factorial:
static BigInteger FactNaive(int n) { BigInteger r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } On my machine, this implementation runs for about 1.6 seconds for N = 50,000.
Next, we consider algorithms that work much faster than a naive implementation.
Tree calculation algorithm
The first algorithm is based on the consideration that long numbers of approximately the same length are more efficient to multiply than a long number to multiply by a short one (as in the naive implementation). That is, we need to ensure that, when calculating factorial, the factors are always approximately the same length.
Suppose we need to find the product of consecutive numbers from L to R, denote it as P (L, R). Divide the interval from L to R in half and count P (L, R) as P (L, M) * P (M + 1, R), where M is midway between L and R, M = (L + R) / 2 Note that the multipliers will be about the same length. Similarly, we divide P (L, M) and P (M + 1, R). We will perform this operation until no more than two factors remain in each interval. It is obvious that P (L, R) = L, if L and R are equal, and P (L, R) = L * R, if L and R differ by one. To find N! you need to calculate P (2, N).
Let's see how our algorithm will work for N = 10, find P (2, 10):
P (2, 10)
P (2, 6) * P (7, 10)
(P (2, 4) * P (5, 6)) * (P (7, 8) * P (9, 10))
((P (2, 3) * P (4)) * P (5, 6)) * (P (7, 8) * P (9, 10))
(((2 * 3) * (4)) * (5 * 6)) * ((7 * 8) * (9 * 10))
((6 * 4) * 30) * (56 * 90)
(24 * 30) * (5,040)
720 * 5,040
3,628,800
It turns out a kind of tree, where the factors are located in the nodes, and the result is obtained in the root

We implement the described algorithm:
static BigInteger ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r - l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } static BigInteger FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } For N = 50,000, factorial is calculated in 0.9 seconds, which is almost twice as fast as in a naive implementation.
Algorithm for calculating factorization
The second fast calculation algorithm uses factorial factorization (factorization). Obviously, in the decomposition of N! only simple factors from 2 to N are involved. Let us try to calculate how many times the simple factor K is contained in N !, that is, we find out the degree of the factor K in the decomposition. Each K-th member of the product 1 * 2 * 3 * ... * N increases the index by one, that is, the exponent will be equal to N / K. But each K 2 -th term increases the degree by one more, that is, the indicator becomes N / K + N / K 2 . Similarly for K 3 , K 4 and so on. As a result, we obtain that the exponent with a simple multiplier K will be N / K + N / K 2 + N / K 3 + N / K 4 + ...
For clarity, we calculate how many times a deuce is in 10! Every second gives a factor of two (2, 4, 6, 8 and 10), a total of 10/2 = 5 of such factors. Every fourth gives a four (2 2 ), a total of 10/4 = 2 (4 and 8). Every eighth gives an eight (2 3 ), such a factor is only one 10/8 = 1 (8). Sixteen (2 4 ) and more are not given by any factor, which means that the calculation can be completed. Summing up, we get that the exponent with two in the decomposition of 10! for prime factors will be 10/2 + 10/4 + 10/8 = 5 + 2 + 1 = 8.
If you act in the same way, you can find the indicators at 3, 5 and 7 in the decomposition of 10!, After which it remains only to calculate the value of the product:
ten! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
It remains to find the prime numbers from 2 to N, for this you can use the sieve of Eratosthenes :
static BigInteger FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; // List<Tuple<int, int>> p = new List<Tuple<int, int>>(); // for (int i = 2; i <= n; ++i) if (!u[i]) // i - { // int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } // p.Add(new Tuple<int, int>(i, c)); // int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } // BigInteger r = 1; for (int i = p.Count() - 1; i >= 0; --i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; } This implementation also takes about 0.9 seconds to compute 50,000!
GMP Library
As pomme rightly noted, the factorial calculation speed is 98% dependent on the speed of multiplication. Let's try to test our algorithms by implementing them in C ++ using the GMP library. The test results are given below, it turns out that the multiplication algorithm in C # has a rather strange asymptotics, so the optimization gives a relatively small gain in C # and a huge one in C ++ with GMP. However, this issue is probably worth a separate article.
Performance comparison
All algorithms were tested for N equal to 1,000, 2,000, 5,000, 10,000, 20,000, 50,000, and 100,000 with ten iterations. The table shows the average time in milliseconds.

Linear graph

Graph with logarithmic scale

Ideas and algorithms from comments
Habrazhiteli offered a lot of interesting ideas and algorithms in response to my article, here I will leave links to the best of them
lany parallelized the tree in Java using the Stream API and received acceleration 18 times
Mrrl proposed factoring optimization by 15-20%
PsyHaSTe proposed improving naive implementation
Krypt offered a parallelized version on C #
SemenovVV proposed implementation on Go
pomme suggested using GMP
ShashkovS proposed a fast Python algorithm.
Source codes
The source codes of the implemented algorithms are listed under the spoilers.
C #
using System; using System.Linq; using System.Text; using System.Numerics; using System.Collections.Generic; using System.Collections.Specialized; namespace BigInt { class Program { static BigInteger FactNaive(int n) { BigInteger r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } static BigInteger ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r - l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } static BigInteger FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } static BigInteger FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; bool[] u = new bool[n + 1]; List<Tuple<int, int>> p = new List<Tuple<int, int>>(); for (int i = 2; i <= n; ++i) if (!u[i]) { int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } p.Add(new Tuple<int, int>(i, c)); int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } BigInteger r = 1; for (int i = p.Count() - 1; i >= 0; --i) r *= BigInteger.Pow(p[i].Item1, p[i].Item2); return r; } static void Main(string[] args) { int n; int t; Console.Write("n = "); n = Convert.ToInt32(Console.ReadLine()); t = Environment.TickCount; BigInteger fn = FactNaive(n); Console.WriteLine("Naive time: {0} ms", Environment.TickCount - t); t = Environment.TickCount; BigInteger ft = FactTree(n); Console.WriteLine("Tree time: {0} ms", Environment.TickCount - t); t = Environment.TickCount; BigInteger ff = FactFactor(n); Console.WriteLine("Factor time: {0} ms", Environment.TickCount - t); Console.WriteLine("Check: {0}", fn == ft && ft == ff ? "ok" : "fail"); } } } C ++ with GMP
#include <iostream> #include <ctime> #include <vector> #include <utility> #include <gmpxx.h> using namespace std; mpz_class FactNaive(int n) { mpz_class r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } mpz_class ProdTree(int l, int r) { if (l > r) return 1; if (l == r) return l; if (r - l == 1) return (mpz_class)r * l; int m = (l + r) / 2; return ProdTree(l, m) * ProdTree(m + 1, r); } mpz_class FactTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } mpz_class FactFactor(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; vector<bool> u(n + 1, false); vector<pair<int, int> > p; for (int i = 2; i <= n; ++i) if (!u[i]) { int k = n / i; int c = 0; while (k > 0) { c += k; k /= i; } p.push_back(make_pair(i, c)); int j = 2; while (i * j <= n) { u[i * j] = true; ++j; } } mpz_class r = 1; for (int i = p.size() - 1; i >= 0; --i) { mpz_class w; mpz_pow_ui(w.get_mpz_t(), mpz_class(p[i].first).get_mpz_t(), p[i].second); r *= w; } return r; } mpz_class FactNative(int n) { mpz_class r; mpz_fac_ui(r.get_mpz_t(), n); return r; } int main() { int n; unsigned int t; cout << "n = "; cin >> n; t = clock(); mpz_class fn = FactNaive(n); cout << "Naive: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; t = clock(); mpz_class ft = FactTree(n); cout << "Tree: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; t = clock(); mpz_class ff = FactFactor(n); cout << "Factor: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; t = clock(); mpz_class fz = FactNative(n); cout << "Native: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl; cout << "Check: " << (fn == ft && ft == ff && ff == fz ? "ok" : "fail") << endl; return 0; } Source: https://habr.com/ru/post/255761/
All Articles