Magvik filter

Preface from the translator

Here is one of the newest methods for calculating the orientation in space according to the accelerometer, gyroscope and compass sensors — the Majwick filter, which, according to the author, gives better results than using a Kalman-based filter in results and performance. Author - Sebastian Madzhvik (his online store ). The method is described in the article in English. This work is protected at the University of Bristol Translation, I did not find. Translator from me so-so, especially such complex texts. But we are also interested in that method?

In some places I will add on my own - there the text is in italics . I found more than 10 misprints in the original text. In general, it was quite difficult, so help is welcome - write in the comments where you need to rephrase, in general, where something is wrong.

Filter data arrays of inertial and inertial magnetic sensors to determine the orientation

April 30, 2010
')

From the author

This article describes a new filter sensor readings for determining the orientation in space in two ways . The first option is applicable to inertial navigation systems (INS), including an accelerometer and gyroscope. The second option is applicable to ANNs, which include an additional 3-axis magnetometer ( abbreviation MARG - stands for “Magnetic, Angular Rate and Gravity” ). Implementing an ANN with a magnetometer involves compensating for magnetic distortion and compensating for the gyroscope offset. As a tool, quaternions are used, which allow the accelerometer and magnetometer data to be used for analytical calculations and optimization by the gradient descent method in obtaining the error of the gyroscope direction as a derived quaternion. Benefits include:

• low cost of computing resources - 277 simple arithmetic operations each filter update (109 operations without a magnetometer);
• efficiency at low sampling rates (for example 10 Hz);
• Contains 1 (without magnetometer) or 2 adjustable parameters, determined on the observed characteristics of the system.

Accuracy was evaluated empirically using commercially available orientation sensors. Reference orientation values ​​are obtained using an optical measurement system. A simple calibration method for using optical measuring equipment is presented in this paper.

Accuracy is also compared with a proprietary Kalman filter for orientation sensors. The results show that this filter reaches an accuracy level exceeding the filter based on the Kalman method:
<0.6 degrees standard deviation at rest;
<0.8 degrees standard deviation in a moving state.
As a result of low computational load and the ability to operate at low sampling rates, new opportunities for the use of ANNs for real-time devices with low computational capabilities and requirements for high sampling rates open up.

1. Introduction

Accurate determination of orientation in space plays an important role in many areas, including:

• Aerospace [1, 2, 3];
• Robotics [4, 5];
• Navigation [6, 7];
• Analysis of human movements [8, 9]
• The interaction of human and machine movements [10].

While various technologies can measure orientation, inertial sensor systems have the advantage of complete autonomy - the object being measured is not limited in movement, not limited to any particular environment or location. The inertial measurement unit ( BII, or from the English IMU - Inertial Measurement Unit ) consists of gyroscopes and accelerometers that allow you to track rotational and translational movements. In order to make 3D measurements, it is required that the sensor axes are mutually perpendicular. AGM is a hybrid BII, which includes a triaxial magnetometer. A system without a magnetometer can determine the orientation relative to the direction of gravity, which is sufficient for many applications [4, 2, 8, 1]. Inertial navigation systems use a reporting system known as “course, pitch, roll” (AHRS - Attitude and Heading Reference Systems) , and are able to provide a complete measurement of orientation relative to gravity and the earth's magnetic field.

The gyroscope measures the angular velocity, which, under known initial conditions, can be integrated over time to obtain the orientation of the sensor [11, 12]. Exact gyros, such as a ring laser, are too expensive and cumbersome for most applications. On the other hand, less accurate MEMS sensors (Micro Electrical Mechanical System - micromechanical electronic systems) are used in most applications [13]. Integration of measurement errors will lead to an accumulation of errors in orientation calculations. Thus, gyroscopes, by themselves, cannot provide an absolute measure of orientation. Accelerometer and magnetometer measure the gravitational and magnetic fields of our planet, and, accordingly, can determine the absolute value of orientation in space.

However, they are also likely to be exposed to high levels of noise. For example, acceleration due to movement will lead to a shift in the controlled direction of gravity. The task of the orientation filter is to calculate a single assessment of the orientation obtained by measuring the accelerometer, gyroscope and magnetometer.

The Kalman filter [14] has become the recognized basis for building most of the orientation determination algorithms [4, 15, 16, 17] and commercial orientation systems and inertial modules:

• xsens [18],
• Microstrain [19],
• VectorNav [20],
• InterSense [21],
• PNI [22],
• Crossbow [23],

- they are all based on its use. The widespread use of Kalman solutions are proof of their accuracy and efficiency, but they have several disadvantages. They can be difficult to implement, as shown in the available literature [3, 4, 15, 16, 17, 24, 25, 26, 27, 28, 29, 30, 31, 32]. Linear regression of iteration, is fundamental to the Kalman processes, the requirements for the sampling rate, significantly exceeding the capacity of the object. For example, a sampling frequency between 512 Hz and 30 kHz can be used in motion capture applications. The state of a relation describing rotating kinematics in three dimensions, as a rule, requires more state vectors and the implementation of an extended Kalman filter [4, 17, 24] for linearizing the problem.

These problems require a large computational load to implement Kalman solutions, but also to provide clear motives for the implementation of alternative approaches. Many previous approaches to solving these issues were based either on fuzzy processing [2, 5] or on fixing the filter [33] in favor of an accelerometer to determine orientation at low angular velocities and integrating gyro measurements when high angular velocities are detected. This approach is simple, but can be effective only under limited operating conditions. Bachmann and others [34] proposed an alternative approach in which the filter achieves an optimal synthesis of measurement data at all angular velocities. However, the process requires the least squares approximation, which also adds to the computational load. Mahoney and others [35] developed a complimentary filter, which, as practice shows, is an effective and efficient solution. However, accuracy is only suitable for ANNs without a magnetometer.

This article describes a new orientation filter that is applicable to an ANN without a magnetometer as well as to an ANN with a magnetometer. The filter is engaged in processing arrays of data received from sensors and eliminates the problems of accuracy and tuning of filter parameters based on Kalman approaches. The filter uses a quaternion to represent the orientation (for example [34, 17, 24, 30, 32]) to describe the position in space in three dimensions and does not contain problems associated with the description of the position by Euler angles (folding the frame). The article presents a complete conclusion and empirical evaluation of the new filter. Its accuracy is compared with existing industrial filters and verified by an optical measurement system. Innovative aspects of the proposed filter include:

• two adjustable parameters (one for implementation without a magnetometer) determined by the observed characteristics of the system;
• analytical calculations and optimization by the gradient descent method, which improves accuracy at low sampling rates;
• magnetic distortion compensation and gyroscope zero offset in real time.

2. Quaternions

This section of the article is not so interesting - it describes what a quaternion is and some basic operations. All this can be seen in the article with pictures . It is important for us to pay attention to the notation used by the author.

Fig. 1. The orientation of the axes B is achieved by rotating the axes A around the axis in report system A at an angle θ.

A quaternion is a four-dimensional complex number that can be used to represent the orientation of a pointed body or coordinates in three-dimensional space. It is possible to describe the orientation of the reporting system B with respect to the reporting system A by turning the angle θ around the axis in the report system A. This is depicted in Figure 1, where mutually orthogonal orths , and 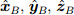defined by the main axis of the coordinate systems A and B, respectively. Quaternion describing this orientation defined by equation (1), where Rx, Ry and Rz are components of the vector in the corresponding X, Y, and Z axes of the report system A. For the naming of variables, report systems, and vectors, the notation used is the superscript and subscript indices according to Craig [37].

Ahead, the standing subscript indicates the target report system, and the ahead subscript indicates the reporting system with respect to which the variable is set. Further in the text, the S index denotes the sensor report system, and the E index the Earth report system. For example, describes the orientation of the B axes with respect to the A axes, and is a vector in the report system A. Quaternion arithmetic often requires that the quaternion be normalized to unity. Therefore, usually all quaternions describing the orientation have a length equal to one.



Please note - in this article, the W component of the quaternion goes first (it is often placed at the end).
Counterdirectional quaternions are denoted by * (asterisk) and are used to change the reporting system. for example opposed to * and describes the orientation of the reporting system A with respect to B. The opposite direction vector to determined by equation (2).



Quaternion resulting from the operation can be used to determine composite orientations (a series of turns) . For example, for two orientations and can be found according to the formula (3).



The result of multiplication for two quaternions a and b can be found using the Hamilton rule and is determined by formula (4). When changing places of factors, the result is different (multiplication of quaternions is associative, but not commutative).



A three-dimensional vector can be rotated to a quaternion using the relationship described in equation (5) [36]. and these are vectors in the coordinate systems A and B, respectively, where each vector contains 0 as a component of W, to make them 4 component vectors (quaternions) .


Orientation described by quaternion can be described as a rotation matrix determined by the formula (6) [36].



Euler angles ψ, θ and φ in the so-called aerospace sequence [36] describe the orientation of the axes achieved by successive rotations about the reporting system A, using the angle around the Z axis, θ around the Y axis, and φ around the X axis. Such Euler angles can be obtained from quaternion using equations (7), (8) and (9).

3. Filter

3.1. Orientation of angular velocity

A three-axis gyroscope measures the angular velocities ωx, ωy and ωz with respect to the axes X, Y, Z, respectively, in the sensor's report system. If the values ​​of these speeds (rad / sec) are converted to quaternion defined by equation (10), then a derived quaternion describing the velocity in the Earth’s reporting system with respect to the sensor’s reporting system can be calculated [38] by equation (11):


The orientation in the global reporting system with respect to the local sensor reporting system at time t is , can be calculated by numerical integration of quaternion derivatives , as described in equations (12) and (13), provided that the initial orientation in space is known.

Where - the angular velocity measured by the sensor at time t;
∆t is the delay between measurements (sampling period);
- previous result of orientation assessment.
The index ω indicates that the quaternion is calculated from angular velocities.

3.2. Orientation from vector observations

The three-axis accelerometer measures the magnitude and direction of the field of the local coordinate system along with linear accelerations due to the movement of the sensor. Similarly, a three-axis magnetometer measures the magnitude and direction of the earth’s magnetic field in a local reporting system along with local magnetic distortions. In the context of the orientation filter, at the initial moment of time it will assume that the accelerometer will measure only gravity, the magnetometer measures only the magnetic field of the Earth (the device must be stationary for a while) .

If the direction of the earth's field is known in its coordinate system, then measuring the direction in the coordinate system of the sensor will allow you to calculate the position of the coordinate system of the sensor relative to the coordinate system of the Earth. However, for any such measurement there will not be a single solution, but there will be an infinite number of solutions represented by all those orientations achieved by rotating the orientation around the rotation parallel to the field direction (magnetic or gravity) . In some cases, the solution can be represented in the form of Euler angles, where there will be two known angles and one unknown. An unknown angle will rotate around an axis parallel to the direction of the field. To represent a solution as a quaternion, a complex solution is required. This can be achieved by an optimization problem, where the sensor orientation this is what aligns the predefined field direction in the earth's coordinate system , with measured direction in sensor coordinate system using the rotation operation defined by equation (5). therefore can be found as a solution to equation (14), where equation (15) defines the objective function. The components of each vector are defined in equations (16), (17) and (18).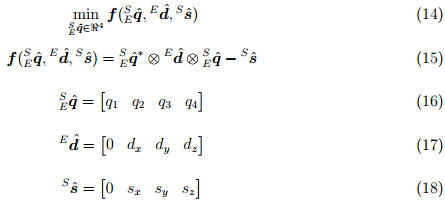

There are many optimization algorithms, but the gradient descent method is one of the simplest to implement and calculate. Equation (19) describes this method for n iterations as a result of an orientation estimate. based on "initial approximation" orientation and step size µ. Equation (20) calculates the gradient of the surface of the solutions defined by the objective function and its Jacobian , simplified to three-component vectors, defined in equations (21) and (22), respectively.


Equations (19) - (22) describe the general form of the algorithm applicable to the field, originally oriented in any direction. However, if the field direction can be considered only in one or two axes of the global coordinate system, the equation is simplified. The corresponding agreement will assume that the direction of gravity is directed vertically, along the Z axis, as shown in equation (23). Substituting the quaternion and normalized accelerometer measurements , and respectively, in equations (21) and (22) we obtain equation (25) and (26).


The direction of the earth's magnetic field can also be considered to be located in one plane and measured in the horizontal and vertical axes. The vertical component depends on the point on the globe in which the measurement takes place. For England, this value is between 65 and 70 degrees with respect to the horizon [39]. This can be represented by equation (27). Substituting and normalized measurement values , and respectively, in equations (21) and (22) we obtain equations (29) and (30).


As already discussed, the measurement of gravity or the magnetic field of the earth alone does not provide a unique sensor orientation. To do this, the measurements and directional relationships of both fields must be combined, as described in equations (31) and (32). While the surface of the solutions created by the objective functions in equations (25) and (29) have, at least, determined in accordance with the surface of the solutions defined by equation (31), and at least determined by one point, provided that .


The traditional approach to optimization will require several iterations of equation (19) to calculate the result for each new orientation and corresponding sensor measurements. Efficient algorithms also require step size μ to adjust the result at each iteration to the optimal value, usually derived from the second derivative of the objective function, Hesse. However, these requirements significantly increase the computational load of the algorithm and are not necessary in our business. It is acceptable for us to calculate one iteration per time count provided that the rate of convergence controlled by µt is equal to or greater than the physical rate of change of orientation. Equation (33) calculates the approximate direction calculated at time t based on previous orientation estimate and the objective function of the gradient ∇f determined by measuring the sensors and at time t. The shape ∇f is selected according to the sensors in use, as shown in equation (34). The index ∇ means that the quaternion is calculated using the gradient descent method.


The optimal value of µt can be defined as that which ensures the rate of convergence and is limited by the physical orientation speed, since it allows you to avoid exceeding due to excessively large step size. Therefore, µt can be calculated using equation (35), where ∆t is the time between measurements, Is the physical rate of change of orientation measured by the gyroscope; α is the increase in µ to account for noise when measured with an accelerometer and a magnetometer.

3.3. Algorithm of the uniting filter

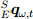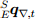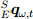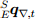We see that the orientation of the sensor in relation to the Earth is obtained by combining orientation calculations and calculated using equations (13) and (33), respectively. Union and described by equation (36), where γt and (1 - γt) are the weights applied to each orientation calculation.


The optimal value of γt can be defined as that at which the weighted divergence 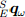equals weighted convergence . This is represented by equation (37), where Is the speed of convergence and β is the rate of divergence. 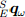, expressed as the quaternion value, derived from the corresponding measurement error of the gyroscope. Equation (37) can be modified to determine γt in equation (38).


Equations (36) and (38) provide the optimal combination. 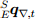and 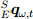provided that the rate of convergence α is regulated, which is greater than or equal to the physical rate of change of orientation. Therefore, α has no upper bound. If we assume that α is very large, then µt is determined by expression (35), and it also becomes very large values ​​in the simplified orientation filter equation. Large values ​​of µt used in equation (33) mean that becomes negligible and the equation can be rewritten in the form of expression (39).


Equation (38), which calculates γt, can be further simplified by taking the insignificance of β values ​​in the denominator and the expression can then be rewritten as equation (40). From equation (40), it is quite possible that γt ≈ 0.


Substituting equations (13), (39) and (40) into equation (36), we directly obtain equation (41). Note that γt in equation (41) is replaced both as expression (39) and as 0.


Equation (41) can be simplified to equation (42), where - this is the calculated rate of change of orientation, determined by the expression (43); Is the direction of the error determined by the expression (44).



From equations (42), (43) and (44), we see that the filter calculates the orientation by numerical integration of the estimated orientation speed . Filter computes as the rate of change of orientation measured by the gyroscope, the same, but still with the error of the measurement of the gyroscope, β - this is compensation in the direction of the alleged error; calculated on the basis of accelerometer and magnetometer measurements. Fig. 2 shows a block diagram of a complete implementation of an orientation filter for an ANN.


Fig. 2. Block diagram representing the complete implementation of the orientation filter for ANN

3.4. Magnetic distortion compensation

Measurements of the Earth’s magnetic field will be distorted by the presence of ferromagnetic sources near the sensor. Studies on the effect of magnetic distortions on the effectiveness of an orientation sensor showed that electrical appliances, metal furniture and metal structures used in the construction of buildings [40, 41] make a significant error. Interference sources in the sensor's report system can be compensated by its calibration [42, 43, 44, 45]. Interference sources in the Earth’s reporting system, such as those caused by iron deposits, cause errors in the controlled direction of the Earth’s magnetic field. Declination errors that are horizontal with respect to the earth's surface cannot be compensated without additional information about the course. Tilt errors in the vertical plane can be compensated for by the accelerometer, which provides an additional measurement relative to the sensor.

Controlled direction of the Earth’s magnetic field in terrestrial coordinates at time t, 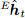can be calculated as the normalized measurement value of the magnetometer rotated by the orientation obtained by combining filter as described in equation (45). The effect of mistakenly tilting the magnetic field in the controlled direction of the Earth 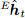can be corrected if the relative direction of the earth’s magnetic field all the time has the same slope. This is achieved by calculating the normals. and 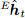only on the X and Y axes in the Earth’s reporting system, as described in equation (46).



Compensation of magnetic distortion in this case ensures that magnetic disturbances affect only the course. The approach also eliminates the need to preset the direction of the Earth’s magnetic field, which is a potential disadvantage of other approaches in orientation filters [17, 24].

3.5. Gyro zero drift compensation

The zero drift of the gyroscope will occur from changes in temperature, from movement, and simply with time. Any practical implementation of the INS should take this into account. The advantage of Kalman-like solutions is that they are able to estimate the gyroscope offset as an additional state within the framework of the system model [26, 30, 15, 24]. However, Mahoney et al. [35] showed that the zero drift of the gyroscope can also be compensated for by simple orientation filters, presenting it as part of the error of the orientation change rate. A similar approach will be used here.

The normalized direction of the calculated error in the rate of change of orientation can be expressed as the angular error along each axis of the gyroscope using equation (47) and is obtained as the inverse relation from equation (11). Gyro offset represented as a DC component and therefore can be removed since the part weighted average by the corresponding gain ζ. This compensates for the gyro measurement. 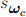as shown in equations (48) and (49). It is assumed that the first element 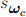always 0



Gyro compensated measurements 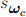can be used instead of the original gyro measurements in equation (11). The magnitude of the angular error in each axis equal to the quaternion of unit length. Therefore, the built-in gain ζ directly determines the rate of convergence of the expected gyroscope bias expressed as a derived quaternion. Since this process requires a complete assessment of the filter orientation. this applies only to the implementation of a filter with a magnetometer. Fig. 3 shows a block diagram of a representation of a full filter implementation for an ANN with a magnetometer, including compensation for magnetic distortion and gyroscope drift.


Fig. 3. A block diagram representing the complete INS filter with a magnetometer including magnetic distortion compensation (group 1) and gyro drift compensation (group 2).

3.6. Filter gains

The gain of the filter β represents all the measurement errors of the gyroscope zero, expressed as the value of the derived quaternion. Sources of error: sensor noise, smoothing filter, quantization errors, calibration errors, sensor alignment and sensor alignment errors, non-orthogonal sensor axes, and frequency characteristics. The filter gain ζ is the convergence rate for removing gyro measurement errors that are not related to zero and is also expressed as the value of the derived quaternion. These errors represent the gyroscope offset. It is convenient to determine β and ζ using angular values and accordingly, where represents an estimate of the average measurement error of zero on each axis, and represents the calculated drift velocity of the gyroscope in each axis. Using the relationship described by equation (11), β can be defined by equation (50), where represents every single quaternion. Similarly, ζ can be described using equation (51).

4. Testing

4.1 Equipment

The filter was tested using the xsens MTX orientation sensor unit [18], containing a 16-bit three-axis: gyroscope, accelerometer and magnetometer. The device and associated software use an operation mode where raw sensor data is received at a frequency of 512 Hz and then processed to provide calibrated sensor measurements. Calibrated sensor measurements can be processed using the proposed filter to ensure the calculated orientation of the sensor. The software also includes the computation of an additional estimation of the orientation with a Kalman-like filter. Both filters - Calman-like and proposed, can work using the same sensor output data. The accuracy of each algorithm is evaluated with respect to each other as the accuracy of independent sensors.

The Vicon system, consisting of 8 MX3 + cameras, connected to the MXultranet [46] server and Nexus [47] software was used to provide reference measurements of the actual orientation of the orientation sensor. The system of the array of IR (infrared) sensitive cameras with included IR illuminators. Cameras are fixed on calibrated positions and orientations so that the object of measurement is in the field of view of several cameras. The Cartesian positions of IR reflecting optical markers attached to the measurement object can be calculated in the coordinate system of the camera array. The cameras were installed at a height of approximately 2.5 m and were evenly distributed around the perimeter of the site 4 m by 4 m. Each camera was oriented towards the center of the room, approximately from 30◦ to 60◦ to the horizontal. The experiments were carried out with the object of measurement in the center of the room at a height of about 1 m. To measure the orientation of the sensor, it was attached to an optical orientation measurement platform specially designed for this experiment. The system was used to record the positions of optical markers with a speed of 120 Hz.

4.2 Determination of orientation from optical measurements

The orientation measurement platform consists of 3.5 m, mutually orthogonal rods rigidly connected in the center. Optical markers are fixed at each end of the rod and a platform with an orientation sensor is fixed at their intersection. The platform was made of aluminum, carbon fiber rods and all assembled using adhesives to ensure that the structure did not have magnetic properties that could interfere with the magnetometer. Additional optical markers were placed in arbitrary positions along the length of the rods breaking the axial symmetry in order to help identify each bar in a given dimension. In fig. 4 shows a photograph of the orientation measurement platform, where , ,
, , and - this is the measured position of each frame marker within the visibility of the camera. These positions can be used to define 3 mutually orthogonal vectors. , and in the coordinate system of the camera, getting the directions of the axes of the platform X, Y, Z so. as shown in equations (52), (53) and (54). These vectors define a rotation matrix that describes the orientation of the measurement platform in the camera's coordinate system, as shown in equation (55).


Fig. 4. Photo of orientation measurement platform



Due to measurement errors and tolerances in the frame with markers, the rotation matrix defined by equation (55) cannot be considered orthogonal and therefore does not constitute pure rotation. Bar-Yitzhak presents us with method (48), where, according to the optimal “best fit,” a quaternion can be extracted from a non-exact and non-orthogonal rotation matrix. The method requires the construction of a 4x4 symmetric matrix, K , defined by equation (56), where matches the mth row of the nth column . Optimal Quaternion is found as a normalized eigenvector corresponding to the maximum eigenvalue of the matrix K. Equation (57) defines the optimal alternative. Equation (57) determines the optimal alternative quaternion, as conventionally assumed by the method, where V1, V2, V3 and V4 define the elements of the normalized eigenvector .

4.3 Calibration of the combination of report systems

In order to compare the optical measurements of the orientation of the platform in the frame of the camera, , and the proposed filter orientation relative to the Earth, , it is required to know the alignment of the Earth’s reporting system with respect to the camera’s reporting system, , and alignment of the measuring platform, relative to the sensor report system . Once these values ​​have been found, the optical measurement of the orientation of the sensor in the Earth’s reporting system, , is determined by the formula (58).Although the use of optical equipment is described in the annexes to documents [26, 24, 41], there is a proposal to discuss a little about the calibration of these two quantities.


The X and Z axes of the Earth’s reporting system are determined by its magnetic field and gravity. Measurement of these fields in the camera report system can be used to align .The direction of gravity is determined using a thread with a weight (pendulum) with a length of 1 meter attached to the platform. The optical marker is placed on the weight and the end of the wobble is reached , i.e. the weight is brought to a stationary state .

An additional optical marker is required at an arbitrary fixed location relative to a static pendulum (weight) in order to break the axial symmetry of the “constellation” of optical markers. Fig. 5 shows a commented photo of the pendulum, where and determine the position of markers in the camera's report system. The average position of each marker for a certain period of time determines the direction of the pendulum in the camera’s reporting system, .This directly determines the Z axis of the Earth’s reporting system in the camera’s reporting system , as shown in equation (59).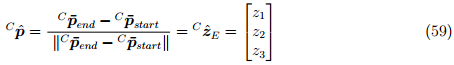




Fig.5: Photograph of a pendulum and optical markers used to measure the direction of gravity in the camera’s reporting system The

direction of the earth’s magnetic field was measured using a magnetic compass made from a meter-long carbon fiber rod with neodymium magnets attached to each end. The direction of the north and south poles of the magnets is the same. The compass is suspended on a cotton thread and brought to rest. Optical markers are placed at the ends of the rod, as well as asymmetrically elsewhere along the rod, in order to break the axial symmetry of the “constellation” (probably to identify each end) . In fig. 6 shows a commented photograph of the compass, where and I determine the position of optical markers in the camera's report system. The average position of each marker over a period of time determines the position of the compass in the camera's reporting system , as shown in expression (60).


Figure 6: Photograph of a magnetic compass and optical markers used to measure the direction of the Earth’s magnetic field in the camera’s reporting system



Due to measurement errors and an imbalance of a suspended magnetic compass, it cannot be considered orthogonal towards gravity defined as and therefore cannot be used for direct determination of the X axis of the Earth. Non-orthogonality can be calculated as a projection on the axis .This component can be removed from to determine the direction of the X-axis of the Earth in the camera's reporting system , as shown in expression (61). After normalization, we obtain the X axis of the Earth,, as shown in expression (62).



The Y axis of the Earth’s reporting system in the camera’s reporting system can be calculated as the perpendicular to and , as defined in equation (63) and where the signs are chosen so that the direction of the axes is consistent with the agreement (meaning the right and left coordinate systems) . The alignment of the terrestrial reporting system can be defined as a rotation matrix constructed from , and .The quaternion representation can be obtained by the method of Bar-Yitzchak [48].



In order to find the alignment , it is assumed that the static error of the filter based on the Kalman method is equal to zero on average. The average output was calculated by measuring the platform, which is stationary for about 10 seconds. This was used with alignment and optical measurement to determine the alignment of the platform in the sensor report system , as defined in expression (65).

4.4. The procedure for conducting experiments

Optical measurement data and raw orientation sensor data were recorded simultaneously. Then, the raw data of the orientation sensors were processed by an appropriate program to calibrate the sensor data and the filter output based on Kalman. This data is then synchronized with the data of optical measurements, while the data of optical measurements are interpolated due to the higher frequency of measurements of orientation sensors. Then the calibrated sensor data is processed using both variants of the proposed method: with and without a magnetometer. Optical data is extracted by the methods described in 4.2 and 4.3.

The gain β of the proposed filter was set to 0.033 for implementation without a magnetometer and 0.041 for implementation with a magnetometer. The generalizations from section 5.3 show that the coefficients found provide maximum accuracy. However, during the first 10 seconds, a factor of 2.5 was used to ensure the convergence of the algorithm under the initial conditions.

Gain ζ, applicable only to the version with a gyroscope, was set to 0, since the calibration of orientation sensors does not imply a gyroscope bias drift.

Data was obtained for a sequence of turns made by hand. The measurement platform is at rest for 20-30 seconds to allow the algorithm to stabilize time. Then the platform is rotated 90◦ around its axis X, and then 180◦ in the opposite direction, and then it is rotated 90◦ to bring the platform to its original position. The platform between each rotation is held stationary for 3 to 5 seconds. This sequence is then repeated for the Y and Z axes. The peak of the angular velocity measured during each turn ranged from 110◦ / s to 190◦ / s. The experiment was repeated 8 times to get an idea of ​​the accuracy of the system.

5. Results

Among the generally accepted methods for quantifying the characteristics of the orientation filter [24, 26, 18, 19, 20, 21], we see the root-mean-square errors in the mobile (dynamic) and stationary (static) states apart from Euler angles describing the course, roll, pitch. The pitch φ, roll θ and heading ψ correspond to rotation around the X, Y, Z axes, respectively, in the sensor report system. The corners mentioned above are detached from Euler angles and can be more easily interpreted and visualized. The disadvantage of the Euler angles is that they do not describe the relationship between the parameters, and they are also subject to large unstable errors when the values ​​of some angles reach the poles.

Euler angles were calculated directly from the resulting quaternion using equations (7), (8) and (9).
In total, 4 sets of Euler parameters were calculated, they correspond to calibrated optical orientation measurements, orientation estimation by the filter based on the Kalman method, and the proposed orientation estimation filter for implementations with and without a sensor. The errors of the estimated Euler parameters: φ, θ and ψ, were calculated as the difference between the Euler parameters of the calibrated optical measurements and the corresponding parameters at the output of the filter.

5.1. Average results

In fig.7, 8 and 9 show the average results for 8 experiments for both the filter based on the Kalman method and the proposed implementation of the filter with a magnetometer. In each figure there are 3 graphics. The upper plot represents the optically measured angle. Further, the angle estimate by the filter based on the Kalman method, and finally the angle estimate by the represented filter. The two graphs below represent the calculated error in each of the proposed angles.


Figure 7. Average results of measurements and estimates of the angle φ (above) and estimation errors (below)


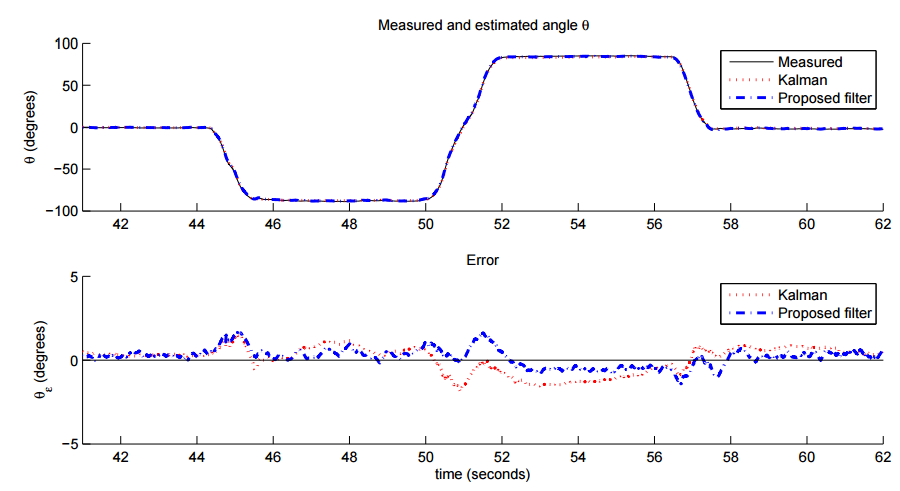
Figure 8. Average results of measurements and estimates of the angle θ (above) and estimation errors (below)


Figure 9. Average results of measurements and estimates of the angle (above ) and evaluation errors (below)

5.2. Static and dynamic characteristics

Standard deviations of angles , and were calculated on the assumption that the angular velocity in the stationary state was <5 / s, and in the moving state ≥ 5 / s.

This threshold was chosen to be high enough relative to the noise level of the input data. Each value of the standard deviation was calculated in the time interval in which the corresponding Euler angle was rotated, as shown in Fig. 7, 8 and 9. This was done in order to prevent errors due to the initial convergence or features in the representation of Euler angles, that is, when θ = ± 90 (talking about folding the frame ) . The results are shown in Table 1. Each value represents the average of all 8 experiments. The values ​​of the standard deviationwere not calculated for implementation without a magnetometer, since this implementation is not intended to accurately determine the course and cannot compensate for the accumulation of errors in this parameter.


Table 1. Standard deviations for filters: based on the Kalman method and the proposed method in realizations with and without a magnetometer

The results show that the proposed filter achieves higher accuracy than the filter based on the Kalman method. Orientation sensor manufacturers indicate average deviations of filters based on the Kalman method in the range <0.5◦ for the angles φ and θ and <1◦ for [18]. These values ​​do not correspond to those given in Table 1. Other studies [49] showed that the accuracy can be significantly lower than those given by the manufacturers and that the level of accuracy indicated by them is achieved only during calibration. The low accuracy levels in heading measurement are caused by the low level of sensor accuracy in measuring the Earth’s magnetic field. The slope of the Earth’s magnetic field during testing was between 65 ° and 70 ° with respect to the horizon [39]. As a consequence, the component of the flux vector for determining the course is relatively small. The larger component of the vector,along with the measurement of gravity, serves as an additional criterion for determining the roll θ and pitch φ. Hence the standard deviation of pitchand roll will be less than the course .The magnetometer, as indicated in [18], has a bandwidth of 10 Hz, which, compared with the bandwidth of the accelerometer and gyroscope, which ranges from 30 to 40 Hz, also implies an increased error in determining the course in a stationary state.

5.3. The effect of filter gain on accuracy

The results of the study of the effect of the gain β on the filter accuracy are displayed as a graph in Fig. 10. The experimental data were processed by limiting β values ​​between 0 and 0.5. Each filter implementation has its own optimal value β, which is high enough to compensate for the accumulation of errors and low enough so that unnecessary noise does not fall into large steps of the gradient descent.


Fig. 10. The effect of filter gain β on accuracy

5.4. The effect of measurement frequency on accuracy

In fig.11 presents the results of a study of the effect of the measurement frequency on the filter accuracy. The experiments were carried out using the optimal value of the gain β for both realizations (with and without a magnetometer). The change in the frequency of measurements was simulated by skipping part of the measurements and ranged from 1 Hz to 512 Hz. From fig. 11 it can be seen that the proposed filter achieves the same level of accuracy at a sampling frequency of 50 Hz, as at a frequency of 512 Hz. Both implementations of the filter achieve a reduction in static error (in a stationary state) <2 and dynamic error (in the moving state of the platform) <7◦ already at a sampling frequency of 10 Hz. This level of accuracy is sufficient for use in human capture applications.


Fig. 11. Effect of measurement frequency on filter accuracy for implementations with and without a magnetometer

5.5. Gyro zero drift

The calibrated gyro data used in the proposed filter does not contain any bias errors. In order to investigate the ability of the proposed filter to offset drift compensation, errors were artificially entered into the data of all 8 experiments. A constant drift of 0.2◦ / s / s was added to the measurements of the gyroscope on the X axis and a constant bias error of −0.2 / s / s to the measurements of the gyroscope on the Y axis .The gain ζ was set to 0 for the first 10 seconds during each experiment, while the filter converged with the initial conditions. After that, the value was set to 0.015 as the corresponding maximum gyroscope displacement rate of 1◦ / s / s. Fig. 12 shows the average results of 8 experiments, showing the gyro zero offset according to the filter estimates from the actual position along the gyroscope axes X and Y. The filter accuracy under these conditions is described in table 1.


Fig. 12 Tracking gyro zero drift filter

6. Discussion

At the beginning of work on the filter, it was assumed that the accelerometer and magnetometer would measure only the force of gravity and the magnetic field of the Earth. In practice, due to the acceleration of the movement, this leads to an erroneous observed direction of gravity (especially if the overload created by the movement is commensurate or more than the magnitude of the force of gravity), which gives a potentially incorrect estimate of the height, and the distortion of the magnetic field gives an incorrect estimate of the course. In many filter implementations, the authors make the assumption that the acceleration of motion and magnetic distortion are present only for a short period of time. Therefore, the magnitude of the filter gain β can be chosen low enough so that the deviation caused by erroneous ideas about the gravitational and magnetic distortions observed in the field is reduced to an acceptable level for the period. The minimum allowable value of β is limited by the measurement accuracy of the gyroscope.

In many applications, it may be useful to use the dynamic increment of β and β values. This will reduce the effect of the accelerometer or magnetometer on the assessment of the current position during problem periods, for example, when a large overload is detected. Using large filter gains during initialization can also improve filter convergence in initial conditions. For example, it was found that increasing β and ζ by 10 allows for 5 seconds from the moment the filter was turned on to compensate for the gyroscope bias error of 1000 degrees / s in each axis.

The filter structure for the installation of an INS sensor array with a magnetometer is similar to that proposed by Bachmann and others [34]. Both implementations of the filter estimate the measurement error of the gyroscope as the gradient of the error surface created by the measurements of the accelerometer and the magnetometer. The Bachmann filter calculates this using the Gauss-Newton approach, which requires numerical differentiation and matrix inversion. The filter proposed in this report uses Jacobi’s analytical derivation and works on a normalized error surface gradient. As a result, the filter proposed in this article provides for a significant reduction in the computational load and allows the filter to optimally amplify the source based on the observed characteristics of the system.

The experimental procedure used to assess the accuracy of the filter has several limitations. The filter was not evaluated for simultaneous rotation around more than one axis and rotation speeds were limited in magnitude and time. These limitations were necessary for repeatability and quantification to be possible.

7. Conclusions

Essentially the repetition of the text from the introduction.

Appendix A. Implementing a filter on C without a magnetometer

The following source code is an implementation of an orientation filter without a magnetometer. C-code has been optimized to minimize the required number of arithmetic operations due to RAM. Each filter update requires 109 scalar arithmetic operations (18 addition operations, 20 subtractions, 57 multiplications, 11 divisions and 3 square root). The implementation requires 40 bytes of RAM for global variables and 100 bytes of RAM for local variables during each call filter update functions.

Appendix A. Implementing a C filter with a magnetometer

The following source code is an implementation of an orientation filter with a magnetometer and a gyroscope drift compensation system. C-code has been optimized to minimize the required number of arithmetic operations due to RAM. Each filter update requires 277 scalar arithmetic operations (51 addition operations, 57 subtractions, 155 multiplications, 14 divisions and 5 square root derivations). The implementation requires 72 bytes of RAM for global variables and 260 bytes of RAM for local variables during each call filter update functions.

Bibliography

1. Mark Euston, Paul Coote, Robert Mahony, Jonghyuk Kim, and Tarek Hamel. A fixed-wing filter with a low-cost imu. In 6th International Conference on Field and Service Robotics, July 2007.
2. Sung Kyung Hong. Fuzzy logic based closed-loop strapdown attitude system for unmanned aerial vehicle (uav). Sensors and Actuators A: Physical, 107(2):109 – 118, 2003.
3. A. Kallapur, I. Petersen, and S. Anavatti. A robust gyroless attitude estimation scheme for a small fixed-wing unmanned aerial vehicle. pages 666 –671, aug. 2009
4. B. Barshan and HF Durrant-Whyte. Inertial navigation systems for mobile robots. 11(3):328–342, June 1995.
5. L. Ojeda and J. Borenstein. Flexnav: fuzzy logic expert rule-based position estimation for mobile robots on rugged terrain. In Proc. IEEE International Conference on Robotics and Automation ICRA '02, volume 1, pages 317–322, May 11–15, 2002.
6. David H. Titterton and John L. Weston. Strapdown inertial navigation technology. The Institution of Electrical Engineers, 2004.
7. S. Beauregard. Omnidirectional pedestrian navigation for first responders. In Proc. 4th Workshop on Positioning, Navigation and Communication WPNC '07, pages 33–36, March 22–22, 2007.
8. HJ Luinge and PH Veltink. Inclination measurement of human movement using a 3-d accelerometer with autocalibration. 12(1):112–121, March 2004. [9] Huiyu Zhou and Huosheng Hu. Human motion tracking for rehabilitation–a survey. volume 3, pages 1 – 18, 2008.
9. EA Heinz, KS Kunze, M. Gruber, D. Bannach, and P. Lukowicz. Using wearable sensors for real-time recognition tasks in games of martial arts — an initial experiment. In Proc. IEEE Symposium on Computational Intelligence and Games, pages 98–102, May 22–24, 2006.
10. JE Bortz. A new mathematical formulation for strapdown inertial navigation. (1):61– 66, January 1971.
11. MB Ignagni. Optimal strapdown attitude integration algorithms. In Guidance, Control, and Dynamics, volume 13, pages 363–369, 1990.
12. N. Yazdi, F. Ayazi, and K. Najafi. Micromachined inertial sensors. 86(8):1640–1659, August 1998.
13. RE Kalman. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 82:35–45, 1960.
14. E. Foxlin. Inertial head-tracker sensor fusion by a complementary separate-bias kalman filter. In Proc. Virtual Reality Annual International Symposium the IEEE 1996, pages 185–194,267, March 30–April 3, 1996.
15. HJ Luinge, PH Veltink, and CTM Baten. Estimation of orientation with gyroscopes and accelerometers. In Proc. First Joint [Engineering in Medicine and Biology 21st Annual Conf. and the 1999 Annual Fall Meeting of the Biomedical Engineering Soc.] BMES/EMBS Conference, volume 2, page 844, October 13–16, 1999.
16. JL Marins, Xiaoping Yun, ER Bachmann, RB McGhee, and MJ Zyda. An extended kalman filter for quaternion-based orientation estimation using marg sensors. In Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems, volume 4, pages 2003–2011, October 29–November 3, 2001.
17. Xsens Technologies BV MTi and MTx User Manual and Technical Documentation. Pantheon 6a, 7521 PR Enschede, The Netherlands, May 2009.
18. MicroStrain Inc. 3DM-GX3 -25 Miniature Attutude Heading Reference Sensor. 459 Hurricane Lane, Suite 102, Williston, VT 05495 USA, 1.04 edition, 2009.
19. VectorNav Technologies, LLC. VN -100 User Manual. College Station, TX 77840 USA, preliminary edition, 2009.
20. InterSense, Inc. InertiaCube2+ Manual. 36 Crosby Drive, Suite 150, Bedford, MA 01730, USA, 1.0 edition, 2008.
21. PNI sensor corporation. Spacepoint Fusion. 133 Aviation Blvd, Suite 101, Santa Rosa, CA 95403-1084 USA.
22. Crossbow Technology, Inc. AHRS400 Series Users Manual. 4145 N. First Street, San Jose, CA 95134, rev. c edition, February 2007.
23. AM Sabatini. Quaternion-based extended kalman filter for determining orientation by inertial and magnetic sensing. 53(7):1346–1356, July 2006.
24. HJ Luinge and PH Veltink. Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Medical and Biological Engineering and Computing, 43(2):273–282, April 2006.
25. David Jurman, Marko Jankovec, Roman Kamnik, and Marko Topic. Calibration and data fusion solution for the miniature attitude and heading reference system. Sensors and Actuators A: Physical, 138(2):411–420, August 2007.
26. Markus Haid and Jan Breitenbach. Low cost inertial orientation tracking with kalman filter. Applied Mathematics and Computation, 153(4):567 575, June 2004.
27. D. Roetenberg, HJ Luinge, CTM Baten, and PH Veltink. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. 13(3):395–405, September 2005.
28. John L. Crassidis and Landis F. Markley. Unscented filtering for spacecraft attitude estimation. Journal of guidance, control, and dynamics, 26(4):536–542, 2003.
29. D. Gebre-Egziabher, RC Hayward, and JD Powell. Design of multi-sensor attitude determination systems. Aerospace and Electronic Systems, IEEE Transactions on, 40(2):627 – 649, april 2004.
30. NHQ Phuong, H.-J. Kang, Y.-S. Suh, and Y.-S. Ro. A DCM based orientation estimation algorithm with an inertial measurement unit and a magnetic compass. Journal of Universal Computer Science, 15(4):859–876, 2009.
31. Daniel Choukroun. Novel methods for attitude determination using vector observations. PhD thesis, Israel Institute of Technology, May 2003.
32. RA Hyde, LP Ketteringham, SA Neild, and RJS Jones. Estimation of upperlimb orientation based on accelerometer and gyroscope measurements. 55(2):746–754, February 2008.
33. ER Bachmann, I. Duman, UY Usta, RB McGhee, XP Yun, and MJ Zyda. Orientation tracking for humans and robots using inertial sensors. In Proc. IEEE International Symposium on Computational Intelligence in Robotics and Automation CIRA
34. '99, pages 187–194, November 8–9, 1999.
35. R. Mahony, T. Hamel, and J.-M. Pflimlin. Nonlinear complementary filters on the special orthogonal group. Automatic Control, IEEE Transactions on, 53(5):1203 –1218, june 2008.
36. JB Kuipers. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality. Princeton University Press, 1999.
37. John J. Craig. Introduction to Robotics Mechanics and Control. Pearson Education International, 2005.
38. David R. Pratt Robert B. McGhee Joseph M. Cooke, Michael J. Zyda. Npsnet: Flight simulation dynamic modelling using quaternions. Presence, 1:404–420, 1994.
39. John Arthur Jacobs. The earth's core, volume 37 of International geophysics series. Academic Press, 2 edition, 1987.
40. ER Bachmann, Xiaoping Yun, and CW Peterson. An investigation of the effects of magnetic variations on inertial/magnetic orientation sensors. In Proc. IEEE International Conference on Robotics and Automation ICRA '04, volume 2, pages 1115–1122, April 2004.
41. CTM Baten FCT van der Helm WHK de Vries, HEJ Veeger. Magnetic distortion in motion labs, implications for validating inertial magnetic sensors. Gait & Posture, 29(4):535–541, 2009.
42. Speake & Co Limited. Autocalibration algorithms for FGM type sensors. Application note.
43. Michael J. Caruso. Applications of Magnetoresistive Sensors in Navigation Systems. Honeywell Inc., Solid State Electronics Center, Honeywell Inc. 12001 State Highway 55, Plymouth, MN 55441.
44. JF Vasconcelos, G. Elkaim, C. Silvestre, P. Oliveira, and B. Cardeira. A geometric approach to strapdown magnetometer calibration in sensor frame. In Navigation, Guidance and Control of Underwater Vehicles, volume 2, 2008.
45. Demoz Gebre-Egziabher, Gabriel H. Elkaim, J. David Powell, and Bradford W. Parkinson. Calibration of strapdown magnetometers in magnetic field domain. Journal of Aerospace Engineering, 19(2):87–102, 2006.
46. Vicon Motion Systems Limited. Vicon MX Hardware. 5419 McConnell Avenue, Los Angeles, CA 90066, USA, 1.6 edition, 2004.
47. Vicon Motion Systems Limited. Vicon Nexus Product Guide — Foundation Notes. 5419 McConnell Avenue, Los Angeles, CA 90066, USA, 1.2 edition, November 2007.
48. Itzhack Y Bar-Itzhack. New method for extracting the quaternion from a rotation matrix. AIAA Journal of Guidance, Control and Dynamics, 23(6):10851087, Nov.Dec 2000. (Engineering Note).
49. MA Brodie, A. Walmsley, and W. Page. The static accuracy and calibration of inertial measurement units for 3D orientation. Computer Methods in Biomechanics and Biomedical Engineering, 11(6):641–648, December 2008.