Top 100+ Wolfram | Alpha Sine Functions, or Wolfram | Alpha Overview of Mathematical Features and Syntax

Translation of post by Michael Trott and Eric W. Weisstein "by Michael Trott & Eric W. Weisstein
The Top 100+ Sines of Wolfram | Alpha ", significantly expanding the issues raised by the authors.
Download the translation in the form of a Mathematica document that contains all the code used in the article here (archive, ~ 12 MB).

The Wolfram | Alpha service can perform a huge number of various calculations and mathematical calculations are one of its narrow specialties. In fact, using the power of Mathematica's computational capabilities, which created Wolfram | Alpha, Wolfram | Alpha can solve a wide range of tasks related to mathematical functions, ranging from the simplest to the devilishly complex.

To clarify what we mean by “a large range of tasks” (about which we really think so), let us take as an example such an unassuming mathematical function as sine. Below, we have provided a list that reveals 93 possibilities that Wolfram | Alpha can do with a sine, but in the end we added a number of bonus features that we couldn’t resist.
')
Let's start by simply entering a request sin (x) into Wolfram | Alpha, i.e., just the sine function of the argument x, as it is. The following is what Wolfram | Alpha will give us as a result for this request:

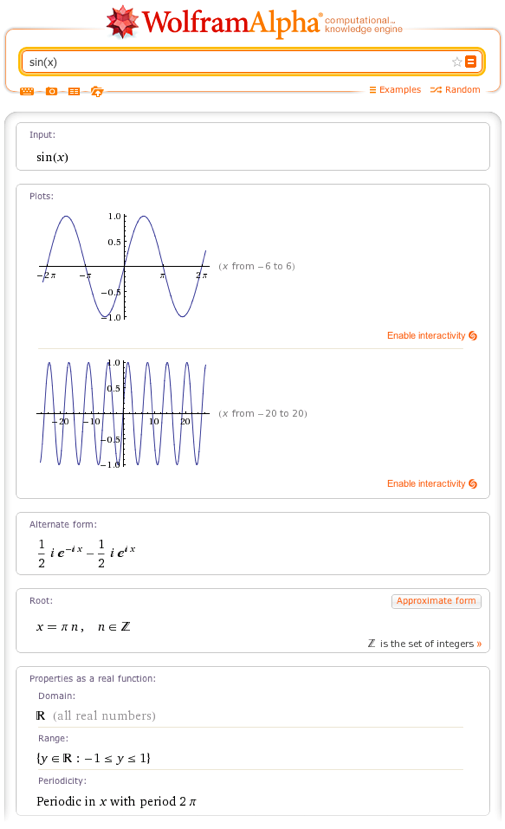
For those who know what real numbers are, most of the above results refer to the actual values of the argument x. On the other hand, if you use a different kind of argument for the sine function, that is, enter a query, say, sin (z) or sin (x + iy) , then Wolfram | Alpha will assume that you want to work in the field of complex numbers ( complex variables) and will give you a different set of graphs and results, as shown in the figure below:

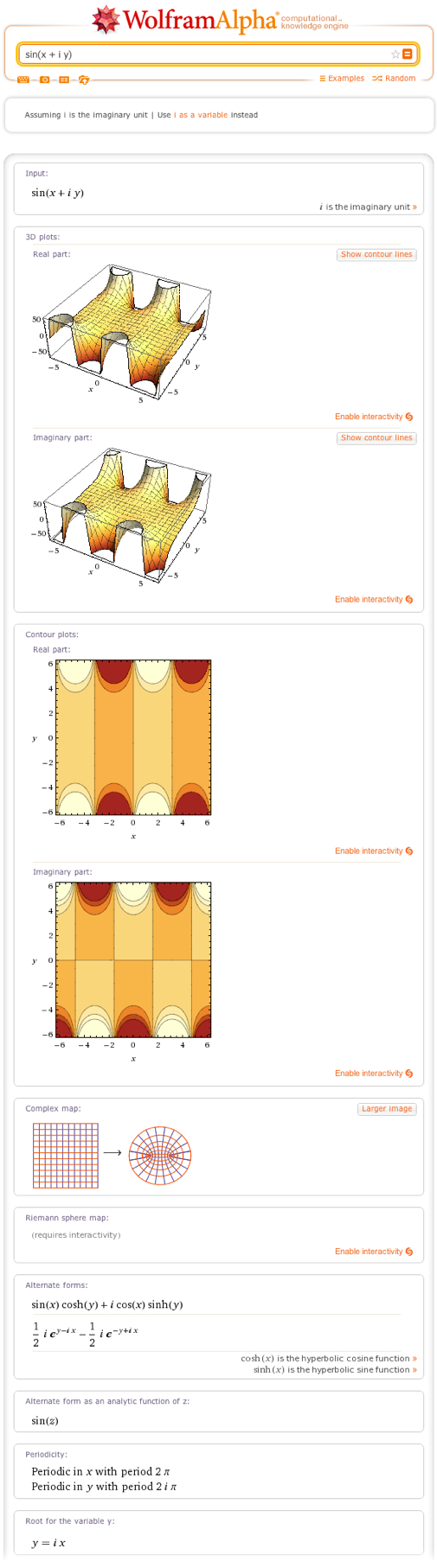
Of course, you can ask Wolfram | Alpha to calculate each of the above calculation results separately, for example,

• The global maximum of the sin (x) function .

Wolfram | Alpha : global maxima sin (x) query

Wolfram Language (Mathematica) Code :

You can also build a lot of graphs by specifying the corresponding queries:

• Build sin (x), sin (2x), sin (3x) plots

Wolfram | Alpha Query : Plot sin (x), sin (2x), sin (3x)

Wolfram Language (Mathematica) Code :

• Build charts sin (x), sin (sin (x)), sin (sin (sin (x))), sin (sin (sin (sin (x))), sin (sin (sin (sin (sin) (x)))))

Request Wolfram | Alpha : Plot sin (x), sin (sin (x)), sin (sin (sin (x))), sin (sin (sin (sin (x))), sin (sin (sin (sin (sin (x)))))

Wolfram Language (Mathematica) Code :

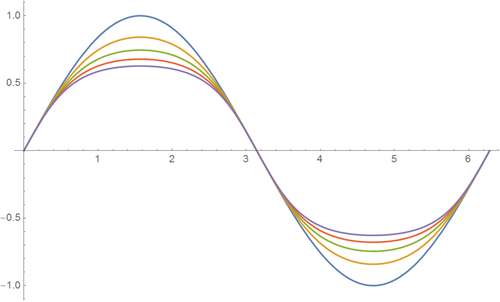
• Graph of isolines of the surface sin (x / | y | - y / | x |) at x = -π to π and y = -π to π

Wolfram | Alpha query : Contourplot sin (x / | y | - y / | x |) from x = -pi to pi and y = -pi to pi

Wolfram Language (Mathematica) Code :

• Surface graph sin (x - y) / sin (x + y) with x = -2π to 2π and y = -2π to 2π

Wolfram | Alpha query : Plot3d sin (x - y) / sin (x + y) from x = -2pi to 2pi and y = -2pi to 2pi

Wolfram Language (Mathematica) Code :

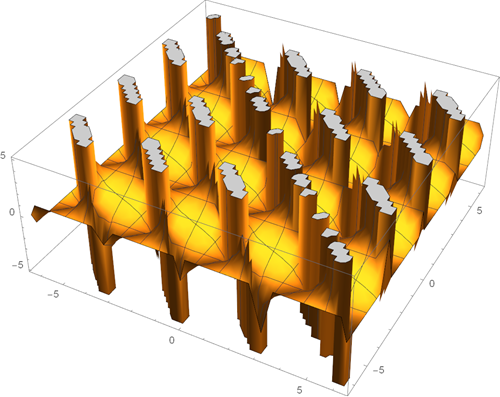
• Polar plot r = 1 + sin (100 θ)

Wolfram | Alpha query : Polar plot r = 1 + sin (100 theta)

Wolfram Language (Mathematica) Code :

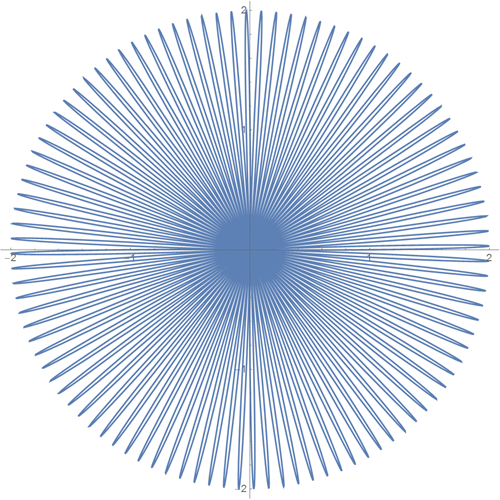
The result of the last query received in Wolfram | Alpha is:

You can also easily build more complex expressions depending on the sine function, for example:

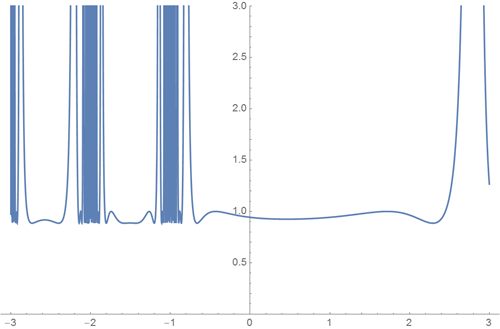
• Graph of the function {(1 / {1 / sin (x)}} , where {y} is the fractional part of the number y.

Wolfram | Alpha : Plot frac request (1 / frac (1 / sin (x)))

Wolfram Language (Mathematica) Code :

• Graph of the function sin (x!)! at x = -3 to 3

Request Wolfram | Alpha : Plot sin (x!)! from x = -3 to 3

Wolfram Language (Mathematica) Code :

• Graphically represent the terms of the sequence 1, sin (1), sin (sin (1)), ... (total 101 members)

Request Wolfram | Alpha : Plot nestlist (sin, 1., 100)

Wolfram Language (Mathematica) Code :

• Graph of a parametrically given curve x = max (sin (t), cos (pi t)), y = max (cos (t), sin (pi t))} t = 0 to 100

Request to Wolfram | Alpha : Parametric plot {max (sin (t), cos (pi t)), max (cos (t), sin (pi t))} from t = 0 to 100

Wolfram Language (Mathematica) Code :

• Graphs of the surface of the real and imaginary parts of the function sin (sin (x + iy)) with x = -π to π and y = -π to π

Request Wolfram | Alpha : Plot3d sin (sin (x + iy)) from x = -pi to pi and y = -pi to pi

Wolfram Language (Mathematica) Code :

• Polar graph of the function r = min (sin (x), sin (sqrt (2) x), sin (sqrt (3) x), sin (sqrt (5) x)) with x = 0 to 100 π

Wolfram | Alpha query : Polar plot min (sin (x), sin (sqrt (2) x), sin (sqrt (3) x), sin (sqrt (5) x)) from x = 0 to 100 pi

Wolfram Language (Mathematica) Code :

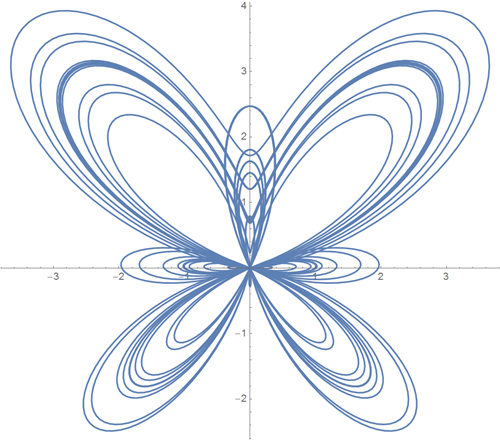
• Polar graph of the function r = exp (sin (theta)) - 2 cos (4 theta) + sin ^ 5 (theta / 12 - pi / 24)

Request to Wolfram | Alpha : Polar plot r = exp (sin (theta)) - 2 cos (4 theta) + sin ^ 5 (theta / 12 - pi / 24)

Wolfram Language (Mathematica) Code :

• Graph of a three-dimensional parametrically given surface (of a torus) {sin (s + pi / 2) + sin (s + pi / 2) sin (t + pi / 2) / 2, sin (s) + sin (s) sin (t + pi / 2) / 2, sin (t) / 2} with s = 0 to 2π and t = 0 to 2π

Wolfram | Alpha query : Parametric plot3D {sin (s + pi / 2) + sin (s + pi / 2) sin (t + pi / 2) / 2, sin (s) + sin (s) sin (t + pi / 2) / 2, sin (t) / 2} from s = 0 to 2pi and t = 0 to 2pi

Wolfram Language (Mathematica) Code :

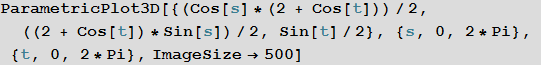
You can also use Mathematica syntax to specify many expressions and process them:

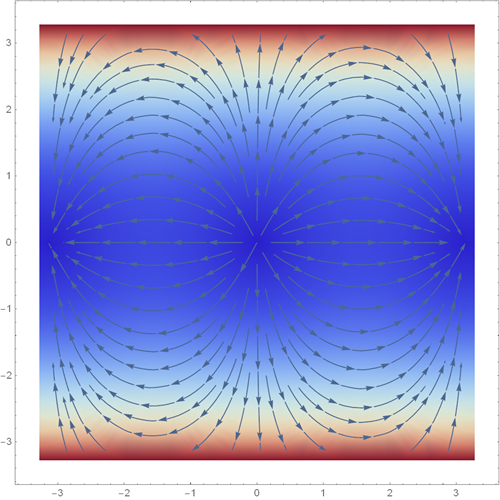
• Graph of flux density of some vector quantity {Re (sin (x + iy)), Im (Sin (x + iy))}

Wolfram | Alpha query : StreamDensityPlot [{Re [Sin [x + I y]], Im [Sin [x + I y]]}, {x, -Pi, Pi}, {y, -Pi, Pi}, ColorFunction -> “ThermometerColors”]

Wolfram Language (Mathematica) Code :

• Graph of the family of functions sin (kx) with k = 0,1,2,3, ..., 30 magenta

Wolfram | Alpha query : Plot [Table [Sin [kx], {k, 0, 30}], {x, 0, Pi / 2}] in purple

Wolfram Language (Mathematica) Code :

We can calculate some specific values of the sine function, say

• sin (π / 88)

Wolfram | Alpha : sin request (pi / 88)

Wolfram Language (Mathematica) Code :

Or, on the contrary, enter the number 0.0356923338389804557600 ... and see the result:

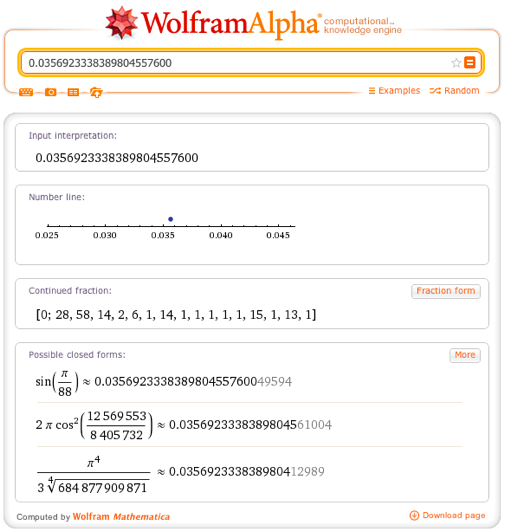
... you may notice that Wolfram | Alpha provides for this number its analytical approximation as a sine function of the argument x = π / 88 (the first of the three possible analytical forms presented above in the “Possible closed forms” section). If you are interested in this, you could ask Wolfram | Alpha to provide a list of all the “special” values of the sine function arguments and its values with these values of the argument immediately. One of the most beautiful examples of this type is the representation of the value of sin (π / 17) through radicals , which demonstrates one of the classic results that was obtained by the great mathematician Gauss on the day of his 17th birthday .

You can ask Wolfam | Alpha whether any expressions have certain properties or form:

• Is the number sin (2/3) algebraic?

Wolfram | Alpha : Is sin request (2/3) algebraic?

Wolfram Language (Mathematica) Code :

• Representation of the number sin (pi / (2 ^ 4 3 5)) through radicals

Wolfram | Alpha : Toradicals Request (sin (pi / (2 ^ 4 3 5)))

Wolfram Language (Mathematica) Code :

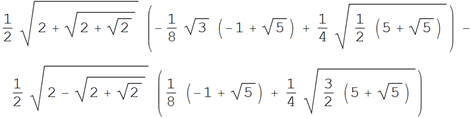
You can search for periods of various functions:

• The period of the function sin (x)

Wolfram | Alpha Request : Period of sin (x)

Wolfram Language (Mathematica) Code :

• The period of the function sin (x) + 2sin (2x) + 3sin (3x)

Wolfram | Alpha Request : Period of sin (x) + 2sin (2x) + 3sin (3x)

Wolfram Language (Mathematica) Code :

And also find the maxima and minima of the functions containing the sine function:

• Find the maximum of the function (sin (x) / x) ^ 2 located between the points π and 4π

Wolfram | Alpha : Maximize query (sin (x) / x) ^ 2 between pi and 4 pi

Wolfram Language (Mathematica) Code :

We can also build both two-dimensional and three-dimensional Lissajous figures:

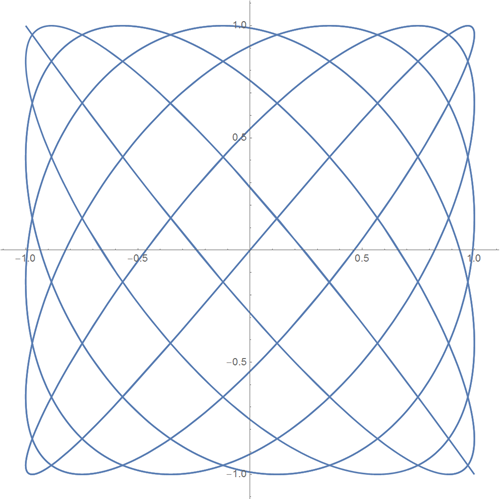
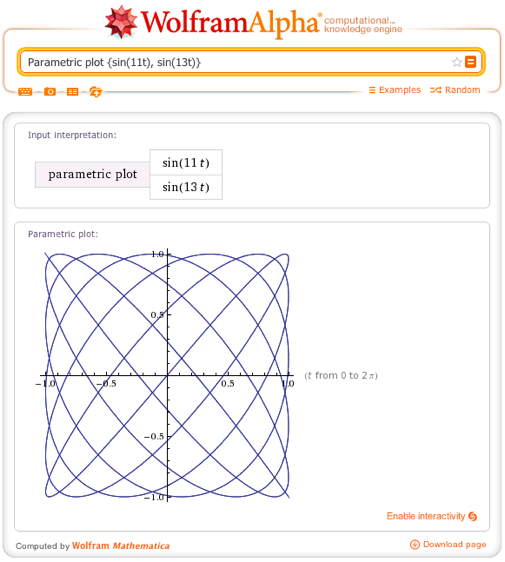
• Graph of parametrically given two-dimensional curve {sin (11t), sin (13t)}

Wolfram | Alpha Query : Parametric plot {sin (11t), sin (13t)}

Wolfram Language (Mathematica) Code :

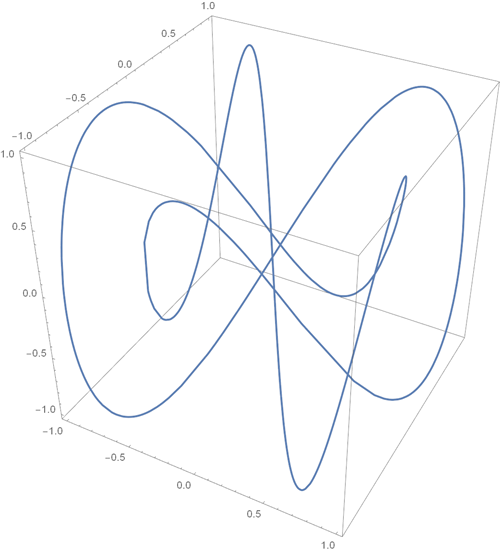
• Graph of parametrically given three-dimensional curve {sin (2t), sin (3t), sin (5t)} from t = 0 to 2pi

Wolfram | Alpha query : Parametric plot {sin (2t), sin (3t), sin (5t)} from t = 0 to 2pi

Wolfram Language (Mathematica) Code :

The result of the query is Parametric plot {sin (11t), sin (13t)} which was mentioned above:

You can not only build curves, but also calculate their curvature:

• Curvature of a parametrically given curve {sin (3t), sin (4t)} at the point t = 1

Wolfram | Alpha query : Curvature of {sin (3t), sin (4t)} at t = 1

Wolfram Language (Mathematica) Code :

Find the coordinates of the points of inflection of the curve:

• sin (x) curve inflection points

Wolfram | Alpha Request : Inflection points sin (x)

Wolfram Language (Mathematica) Code :

Or the length of the arc curve:

• Arc length of a parametrically given curve {sin (t), sin (2t)} at t = 0 to π

Wolfram | Alpha query : Arc length {sin (t), sin (2t)} from t = 0 to pi

Wolfram Language (Mathematica) Code :

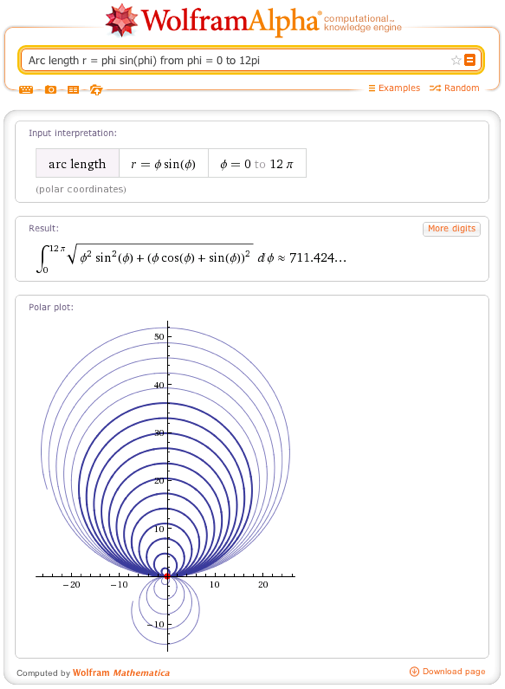
• The arc length of the polar curve is r = phi sin (phi) with phi = 0 to 12π

Wolfram | Alpha query : Arc length r = phi sin (phi) from phi = 0 to 12pi

Wolfram Language (Mathematica) Code :

Below is the result that Wolfram | Alpha gives to the previous query about the length of the curve defined in the polar coordinate system:

You can find the return point of some function:

Or check the function for frequency:

• Is sin (4x + pi / 3) periodic?

Wolfram | Alpha Request : Periodicity sin (4x + pi / 3)

Wolfram Language (Mathematica) Code :

There are many mathematical formulas that may be required. Consider a few specific examples:

• Present as a sum sin (x) ^ 10

Wolfram | Alpha Request : Trig reduce sin (x) ^ 10

Wolfram Language (Mathematica) Code :

• Present as a sum sin (10x)

Wolfram | Alpha Query : Trig expand sin (10x)

Wolfram Language (Mathematica) Code :

Similarly, you can get the basic formulas of trigonometry:

• Half-angle formula for sin (x) function

Wolfram | Alpha Request : Half-angle formulas sinx

Wolfram Language (Mathematica) Code :

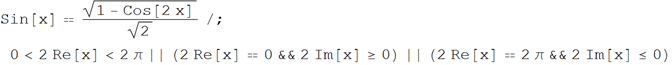
• Double angle formula for sin (x) function

Wolfram | Alpha Request : Double-angle formulas sinx

Wolfram Language (Mathematica) Code :

• Sine formulas of the sum (difference) of two or more arguments

Wolfram | Alpha Request : Addition formulas sinx

Wolfram Language (Mathematica) Code :

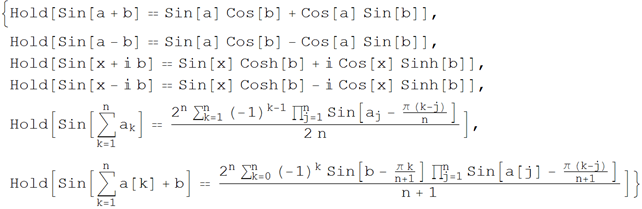
Below is the result of a query about the double angle formula for sine:

Wolfram | Alpha also knows many different representations of functions through other functional constructs:

• Representation of the sine in the form of an infinite product

Wolfram | Alpha Request : Product representations sinx

Wolfram Language (Mathematica) Code :

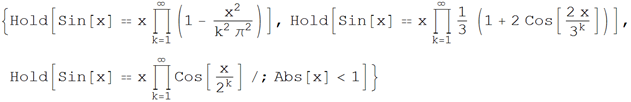
• Presentation of sine as limit

Wolfram | Alpha Request : Limit representations sinx

Wolfram Language (Mathematica) Code :

• Representation of sine through hypergeometric functions

Wolfram | Alpha : Sinx request in terms of hypergeometrics

Wolfram Language (Mathematica) Code :

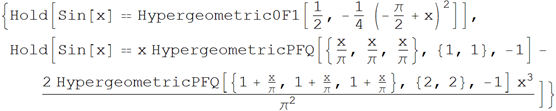
You can ask Wolfram | Alpha about the connection of the sine function with other functions:

• Representation of the function sin (x) through exponential exponential function

Wolfram | Alpha : Sinx in exponentials request

Wolfram Language (Mathematica) Code :

• Relationship between sin (x) and cos (x)

Request in Wolfram | Alpha : Relations between sin (x), cos (x)

Wolfram Language (Mathematica) Code :

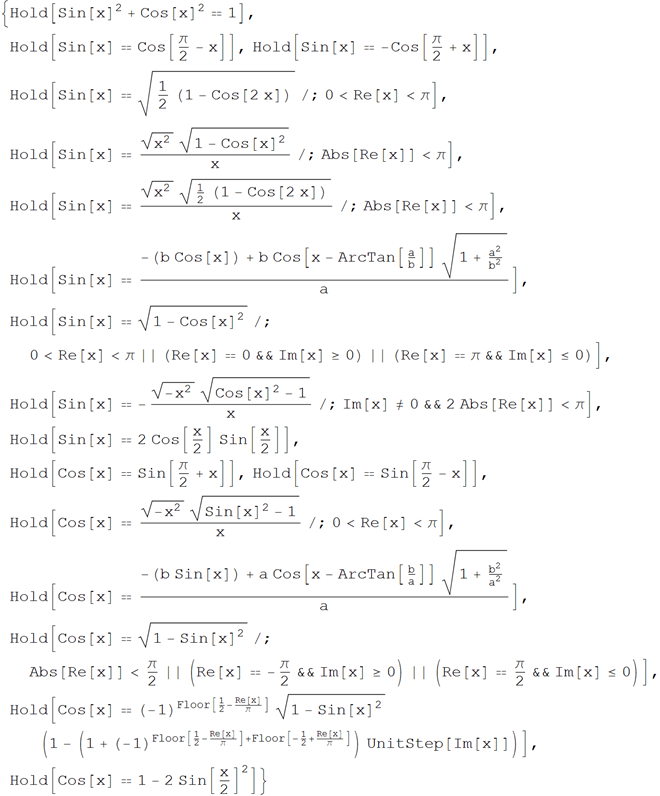
• Links between sin (x) and tg (x)

Wolfram | Alpha request : Relationship between sinx, tanx

Wolfram Language (Mathematica) Code :

You can also find a connection with the inverse function and other functions expressed through sine:

• Feedback with inverse function for sin (x)

Wolfram | Alpha query : Relations with inverse function sinx

Wolfram Language (Mathematica) Code :

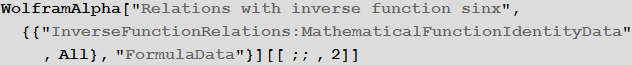
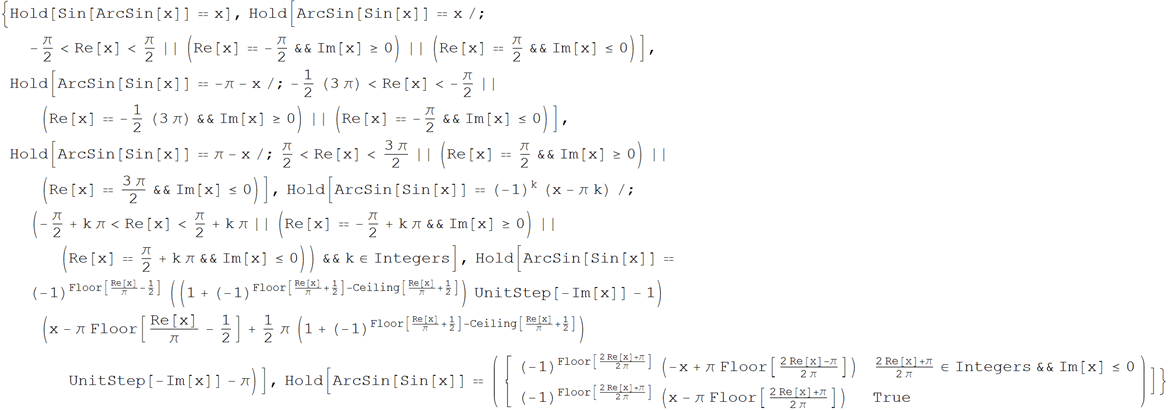
• Functions that have proper names, expressed in terms of sin (x)

Wolfram | Alpha : Named functions request through through sin (x)

Wolfram Language (Mathematica) Code :

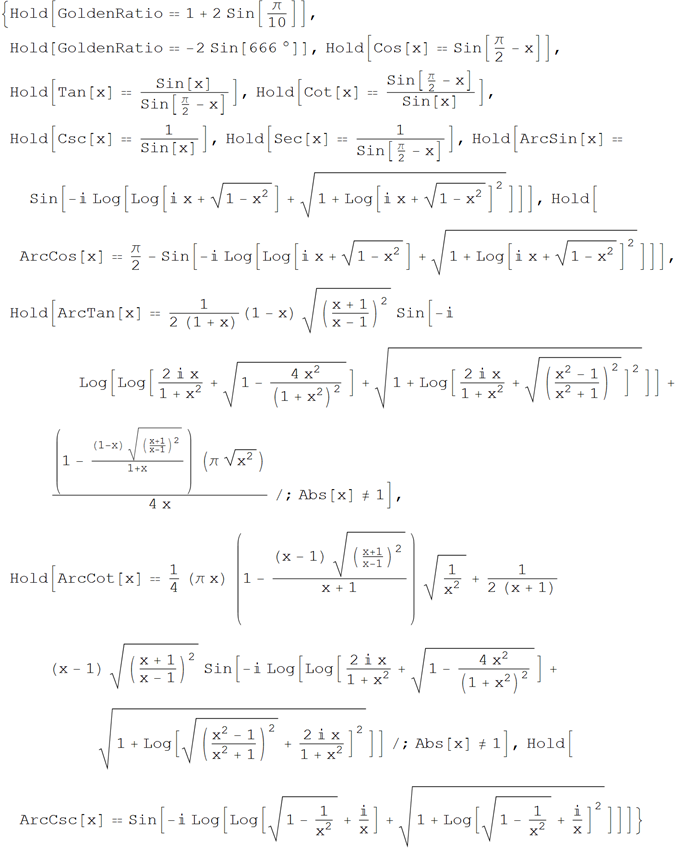
Below is the result of a previous query issued by Wolfram | Alpha:

You can solve equations and inequalities containing the sine function:

• Find all solutions of the equation cosx + sinx = tanx

Wolfram | Alpha query : Find all solutions for cosx + sinx = tanx

Wolfram Language (Mathematica) Code :

• Solve the inequality cos (x)> 2sin (x)

Wolfram | Alpha : Solve cos (x)> 2sin (x) Request

Wolfram Language (Mathematica) Code :

It is possible to prove (verify fidelity) of trigonometric identities that include the sine function:

• Check identity sin (x + y) sin (x - y) = sin ^ 2x - sin ^ 2y

Wolfram | Alpha : Verify request : sin (x + y) sin (x - y) = sin ^ 2x - sin ^ 2y

Wolfram Language (Mathematica) Code :

You can search for break points and poles of functional expressions containing a sine:

• Break points x / sin (x)

Wolfram | Alpha Request : Discontinuities x / sin (x)

Wolfram Language (Mathematica) Code :

• The poles of the function x / sin (x)

Wolfram | Alpha Request : Poles x / sin (x)

Wolfram Language (Mathematica) Code :

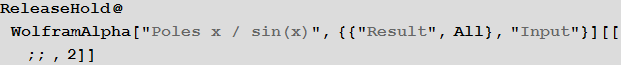
You can differentiate the sine function:

• Find the value of the sixth derivative of the function x sin (2 ^ x) with x = 0

Wolfram | Alpha query : Sixth derivative of x sin (2 ^ x) at x = 0

Wolfram Language (Mathematica) Code :

• Find the n-th derivative of the function sin (x)

Wolfram | Alpha : d ^ n / dx ^ n sin (x) query

Wolfram Language (Mathematica) Code :

You can find the final amount:

• Find the sum of sin (kx) with k = 1 to n

Wolfram | Alpha query : Sum sin (kx) for k = 1 to n

Wolfram Language (Mathematica) Code :

And, of course, it is also easy to find various integrals containing a sine:

• Find the integral of the function sin (x) over the variable x ranging from 0 to π

Wolfram | Alpha query : Integrate sin (x) dx from x = 0 to pi

Wolfram Language (Mathematica) Code :

• Find the indefinite integral of the function sin (x ^ 3) ^ 3 over x

Wolfram | Alpha query : Integrate sin (x ^ 3) ^ 3 dx

Wolfram Language (Mathematica) Code :

• Apply the integration formula in parts to an integral with the integrand function cos ^ 2 (x) sin ^ 4 (x)

Wolfram | Alpha Request : Integrate by parts cos ^ 2 (x) sin ^ 4 (x)

Wolfram Language (Mathematica) Code :

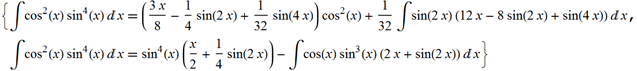
• The mean square value of the sin function (4x + pi / 3)

Wolfram | Alpha Request : Root mean square sin (4x + pi / 3)

Wolfram Language (Mathematica) Code :

Below is the result of the integration request in parts (see above) issued by Wolfram | Alpha:

You can get lists of formulas based on integrals, sums, series and products that would contain the sine function:

• Final amounts containing sine

Wolfram | Alpha Query : Finite sums containing sin (x)

Wolfram Language (Mathematica) Code :

• Infinite amounts containing sine

Wolfram | Alpha query : Infinite sums containing sinx

Wolfram Language (Mathematica) Code :

• Works containing sine

Wolfram | Alpha Request : Products containing sinx

Wolfram Language (Mathematica) Code :

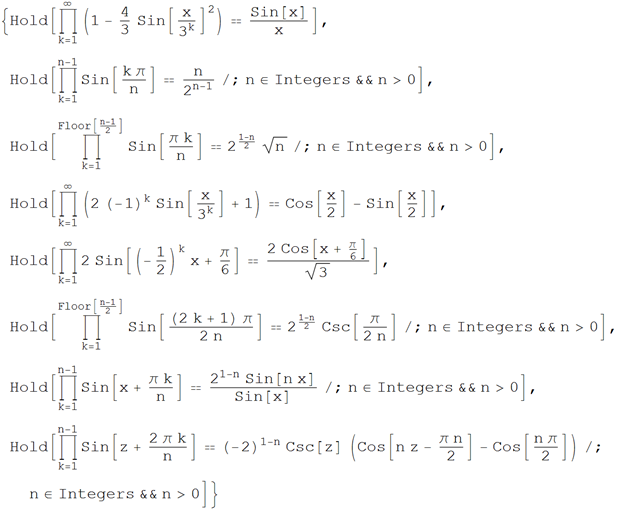
• Indefinite integrals containing sine

Wolfram | Alpha Request : Indefinite integrals containing sinx

Wolfram Language (Mathematica) Code :

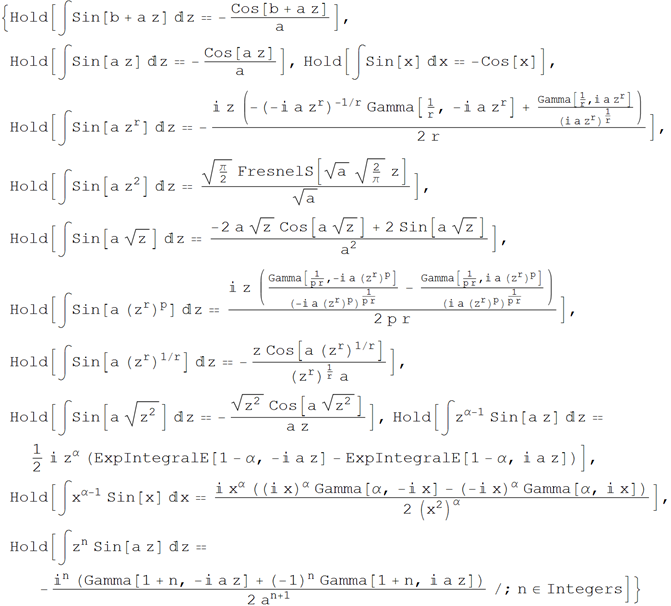
• Certain integrals containing sine

Wolfram | Alpha Request : Definite integrals containing sinx

Wolfram Language (Mathematica) Code :

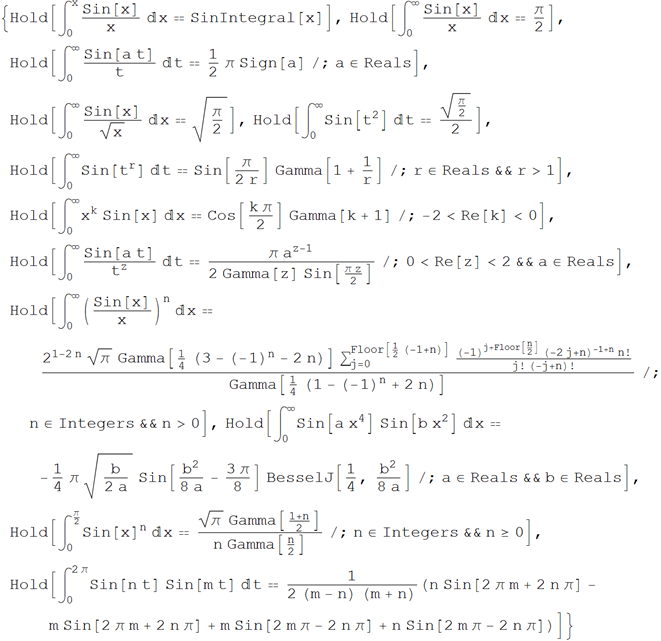
You can find various integral transforms of the sine function:

• Fourier transform of the sin (x) function

Wolfram | Alpha : Fourier transform of sin (x) query

Wolfram Language (Mathematica) Code :

• The Laplace transform of the sin (x) function

Wolfram | Alpha Query : Laplace transform of sin (x)

Wolfram Language (Mathematica) Code :

• Hilbert transform function of of sin (x)

Wolfram | Alpha : Hilbert transform of sin (x) query

Wolfram Language (Mathematica) Code :

You can also calculate various limits:

• Limit as x approaches the 0 function ln (2 + sqrt (arctan (x) * sin (1 / x)))

Wolfram | Alpha query : Limit as x goes to 0 of ln (2 + sqrt (arctan (x) * sin (1 / x)))

Wolfram Language (Mathematica) Code :

• sin (x) / x limit with x -> 0

Wolfram | Alpha Request : Lim sin (x) / x as x -> 0

Wolfram Language (Mathematica) Code :

Below is the result of a request to search for the previous limit that Wolfram | Alpha issues:

You can get the decomposition of the sine function in a row:

• Find the decomposition of the function sin (x) to the tenth order of smallness in a neighborhood of the point x = 0

Wolfram | Alpha Request : Series of sin (x) to order 10

Wolfram Language (Mathematica) Code :

Find the sum of the Taylor series of infinite order in analytical form:

• Sum the partial sums of the Taylor series of the sin (x) function

Wolfram | Alpha Query : Summed truncated Taylor series of sin (x)

Wolfram Language (Mathematica) Code :

Or get a Pade approximation of the sine function:

• [5/5] Pade approximation of sin (x) function

Wolfram | Alpha Request : [5/5] pade of sin (x)

Wolfram Language (Mathematica) Code :

Or you can simplify complex expressions that contain a sine:

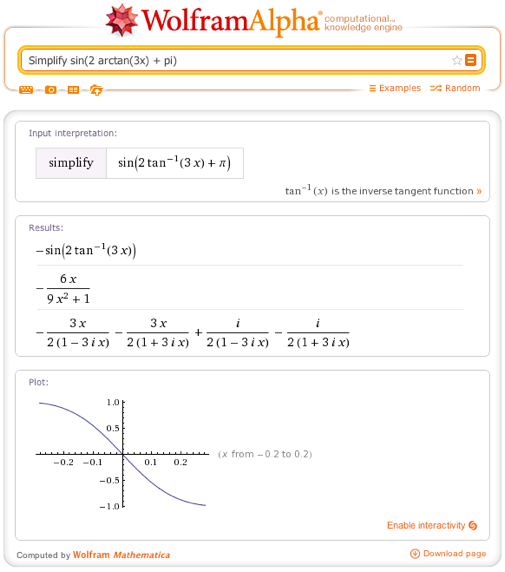
• Simplify sin (2 arctan (3x) + pi)

Wolfram | Alpha Query : Simplify sin (2 arctan (3x) + pi)

Wolfram Language (Mathematica) Code :

Below is the result of a request to simplify the trigonometric expression, discussed above, which gives Wolfram | Alpha:

It is also easy to find the decomposition of a function in a Fourier series in sines:

• Expansion of the function unitstep (x) in a Fourier series in sine

Wolfram | Alpha Request : Fourier sin series unitstep (x)

Wolfram Language (Mathematica) Code :

The sine function has many related functions and generalizations that include, but are not limited to, say the following:

• haversin (x)

Wolfram | Alpha Request : haversin (x)

Wolfram Language (Mathematica) Code :

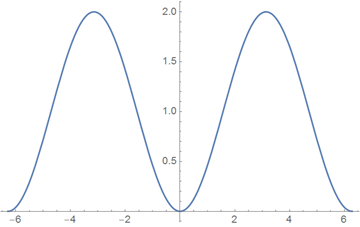
• versin (x)

Wolfram | Alpha query : versin (x)

Wolfram Language (Mathematica) Code :

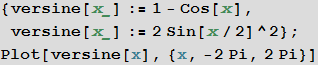
• qsin (x)

Wolfram | Alpha query : qsin (x)

Wolfram Language (Mathematica) Code :

You can use the sine function in probability theory, for example, you can find the expectation of a random variable sin (x) if the random variable x is normally distributed with a expectation of 0 and a variance of 1:

• Mathematical expectation sin (x) if x has a standard normal distribution

Wolfram | Alpha : E (sin (x)) query where x ~ N (0.1)

Wolfram Language (Mathematica) Code :

Below is the result of a query about the value of the mathematical expectation of the expression sin (x), discussed above, which gives Wolfram | Alpha:

We can find solutions to differential equations containing sine:

• y '+ sinx y = 0

Request Wolfram | Alpha : y '+ sinx y = 0

Wolfram Language (Mathematica) Code :

• y “- 1/3 y '+ sin xy ^ 3 = 0

Request in Wolfram | Alpha : y ”- 1/3 y '+ sin xy ^ 3 = 0

Wolfram Language (Mathematica) Code :

• cos (x) dx + sin (y) dy = 0

Wolfram | Alpha query : cos (x) dx + sin (y) dy = 0

Wolfram Language (Mathematica) Code :

You can calculate the Vronskian system of functions, which contains the sine:

• Wronskian system of functions {cos (x), sin (x)}

Request Wolfram | Alpha : Wronskian ({cos (x), sin (x)}, x)

Wolfram Language (Mathematica) Code :

And you can also find a differential equation whose solution is a given function depending on the sine:

• Find the differential equation for the function sin (x ^ p)

Wolfram | Alpha : Differential equation for sin (x ^ p) query

Wolfram Language (Mathematica) Code :

You can work with the sine theorem or its spherical analogue:

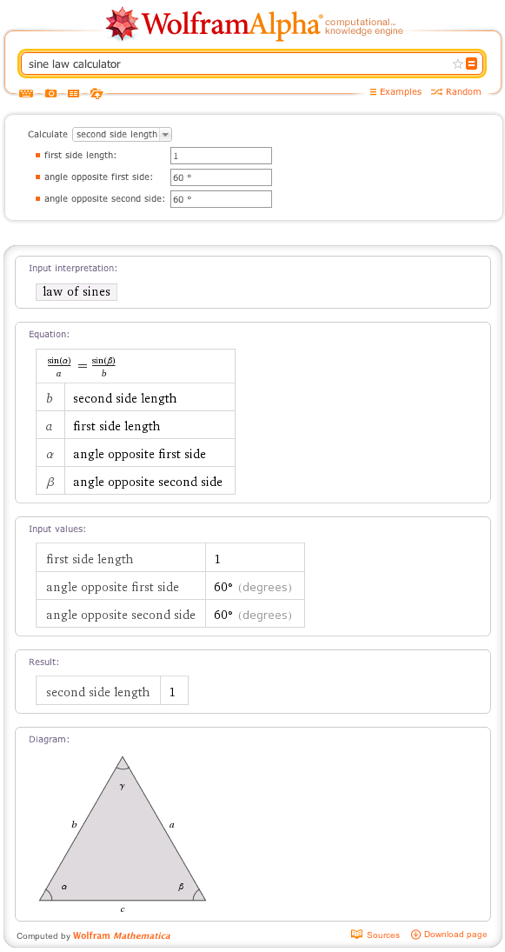
• Sine Theorem Calculator

Wolfram | Alpha Request : sine law calculator

Wolfram Language (Mathematica) Code :

• Sinus theorem in spherical geometry

Wolfram | Alpha Request : spherical law of sines

Wolfram Language (Mathematica) Code :

Below is the result of the query calculator of the sine theorem, discussed above, which gives Wolfram | Alpha:

You can express and approximate the value of the number π through the values of the sine function:

• Express 3.14 in sin (1) and sin (2)

Wolfram | Alpha Request : Express 3.14 through sin (1) and sin (2)

Wolfram Language (Mathematica) Code :

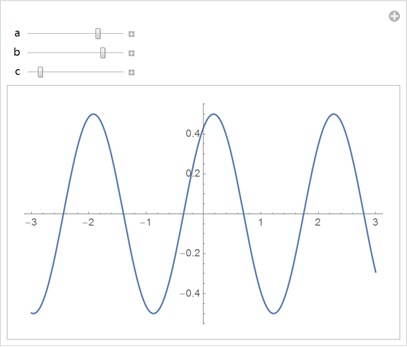
And also get an interactive model of the sine function:

• Vary the parameters a, b, c in the expression Plot [a Sin [bx + c], {x, -3, 3}]

Wolfram | Alpha query : Vary Plot [a Sin [bx + c], {x, -3, 3}]

Wolfram Language (Mathematica) Code :

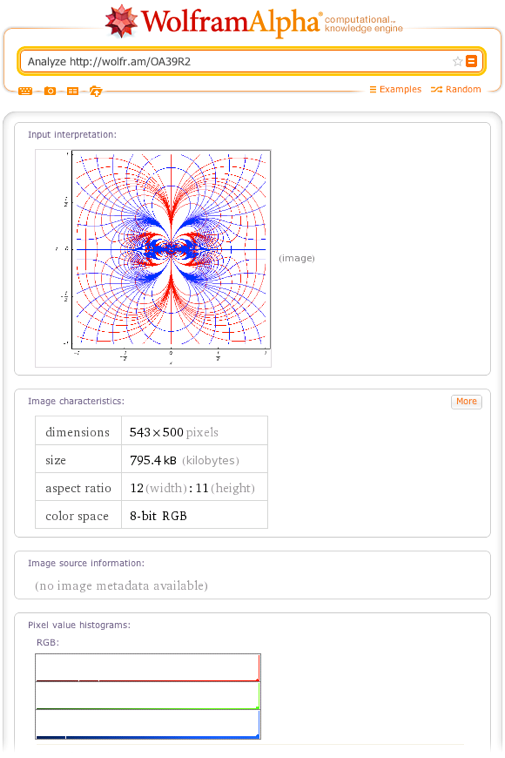
You can also perform calculations on objects that are on the Internet, if you just have a link to them, for example, we perform an image analysis of the sine function, which is taken from The Wolfram Functions Site website about the Wolfram Research functions:

• Perform analysis of wolfr.am/OA39R2

Wolfram | Alpha query : Analyze wolfr.am/OA39R2

Below is the result of a previous query that Wolfram | Alpha issues:

Finally, you can "play" the sine function:

• Play sin (440 t)

Wolfram | Alpha : Play sin request (440 t)

Wolfram Language (Mathematica) Code :

Of course, we can continue further (and further and further), but there are surely enough written examples (there are actually a lot of them).

Source: https://habr.com/ru/post/255021/

All Articles

Top 100+ Wolfram | Alpha Sine Functions, or Wolfram | Alpha Overview of Mathematical Features and Syntax

More articles: