In the previous article , we smashed all the available segments by intersection points, thus ensuring that we no longer have intersecting segments. In this part, we will join the obtained segments into contours and define their fill.

Contour search

So, we have a set of non-intersecting segments. Let's look for contours that will be useful to us to identify polygons. In the figure on the right we see 6 red lines and 3 blue ones. It would be nice to find the contours of ABFDC, DFE and FGD. Composite contours (for example, ABFGDC) do not interest us, which means either our algorithm should not stumble upon them in principle, or else we will have to exclude these contours later.

Search by search

The first algorithm that came to my mind initially showed itself well. Here is what it looks like:

1. For simplicity, we double the number of segments, adding for each segment its backward-directed clone (this will allow us to walk along the segments as along vectors, without having to walk along the “back” segments).
2. Consistently take each segment for the initial for the desired contour, put it in a new array and call the recursive search procedure (below).
3. We look through all the segments looking for one that fits in with the beginning of the last one found and its end point has not yet met among the segment points in the array, and add it to the end of the array.
4. If the end of this segment coincides with the beginning of the first segment of the array, then we have found the contour - add an array of segments to the array of contours found and exit the recursion.
5. If not, recursively call the procedure for finding the next segment.

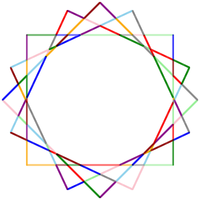Adding to this algorithm the procedure for elimination of composite contours, you can get something quite workable. And I thought everything was fine until I was confronted with a real situation (see pictures). Pay attention to the yellow "star" on the chain of a famous character. It is drawn by imposing a set of squares turned around its center. After splitting the segments at the intersection points, the first we have is 112 pieces. I did not manage to wait until the end of the search for contours on this image. But indeed, the estimate of the time of such sorting over the number of segments is O (n!), Which, as you understand, is normal for a dozen segments, but completely unacceptable for a hundred. I had to think about another algorithm.

Directed search by the choice of the "extreme" segment

Let's go back to the original picture (it is duplicated on the left). If we, in search of the next segment for the future contour, came along the vector from point B to point F, then it makes sense to move on either to point D or to point G, since Moving along the FE vector, we will obviously choose a segment belonging to the composite contour! Those. as a minimum, we can already greatly reduce the search (from each point we can go a maximum of two ways). And that's good, but let's think further. Note that the above iteration algorithm finds all contours two times (once - moving clockwise, and another time - when it goes in sections counterclockwise). What if in each branch we choose only the most extreme segment in the sense of moving clockwise? (In the example: if the last segment vector was BF, then the next one will be FD.) We will find all the necessary contours! Without recursion! Miracles!
')
It is worth mentioning here that although we go clockwise, sometimes we will find contours with a left circuit (counterclockwise), if the starting vector segment does not belong to any circuit with a right circuit. Moreover, these left contours can be composite (In the figure: vector AB belongs to the right contour of ABFDC, and here vector BA is the composite left contour of BACDGF.) So, we will need to exclude all left contours from the resulting array.

Here's how to determine whether the contour is right (here (x1, y2) is the starting point of the segment, (x3, y3) is the final one):

function isClockwise() { var sum = 0.0; for (edge in edges) { sum += (edge.x3 - edge.x1) * (edge.y3 + edge.y1); } return sum >= 0; } 

The resulting algorithm is already working at an acceptable speed (of the order of O (n ^ 2), as far as I understand it; correct it if I am mistaken) and it shows itself perfectly on real problems. And we go further.

Detection of polygons by contours found

So, we have contours. It is time to put them into polygons (remember that a polygon is an external contour + a set of internal contours- “holes”). The task is well solved "in the forehead":

1. We take successively each contour for the external contour of the future polygon.
2. Among the remaining contours we look for those that lie inside our external contour.
3. Take a point lying inside the outer contour, but outside its “holes”.
4. On the original image, we take the fill at this point (ie, we are looking for the polygon to which it belongs), and if such a polygon is located, we add the outer contour + “holes” as a new polygon to the array found for the original image.
5. Similarly, for the final image (look for the polygon to which the point belongs and if it is, add a new polygon to the array found for the final image).

Thus, we “reconstruct” the original and final image after intersecting all the segments. And now we are guaranteed to have that each of the polygons of the original image either coincides (in the sense of coordinates) with the same polygon of the overlaid image, or stands out for the limits of all its polygons.

I think you should pay special attention to paragraph 3. How to take a good point inside the contour outside of its internal contours? To begin with, we need to understand that the point then lies inside the polygon, when the beam emitted from it in any direction intersects with the polygon segments an odd number of times. And everything is good, except that due to the limited accuracy of calculations, the beam can get to the junction of the segments, which can cause incidents (detection of intersections with both segments, either with one or with one at all). Most often, to simplify calculations, the beam is released horizontally. We will also do so. Here is what we now know about a good point:

• it should not coincide with any of the ends of the segments that make up the polygon (and the more does not coincide - the better);
• It is desirable that the point lies far away from the segments of the polygon in order to reduce the likelihood of problems associated with the detection of intersections of a beam emitted from it with these segments.

The following algorithm of searching for the y coordinate for such a point comes to mind:

1. We drive into the array all the y coordinates of the ends of the segments that make up the polygon.
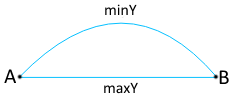2. We add to it minY and maxY of our external contour (since these values ​​do not always coincide with the values ​​at the ends of the segments - see fig. On the right).
3. Sort the array in ascending order.
4. We are looking for a sequential pair of values ​​(y1, y2) in the array for which the difference y2 - y1 is maximal.
5. We take the arithmetic average of these values ​​for the y coordinate of the desired point: y = (y1 + y2) / 2 .

It remains to find a convenient x value for us. For this:

1. Release the horizontal beam from the point (infinity; y) to the right.
2. Find all the coordinates x of the point of intersection of the ray with the segments of the polygon;
3. Sort them ascending.
4. We choose among pairs (x [i], x [i + 1]) , where i = 0,2,4 ... such, for which the difference x [i + 1] - x [i] is maximal.
5. We take the arithmetic average of this pair for the value of the x coordinate of the desired point: x = (x [i] + x [i + 1]) / 2 .

The resulting algorithm is not perfect, but simple enough and, as practice shows, works well on real-world problems.

Last steps

Within the article, we will not consider in detail the remaining points of the image combining search algorithm:

• removal of all edges of the original image, which are completely inside the shaded areas of the overlay image;
• removal from the original image of all polygons present in the overlay image without taking into account the color;
• adding to the edges and polygons of the original image of all edges and polygons of the overlay image (in this case, the coinciding edges of the original image are rubbed with the edges of the overlay);
• the union on the original image of adjacent polygons that have the same fill and do not have a clear separation of the edges.

I believe that these subtasks are quite trivial and readers can easily (if necessary) deal with this on their own.

Conclusion

In the article I tried to show a number of interesting moments related to the search for the union of vector images. Some features remained behind the scenes, because they are either too small, or the author just forgot about them. I will be glad to any clarifications both on the article and on the described algorithms.