Quite simple about minimal perfect graph-based hashing
Imagine that we are faced with the classic task of obtaining data by some key. Moreover, the amount of data and their keys is known in advance.
How to solve a similar problem?
If the number of key-value pairs is obviously small, then it makes sense to simply be hard-coded. But if such values are many millions?
')
You can simply go through the list until the desired key value is found. But then the complexity will be linear O (N) , which, in this case, should upset any engineer. And what is the complexity of the algorithm then required? Which does not depend on the amount of data and runs in a fixed time, i.e. with constant complexity O (1) .
How can I get data for a fixed time?
If you arrange the data in memory sequentially, then knowing the offset where the necessary information is located, you can get access that will not depend on the initial amount of data.
In other words, we need to find a way to convert the key to the offset where the data will be. The offset is just an integer: [0, n - 1], where n is the number of stored values.
Hash functions come to the rescue, the task of which is just to convert keys to integers. Such numbers can be interpreted as offsets, which store data.
But, unfortunately, hash functions generate collisions, that is, two different keys can give the same offset.
Based on the task, we have a fixed and previously known amount of data, which makes it possible to avoid such problems.
An ideal hash function (Perfect Hash Function) is such a hash function that converts a previously known static set of keys into a range of integers [0, m - 1] without collisions, that is, one key corresponds to only one unique value. And if the number of resulting values is the same as the number of incoming keys, this function is called the Minimal Perfect Hash Function.
Let's fantasize and imagine that each key corresponds to one unique edge, and, accordingly, two vertices.
Then the key can be represented as such a primitive graph:

Figure 1. The graph where the edge corresponds to the key and is described through two vertices.
Since the key is represented as an edge, and the edge always connects at least (because there are still hypergraphs) two vertices, the desired function may look like this:
h (key) = g (node1, node2)
where h (key) is the minimal ideal hash function, the value of which describes the edge, key is the key, g () is some unknown function depending on the nodes of the graph node1 and node2 . Since they should depend on the key, it turns out
h (key) = g (f1 (key), f2 (key))
In fact, for f1 and f2, you can choose any hash functions that will be used for one key.
It remains to determine the unknown function g () , which describes the interrelation of two nodes f1 (key), f2 (key) and edge.
For simplicity, we define the value of the edge as the sum of the values of the nodes connected by this edge.
Since the edge corresponds to only one key, this is the desired value, the result of the minimal ideal function.
h (key) = (g1 (f1 (key)) + g2 (f2 (key))) mod m
where h (key) is the value of the edge, f1 (key) is the first node of the graph, g1 () is the value of this node, f2 (key) is the second node, g2 () is the value of the second node, m is the number of edges.
If it is even easier, then
the value of the minimal ideal function = (node value 1 + node value 2) mod number of edges.
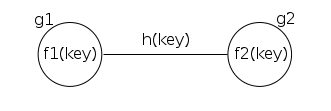
Figure 2. Representation of a single key in the graph.
In other words, hash functions are used to determine node numbers, and collisions often occur, so a single node can contain multiple edges.
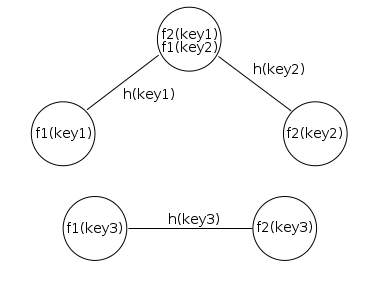
Figure 3. Collisions in hash functions generate several edges on the same vertex. Also, the vertices of one key may not connect to the vertices of another key.
Having defined how the nodes of the graph are interconnected with their edges, we first determine the values of the edges h (key) (this is just an incremental index), which will be obviously unique, and then select the values of the nodes.
For example, the value of the subsequent node can be calculated as:
g2 (f2 (key)) = h (key) - g1 (f1 (key))
or
node value 2 = edge value - node 1 values
It remains only to go through the graph, take 0 for the initial value of the first node of the subgraph and count all the others.
Unfortunately, this approach does not work if the graph is looped. Since there is no way to guarantee in advance that the graph will not be clogged, in case of obsession it will be necessary to redraw the graph with other hash functions.
It is best to check looping by removing vertices with only one edge. If the vertices remain, then the graph is looped.
Now it's time to describe the algorithm itself with an example.
Task: There are many keys consisting of 12 month names. It is necessary to create a minimal ideal hash function, where each month is transmitted to only one unique integer in the range [0, 11].
1. Pass through all the keys and add vertices and edges. To do this, select the two hash functions f1 and f2 .
For example:
For the jan key, we get the number of the first node f1 (jan) : = 4 and the number of the second node f 2 (jan) : = 13
For the key feb , f1 (feb) : = 0, f 2 (feb) : = 17
and so on.
2. Check if the graph is looped, if yes, then repeat step # 1 again and at the same time change the hash of the function f1 / f2 .
The probability of a cycle appearing in a graph depends on the number of possible vertices. Therefore, we introduce the concept as a factor of the graph size. The number of nodes is defined as:
m = c * n
where m is the number of nodes in the graph, c is the constant size factor, n is the number of keys.
3. In case of successful creation of a non-cycled graph, you must go through all the nodes and calculate their value using the formula
g2 (f2 (key)) = h (key) - g1 (f1 (key))
or
child node value = edge index - ancestor node value
For example, assign the node 0 with the value 0 and go along its edge with the index 6:
g2 (13) = 6 - 0 = 6, the node with the number 13 gets the value 6, and so on.
As a result, we have such a graph.
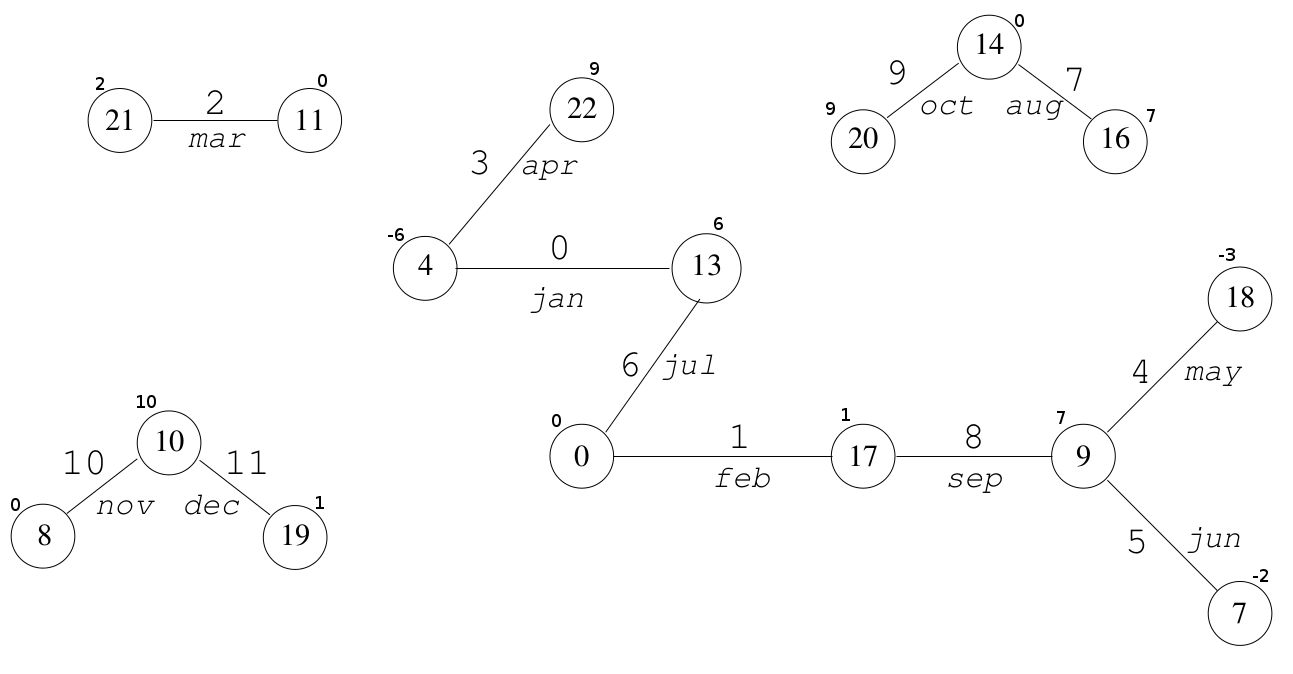
Figure 4. The resulting graph, where the keys are the names of the months and used random hash functions to obtain the numbers of the vertices. The numbers near the nodes are the value of the node.
Suppose we need to get a unique index on the key sep .
We use the same hash functions that were used to create the graph:
f1 (sep): = 17
f2 (sep): = 9
After getting the vertex numbers, we add their values:
h (sep) = (g (17) + g (9)) mod 12 = (1 + 7) mod 12 = 8
This algorithm is called CHM and is implemented in the CMPH library.
And as you can see, the creation of the hash table has linear complexity O (N) , and the index search by key is constant O (1) .
Do you remember the bearded puzzle from Google?
How to copy a unidirectional list in linear time, if the list node looks like this?
And the solution was supposed to clone the nodes so that two copies of the node were in a row, and then divide this list with copies of the nodes into two lists, each with a copy. As a result, the complexity is linear.
And now imagine at your disposal the minimal ideal hash function that can save its index in the list by pointer and save the pointer by index. And you can solve the problem like this:
1. Pass the list, we get an array of pointers of nodes and their index.
2. Create minimal ideal hash functions for node pointers.
3. Create a new list, get an array of indexes of nodes and their pointers.
4. We create other ideal functions for the indices of the second list, so that we can get an address by the index.
5. We pass the new list, and we get the address of the old node, we get the index by it, and by the second hash function we get the address in the second list by index.
As a result, the list will be copied in linear time.
Although, of course, the idea is to duplicate the nodes and then divide them into two lists, more beautiful and faster.
Thanks for the effort.
1. ZJ Czech, G. Havas, and BS Majewski. Information Processing Letters, 43 (5): 257-264, 1992.
2. Minimal Perfect Hash Functions - Introduction .
3. mphf - My implementation of CHM in C ++.
How to solve a similar problem?
If the number of key-value pairs is obviously small, then it makes sense to simply be hard-coded. But if such values are many millions?
')
You can simply go through the list until the desired key value is found. But then the complexity will be linear O (N) , which, in this case, should upset any engineer. And what is the complexity of the algorithm then required? Which does not depend on the amount of data and runs in a fixed time, i.e. with constant complexity O (1) .
How can I get data for a fixed time?
Hashing
If you arrange the data in memory sequentially, then knowing the offset where the necessary information is located, you can get access that will not depend on the initial amount of data.
In other words, we need to find a way to convert the key to the offset where the data will be. The offset is just an integer: [0, n - 1], where n is the number of stored values.
Hash functions come to the rescue, the task of which is just to convert keys to integers. Such numbers can be interpreted as offsets, which store data.
But, unfortunately, hash functions generate collisions, that is, two different keys can give the same offset.
Based on the task, we have a fixed and previously known amount of data, which makes it possible to avoid such problems.
Perfect hashing
An ideal hash function (Perfect Hash Function) is such a hash function that converts a previously known static set of keys into a range of integers [0, m - 1] without collisions, that is, one key corresponds to only one unique value. And if the number of resulting values is the same as the number of incoming keys, this function is called the Minimal Perfect Hash Function.
Consider an example of a minimal ideal hash function based on random graphs.
Let's fantasize and imagine that each key corresponds to one unique edge, and, accordingly, two vertices.
Then the key can be represented as such a primitive graph:

Figure 1. The graph where the edge corresponds to the key and is described through two vertices.
Since the key is represented as an edge, and the edge always connects at least (because there are still hypergraphs) two vertices, the desired function may look like this:
h (key) = g (node1, node2)
where h (key) is the minimal ideal hash function, the value of which describes the edge, key is the key, g () is some unknown function depending on the nodes of the graph node1 and node2 . Since they should depend on the key, it turns out
h (key) = g (f1 (key), f2 (key))
In fact, for f1 and f2, you can choose any hash functions that will be used for one key.
It remains to determine the unknown function g () , which describes the interrelation of two nodes f1 (key), f2 (key) and edge.
This is where tricks begin.
For simplicity, we define the value of the edge as the sum of the values of the nodes connected by this edge.
Since the edge corresponds to only one key, this is the desired value, the result of the minimal ideal function.
h (key) = (g1 (f1 (key)) + g2 (f2 (key))) mod m
where h (key) is the value of the edge, f1 (key) is the first node of the graph, g1 () is the value of this node, f2 (key) is the second node, g2 () is the value of the second node, m is the number of edges.
If it is even easier, then
the value of the minimal ideal function = (node value 1 + node value 2) mod number of edges.

Figure 2. Representation of a single key in the graph.
In other words, hash functions are used to determine node numbers, and collisions often occur, so a single node can contain multiple edges.

Figure 3. Collisions in hash functions generate several edges on the same vertex. Also, the vertices of one key may not connect to the vertices of another key.
That's where the salt is
Having defined how the nodes of the graph are interconnected with their edges, we first determine the values of the edges h (key) (this is just an incremental index), which will be obviously unique, and then select the values of the nodes.
For example, the value of the subsequent node can be calculated as:
g2 (f2 (key)) = h (key) - g1 (f1 (key))
or
node value 2 = edge value - node 1 values
It remains only to go through the graph, take 0 for the initial value of the first node of the subgraph and count all the others.
Unfortunately, this approach does not work if the graph is looped. Since there is no way to guarantee in advance that the graph will not be clogged, in case of obsession it will be necessary to redraw the graph with other hash functions.
It is best to check looping by removing vertices with only one edge. If the vertices remain, then the graph is looped.
On a simple example
Now it's time to describe the algorithm itself with an example.
Task: There are many keys consisting of 12 month names. It is necessary to create a minimal ideal hash function, where each month is transmitted to only one unique integer in the range [0, 11].
1. Pass through all the keys and add vertices and edges. To do this, select the two hash functions f1 and f2 .
For example:
For the jan key, we get the number of the first node f1 (jan) : = 4 and the number of the second node f 2 (jan) : = 13
For the key feb , f1 (feb) : = 0, f 2 (feb) : = 17
and so on.
2. Check if the graph is looped, if yes, then repeat step # 1 again and at the same time change the hash of the function f1 / f2 .
The probability of a cycle appearing in a graph depends on the number of possible vertices. Therefore, we introduce the concept as a factor of the graph size. The number of nodes is defined as:
m = c * n
where m is the number of nodes in the graph, c is the constant size factor, n is the number of keys.
3. In case of successful creation of a non-cycled graph, you must go through all the nodes and calculate their value using the formula
g2 (f2 (key)) = h (key) - g1 (f1 (key))
or
child node value = edge index - ancestor node value
For example, assign the node 0 with the value 0 and go along its edge with the index 6:
g2 (13) = 6 - 0 = 6, the node with the number 13 gets the value 6, and so on.
As a result, we have such a graph.

Figure 4. The resulting graph, where the keys are the names of the months and used random hash functions to obtain the numbers of the vertices. The numbers near the nodes are the value of the node.
Lukup
Suppose we need to get a unique index on the key sep .
We use the same hash functions that were used to create the graph:
f1 (sep): = 17
f2 (sep): = 9
After getting the vertex numbers, we add their values:
h (sep) = (g (17) + g (9)) mod 12 = (1 + 7) mod 12 = 8
This algorithm is called CHM and is implemented in the CMPH library.
And as you can see, the creation of the hash table has linear complexity O (N) , and the index search by key is constant O (1) .
Afterword
Do you remember the bearded puzzle from Google?
How to copy a unidirectional list in linear time, if the list node looks like this?
struct list_node
{
list_node * next;
list_node * random;
};
And the solution was supposed to clone the nodes so that two copies of the node were in a row, and then divide this list with copies of the nodes into two lists, each with a copy. As a result, the complexity is linear.
And now imagine at your disposal the minimal ideal hash function that can save its index in the list by pointer and save the pointer by index. And you can solve the problem like this:
1. Pass the list, we get an array of pointers of nodes and their index.
2. Create minimal ideal hash functions for node pointers.
3. Create a new list, get an array of indexes of nodes and their pointers.
4. We create other ideal functions for the indices of the second list, so that we can get an address by the index.
5. We pass the new list, and we get the address of the old node, we get the index by it, and by the second hash function we get the address in the second list by index.
As a result, the list will be copied in linear time.
Although, of course, the idea is to duplicate the nodes and then divide them into two lists, more beautiful and faster.
Thanks for the effort.
Read
1. ZJ Czech, G. Havas, and BS Majewski. Information Processing Letters, 43 (5): 257-264, 1992.
2. Minimal Perfect Hash Functions - Introduction .
3. mphf - My implementation of CHM in C ++.
Source: https://habr.com/ru/post/254431/
All Articles