Algorithm Tasks
Good day. In the first year of undergraduate studies at the Academic University, an annual course of algorithms is read. Each lecture is accompanied by a seminar at which we parse algorithmic problems. Practical seminars are held in small groups. This semester, I lecture and practice in one of the groups.
Today I want to share with you two tasks from these seminars.
Problem 1. On the line are given n segments, you need to choose the maximum size of the subset of non-intersecting.
')
Task 2. On the circle there are n arcs (segments), you need to choose the maximum size of the subset of non-intersecting.
The first task is one of the examples on the topic of “greedy algorithms”. The solution can be viewed below. In short, the solution is supposed to be sorted by O (sort + n). Here, for sort, I denote the time to sort an array of length n. By the way, sort is optional nlogn (for example, bucket sort, radix sort, input data from a limited range).
The second problem has a beautiful probabilistic solution for O (sort + n). Despite its similarity to the first, the second task is not solved by greed in the forehead. Rather, I personally do not know the greedy decision, if someone from the readers comes up with and shares, I will be glad to listen. And in order to make it easier to think, I will immediately describe several non-working ideas that most often come up when trying to solve this problem:
Problem solving 1.
Each segment i has a left end L [i] and a right end R [i]. We sort the segments in ascending order R [i]. In this order, we will go through the segments. The next segment will be added to the response if its left border is greater than the maximum of the right borders of already added segments.
Problem solving 2.
I warn you, the solution is long and much more complicated than the previous one. On the other hand, there are no fundamentally complex ideas here, so everything can be understood without initial preparation.
For a start, let's say how arcs are defined on a circle. Let the circle be the looped segment [0..M), and the arcs (segments) of the circle are given by the pairs L [i] .. R [i]. If R [i] <L [i], the segment passes through the point M.
The main idea of the solution is to find a point where a circle can be cut. Or rather, choose the segment i, which we will definitely take in response. As soon as such segment i is fixed, the circle can be cut, for example at the point R [i].
Representing all objects on a circle, solving a problem is not very convenient. Therefore, using the technique of "doubling the circle", we turn to the line.
1. If some segment R [i] <L [i], then we make R [i] + = M.
2. For any segment L [i] .. R [i], we generate a pair L [i] + M..R [i] + M
Now we have 2n segments on the line, and a circle with a cut at the point x corresponds to a segment of this line [x..x + M), where 0 <= x <M.
Solution of problem 2 for O (sort + n 2 ) . Sort the segments at the right end once, then iterate through n possible points of the cut R [i], solving for each the problem in O (n), as well as Problem 1 .
Solution of problem 2 in O (sort + nk) , where k is the size of the set-answer to the problem. Leave the sort.
And immediately after sorting, we use the method of two pointers and for O (n) for each segment i we calculate the next segment next [i], which we would take as our greed (greed: L [next [i]]> R [i]) next [i] = min).
Now we make an interesting observation: depending on the cut point, the size of the set obtained by us differs from the optimal one by no more than 1. That is, if we cut at the first available point and get a set of size k, we just need to find a set of size k-1, and it sure to be optimal.
Solution: iterate over the first segment, take k-2 steps forward using next links, if the distance between the rightmost and leftmost point is less than M, we found k-1 disjoint arcs.
Solution for O (sort + n)
Take times the random point i = random [0..n-1]. For each i in O (k), we try a = next [i], as in the code above.
times the random point i = random [0..n-1]. For each i in O (k), we try a = next [i], as in the code above.
Since, if the answer from k-1 segments exists, it was enough for us to get into any one of these k-1, then the probability that attempts we never got equal
attempts we never got equal 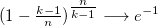 at
at  tending to infinity. Note that if
tending to infinity. Note that if  = Θ (1), then the previous algorithm for O (nk) completely suits us. Those. we obtained a probabilistic algorithm whose operation time is O (sort + n). To achieve the best e -T error, just try not to
= Θ (1), then the previous algorithm for O (nk) completely suits us. Those. we obtained a probabilistic algorithm whose operation time is O (sort + n). To achieve the best e -T error, just try not to  , but
, but 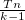 points, the running time will be respectively O (sort + Tn).
points, the running time will be respectively O (sort + Tn).
Not always on a certain topic sufficiently ready tasks, regularly have to invent new ones. We have just observed a funny effect: we take the classic simple sorting problem, replace the “straight line” with the “circle”, we get the complicated task of the two-pointer method and the probabilistic idea. Many beautiful learning tasks are invented. By the way, try to solve two more problems:
Problem 3. Given n segments on a line, choose the largest subset of segments such that each point is covered no more than k times (we just solved it for k = 1).
Task 4. Given n arcs (segments) on a circle ... and the same task.
If you like the tasks, you can find about hundreds of tasks for the fall and spring semester of this year using the links autumn and spring . Some tasks attached analysis.
Today I want to share with you two tasks from these seminars.
Problem 1. On the line are given n segments, you need to choose the maximum size of the subset of non-intersecting.
')
Task 2. On the circle there are n arcs (segments), you need to choose the maximum size of the subset of non-intersecting.
The first task is one of the examples on the topic of “greedy algorithms”. The solution can be viewed below. In short, the solution is supposed to be sorted by O (sort + n). Here, for sort, I denote the time to sort an array of length n. By the way, sort is optional nlogn (for example, bucket sort, radix sort, input data from a limited range).
The second problem has a beautiful probabilistic solution for O (sort + n). Despite its similarity to the first, the second task is not solved by greed in the forehead. Rather, I personally do not know the greedy decision, if someone from the readers comes up with and shares, I will be glad to listen. And in order to make it easier to think, I will immediately describe several non-working ideas that most often come up when trying to solve this problem:
- Suppose there is a point on the circle that is not covered by any segment, then the circle can be cut at this point and get the problem about the straight line, which we can already solve!
Yes. But such points may not be. Moreover, each point of a circle can be covered by 2, 10, or even Θ (n) segments - Cut the circle on the point covered with the minimum number of segments!
Does not work. Imagine 3 divisions of a circle into 10 segments. Only 30 segments. In two of these “splits”, the segments overlap slightly. We need to guess the third of the splits and select the end of one of these 10 segments as the cut point. - It is advantageous to take in response the shortest segment!
Not. Even on the straight is no longer true: (0,49) (50,100) (48,51) - It is advantageous to throw out from the set the longest segment that crosses someone!
Not. See the previous example. - And also ...
There are a lot of non-working ideas, let's stop the listing on those already voiced.
Problem solving
Problem solving 1.
Each segment i has a left end L [i] and a right end R [i]. We sort the segments in ascending order R [i]. In this order, we will go through the segments. The next segment will be added to the response if its left border is greater than the maximum of the right borders of already added segments.
Problem solving 2.
I warn you, the solution is long and much more complicated than the previous one. On the other hand, there are no fundamentally complex ideas here, so everything can be understood without initial preparation.
For a start, let's say how arcs are defined on a circle. Let the circle be the looped segment [0..M), and the arcs (segments) of the circle are given by the pairs L [i] .. R [i]. If R [i] <L [i], the segment passes through the point M.
The main idea of the solution is to find a point where a circle can be cut. Or rather, choose the segment i, which we will definitely take in response. As soon as such segment i is fixed, the circle can be cut, for example at the point R [i].
Representing all objects on a circle, solving a problem is not very convenient. Therefore, using the technique of "doubling the circle", we turn to the line.
1. If some segment R [i] <L [i], then we make R [i] + = M.
2. For any segment L [i] .. R [i], we generate a pair L [i] + M..R [i] + M
Now we have 2n segments on the line, and a circle with a cut at the point x corresponds to a segment of this line [x..x + M), where 0 <= x <M.
Solution of problem 2 for O (sort + n 2 ) . Sort the segments at the right end once, then iterate through n possible points of the cut R [i], solving for each the problem in O (n), as well as Problem 1 .
Solution of problem 2 in O (sort + nk) , where k is the size of the set-answer to the problem. Leave the sort.
And immediately after sorting, we use the method of two pointers and for O (n) for each segment i we calculate the next segment next [i], which we would take as our greed (greed: L [next [i]]> R [i]) next [i] = min).
// b = 0; for (a = 0; a < n; a++) { while (L[b] <= R[a]) b++; // b 2n next[a] = b; } Now we make an interesting observation: depending on the cut point, the size of the set obtained by us differs from the optimal one by no more than 1. That is, if we cut at the first available point and get a set of size k, we just need to find a set of size k-1, and it sure to be optimal.
Solution: iterate over the first segment, take k-2 steps forward using next links, if the distance between the rightmost and leftmost point is less than M, we found k-1 disjoint arcs.
for (a = 0; a < n; a++) { b = a; for (i = 0; i < k - 2; i++) b = next[b]; if (R[b] - L[a] < M) ; // , k-1 ! a, next[a], next[next[a]] ... b } Solution for O (sort + n)
Take
Since, if the answer from k-1 segments exists, it was enough for us to get into any one of these k-1, then the probability that
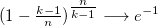 at
at 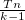 points, the running time will be respectively O (sort + Tn).
points, the running time will be respectively O (sort + Tn).Epilogue
Not always on a certain topic sufficiently ready tasks, regularly have to invent new ones. We have just observed a funny effect: we take the classic simple sorting problem, replace the “straight line” with the “circle”, we get the complicated task of the two-pointer method and the probabilistic idea. Many beautiful learning tasks are invented. By the way, try to solve two more problems:
Problem 3. Given n segments on a line, choose the largest subset of segments such that each point is covered no more than k times (we just solved it for k = 1).
Task 4. Given n arcs (segments) on a circle ... and the same task.
More tasks
If you like the tasks, you can find about hundreds of tasks for the fall and spring semester of this year using the links autumn and spring . Some tasks attached analysis.
Source: https://habr.com/ru/post/254093/
All Articles