Planets and the fourth dimension
You probably know that the planets move around the sun in elliptical orbits. But why? In fact, they move in circles in four-dimensional space. And if you project these circles into three-dimensional space, they turn into ellipses.

In the figure, a plane denotes 2 of 3 dimensions of our space. The vertical direction is the fourth dimension. The planet moves in a circle in four-dimensional space, and its “shadow” in three-dimensional moves in an ellipse.
')
What is this 4th dimension? It looks like time, but it is not exactly time. This is such a special time that flows at a rate inversely proportional to the distance between the planet and the sun. And relative to this time, the planet moves at a constant speed in a circle in 4 dimensions. And in normal time, his shadow in three dimensions moves faster when it is closer to the sun.
It sounds weird - but this is just an unusual way of representing ordinary Newtonian physics. This method has been known since at least 1980, thanks to the work of mathematical physicist Jürgen Moser. And I found out about this by getting an email to work for the authorship of Jesper Goranson called “Symmetries in the Kepler Problem” (March 8, 2015).
The most interesting thing in this work - this approach explains one interesting fact. If we take any elliptical orbit, and rotate it in 4-dimensional space, we get another valid orbit.
Of course, you can rotate an elliptical orbit around the sun and in ordinary space, getting a valid orbit. It is interesting that this can be done in 4-dimensional space, for example, by narrowing or widening an ellipse.
In general, any elliptical orbit can be turned into any other. All orbits with the same energy are circular orbits on the same sphere in 4-dimensional space.
Kepler's task
Suppose we have a particle that moves according to the inverse square law. The equation of its motion will be

where r is the position as a function of time, r is the distance from the center, m is the mass, and k determines the force. From here you can derive the law of energy conservation

for some constant E, depending on the orbit, but not changing with time. If this force is an attraction, then k> 0, and in an elliptical orbit E <0. We call the particle a planet. The planet moves around the sun, which is so heavy that its vibrations can be neglected.
We will explore orbits with one energy E. Therefore, units of mass, length and time can be taken as any. Set
m = 1, k = 1, E = -1/2
This will save us from unnecessary letters. Now the equation of motion looks like
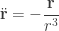
and the conservation law says

Now, following the idea of Moser, let's move from the usual time to the new. Call it s and require that

This time goes slower as you move away from the sun. Therefore, the speed of the planet to distance from the sun increases. This compensates for the tendency of the planets to move as they move away from the sun more slowly in normal time.
Now rewrite the law of conservation with the help of the new time. Since I used a point for the derivatives of the usual time, let's use the stroke for the time derivatives of s. Then for example:

and

Using such a derivative, Goranson shows that energy conservation can be written as

And this is nothing but the equation of the four-dimensional sphere. Proof will be later. Now let's talk about what it means to us. To do this, we need to combine the usual time coordinate t with the spatial coordinates (x, y, z). Point
(t, x, y, z)
moves in four-dimensional space as s changes. That is, the speed of this point, namely

moves in a four-dimensional sphere. This is a sphere of radius 1 centered at
(1,0,0,0)
Additional calculations show other interesting facts:

and
t '' '= - (t' - 1)
These are the usual equations of a harmonic oscillator, but with an additional derivative. The proof will be later, but for now we will think what it means. In words, this can be described as follows: 4-dimensional velocity v performs simple harmonic oscillations around a point (1,0,0,0).
But since v at the same time remains on a sphere with a center at this point, we can conclude that v moves at a constant speed in a circle on this sphere. This implies that the average value of the spatial components of the 4-dimensional velocity is 0, and the average t is 1.
The first part is clear: our planet, on average, does not fly away from the Sun, therefore its average speed is zero. The second part is more complicated: the usual time t moves forward with an average speed of 1 relative to the new time s, but its rate of change varies sinusoidally.
Integrating both parts

we'll get

for some constant vector a . The equation says that the position r harmonically oscillates around point a . Since a does not change with time, this is a conserved value. This is called the Laplace – Runge – Lenz vector.
Often people start with the inverse square law, show that the angular momentum and the Laplace-Runge vector are preserved, and use these conserved quantities and the Noether theorem to show the presence of a 6-dimensional symmetry group. For solutions with negative energy, this turns into a turn group in 4 dimensions, SO (4). After working a little more, you can see how Kepler’s task is associated with a harmonic oscillator in 4 dimensions. This is done through time reparameterization.
I liked Gorasnon’s approach more, because it begins with the reparameterization of time. This allows us to effectively show that the elliptical orbit of the planet is a projection of a circular orbit in four-dimensional space on three-dimensional. Thus, 4-dimensional rotational symmetry becomes apparent.
Goranson transfers this approach to the inverse square law in n-dimensional space. It turns out that elliptical orbits in n dimensions are projections of circular orbits from n + 1 dimensions.
It also applies this approach to positive energy orbits, which are hyperbolas, and zero-energy orbits (parabolas). In hyperbolas, the symmetry of the Lorentz groups is obtained, and in parabolas, the symmetry of Euclidean groups. This is a well-known fact, but it is remarkable how simple it is to derive it with the help of a new approach.
Math details
Because of the abundance of equations, I set a framework around important equations. The basic equations are energy conservation, force and change of variables, which give:

We start with energy conservation:

then use

To obtain

A bit of algebra - and we get

This shows that 4-dimensional speed

remains on a sphere of unit radius with center at (1,0,0,0).
The next step is to take the equation of motion.

and rewrite it using dashes (derivatives with respect to s), rather than points (derivatives with respect to t). Starting with

and differentiate to get

Now use another equation for

and get

or

so

Now it would be good to get the formula for r ". We first calculate

and then differentiate

Connect the formula for r ", something will shrink, and we will get

Recall that conservation law says

and we know that t '= r. Therefore,

and

Get

Since t '= r, it turns out

as we need.
Now we get a similar formula for r '' ' . Let's start with

and differentiate

Let's connect formulas for r '' and r '' '. Something shrinks, and remains

We integrate both parts and get

for some constant vector a . This means that r harmonically oscillates with respect to a . It is interesting that both the vector r and its norm r oscillate harmonically.
The quantum version of the planetary orbit is a hydrogen atom. Everything that we considered can be used in the quantum version. See Greg Egan, The ellipse and the atom for details.
For details on the history of this task, see John Baez, Mysteries of the gravitational 2-body problem .
And all this also relates to quantum physics, supersymmetry and Jordan algebra!

In the figure, a plane denotes 2 of 3 dimensions of our space. The vertical direction is the fourth dimension. The planet moves in a circle in four-dimensional space, and its “shadow” in three-dimensional moves in an ellipse.
')
What is this 4th dimension? It looks like time, but it is not exactly time. This is such a special time that flows at a rate inversely proportional to the distance between the planet and the sun. And relative to this time, the planet moves at a constant speed in a circle in 4 dimensions. And in normal time, his shadow in three dimensions moves faster when it is closer to the sun.
It sounds weird - but this is just an unusual way of representing ordinary Newtonian physics. This method has been known since at least 1980, thanks to the work of mathematical physicist Jürgen Moser. And I found out about this by getting an email to work for the authorship of Jesper Goranson called “Symmetries in the Kepler Problem” (March 8, 2015).
The most interesting thing in this work - this approach explains one interesting fact. If we take any elliptical orbit, and rotate it in 4-dimensional space, we get another valid orbit.
Of course, you can rotate an elliptical orbit around the sun and in ordinary space, getting a valid orbit. It is interesting that this can be done in 4-dimensional space, for example, by narrowing or widening an ellipse.
In general, any elliptical orbit can be turned into any other. All orbits with the same energy are circular orbits on the same sphere in 4-dimensional space.
Kepler's task
Suppose we have a particle that moves according to the inverse square law. The equation of its motion will be

where r is the position as a function of time, r is the distance from the center, m is the mass, and k determines the force. From here you can derive the law of energy conservation

for some constant E, depending on the orbit, but not changing with time. If this force is an attraction, then k> 0, and in an elliptical orbit E <0. We call the particle a planet. The planet moves around the sun, which is so heavy that its vibrations can be neglected.
We will explore orbits with one energy E. Therefore, units of mass, length and time can be taken as any. Set
m = 1, k = 1, E = -1/2
This will save us from unnecessary letters. Now the equation of motion looks like
and the conservation law says

Now, following the idea of Moser, let's move from the usual time to the new. Call it s and require that

This time goes slower as you move away from the sun. Therefore, the speed of the planet to distance from the sun increases. This compensates for the tendency of the planets to move as they move away from the sun more slowly in normal time.
Now rewrite the law of conservation with the help of the new time. Since I used a point for the derivatives of the usual time, let's use the stroke for the time derivatives of s. Then for example:

and

Using such a derivative, Goranson shows that energy conservation can be written as

And this is nothing but the equation of the four-dimensional sphere. Proof will be later. Now let's talk about what it means to us. To do this, we need to combine the usual time coordinate t with the spatial coordinates (x, y, z). Point
(t, x, y, z)
moves in four-dimensional space as s changes. That is, the speed of this point, namely

moves in a four-dimensional sphere. This is a sphere of radius 1 centered at
(1,0,0,0)
Additional calculations show other interesting facts:

and
t '' '= - (t' - 1)
These are the usual equations of a harmonic oscillator, but with an additional derivative. The proof will be later, but for now we will think what it means. In words, this can be described as follows: 4-dimensional velocity v performs simple harmonic oscillations around a point (1,0,0,0).
But since v at the same time remains on a sphere with a center at this point, we can conclude that v moves at a constant speed in a circle on this sphere. This implies that the average value of the spatial components of the 4-dimensional velocity is 0, and the average t is 1.
The first part is clear: our planet, on average, does not fly away from the Sun, therefore its average speed is zero. The second part is more complicated: the usual time t moves forward with an average speed of 1 relative to the new time s, but its rate of change varies sinusoidally.
Integrating both parts

we'll get

for some constant vector a . The equation says that the position r harmonically oscillates around point a . Since a does not change with time, this is a conserved value. This is called the Laplace – Runge – Lenz vector.
Often people start with the inverse square law, show that the angular momentum and the Laplace-Runge vector are preserved, and use these conserved quantities and the Noether theorem to show the presence of a 6-dimensional symmetry group. For solutions with negative energy, this turns into a turn group in 4 dimensions, SO (4). After working a little more, you can see how Kepler’s task is associated with a harmonic oscillator in 4 dimensions. This is done through time reparameterization.
I liked Gorasnon’s approach more, because it begins with the reparameterization of time. This allows us to effectively show that the elliptical orbit of the planet is a projection of a circular orbit in four-dimensional space on three-dimensional. Thus, 4-dimensional rotational symmetry becomes apparent.
Goranson transfers this approach to the inverse square law in n-dimensional space. It turns out that elliptical orbits in n dimensions are projections of circular orbits from n + 1 dimensions.
It also applies this approach to positive energy orbits, which are hyperbolas, and zero-energy orbits (parabolas). In hyperbolas, the symmetry of the Lorentz groups is obtained, and in parabolas, the symmetry of Euclidean groups. This is a well-known fact, but it is remarkable how simple it is to derive it with the help of a new approach.
Math details
Because of the abundance of equations, I set a framework around important equations. The basic equations are energy conservation, force and change of variables, which give:

We start with energy conservation:

then use

To obtain

A bit of algebra - and we get

This shows that 4-dimensional speed

remains on a sphere of unit radius with center at (1,0,0,0).
The next step is to take the equation of motion.

and rewrite it using dashes (derivatives with respect to s), rather than points (derivatives with respect to t). Starting with

and differentiate to get

Now use another equation for

and get

or

so

Now it would be good to get the formula for r ". We first calculate

and then differentiate

Connect the formula for r ", something will shrink, and we will get

Recall that conservation law says

and we know that t '= r. Therefore,

and

Get

Since t '= r, it turns out

as we need.
Now we get a similar formula for r '' ' . Let's start with

and differentiate

Let's connect formulas for r '' and r '' '. Something shrinks, and remains

We integrate both parts and get

for some constant vector a . This means that r harmonically oscillates with respect to a . It is interesting that both the vector r and its norm r oscillate harmonically.
The quantum version of the planetary orbit is a hydrogen atom. Everything that we considered can be used in the quantum version. See Greg Egan, The ellipse and the atom for details.
For details on the history of this task, see John Baez, Mysteries of the gravitational 2-body problem .
And all this also relates to quantum physics, supersymmetry and Jordan algebra!
Source: https://habr.com/ru/post/254023/
All Articles