Spectral analysis of signals

Not so long ago, Comrade Makeman described how, using spectral analysis, you can decompose some sound signal into its composing notes. Let's abstract a little from a sound and we suppose that we have some digitized signal, which spectral structure we want to define, and precisely enough.

Under the cat a brief overview of the method of harmonic selection from an arbitrary signal using digital heterodyning, and a little special, Fourier magic.

So, what we have.
File with samples of the digitized signal. It is known that a signal is the sum of sinusoids with its own frequencies, amplitudes and initial phases, and, possibly, white noise.
')
What do we do.
Use spectral analysis to determine:

• the number of harmonics in the signal, and for each: amplitude, frequency (hereinafter in the context of the number of wavelengths per signal length), the initial phase;
• presence / absence of white noise, and, if available, its MSE (standard deviation);
• the presence / absence of a constant component of the signal;
• put all this into a pretty PDF report with blackjack and illustrations.

We will solve this problem in Java.

Materiel

As I have already said, the signal structure is obviously known: it is the sum of sinusoids and some noise component. It so happened that for the analysis of periodic signals in engineering practice they widely use a powerful mathematical apparatus, generally referred to as “Fourier analysis” . Let's take a quick look at what this kind of beast is.

Bit special, Fourier Magic

Not so long ago, in the 19th century, the French mathematician Jean Baptiste Joseph Fourier showed that any function satisfying certain conditions (continuity in time, periodicity, satisfaction of Dirichlet conditions) can be decomposed into a series, which later received his name - the Fourier series .

In engineering practice, the decomposition of periodic functions in a Fourier series is widely used, for example, in problems of circuit theory: a non-sinusoidal input action is decomposed into a sum of sinusoidal and the necessary parameters of the circuits are calculated, for example, by the overlay method.

There are several possible options for recording the coefficients of the Fourier series, we only need to know the essence.
Fourier series decomposition allows decomposing a continuous function into the sum of other continuous functions. And in general, the series will have an infinite number of members.

A further improvement of the Fourier approach is the integral transformation of his own name. Fourier transform .
In contrast to the Fourier series, the Fourier transform decomposes the function not according to discrete frequencies (the set of frequencies of the Fourier series over which decomposition occurs, generally speaking, discrete), but into continuous ones.
Let's take a look at how the coefficients of the Fourier series and the result of the Fourier transform, referred to as the spectrum , correlate.
A small digression: the Fourier transform spectrum is, in general, a complex function that describes the complex amplitudes of the corresponding harmonics. That is, the spectrum values ​​are complex numbers, whose modules are amplitudes of the corresponding frequencies, and the arguments are the corresponding initial phases. In practice, the amplitude spectrum and the phase spectrum are considered separately.


Fig. 1. The correspondence of the Fourier series and Fourier transforms on the example of the amplitude spectrum.

It is easy to see that the coefficients of the Fourier series are nothing more than the values ​​of the Fourier transform at discrete points in time.

However, the Fourier transform associates a continuous in time, infinite function of another, continuous in frequency, infinite function - the spectrum. What if we do not have a function that is infinite in time, but there is only some part of it that is discrete in time recorded? The answer to this question is provided by the further development of the Fourier transform - the discrete Fourier transform (DFT) .

The discrete Fourier transform is designed to solve the problem of the need for continuity and infinity in time of a signal. In fact, we believe that we cut out some part of the infinite signal, and the rest of the time domain we consider this signal to be zero.

Mathematically, this means that, having a function f (t) that is endless in time, we multiply it by a window function w (t), which vanishes everywhere except for the time interval of interest.

If the "output" of the classical Fourier transform is the spectrum - function, then the "output" of the discrete Fourier transform is the discrete spectrum. And the input is also fed samples of a discrete signal.

The remaining properties of the Fourier transform do not change: you can read about them in the relevant literature.

We only need to know about the Fourier transform of a sinusoidal signal, which we will try to find in our spectrum. In general, this is a pair of delta functions that are symmetrical about the zero frequency in the frequency domain.


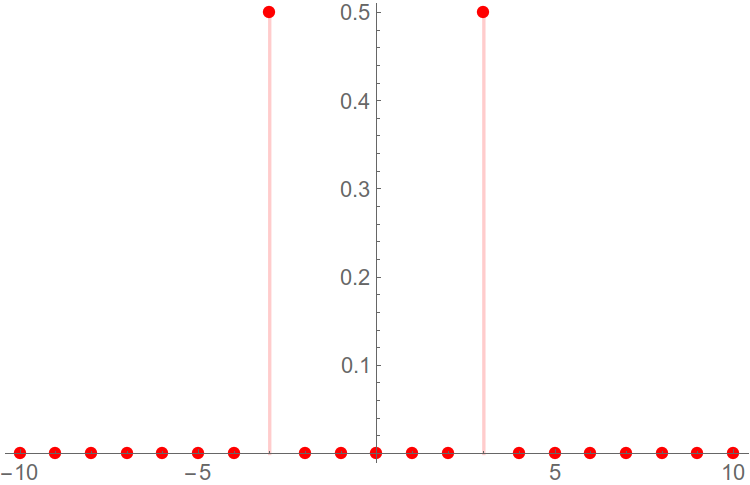
Fig. 2. Amplitude spectrum of a sinusoidal signal.

I have already mentioned that, generally speaking, we are not considering the original function, but some of its product with a window function. Then, if the spectrum of the original function is F (w), and the window W (w), then the spectrum of the product will be such an unpleasant operation as the convolution of these two spectra (F * W) (w) (The convolution theorem).

In practice, this means that instead of the delta function, in the spectrum we will see something like this:


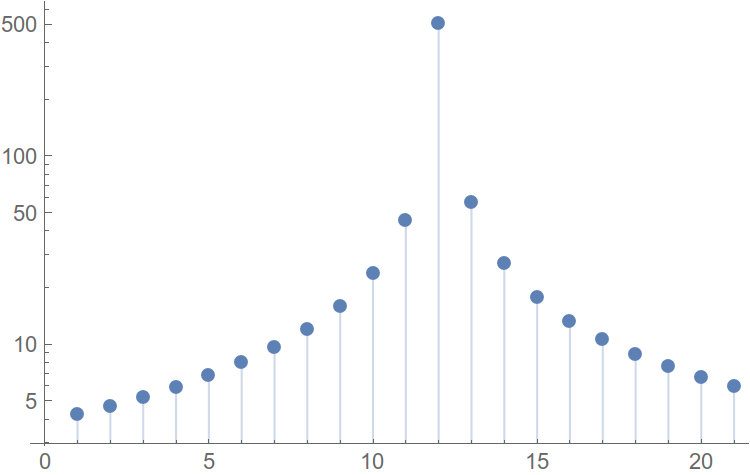
Fig. 3. The effect of spreading the spectrum.

This effect is also called spectral leekage. And the noise that appears as a result of spreading the spectrum, respectively, side lobes (eng. Sidelobes).
To combat side lobes use other, non-rectangular window functions. The main characteristic of the "efficiency" of the window function is the level of side lobes (dB). A summary table of side-lobe levels for some commonly used window functions is shown below.

Window function	Side lobe level (dB)
Dirichlet window (rectangular window)	-13 dB
Window hannah	-31.5 dB
Hamming window	-42 dB

The main problem in our problem is that side lobes can mask other harmonics lying side by side.


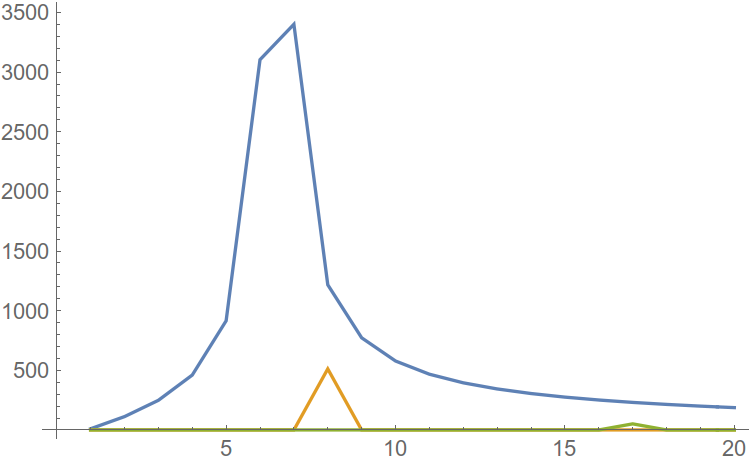
Fig. 4. Separate harmonic spectra.

It is seen that when adding the above spectra, the weaker harmonics seem to dissolve into the stronger one.


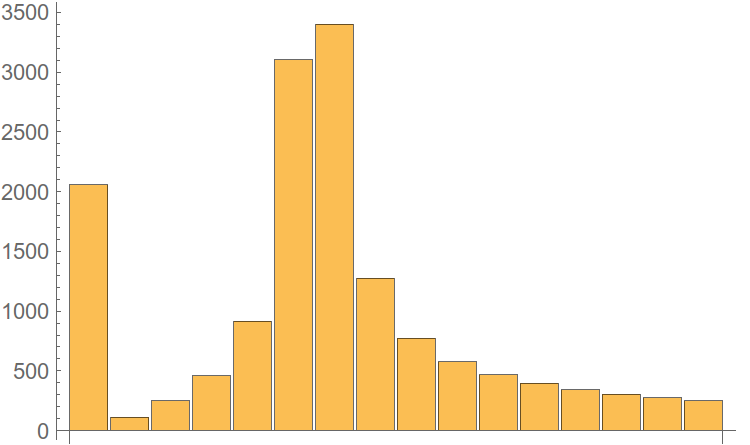
Fig. 5. Only one harmonic is clearly visible. Not good.

Another approach to combating spreading the spectrum is to subtract from the signal the harmonics that create this spreading.
That is, by setting the amplitude, frequency and initial phase of the harmonic, you can subtract it from the signal, and we will remove the “delta function” corresponding to it, and with it the side lobes generated by it. Another question is how to exactly know the parameters of the desired harmonic. It is not enough to simply take the necessary data from the complex amplitude. The complex amplitudes of the spectrum are formed at integral frequencies, however, nothing prevents the harmonic from having a fractional frequency. In this case, the complex amplitude seems to spread between two adjacent frequencies, and its exact frequency, like other parameters, cannot be set.

To establish the exact frequency and complex amplitude of the desired harmonic, we will use a technique widely used in many branches of engineering practice - heterodyning .

Let's see what happens if we multiply the input signal by the complex harmonic Exp (I * w * t). The signal spectrum will shift by the value of w to the right.
We will use this property by shifting the spectrum of our signal to the right until the harmonic resembles the delta function even more (that is, until some local signal-to-noise ratio reaches its maximum). Then we can calculate the exact frequency of the desired harmonic, such as w ₀ - w _het , and subtract it from the original signal to suppress the spreading effect of the spectrum.
An illustration of the change in spectrum depending on the LO frequency is shown below.


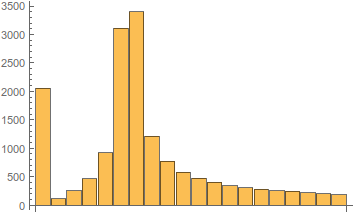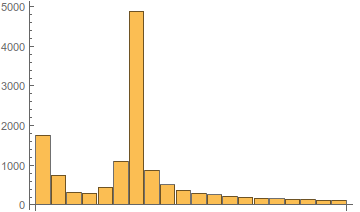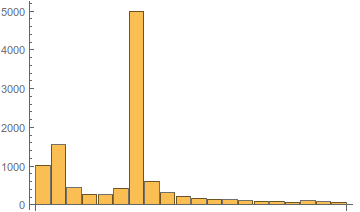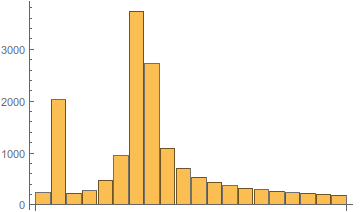
Fig. 6. Type of amplitude spectrum depending on the frequency of the local oscillator.

We will repeat the described procedures until we cut out all the harmonics present, and the spectrum does not remind us of the spectrum of white noise.

Then, you need to evaluate the standard deviation of white noise. Tricks are not here: you can simply use the formula for calculating the deviations:

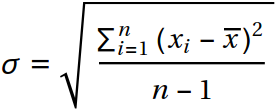
Automate it

It's time to automate the harmonic extraction. Repeat one more time algorithm:

1. We are looking for a global peak of the amplitude spectrum, above a certain threshold k.
1.1 If not found, finish
2. By varying the frequency of the local oscillator, we are looking for a value of the frequency at which the maximum of some local signal-to-noise ratio will be reached in a certain neighborhood of the peak
3. If necessary, round off the amplitude and phase values.
4. Subtract the harmonic from the signal with the found frequency, amplitude and phase minus the local oscillator frequency.
5. Go to step 1.

The algorithm is not complicated, and the only question that arises is where do we get the threshold values, above which we will look for harmonics?
To answer this question, you should estimate the noise level before cutting out the harmonics.

We construct the distribution function (hello, mate. Statistics), where the amplitude of the harmonics will be on the abscissa axis, and the number of harmonics not exceeding in amplitude will be the very value of the argument on the ordinate axis. An example of such a constructed function:


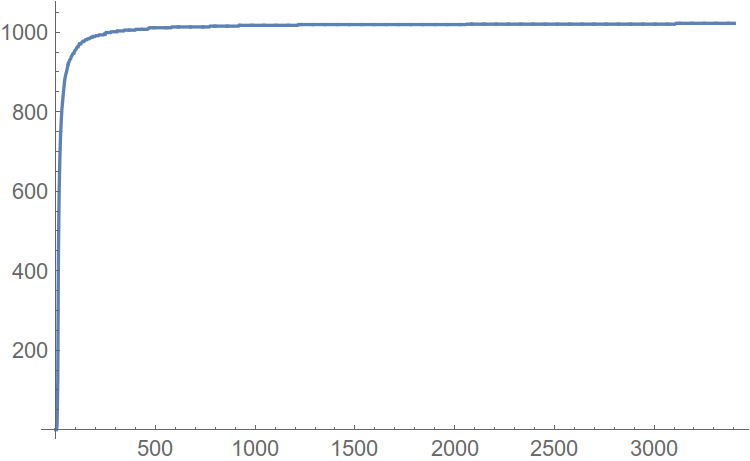
Fig. 7. Harmonic distribution function.

Now we also construct a function - the distribution density. That is, the values ​​of finite differences from the distribution function.


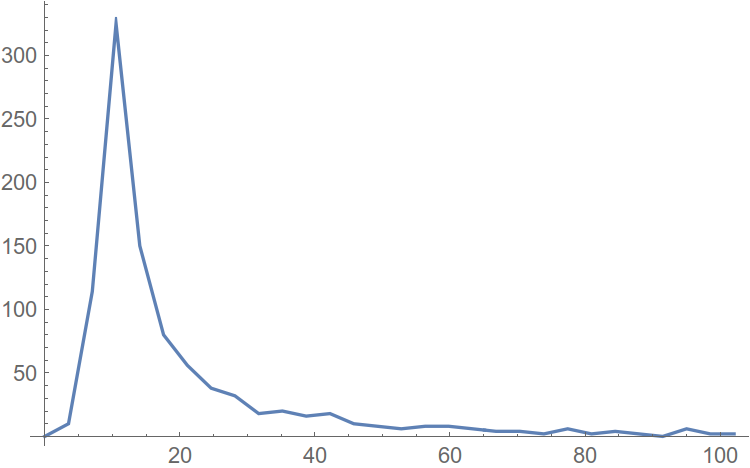
Fig. 8. Density of the harmonic distribution function.

The abscissa of the distribution density maximum is the amplitude of the harmonic occurring in the spectrum the greatest number of times. Let's move away from the peak to the right for some distance, and we will consider the abscissa of this point as an estimate of the noise level in our spectrum. Now you can and automate.

Practical part

I do not claim to be a Java expert, and the solution presented can be questionable both in terms of performance and memory consumption, and in general, Java philosophy and OOP philosophy, no matter how hard I try to make it better. It was written for a couple of evenings, as proof of concept. Those interested can see the source code on GitHub .

The only difficulty was the generation of a PDF report on the results of the analysis: the PDFbox didn’t want to work with Cyrillic. By the way, does not want now.

The project used libraries:
JFreeChart - display charts
PDFBox - report building
JLatexMath - Rendering Latex Formulas

As a result, a rather massive program (13.6 megabytes) turned out, which conveniently implements the task.

It is possible to cut the harmonics manually, and entrust this task to the algorithm.

Thank you all for your attention!


Sample report created by the program .

Literature

A. B. Sergienko - Digital Signal Processing