Where is the death of Kashcheev?
Hi guys, let's check your memory first. So:
 And now, attention, the question is - how to formalize it?
And now, attention, the question is - how to formalize it?
How to attach a needle to the egg and what is the temporary complexity of the detail of my death. How to transfer a fairy tale to reality, how it looks on B-trees and why there really is no difference between 2D and 1D.
But it was like this: a long time ago, in a certain kingdom, in a certain state, Ivanushka the Fool at the CNC level wanted to divide Moscow (/ RU / MOW /) and Oblast (/ RU / MOS /) on the same service as georing. In general, restore order, so that everything lay on the shelves beautifully and alphabetically. But he could not count his treasures, and carefully decompose them. And Vasilisa, although a fool, did not allow her to save.
But the solution was found.
Not far above some gold chah Chahlik successfully, he also hid his death according to science.
And if the task of determining the regional (more precisely polygonal) belonging of a certain needle to a certain chest is beyond the scope of this article, then nothing prevents us from diving into the depths of the hare and seeing how it works on a tabular level.
PS: and do not ask why the hare.
So - the original task is to determine some entries in certain headings, but let's clarify the terms of reference:
In general, the task is to process certain elements that are tied to a certain tree of hierarchies.
Let's start with a simple one - and the implementation of headings, directories or just trees. There are not many implementation options, more precisely, a normalized implementation option in general seems to be one:
There is a certain element, and it has one parent (if two are no longer trees). This all works well as long as we do not need to perform some operations on branches .
')
These problems are also relevant for rubrics on the site, and files on the disk, and generally purely theoretical sofa surveys.
And there are several standard solutions to this problem:

But that’s what we’ll understand, because the Nested set table ( http://en.wikipedia.org/wiki/Nested_set_model ) is :

The difference from the "normal" child-parent schemes is that a certain parent contains two certain "numbers" - the beginning of its interval, and the end. And all his children contain "numbers" somewhere between these values. You can visualize in different ways, in Wikipedia you can find several scary options for trees. But if you take a regular tree, divide by levels and draw on a piece of paper - you get lists with gaps.
And with a flick of a wand, this picture turns into a B-tree. Because there is no difference ideologically.
In some way, nested-set addressing can be considered a kind of “space filling curve”, a kind of curve that inextricably recursively intersects all elements of a certain tree in traversal order.
If the initial interval is set to 0-1, then divided at 1/2, then 1 / 4.2 / 4.3 / 4.8 / 16.50 / 128 ... then it turns out that any student who is in the first year tried to eat within the limits and converging sequence - smoked my weed. Although in reality it is called the Stern Tree - Brokaw

For many, the most difficult in NS is their construction. Many people are immediately scared by these left / right / st and other scary words and pictures used on various sites. Including on Habré you can find a couple of articles about building NS in a database, including on storages and triggers . Personally, such articles scare me.
In fact, NS is just intervals, just a statement that children can be found somewhere in the corridor of values of the parents. These are not trees, they are numbers that are stored in flat database tables. Continuous series on a numeric curve.
As a result, building NS can be easier:
Option 1:
Option 2:
In both cases, insertion and deletion is O (n), and sometimes O (1).
NS is just two numbers, the interval between the "buns" which is hidden all the most delicious. In the general case, the curve does not have to consist of integers; moreover, it fits perfectly on fractions. We take the already mentioned Stern - Brokaw and obtain the Koch curve.
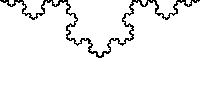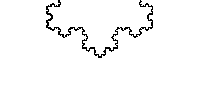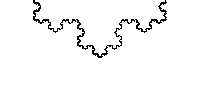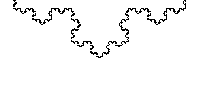
I hope you have read to this point, understand what the nested intervals are, it remains to understand why they are so good.
Imagine that you have a list of all hotels at the Hotellook (Aviasales). Imagine that you have a binding of these hotels in the country-region-city-district. The task is to find all hotels in Orekhovo-Borisovo South (narrow selection), all 5 star hotels in Turkey (large selection), and all hotels in a square 100 meters away from you.
Solution 1:
Solution of situation 2:
That's the secret - there is no difference . And in both cases it works quickly.
Solving situation 3 implies some kind of coordinate search . But in ordinary databases, this is a very complicated and expensive operation — a double-key search, or a 2D (spatial) key is simply difficult, expensive, and many reads are generated from different places of the disk. Well, simply because the order of data storage on disk 1D.
But the solution to the situation remains almost the same:
Where we use Morton, it's Z-curve code for converting 2D coordinates to 1D curve (this was written on Habré a couple of times), and then save it in Gray codes (two bits per division) and we can make quick samples along the pyramid ( Hello ObjectManager ).
For many, it is not entirely clear why the samples are fast - you should probably explain. Morton codes, besides being “addressing by quadtree”, have another property - codes for objects that are close by will be near.
Z is not the best solution, but it is great for quick samples of groups (tiles) of objects. Z-codes "hold" the locality of the data, including for objects of one node, the codes will be generally the same, or their variability will be clamped between the left and right values of the NS element.
Plus - NS, as I said before - some materialization of skip-sheets, a numerical curve or even B-trees. Technically, there is no difference. So, when you store data in NS, you store it in B-tree ... then ... wait ...
In general, Z , Hilbert , GeoHash (Z codes in base64) and the company are the sameI NestedSet, view from the side.
These codes are often used in various GIS systems, including Bing called their quad-code and uses for addressing tiles, and all this works without problems in 3D and in 4D space.
By reducing puzzles in a simple numeric curve.
And in the standard NestedSet.

The effect is always the same - everything starts working .
Here and the fairy tale is over, and who listened - well done.
PS: With you there were kashey and esosedi, who have been using NS and Z codes for sampling objects on the map for almost 7 years. Among which are HotelLook hotels (which are special.habrahabr.ru/aviasales ).
PPS: Join the Fourier series - convergence! Equality! Hilbert space!
PPPS: And don't forget the wisdom of the ages!
“There is an island on the sea on the ocean, on that island there is an oak tree, a chest is buried under an oak tree, a hare is in a chest, a duck is in a hare, an egg is in an egg” Koschei’s death is in an egg!
 And now, attention, the question is - how to formalize it?
And now, attention, the question is - how to formalize it?How to attach a needle to the egg and what is the temporary complexity of the detail of my death. How to transfer a fairy tale to reality, how it looks on B-trees and why there really is no difference between 2D and 1D.
But it was like this: a long time ago, in a certain kingdom, in a certain state, Ivanushka the Fool at the CNC level wanted to divide Moscow (/ RU / MOW /) and Oblast (/ RU / MOS /) on the same service as georing. In general, restore order, so that everything lay on the shelves beautifully and alphabetically. But he could not count his treasures, and carefully decompose them. And Vasilisa, although a fool, did not allow her to save.
But the solution was found.
Not far above some gold chah Chahlik successfully, he also hid his death according to science.
And if the task of determining the regional (more precisely polygonal) belonging of a certain needle to a certain chest is beyond the scope of this article, then nothing prevents us from diving into the depths of the hare and seeing how it works on a tabular level.
PS: and do not ask why the hare.
So - the original task is to determine some entries in certain headings, but let's clarify the terms of reference:
- There is a " sheyring with geolocation " - about 3 million points
- Which somehow "lie" in 300 thousand blocks, districts and other administrative divisions, nested in each other.
- At any time you want to find all the objects included in at least the area of the city, even in the continent.
In general, the task is to process certain elements that are tied to a certain tree of hierarchies.
Let's start with a simple one - and the implementation of headings, directories or just trees. There are not many implementation options, more precisely, a normalized implementation option in general seems to be one:
{ id: entity_id, parent: parentId } There is a certain element, and it has one parent (if two are no longer trees). This all works well as long as we do not need to perform some operations on branches .
- 1. Find all subheadings == find all areas of the city
- 2. Find all the items in the subheadings == find all the objects of the city
- 3. Find all your parents to the top == to understand in which country the city
- 4. To count, aggregate, break or repair something.
')
These problems are also relevant for rubrics on the site, and files on the disk, and generally purely theoretical sofa surveys.
And there are several standard solutions to this problem:

- 1. Adjacent Set (AL) - en.wikipedia.org/wiki/Adjacency_list
A table of the form child, parent [, level], where all parents of the desired child are simply listed. How many parents - how many and records.
This is the easiest and most "normalized" option. Absolutely convenient, but it can serve very large “clouds” on the “exit” and generate kilometer-long “guts” of the tables. Because of its large size and smearing, it works, in general, not instantly. - 2. Materialized Path (MP)
This is when we take all our parents and “materialize” in one line, separated by commas. And then we can use the LIKE operator to find the right one.
In principle, the normal version, beloved by students. Especially good if you move from base 10, including the regular line, to a slightly more binary (base32,64,92 or 254).
Only one minus is not technological, and the indices in an arbitrary place of the line do not work very well.
PS: there are technological solutions - the so-called matrix trees, when the node ID is a matrix, and the position of the elements are the determinants of their multiplication. Given the non-commutativity of multiplication, the key turns out to be real. If, after reading this paragraph, you thought about Tin - so it is. - 3. Nested set (NS).
Nested set table is such a thing that many have heard about, but few know how it works and why. For many, NS is a plugin or library that can be used. And to understand - broke.
But that’s what we’ll understand, because the Nested set table ( http://en.wikipedia.org/wiki/Nested_set_model ) is :

- 1. One of the materializations skip-list
- 2. One of the materializations of B-tree
- 3. In direct translation, simply - nested intervals
- 4. They are not scary at all.
- 5. Provide linear storage.
- 6. And they are exactly what we need.
The difference from the "normal" child-parent schemes is that a certain parent contains two certain "numbers" - the beginning of its interval, and the end. And all his children contain "numbers" somewhere between these values. You can visualize in different ways, in Wikipedia you can find several scary options for trees. But if you take a regular tree, divide by levels and draw on a piece of paper - you get lists with gaps.
 |  |
And with a flick of a wand, this picture turns into a B-tree. Because there is no difference ideologically.
In some way, nested-set addressing can be considered a kind of “space filling curve”, a kind of curve that inextricably recursively intersects all elements of a certain tree in traversal order.
If the initial interval is set to 0-1, then divided at 1/2, then 1 / 4.2 / 4.3 / 4.8 / 16.50 / 128 ... then it turns out that any student who is in the first year tried to eat within the limits and converging sequence - smoked my weed. Although in reality it is called the Stern Tree - Brokaw

For many, the most difficult in NS is their construction. Many people are immediately scared by these left / right / st and other scary words and pictures used on various sites. Including on Habré you can find a couple of articles about building NS in a database, including on storages and triggers . Personally, such articles scare me.
In fact, NS is just intervals, just a statement that children can be found somewhere in the corridor of values of the parents. These are not trees, they are numbers that are stored in flat database tables. Continuous series on a numeric curve.
As a result, building NS can be easier:
Option 1:
In the database we count the number of our children (COUNT (id)), and then the amount of this number (count (count)). Thus, the “bubble method” full capacity rises to the top. It remains only to find your neighbor, and somehow take the offset from him - the full capacity of his neighbors to the left.
These are 4 SQL queries, some of which need to be executed a couple of times.
Okay, not 4
CREATE TABLE IF NOT EXISTS `flatindex` (`rid` int(11) NOT NULL,`lvl` tinyint(4) NOT NULL,`prev` int(11) NOT NULL,`parent` int(11) NOT NULL,`innerCnt` int(11) NOT NULL,`fullCnt` int(11) NOT NULL,`cumsum` int(11) NOT NULL,`start` int(11) NOT NULL,`right_key` int(11) NOT NULL,PRIMARY KEY (`rid`),KEY `parent` (`parent`),KEY `start` (`start`)) --INSERT INTO flatindex (rid,lvl) SELECT id,level FROM regions -- "" -- innerCnt - . -- fullCnt "" --repeat until affected_rows=0 UPDATE flatindex as fl1,(SELECT fl1.rid,sum(fl2.fullCnt)+fl1.innerCnt+1 as cnt FROM flatindex as fl1 INNER JOIN flatindex as fl2 ON fl2.parent=fl1.rid GROUP BY fl1.rid) as gr SET fl1.fullCnt=gr.cnt WHERE fl1.rid=gr.rid -- " " -- cumsum "" UPDATE flatindex as fl1, (SELECT SUM(fl2.fullCnt)+COUNT(*) +1 as fc,fl1.rid as rid from flatindex as fl1 LEFT JOIN flatindex as fl2 ON fl2.parent=fl1.parent WHERE fl2.rid<fl1.rid GROUP BY fl1.rid)as gr SET fl1.cumsum=gr.fc WHERE gr.rid=fl1.rid -- "" -- UPDATE flatindex SET start=cumsum+1 WHERE parent=0; -- repeat until affected_rows=0 UPDATE flatindex as fl,(SELECT start,rid FROM flatindex)as gr SET fl.start=gr.start+1 WHERE fl.prev=0 and fl.parent=gr.rid; UPDATE flatindex as fl,(SELECT start,parent FROM flatindex WHERE prev=0)as gr SET fl.start=cumsum+gr.start WHERE prev!=0 and fl.parent=gr.parent; -- "" -- UPDATE flatindex SET right_key = start+fullCnt+1; Option 2:
Let's transform our tree into a matpath, sort through strnatsort and hang some auto_incriment on this order. The numeric curve is ready. It remains only to find your neighbor (for example, on the right), and use its “number” as the right border.
In both cases, insertion and deletion is O (n), and sometimes O (1).
NS is just two numbers, the interval between the "buns" which is hidden all the most delicious. In the general case, the curve does not have to consist of integers; moreover, it fits perfectly on fractions. We take the already mentioned Stern - Brokaw and obtain the Koch curve.
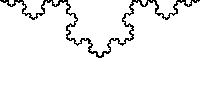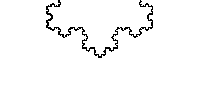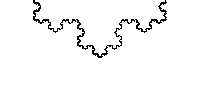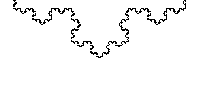
I hope you have read to this point, understand what the nested intervals are, it remains to understand why they are so good.
Imagine that you have a list of all hotels at the Hotellook (Aviasales). Imagine that you have a binding of these hotels in the country-region-city-district. The task is to find all hotels in Orekhovo-Borisovo South (narrow selection), all 5 star hotels in Turkey (large selection), and all hotels in a square 100 meters away from you.
Solution 1:
WHERE hotels_to_regions_ns.id between ns.left and ns.right Solution of situation 2:
WHERE hotels_to_regions_ns.id between ns.left and ns.right That's the secret - there is no difference . And in both cases it works quickly.
Solving situation 3 implies some kind of coordinate search . But in ordinary databases, this is a very complicated and expensive operation — a double-key search, or a 2D (spatial) key is simply difficult, expensive, and many reads are generated from different places of the disk. Well, simply because the order of data storage on disk 1D.
But the solution to the situation remains almost the same:
WHERE hotels_to_mortoncode.z between ns.zleft and ns.zright Where we use Morton, it's Z-curve code for converting 2D coordinates to 1D curve (this was written on Habré a couple of times), and then save it in Gray codes (two bits per division) and we can make quick samples along the pyramid ( Hello ObjectManager ).
For many, it is not entirely clear why the samples are fast - you should probably explain. Morton codes, besides being “addressing by quadtree”, have another property - codes for objects that are close by will be near.
preserving maps of the data points
Z is not the best solution, but it is great for quick samples of groups (tiles) of objects. Z-codes "hold" the locality of the data, including for objects of one node, the codes will be generally the same, or their variability will be clamped between the left and right values of the NS element.
Plus - NS, as I said before - some materialization of skip-sheets, a numerical curve or even B-trees. Technically, there is no difference. So, when you store data in NS, you store it in B-tree ... then ... wait ...
 |  |
In general, Z , Hilbert , GeoHash (Z codes in base64) and the company are the same
These codes are often used in various GIS systems, including Bing called their quad-code and uses for addressing tiles, and all this works without problems in 3D and in 4D space.
By reducing puzzles in a simple numeric curve.
And in the standard NestedSet.

The effect is always the same - everything starts working .
Here and the fairy tale is over, and who listened - well done.
PS: With you there were kashey and esosedi, who have been using NS and Z codes for sampling objects on the map for almost 7 years. Among which are HotelLook hotels (which are special.habrahabr.ru/aviasales ).
PPS: Join the Fourier series - convergence! Equality! Hilbert space!
PPPS: And don't forget the wisdom of the ages!
Source: https://habr.com/ru/post/251871/
All Articles