Fractal Flame - Build Algorithm

Fractal flame (or fractal sparks, English. Fractal flame) - an algorithm proposed by Scott Draves (Scott Draves) and using a system of iterated functions (CIF) for imaging. Due to the different values ​​of the seed for the pseudo-random number generator, you can get a variety of different "pictures". Although the fractality in them is far from always visible, the results are very interesting.

Under the cut - a brief description of the main points of the implementation of the algorithm.

To begin with, as in conventional CIFs, we will need to know the coefficients for each affine transformation of the plane (there may be several; each next will make its own “strokes” on the picture, as well as change the contribution of the previous ones). In matrix form, this transformation is as follows:
')


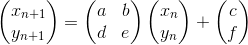
It is necessary to choose such coefficients so that the resulting transformation is compressive, that is, such that its scaling factor is less than one. There should be several of these transformations, and if you randomly choose one of them, in order to calculate the new coordinates of the point and display it on the screen, we will get an attractor - a set of points that the image will consist of.

Using a pseudo-random number sensor, it’s easy to get these coefficients. At the same time, it is necessary to check 3 conditions:





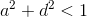
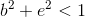
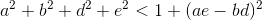
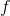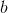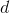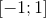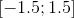All this refers to the coefficients that define the linear transformation. The remaining two and , perform translation - moving a point some distance. It is desirable that , , and were on the segment or . For and This is not necessary, but you should not set a too large segment, otherwise the image will be sparse.

In addition, along with each set of coefficients, you need to save the starting values ​​of the three color components of the RGB model, which will be assigned to the pixel that was hit for the first time. This is also done using a random number sensor and does not pose any special difficulties.

Now you need to decide what image of resolution you want to receive and prepare an array of pixels, each element of which will store:

• x and y coordinates;
• R, G and B values;
• number of hits.

The following are some non-linear transformations that will be performed on the x and y values ​​obtained after performing one of the affine transformations:

1. Sinusoidal: , ;
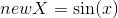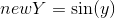2. Spherical: , ;
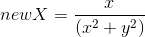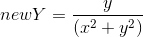3. Polar: , ;
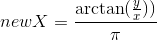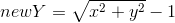4. A heart: , ;
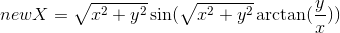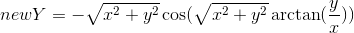5. Disk: , ;

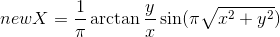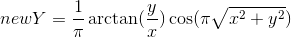At the end of the article - examples of images obtained using these and some other transformations, and further - pseudo-code rendering procedure:

void render(int n, int eqCount, int it, int xRes, int yRes) {  eqCount     ; for(int num=0; num<n; num++) { //   19201080  // XMIN=-1.777,XMAX=1.777,YMIN=-1,YMAX=1 //              newX=Rand(XMIN,XMAX); newY=Rand(YMIN,YMAX); // 20    , ..     for(int step=-20; step<it; step++) { //     i=Rand(0,eqCount); //   x=coeff[i].a*newX+coeff[i].b*newY+coeff[i].c; y=coeff[i].d*newX+coeff[i].e*newY+coeff[i].f;   ; if(step>=0 && newX∈[XMIN,XMAX] && newY∈[YMIN,YMAX]) { //  ,     x1=xRes-Trunc(((XMAX-newX)/(XMAX-XMIN))*xRes); y1=yRes-Trunc(((YMAX-newY)/(YMAX-YMIN))*yRes); //      if(x1<xRes && y1<yRes) { // ,       if(pixels[x1][y1].counter==0) { //   ,        pixels[x1][y1].red=coeff[i].red; pixels[x1][y1].green=coeff[i].green; pixels[x1][y1].blue=coeffs[i].blue; } else { //    ,  : pixels[x1][y1].red=(pixels[x1][y1].red+coeff[i].red)/2; pixels[x1][y1].green=(pixels[x1][y1].green+coeff[i].green)/2; pixels[x1][y1].blue=(pixels[x1][y1].blue+coeff[i].blue)/2; } //     pixels[x1][y1].counter++; } } } } } 

So, now you can display our image, but the result in this case will be too noisy, since the brightness of all pixels is the same. To fix this, it is necessary to conduct a logarithmic and gamma correction, reflecting the number of hits at each point with the help of brightness. Below is the code that performs the correction:

 void correction(int xRes, int yRes) { max=0.0; gamma=2.2; for (int row=0; row<xRes; row++) for (int col=0; col<yRes; col++) if (pixels[row][col].counter != 0) { pixels[row][col].normal=log10(pixels[row][col].counter); if (pixels[row][col].normal>max) max = pixels[row][col].normal; } for (int row=0; row<xRes; row++) for (int col=0; col<yRes; col++) { pixels[row][col].normal/=max; pixels[row][col].red =pixels[row][col].red*pow(pixels[row][col].normal,(1.0 / gamma)); pixels[row][col].green =pixels[row][col].green*pow(pixels[row][col].normal,(1.0 / gamma)); pixels[row][col].blue =pixels[row][col].blue*pow(pixels[row][col].normal,(1.0 / gamma)); } } 

Source

The implementation of the algorithm from James McCarthy in the C language is here , and the article by Scott Draves on the basis of which the algorithm was created is here .