Data compression methods
My supervisor and I are preparing a small monograph on image processing. I decided to submit to the habrasoobshchestva court a chapter on image compression algorithms. Since it is difficult to fit an entire chapter within one post, I decided to split it into three posts:
1. Data compression methods;
2. Image compression without loss;
3. Compression of lossy images.
Below you can see the first post of the series.
At the moment there are a large number of lossless compression algorithms, which can be divided into two large groups:
1. Flow and vocabulary algorithms. Algorithms of the RLE (run-length encoding), LZ *, etc. families belong to this group. A feature of all algorithms of this group is that the encoding does not use information about the frequencies of the symbols in the message, but information about sequences that were encountered earlier.
2. Algorithms of statistical (entropy) compression. This group of algorithms compresses information using the uneven frequencies with which various symbols are encountered in a message. The algorithms of this group include algorithms of arithmetic and prefix coding (using Shannon-Fanno, Huffman, intercept trees).
In a separate group, you can select information conversion algorithms. The algorithms of this group do not directly compress information, but their use greatly simplifies further compression using flow, vocabulary and entropy algorithms.
Run-Length Encoding (RLE) coding is one of the simplest and most common data compression algorithms. In this algorithm, a sequence of repeating characters is replaced by a character and the number of its repetitions.
For example, the string “AAAAA”, which requires 5 bytes to be stored (provided that a single byte is reserved for storing one character), can be replaced by “5A” consisting of two bytes. Obviously, the more effective this algorithm is, the longer the series of repetitions.
The main disadvantage of this algorithm is its extremely low efficiency on sequences of non-repeating characters. For example, if we consider the sequence “ABABAB” (6 bytes), then after applying the RLE algorithm, it will turn into “111111” (12 bytes). There are various methods to solve the problem of non-repeating characters.
')
The simplest method is the following modification: a byte encoding the number of repetitions should store information not only about the number of repetitions, but also about their presence. If the first bit is 1, then the next 7 bits indicate the number of repetitions of the corresponding character, and if the first bit is 0, then the next 7 bits indicate the number of characters to be taken without repeating. If you encode "ABABAB" using this modification, we get "-6ABABAB" (7 bytes). Obviously, the proposed method can significantly improve the efficiency of the RLE algorithm on non-repeating sequences of characters. The implementation of the proposed approach is shown in Listing 1:
Decoding a compressed message is very simple and comes down to a single pass through the compressed message, see Listing 2:
The second method of increasing the efficiency of the RLE algorithm is the use of information conversion algorithms that do not directly compress the data, but lead them to a form more convenient for compression. As an example of such an algorithm, we consider the BWT permutation, named after the inventors of the Burrows-Wheeler transform. This permutation does not change the characters themselves, but changes only their order in the string, while repeating substrings after applying the permutation are assembled into dense groups, which are much better compressed using the RLE algorithm. A direct BWT conversion is reduced to a sequence of the following steps:
1. Adding to the source line a special character for the line end, which is not found anywhere else;
2. Getting all cyclic permutations of the source line;
3. Sort received lines in lexicographical order;
4. Return the last column of the resulting matrix.
The implementation of this algorithm is shown in Listing 3.
The easiest way to explain this conversion is with a specific example. Take the line "ANANAS" and agree that the symbol of the end of the line will be the symbol "|" All cyclic permutations of this line and the result of their lexicographic sorting are given in Table. one.
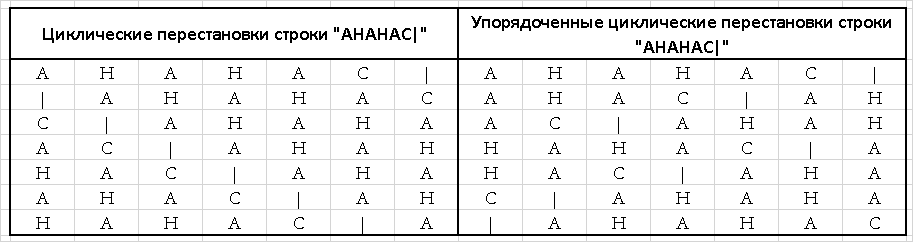
Those. the result of the direct conversion will be the string "| NNAAAC". It is easy to notice that this string is much better than the original one, compressed by the RLE algorithm, since there are long subsequences of repeated letters in it.
A similar effect can be achieved with the help of other transformations, but the advantage of the BWT transformation is that it is reversible, although the inverse transformation is more complicated than the direct one. In order to restore the original string, you must perform the following steps:
Create an empty matrix of size n * n, where n is the number of characters in the encoded message;
Fill the rightmost empty column with a coded message;
Sort table rows in lexicographical order;
Repeat steps 2-3 until there are empty columns;
Return the line that ends with the end of line character.
At first glance, the implementation of the inverse transform is not difficult, and one of the implementation options is shown in Listing 4.
But in practice, efficiency depends on the sorting algorithm chosen. Trivial algorithms with quadratic complexity obviously have a very negative effect on speed, therefore it is recommended to use efficient algorithms.
After sorting the table obtained in the seventh step, it is necessary to select from the table a row ending with a “|” character. It is easy to see that this string is the only one. So we looked at the BWT transform using a specific example.
Summarizing, we can say that the main advantage of a group of RLE algorithms is simplicity and speed of operation (including the speed of decoding), and the main disadvantage is inefficiency on non-repetitive character sets. The use of special permutations increases the efficiency of the algorithm, but also greatly increases the running time (especially decoding).
Group vocabulary algorithms, in contrast to the algorithms of the group RLE, encodes not the number of repetitions of characters, but the previously encountered sequences of characters. During the operation of the algorithms under consideration, a table is dynamically created with a list of already encountered sequences and their corresponding codes. This table is often called a dictionary, and the corresponding group of algorithms is called dictionary.
The following describes the simplest version of the dictionary algorithm:
Initialize the dictionary with all characters occurring in the input string;
Find the longest sequence (S) in the dictionary that matches the beginning of the message to be encoded;
Issue the code of the found sequence and delete it from the beginning of the encoded message;
If the end of the message is not reached, read the next © symbol and add Sc to the dictionary, go to step 2. Otherwise, exit.
For example, the just-initialized dictionary for the phrase “KUKUSHKAKUKUKONKUKUPILAKAPUSHON” is given in Table. 3:
In the process of compression, the dictionary will be supplemented by sequences encountered in the message. The process of replenishing the dictionary is given in Table. four.
In the description of the algorithm, the description of the situation was intentionally omitted when the dictionary is full. Depending on the variant of the algorithm, different behavior is possible: complete or partial cleaning of the dictionary, stopping the filling of the dictionary or expanding the dictionary with a corresponding increase in the code capacity. Each of these approaches has certain disadvantages. For example, stopping the replenishment of a dictionary can lead to a situation where the dictionary stores sequences that occur at the beginning of a compressible string, but are not encountered later. At the same time, cleaning the dictionary can lead to the removal of frequent sequences. Most implementations used when filling in the dictionary begin to track the degree of compression, and when it is lowered below a certain level, the dictionary is rebuilt. Next will be considered the simplest implementation, stopping the replenishment of the dictionary when it is filled.
To begin with, we define a dictionary as a record that stores not only the substrings encountered, but also the number of substrings stored in the dictionary:
Previously encountered subsequences are stored in the Words array, and their code is the number of subsequences in this array.
We will also define dictionary search and dictionary functions:
Using these functions, the coding process according to the described algorithm can be implemented as follows:
The result of coding will be the numbers of words in the dictionary.
The decoding process is reduced to the direct decoding of codes, while there is no need to transfer the created dictionary, it is enough that during decoding the dictionary is initialized in the same way as when encoding. Then the dictionary will be fully restored directly in the decoding process by concatenating the previous subsequence and the current character.
The only problem is possible in the following situation: when it is necessary to decode a subsequence that is not yet in the dictionary. It is easy to make sure that this is possible only when it is necessary to extract a substring that should be added at the current step. This means that the substring satisfies the cSc pattern, i.e. begins and ends with the same symbol. In this case, cS is a substring added in the previous step. The considered situation is the only one when it is necessary to decode a line that has not yet been added. Given the above, we can offer the following decoding option for a compressed string:
The advantages of vocabulary algorithms are their greater compared to RLE compression efficiency. Nevertheless, it should be understood that the actual use of these algorithms is associated with some implementation difficulties.
The Shannon-Fano algorithm is one of the first developed compression algorithms. The algorithm is based on the idea of representing more frequent symbols using shorter codes. In this case, codes obtained using the Shannon-Fano algorithm have the property of prefixity: i.e. no code is the beginning of any other code. The prefix property ensures that the encoding is one-to-one. The algorithm for constructing Shannon-Fano codes is presented below:
1. To break the alphabet into two parts, the total probabilities of the characters in which are as close as possible to each other.
2. In the prefix code of the first part of the characters add 0, in the prefix code of the second part of the characters add 1.
3. For each part (in which at least two characters) recursively perform steps 1-3.
Despite the comparative simplicity, the Shannon-Fano algorithm is not without flaws, the most significant of which is non-optimal coding. Although the split at each step is optimal, the algorithm does not guarantee an optimal result as a whole. Consider, for example, the following line: "AAAABVGDEZH." The corresponding Shannon-Fano tree and codes derived from it are shown in Fig. one:
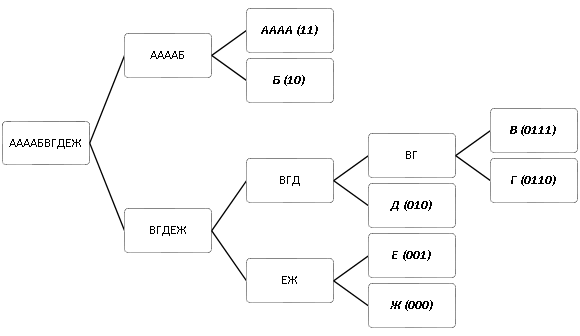
Without encoding, the message will occupy 40 bits (provided that each character is encoded with 4 bits), and using the Shannon-Fano algorithm, 4 * 2 + 2 + 4 + 4 + 3 + 3 + 3 = 27 bits. The message volume has decreased by 32.5%, but below it will be shown that this result can be significantly improved.
The Huffman coding algorithm, developed a few years after the Shannon-Fano algorithm, also has the property of prefixity, and, in addition, the proven minimal redundancy, this is precisely due to its extremely wide distribution. To obtain the Huffman codes, use the following algorithm:
1. All symbols of the alphabet are represented as free nodes, with the weight of the node being proportional to the frequency of the symbol in the message;
2. From the set of free nodes, two nodes are selected with a minimum weight and a new (parent) node is created with a weight equal to the sum of the weights of the selected nodes;
3. The selected nodes are removed from the free list, and the parent node created on the basis of them is added to this list;
4. Steps 2-3 are repeated as long as there are more than one node in the free list;
5. Based on the constructed tree, each character of the alphabet is assigned a prefix code;
6. The message is encoded by the received codes.
Consider the same example as in the case of the Shannon-Fano algorithm. The Huffman tree and codes received for the message “AAAABVGDEZH” are shown in Fig. 2:
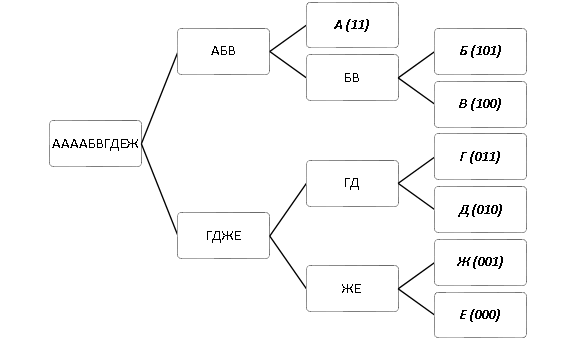
It is easy to calculate that the volume of the coded message will be 26 bits, which is less than in the Shannon-Fano algorithm. Separately, it is worth noting that, in view of the popularity of the Huffman algorithm, there are currently many options for Huffman coding, including adaptive coding, which does not require the transmission of symbol frequencies.
Among the shortcomings of the Huffman algorithm, a significant part of the problems associated with the complexity of implementation. The use of real variables to store the frequency of symbols of symbols is associated with a loss of accuracy, therefore, in practice, integer variables are often used, but, since the weight of the parent nodes is constantly growing, sooner or later an overflow occurs. Thus, despite the simplicity of the algorithm, its correct implementation can still cause some difficulties, especially for large alphabets.
Encoding with the help of intersecting functions - an algorithm developed by the authors that allows to obtain prefix codes. The algorithm is based on the idea of building a tree, each node of which contains a cutting function. To describe the algorithm in more detail, you need to enter several definitions.
A word is an ordered sequence of m bits (the number m is called the word depth).
Literal secant - a pair of discharge-value discharge type. For example, the literal (4,1) means that the 4 bits of the word must be equal to 1. If the condition of the literal is satisfied, then the literal is considered true, otherwise it is considered false.
A k-bit secant is a set of k literals. If all literals are true, then the secant function itself is true, otherwise it is false.
The tree is built so that each knot divides the alphabet into as close as possible parts. In Fig. 3 shows an example of a secant tree:
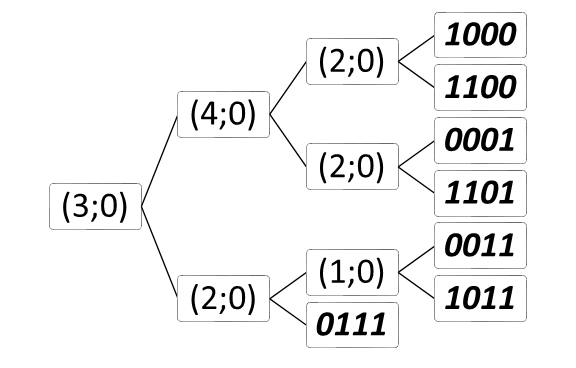
The tree of secant functions in the general case does not guarantee optimal coding, but it does provide extremely high speed of operation due to the simplicity of the operation in the nodes.
Arithmetic coding is one of the most effective ways to compress information. Unlike the Huffman algorithm, arithmetic coding allows encoding messages with entropy less than 1 bit per character. Since Most arithmetic coding algorithms are protected by patents, only the main ideas will be described below.
Suppose that in the alphabet used N characters a_1, ..., a_N, with frequencies p_1, ..., p_N, respectively. Then the algorithm of arithmetic coding will look as follows:
For the working half-interval, take [0; 1);
Split the working interval into N disjoint semi-intervals. The length of the i-th half-interval is proportional to p_i.
If the end of the message is not reached, select the i-th half-interval as the new working interval and go to step 2. Otherwise, return any number from the half-interval. Writing this number in binary code will be a coded message.
In Fig. 4 shows the encoding process of the message "ABAAV"
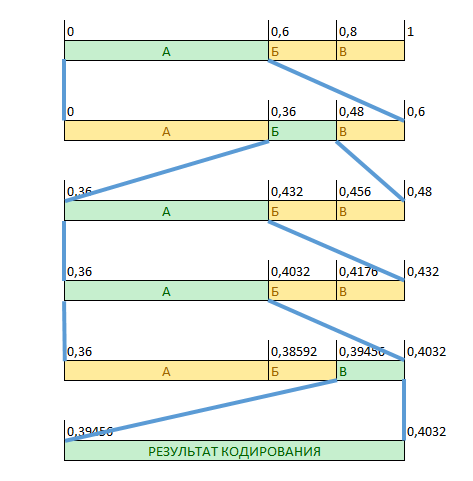
When decoding, it is necessary to perform a similar sequence of actions, only at each step it is necessary to additionally determine which particular character was encoded.
The obvious advantage of arithmetic coding is its efficiency, and the main (with the exception of patent restrictions) minus is the extremely high complexity of the coding and decoding processes.
1. Data compression methods;
2. Image compression without loss;
3. Compression of lossy images.
Below you can see the first post of the series.
At the moment there are a large number of lossless compression algorithms, which can be divided into two large groups:
1. Flow and vocabulary algorithms. Algorithms of the RLE (run-length encoding), LZ *, etc. families belong to this group. A feature of all algorithms of this group is that the encoding does not use information about the frequencies of the symbols in the message, but information about sequences that were encountered earlier.
2. Algorithms of statistical (entropy) compression. This group of algorithms compresses information using the uneven frequencies with which various symbols are encountered in a message. The algorithms of this group include algorithms of arithmetic and prefix coding (using Shannon-Fanno, Huffman, intercept trees).
In a separate group, you can select information conversion algorithms. The algorithms of this group do not directly compress information, but their use greatly simplifies further compression using flow, vocabulary and entropy algorithms.
Flow and vocabulary algorithms
Series Length Coding
Run-Length Encoding (RLE) coding is one of the simplest and most common data compression algorithms. In this algorithm, a sequence of repeating characters is replaced by a character and the number of its repetitions.
For example, the string “AAAAA”, which requires 5 bytes to be stored (provided that a single byte is reserved for storing one character), can be replaced by “5A” consisting of two bytes. Obviously, the more effective this algorithm is, the longer the series of repetitions.
The main disadvantage of this algorithm is its extremely low efficiency on sequences of non-repeating characters. For example, if we consider the sequence “ABABAB” (6 bytes), then after applying the RLE algorithm, it will turn into “111111” (12 bytes). There are various methods to solve the problem of non-repeating characters.
')
The simplest method is the following modification: a byte encoding the number of repetitions should store information not only about the number of repetitions, but also about their presence. If the first bit is 1, then the next 7 bits indicate the number of repetitions of the corresponding character, and if the first bit is 0, then the next 7 bits indicate the number of characters to be taken without repeating. If you encode "ABABAB" using this modification, we get "-6ABABAB" (7 bytes). Obviously, the proposed method can significantly improve the efficiency of the RLE algorithm on non-repeating sequences of characters. The implementation of the proposed approach is shown in Listing 1:
- type
- TRLEEncodedString = array of byte ;
- function RLEEncode ( InMsg : ShortString ) : TRLEEncodedString ;
- var
- MatchFl : boolean ;
- MatchCount : shortint ;
- EncodedString : TRLEEncodedString ;
- N , i : byte ;
- begin
- N : = 0 ;
- SetLength ( EncodedString , 2 * length ( InMsg ) ) ;
- while length ( InMsg ) > = 1 do
- begin
- MatchFl : = ( length ( InMsg ) > 1 ) and ( InMsg [ 1 ] = InMsg [ 2 ] ) ;
- MatchCount : = 1 ;
- while ( MatchCount < = 126 ) and ( MatchCount <length ( InMsg ) ) and ( ( InMsg [ MatchCount ] = InMsg [ MatchCount + 1 ] ) = MatchFl ) do
- MatchCount : = MatchCount + 1 ;
- if MatchFl then
- begin
- N : = N + 2 ;
- EncodedString [ N - 2 ] : = MatchCount + 128 ;
- EncodedString [ N - 1 ] : = ord ( InMsg [ 1 ] ) ;
- end
- else
- begin
- if MatchCount <> length ( InMsg ) then
- MatchCount : = MatchCount - 1 ;
- N : = N + 1 + MatchCount ;
- EncodedString [ N - 1 - MatchCount ] : = - MatchCount + 128 ;
- for i : = 1 to MatchCount do
- EncodedString [ N - 1 - MatchCount + i ] : = ord ( InMsg [ i ] ) ;
- end ;
- delete ( InMsg , 1 , MatchCount ) ;
- end ;
- SetLength ( EncodedString , N ) ;
- RLEEncode : = EncodedString ;
- end ;
Decoding a compressed message is very simple and comes down to a single pass through the compressed message, see Listing 2:
- type
- TRLEEncodedString = array of byte ;
- function RLEDecode ( InMsg : TRLEEncodedString ) : ShortString ;
- var
- RepeatCount : shortint ;
- i , j : word ;
- OutMsg : ShortString ;
- begin
- OutMsg : = '' ;
- i : = 0 ;
- while i <length ( InMsg ) do
- begin
- RepeatCount : = InMsg [ i ] - 128 ;
- i : = i + 1 ;
- if RepeatCount < 0 then
- begin
- RepeatCount : = abs ( RepeatCount ) ;
- for j : = i to i + RepeatCount - 1 do
- OutMsg : = OutMsg + chr ( InMsg [ j ] ) ;
- i : = i + RepeatCount ;
- end
- else
- begin
- for j : = 1 to RepeatCount do
- OutMsg : = OutMsg + chr ( InMsg [ i ] ) ;
- i : = i + 1 ;
- end ;
- end ;
- RLEDecode : = OutMsg ;
- end ;
The second method of increasing the efficiency of the RLE algorithm is the use of information conversion algorithms that do not directly compress the data, but lead them to a form more convenient for compression. As an example of such an algorithm, we consider the BWT permutation, named after the inventors of the Burrows-Wheeler transform. This permutation does not change the characters themselves, but changes only their order in the string, while repeating substrings after applying the permutation are assembled into dense groups, which are much better compressed using the RLE algorithm. A direct BWT conversion is reduced to a sequence of the following steps:
1. Adding to the source line a special character for the line end, which is not found anywhere else;
2. Getting all cyclic permutations of the source line;
3. Sort received lines in lexicographical order;
4. Return the last column of the resulting matrix.
The implementation of this algorithm is shown in Listing 3.
- const
- EOMsg = '|' ;
- function BWTEncode ( InMsg : ShortString ) : ShortString ;
- var
- OutMsg : ShortString ;
- ShiftTable : array of ShortString ;
- LastChar : ANSIChar ;
- N , i : word ;
- begin
- InMsg : = InMsg + EOMsg ;
- N : = length ( InMsg ) ;
- SetLength ( ShiftTable , N + 1 ) ;
- ShiftTable [ 1 ] : = InMsg ;
- for i : = 2 to N do
- begin
- LastChar : = InMsg [ N ] ;
- InMsg : = LastChar + copy ( InMsg , 1 , N - 1 ) ;
- ShiftTable [ i ] : = InMsg ;
- end ;
- Sort ( ShiftTable ) ;
- OutMsg : = '' ;
- for i : = 1 to N do
- OutMsg : = OutMsg + ShiftTable [ i ] [ N ] ;
- BWTEncode : = OutMsg ;
- end ;
The easiest way to explain this conversion is with a specific example. Take the line "ANANAS" and agree that the symbol of the end of the line will be the symbol "|" All cyclic permutations of this line and the result of their lexicographic sorting are given in Table. one.

Those. the result of the direct conversion will be the string "| NNAAAC". It is easy to notice that this string is much better than the original one, compressed by the RLE algorithm, since there are long subsequences of repeated letters in it.
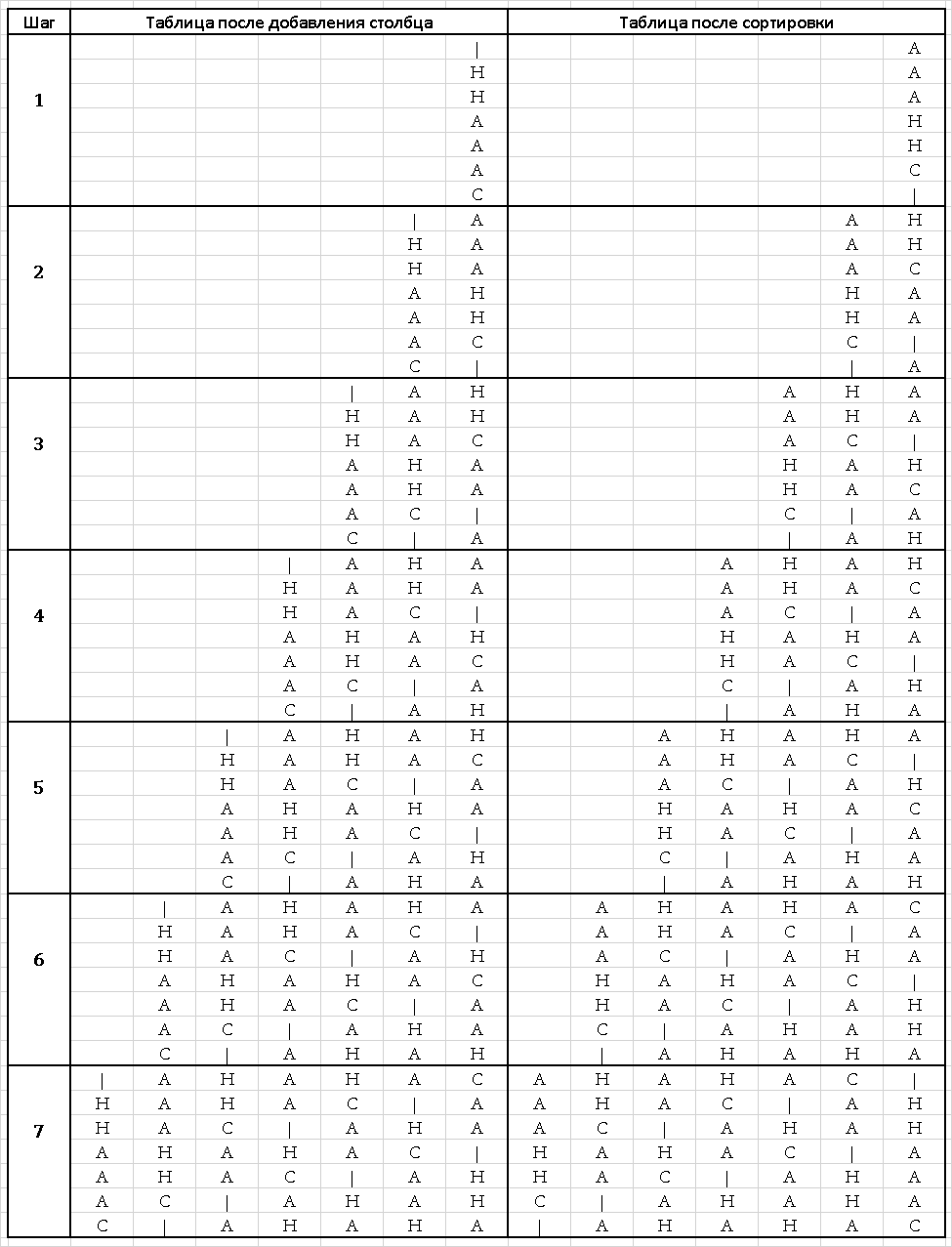
A similar effect can be achieved with the help of other transformations, but the advantage of the BWT transformation is that it is reversible, although the inverse transformation is more complicated than the direct one. In order to restore the original string, you must perform the following steps:
Create an empty matrix of size n * n, where n is the number of characters in the encoded message;
Fill the rightmost empty column with a coded message;
Sort table rows in lexicographical order;
Repeat steps 2-3 until there are empty columns;
Return the line that ends with the end of line character.
At first glance, the implementation of the inverse transform is not difficult, and one of the implementation options is shown in Listing 4.
- const
- EOMsg = '|' ;
- function BWTDecode ( InMsg : ShortString ) : ShortString ;
- var
- OutMsg : ShortString ;
- ShiftTable : array of ShortString ;
- N , i , j : word ;
- begin
- OutMsg : = '' ;
- N : = length ( InMsg ) ;
- SetLength ( ShiftTable , N + 1 ) ;
- for i : = 0 to N do
- ShiftTable [ i ] : = '' ;
- for i : = 1 to N do
- begin
- for j : = 1 to N do
- ShiftTable [ j ] : = InMsg [ j ] + ShiftTable [ j ] ;
- Sort ( ShiftTable ) ;
- end ;
- for i : = 1 to N do
- if ShiftTable [ i ] [ N ] = EOMsg then
- OutMsg : = ShiftTable [ i ] ;
- delete ( OutMsg , N , 1 ) ;
- BWTDecode : = OutMsg ;
- end ;
But in practice, efficiency depends on the sorting algorithm chosen. Trivial algorithms with quadratic complexity obviously have a very negative effect on speed, therefore it is recommended to use efficient algorithms.

After sorting the table obtained in the seventh step, it is necessary to select from the table a row ending with a “|” character. It is easy to see that this string is the only one. So we looked at the BWT transform using a specific example.
Summarizing, we can say that the main advantage of a group of RLE algorithms is simplicity and speed of operation (including the speed of decoding), and the main disadvantage is inefficiency on non-repetitive character sets. The use of special permutations increases the efficiency of the algorithm, but also greatly increases the running time (especially decoding).
Dictionary compression (LZ algorithms)
Group vocabulary algorithms, in contrast to the algorithms of the group RLE, encodes not the number of repetitions of characters, but the previously encountered sequences of characters. During the operation of the algorithms under consideration, a table is dynamically created with a list of already encountered sequences and their corresponding codes. This table is often called a dictionary, and the corresponding group of algorithms is called dictionary.
The following describes the simplest version of the dictionary algorithm:
Initialize the dictionary with all characters occurring in the input string;
Find the longest sequence (S) in the dictionary that matches the beginning of the message to be encoded;
Issue the code of the found sequence and delete it from the beginning of the encoded message;
If the end of the message is not reached, read the next © symbol and add Sc to the dictionary, go to step 2. Otherwise, exit.
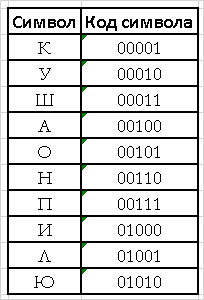
For example, the just-initialized dictionary for the phrase “KUKUSHKAKUKUKONKUKUPILAKAPUSHON” is given in Table. 3:

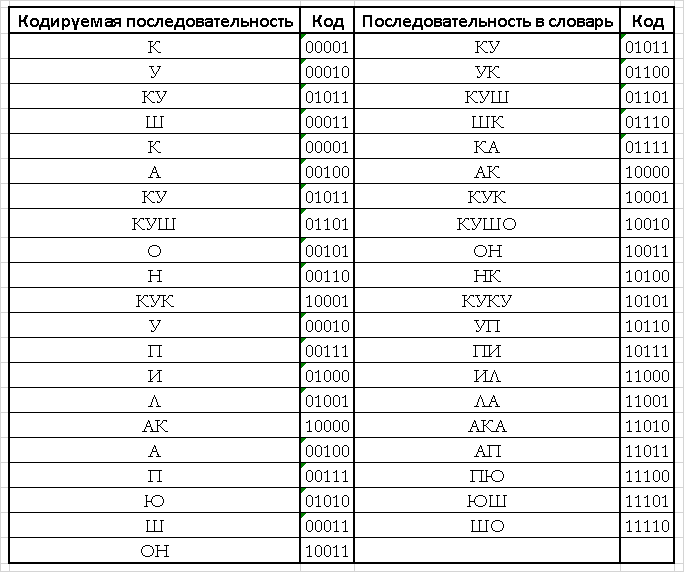
In the process of compression, the dictionary will be supplemented by sequences encountered in the message. The process of replenishing the dictionary is given in Table. four.

In the description of the algorithm, the description of the situation was intentionally omitted when the dictionary is full. Depending on the variant of the algorithm, different behavior is possible: complete or partial cleaning of the dictionary, stopping the filling of the dictionary or expanding the dictionary with a corresponding increase in the code capacity. Each of these approaches has certain disadvantages. For example, stopping the replenishment of a dictionary can lead to a situation where the dictionary stores sequences that occur at the beginning of a compressible string, but are not encountered later. At the same time, cleaning the dictionary can lead to the removal of frequent sequences. Most implementations used when filling in the dictionary begin to track the degree of compression, and when it is lowered below a certain level, the dictionary is rebuilt. Next will be considered the simplest implementation, stopping the replenishment of the dictionary when it is filled.
To begin with, we define a dictionary as a record that stores not only the substrings encountered, but also the number of substrings stored in the dictionary:
- type
- TDictionary = record
- WordCount : byte ;
- Words : array of string ;
- end ;
Previously encountered subsequences are stored in the Words array, and their code is the number of subsequences in this array.
We will also define dictionary search and dictionary functions:
- const
- MAX_DICT_LENGTH = 256 ;
- function FindInDict ( D : TDictionary ; str : ShortString ) : integer ;
- var
- r : integer ;
- i : integer ;
- fl : boolean ;
- begin
- r : = - 1 ;
- if d . WordCount > 0 then
- begin
- i : = D. WordCount ;
- fl : = false ;
- while ( not fl ) and ( i> = 0 ) do
- begin
- i : = i - 1 ;
- fl : = D. Words [ i ] = str ;
- end ;
- end ;
- if fl then
- r : = i ;
- FindInDict : = r ;
- end ;
- procedure AddToDict ( var D : TDictionary ; str : ShortString ) ;
- begin
- if d . WordCount <MAX_DICT_LENGTH then
- begin
- D. WordCount : = D. WordCount + 1 ;
- SetLength ( D. Words , D. WordCount ) ;
- D. Words [ D. WordCount - 1 ] : = str ;
- end ;
- end ;
Using these functions, the coding process according to the described algorithm can be implemented as follows:
- function LZWEncode ( InMsg : ShortString ) : TEncodedString ;
- var
- OutMsg : TEncodedString ;
- tmpstr : ShortString ;
- D : TDictionary ;
- i , N : byte ;
- begin
- SetLength ( OutMsg , length ( InMsg ) ) ;
- N : = 0 ;
- InitDict ( D ) ;
- while length ( InMsg ) > 0 do
- begin
- tmpstr : = InMsg [ 1 ] ;
- while ( FindInDict ( D , tmpstr ) > = 0 ) and ( length ( InMsg ) > length ( tmpstr ) ) do
- tmpstr : = tmpstr + InMsg [ length ( tmpstr ) + 1 ] ;
- if FindInDict ( D , tmpstr ) < 0 then
- delete ( tmpstr , length ( tmpstr ) , 1 ) ;
- OutMsg [ N ] : = FindInDict ( D , tmpstr ) ;
- N : = N + 1 ;
- delete ( InMsg , 1 , length ( tmpstr ) ) ;
- if length ( InMsg ) > 0 then
- AddToDict ( D , tmpstr + InMsg [ 1 ] ) ;
- end ;
- SetLength ( OutMsg , N ) ;
- LZWEncode : = OutMsg ;
- end ;
The result of coding will be the numbers of words in the dictionary.
The decoding process is reduced to the direct decoding of codes, while there is no need to transfer the created dictionary, it is enough that during decoding the dictionary is initialized in the same way as when encoding. Then the dictionary will be fully restored directly in the decoding process by concatenating the previous subsequence and the current character.
The only problem is possible in the following situation: when it is necessary to decode a subsequence that is not yet in the dictionary. It is easy to make sure that this is possible only when it is necessary to extract a substring that should be added at the current step. This means that the substring satisfies the cSc pattern, i.e. begins and ends with the same symbol. In this case, cS is a substring added in the previous step. The considered situation is the only one when it is necessary to decode a line that has not yet been added. Given the above, we can offer the following decoding option for a compressed string:
- function LZWDecode ( InMsg : TEncodedString ) : ShortString ;
- var
- D : TDictionary ;
- OutMsg , tmpstr : ShortString ;
- i : byte ;
- begin
- OutMsg : = '' ;
- tmpstr : = '' ;
- InitDict ( D ) ;
- for i : = 0 to length ( InMsg ) - 1 do
- begin
- if InMsg [ i ] > = D. WordCount then
- tmpstr : = D. Words [ InMsg [ i - 1 ] ] + D. Words [ InMsg [ i - 1 ] ] [ 1 ]
- else
- tmpstr : = D. Words [ InMsg [ i ] ] ;
- OutMsg : = OutMsg + tmpstr ;
- if i> 0 then
- AddToDict ( D , D. Words [ InMsg [ i - 1 ] ] + tmpstr [ 1 ] ) ;
- end ;
- LZWDecode : = OutMsg ;
- end ;
The advantages of vocabulary algorithms are their greater compared to RLE compression efficiency. Nevertheless, it should be understood that the actual use of these algorithms is associated with some implementation difficulties.
Entropy coding
Encoding with Shannon-Fano trees
The Shannon-Fano algorithm is one of the first developed compression algorithms. The algorithm is based on the idea of representing more frequent symbols using shorter codes. In this case, codes obtained using the Shannon-Fano algorithm have the property of prefixity: i.e. no code is the beginning of any other code. The prefix property ensures that the encoding is one-to-one. The algorithm for constructing Shannon-Fano codes is presented below:
1. To break the alphabet into two parts, the total probabilities of the characters in which are as close as possible to each other.
2. In the prefix code of the first part of the characters add 0, in the prefix code of the second part of the characters add 1.
3. For each part (in which at least two characters) recursively perform steps 1-3.
Despite the comparative simplicity, the Shannon-Fano algorithm is not without flaws, the most significant of which is non-optimal coding. Although the split at each step is optimal, the algorithm does not guarantee an optimal result as a whole. Consider, for example, the following line: "AAAABVGDEZH." The corresponding Shannon-Fano tree and codes derived from it are shown in Fig. one:

Without encoding, the message will occupy 40 bits (provided that each character is encoded with 4 bits), and using the Shannon-Fano algorithm, 4 * 2 + 2 + 4 + 4 + 3 + 3 + 3 = 27 bits. The message volume has decreased by 32.5%, but below it will be shown that this result can be significantly improved.
Huffman Tree Coding
The Huffman coding algorithm, developed a few years after the Shannon-Fano algorithm, also has the property of prefixity, and, in addition, the proven minimal redundancy, this is precisely due to its extremely wide distribution. To obtain the Huffman codes, use the following algorithm:
1. All symbols of the alphabet are represented as free nodes, with the weight of the node being proportional to the frequency of the symbol in the message;
2. From the set of free nodes, two nodes are selected with a minimum weight and a new (parent) node is created with a weight equal to the sum of the weights of the selected nodes;
3. The selected nodes are removed from the free list, and the parent node created on the basis of them is added to this list;
4. Steps 2-3 are repeated as long as there are more than one node in the free list;
5. Based on the constructed tree, each character of the alphabet is assigned a prefix code;
6. The message is encoded by the received codes.
Consider the same example as in the case of the Shannon-Fano algorithm. The Huffman tree and codes received for the message “AAAABVGDEZH” are shown in Fig. 2:

It is easy to calculate that the volume of the coded message will be 26 bits, which is less than in the Shannon-Fano algorithm. Separately, it is worth noting that, in view of the popularity of the Huffman algorithm, there are currently many options for Huffman coding, including adaptive coding, which does not require the transmission of symbol frequencies.
Among the shortcomings of the Huffman algorithm, a significant part of the problems associated with the complexity of implementation. The use of real variables to store the frequency of symbols of symbols is associated with a loss of accuracy, therefore, in practice, integer variables are often used, but, since the weight of the parent nodes is constantly growing, sooner or later an overflow occurs. Thus, despite the simplicity of the algorithm, its correct implementation can still cause some difficulties, especially for large alphabets.
Coding with the help of trees
Encoding with the help of intersecting functions - an algorithm developed by the authors that allows to obtain prefix codes. The algorithm is based on the idea of building a tree, each node of which contains a cutting function. To describe the algorithm in more detail, you need to enter several definitions.
A word is an ordered sequence of m bits (the number m is called the word depth).
Literal secant - a pair of discharge-value discharge type. For example, the literal (4,1) means that the 4 bits of the word must be equal to 1. If the condition of the literal is satisfied, then the literal is considered true, otherwise it is considered false.
A k-bit secant is a set of k literals. If all literals are true, then the secant function itself is true, otherwise it is false.
The tree is built so that each knot divides the alphabet into as close as possible parts. In Fig. 3 shows an example of a secant tree:

The tree of secant functions in the general case does not guarantee optimal coding, but it does provide extremely high speed of operation due to the simplicity of the operation in the nodes.
Arithmetic coding
Arithmetic coding is one of the most effective ways to compress information. Unlike the Huffman algorithm, arithmetic coding allows encoding messages with entropy less than 1 bit per character. Since Most arithmetic coding algorithms are protected by patents, only the main ideas will be described below.
Suppose that in the alphabet used N characters a_1, ..., a_N, with frequencies p_1, ..., p_N, respectively. Then the algorithm of arithmetic coding will look as follows:
For the working half-interval, take [0; 1);
Split the working interval into N disjoint semi-intervals. The length of the i-th half-interval is proportional to p_i.
If the end of the message is not reached, select the i-th half-interval as the new working interval and go to step 2. Otherwise, return any number from the half-interval. Writing this number in binary code will be a coded message.
In Fig. 4 shows the encoding process of the message "ABAAV"

When decoding, it is necessary to perform a similar sequence of actions, only at each step it is necessary to additionally determine which particular character was encoded.
The obvious advantage of arithmetic coding is its efficiency, and the main (with the exception of patent restrictions) minus is the extremely high complexity of the coding and decoding processes.
Source: https://habr.com/ru/post/251295/
All Articles