Quantum sandbox: part 1
What is a quantum state? What is the usual state different from the quantum state? At what point does the usual state become quantum, and what will happen if quantumness is taken away from it? Will it still be quantum or will it become ordinary? It has just been quantum. Probably, it became confusing, and the cat also became confused.

In this article we will try to answer these questions and understand the essence of quantum mechanics.
The goal: to write a simple program that “simulates” quantum evolution, so that you can finally touch these qubits with handles.

Table of contents:

• Part I: The Classic State
• Part II: The Quantum State
• Part III: Cat
• Part IV: Swarm

What is the usual "state"? This term is used so often that it began to be perceived completely intuitively.
')

Part I: The Classic State

Question number 1: "Given a particle P, which can be observed along the segment . What is the state of a P particle?
Answer: The classical state of a particle P is a number from a segment. .

An attentive reader will be attracted by the word "observe" - ​​how is this generally understood?
It turned out that all this time on the site 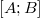some "detectors" were located that "observed", but why didn't we say anything about them? And how many pieces are there?

We said that the state of a particle is a number from a segment 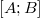. Power set 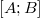equal to the continuum - between our “borders” A and B there are infinitely many numbers, and they are located infinitely close to each other - means we need infinitely many detectors for each point? Sounds pretty expensive, right?

But, asserting that a state is a number, we, it turns out, mean exactly that. Exactly what we have in stock infinitely many detectors. But this is not so. And this can not be in principle.

In practice, we would break the segment into a finite number of segments, and in the intersections we would place detectors, and each detector would be able to approximately tell whether there is a particle in its vicinity or not.



What was done above is called quantization . In this case, we quantized the segment into segments. Quantum is an indivisible portion of something within the framework of the model used, an abstract term.

The most interesting phenomena begin precisely because the state of the particle has now ceased to be just a number.

Part II: The Quantum State

Question number 2: "Given a particle P, which can be observed only in the vicinity of a certain number of detectors in the segment . What is the state of a P particle?
Answer: ???

Consider an example:

Dan segment 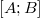and two detectors located at points A and B.

Each detector shows a certain number, according to which we can determine how far the particle is from this detector.

A is the first detector 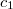- his testimony ( 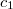= 1, if the particle got directly to A)
B - the second detector 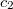- his testimony ( 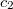= 1 if the particle got directly to C)

Let us make an assumption about a particle in order to somehow limit the scope of our research:

Assumption: A particle is one, it cannot just take and clone itself.

From this assumption it follows that if a particle is in A, then it cannot be in B, and vice versa.



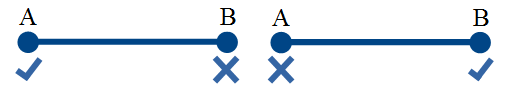
Or, which is the same if 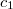= 1, then 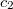= 0 and vice versa.



Now consider the “motion” of a particle from detector A to detector B. The particle was in A ( 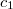= 1, 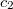= 0), then it began to fly toward B. The readings of detector A began to decrease ( 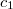<1), and detector B’s readings began to increase ( 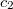> 0). Then the particle reached detector B and its readings are equal 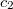= 1, and detector A notifies us that there are no particles in it 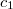= 0

Thus, we describe the state of a particle with the help of the detectors themselves and their readings.



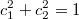
This entry means that configuration X includes detector A, showing us the number c1, and detector B, showing us the number c2.

Question number 2: "Given a particle P, which can be observed only in the vicinity of the detectors located at points A and B, which are the quantization of the segment on one segment . What is the state of a P particle?
Assumption: A particle is one, it cannot take and just clone itself.
Answer: The quantum state of a particle P is a vector of two-dimensional Hilbert space. with basis vectors A = {1, 0} and B = {0, 1}. Moreover, this vector is normalized to one ( ), and the basis vectors A and B are the classical states from question 1. Such particles are also called qubits due to the two-dimensionality of the basis. When the basis is three-dimensional, the particles are called quatrites , etc.

Question number 2 (generalized): “Given a particle P, which can only be observed in the vicinity of a finite number of detectors located at points which are segment quantization on N - 1 segment . What is the state of a P particle?
Assumption: A particle is one, it cannot take and just clone itself.
Answer: The quantum state of a particle P is a vector of N-dimensional Hilbert space with basis vectors . Moreover, this vector is normalized to unity. , and basis vectors are the classic states from question 1.

Part III: Cat

We have come close to the most interesting manifestations of quantum mechanics. Without a doubt, every reader has heard a little about such terms as “quantum superposition” or “quantum entanglement” - these effects and other similar magic begin at the very moment when you will not make those conclusions that are not required .

We have two definitions of a condition.

Definition # 1: The classical state of a particle P is a number from a segment ...
Assumption: A particle is one, it cannot take and just clone itself.
Definition # 2 : The quantum state of a particle P is the vector of a two-dimensional Hilbert space ...

Usually, conclusions are derived from some definitions, but here we will be interested in what does not follow from the definition, but we still call it consequences for harmony.

Corollary # 1: It does not follow from the definition of a quantum state that a particle is at one point in a segment. In general, nowhere does not follow.

That is, the particle can be located at two points at once! For example for a particle that is in a quantum state. 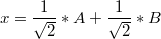it does not follow that it is at one point. Yes, maybe it is somewhere in the middle, at some point M between A and B, but by asserting something like that, we will manifest an unreasonable liberty.

Corollary №2: It does not follow from the definition of a quantum state that the particle is divided into small pieces, some pieces have flown there, and others have flown there.

How is this generally understood? How can a particle be at two points at once and still remain indivisible ? We are used to the fact that the Schrödinger cat is alive and dead at the same time, which means that the particle is also here and there at the same time. But she is indivisible . Did she stretch out?

We introduce the concept of a swarm and an instance of virtual particles.

Part IV: Swarm

Definition # 3: A particle instance is a virtual object that corresponds to a position in space at a given time, a motion trajectory over time, and a complex number (called amplitude) that has a module and an argument for which all algebraic rules are true:
Definition number 4: Swarm - a collection of copies.
Definition No. 5: Particle is a swarm (when performing a quantization operation of space).

Imagine an instance as a ball, inside which there is an arrow corresponding to a complex number in the complex plane. It is important to understand that the ball can have one direction of movement , and the arrow inside it - another , that is, these directions are different .



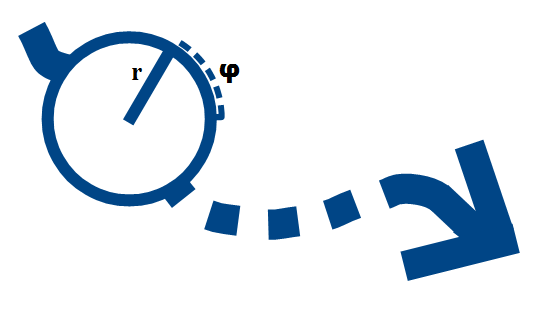
But why different? The fact is that the processes inside an elementary particle are so difficult to describe that the influence of these processes on the movement of the particle itself is impossible to predict at a fundamental level, therefore the connection between the arrow inside the ball and the direction of motion of the ball itself does not exist for us.


The verbal manipulations that we have just accomplished are useless unless the laws of variation of the values ​​of r , φ and the law of motion are determined, because everything rests on them.

The law of variation of the argument: φ constantly increases uniformly by the value of dφ as the instance moves.

In other words, our integrated shooters are constantly turning in the same direction. Why do you need it? So that the system under no circumstances ceases to evolve.

The law of addition and multiplication: As you move along a single trajectory, the amplitudes multiply. Amplitudes along various trajectories are added.

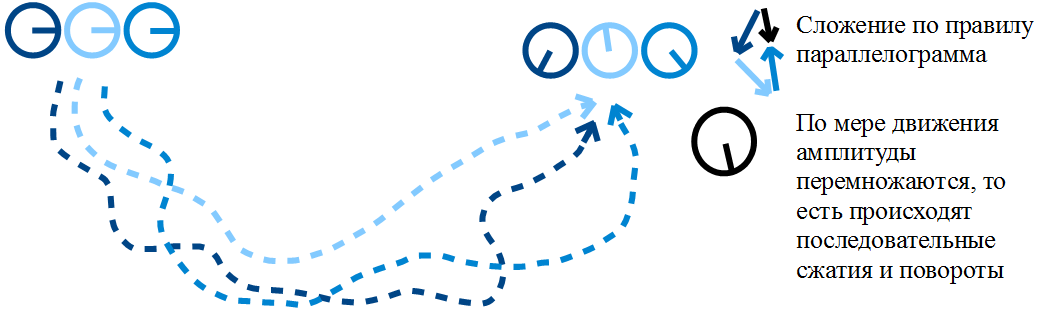
This law is also known as the principle of superposition in quantum mechanics.

The law of motion of copies in space: Let a particle be given in a quantum state. An instance is given that is located in some cell of space (on which a quantization operation on cells was performed). There are neighboring cells around this space cell.

1. This instance clones itself as many times as there are neighboring points around it.
2. Each clone moves to the neighboring point that corresponds to it.
3. This father instance is moving to an arbitrary point.

The process is repeated for each instance.

1. Inside each ball is the same complex arrow, which rotates at an angle dφ after each movement of the specimen from one cell to another.

2. So we have a huge dynamic system that constantly clones itself.

3. The direction of movement of the very first specimen, in general, determines the movements of the swarm, but the swarm nevertheless extends in all directions. If you track the movement of any individual specimen (not paying attention to the clones), then it will move along an absolutely random trajectory.

We do not forget that inside each ball there is a complex arrow, which has its own direction and length . How to predict which resultant arrow will be in an arbitrary space cell at a given time? Obviously, for this you need to know what happened to the entire system at the previous time. We obtain a differential equation (it is called the Schrödinger equation in honor of Schrödinger, who discovered it).

The law of movement of copies in space: Let - the quantum state of a particle, a column vector in which amplitudes are recorded one by one in all cells of space. - energy operator, which determines the way of interaction between the instances. Then the swarm moves according to the following law: .

The formation of the energy operator "piece by piece handles" will be discussed in the next article.



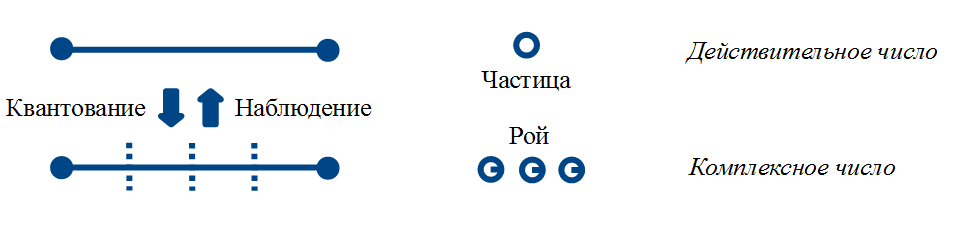
Constructively, we understand the following concepts:

1. The classical state of a particle as a number (and not like anything else)
2. The quantum state of a particle as a vector (and not as “what is in several places at once”)
3. Particle as a swarm (when performing a quantization operation)
4. The principle of superposition of the swarm , according to which amplitudes multiply along one trajectory, and add along all possible trajectories
5. Law of movement of copies

In the next article we will look at the most interesting - systems with an arbitrary number of particles. Let us examine what the tensors, entangled states are, and finally, we write a program capable of “simulating” the quantum evolution and conveniently drawing it.

Since the topic of quantum mechanics has been actively popularized recently (starting from the relevant journals, ending with entire exhibitions devoted to “quantum entanglement”), it seems to me that there is a need to monitor the current state so that you can go in and check “what about us quanta? "Perhaps this information will be useful - pleaded.ru