The mathematical problem of 100 boxes and the rescue of prisoners
I offer the readers of Habrahabr a translation of the publication “100 Prisoners Escape Puzzle” , which I found on the website of the DataGenetics company. All errors on this article, please send in private messages.
According to the condition of the task, there are 100 prisoners in the prison, each of whom has a personal number from 1 to 100. The jailer decides to give the prisoners a chance for release and offers to pass the test invented by them. If all the prisoners manage, they are free, if at least one fails, everyone will die.

The jailer goes to the secret room and prepares 100 boxes with lids. On each box he puts the numbers numbered from 1 to 100. Then he brings 100 paper plates, according to the number of prisoners, and numbers these plates from 1 to 100. After that, he shuffles 100 plates and places one box on each box, closing the lid . Prisoners do not see the jailer perform all these actions.
')

The competition begins, the jailer takes each prisoner one by one to the room with the boxes and tells the prisoner that they must find the box in which there will be a sign with the prisoner's number. Prisoners try to find a sign with their number by opening the boxes. Everyone is allowed to open up to 50 boxes; if each of the prisoners finds their number, then the prisoners will be released, if at least one of them does not find his number in 50 attempts, then all the prisoners will die.

In order for prisoners to be released, ALL prisoners must pass the test successfully.
So what is the chance that prisoners have mercy?
What is the optimal strategy for prisoners?
At first glance, this task seems almost hopeless. It seems that the chance for each prisoner to find his own plate is microscopically small. In addition, prisoners cannot exchange information with each other during the trial.
The odds of one prisoner are 50:50. Only 100 boxes and he can open up to 50 boxes in search of his nameplate. If he opens the boxes at random and opens half of all the boxes, he will find his plate in the open half of the boxes, or his plate will remain in the closed 50 boxes. His chances of success are ½.

Take two prisoners. If both choose boxes at random, for each of them the odds are ½, and for two ½x½ = ¼.
(for two prisoners, the success will be in one case out of four).
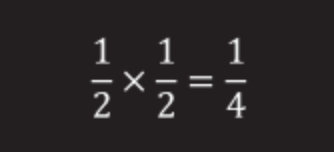
For three prisoners, the odds are ½ × ½ × ½ = ⅛.
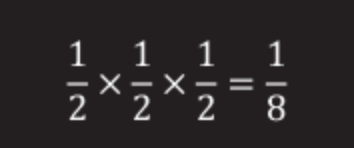
For 100 prisoners, the odds are as follows: ½ × ½ ×… ½ × ½ (multiplication 100 times).
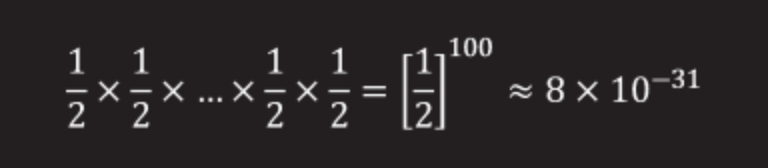
It equals
That is a very small chance. In this scenario, most likely, all prisoners will be dead.
It is recommended to ponder before reading the decision further.
If every prisoner opens the boxes at random, they are unlikely to pass the test. There is a strategy in which prisoners can count on success in more than 30% of cases. This is a stunningly incredible result (if you haven't heard about this math problem before).
More than 30% for all 100 prisoners! Yes, it is even more than the chances for two prisoners, provided that they open the boxes at random. But how is this possible?
It is clear that one in each prisoner the chances cannot be higher than 50% (there is no way for communication between prisoners). But do not forget that the information is stored in the location of the plates inside the boxes. No one mixes signs between individual prisoners' visits to the room, so we can use this information.
To begin with, I will tell the solution, then I will explain why it works.
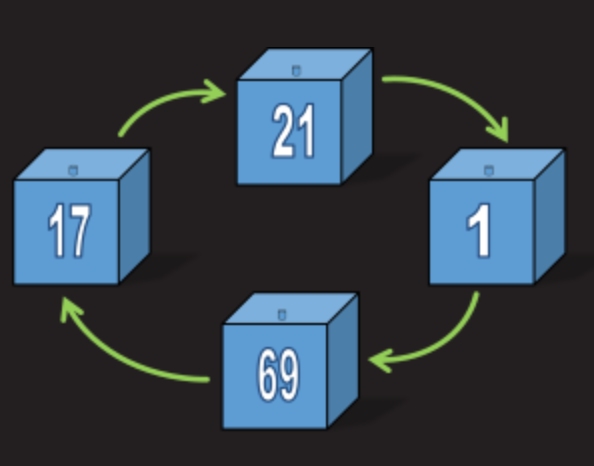
The strategy is extremely easy. The first prisoner opens the box with the number that is written on his clothes. For example, the prisoner number 78 opens the box with number 78. If he finds his number on the plate inside the box, then that's great! If not, he looks at the number on the plate in “his” box and then opens the next box with that number. Opening the second box, he looks at the number plate inside this box and opens the third box with this number. Then simply transfer this strategy to the remaining boxes. For clarity, look at the picture:
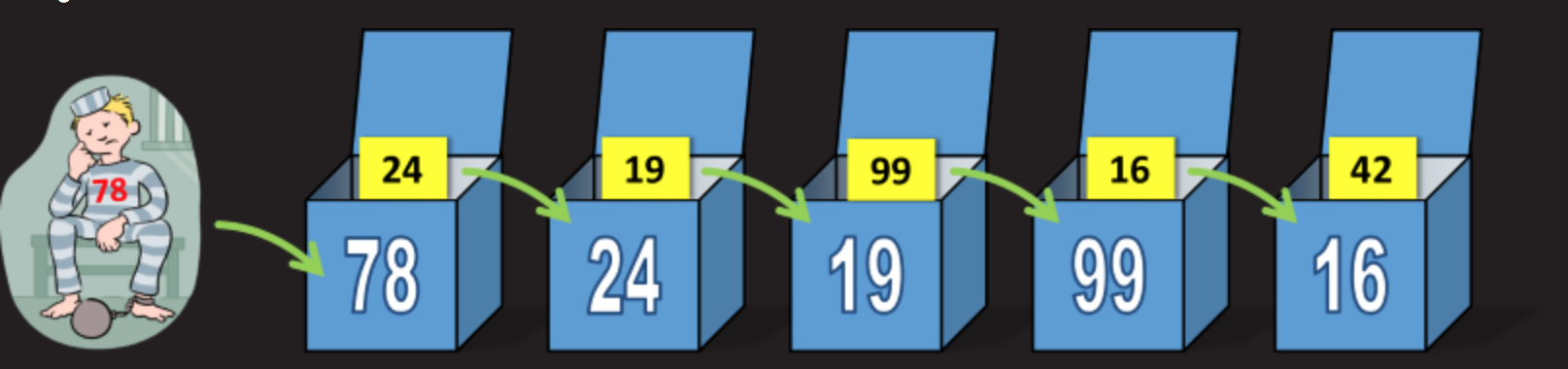
In the end, the prisoner will either find his number, or reach a limit of 50 boxes. At first glance, this seems pointless compared to a simple box selection at random (and this is the case for one individual prisoner), but since all 100 prisoners will use the same set of boxes, this makes sense.
There is one plate in each box - and this plate is unique. This means that the tablet is in the box with the same number, or it points to another box. Since all the plates are unique, then for each box there is only one tablet pointing to it (and just one way to get to this box).

If you think about it, the boxes form a closed circular chain. One box can be part of only one chain, since inside the box there is only one pointer to the next and, accordingly, in the previous box, only one pointer to this box (programmers can see the analogy with linked lists).
If the box does not point to itself (the box number is equal to the number of the plate in it), then it will be in the chain. Some chains may consist of two boxes, some longer.
Since all prisoners start with a box with the same number as on their clothes, they, by definition, fall on a chain that contains their nameplate (there is only one nameplate that points to this box).
Exploring the boxes along this chain in a circle, they are guaranteed to eventually find their nameplate.
The only question remains is whether they will find their plate in 50 moves.
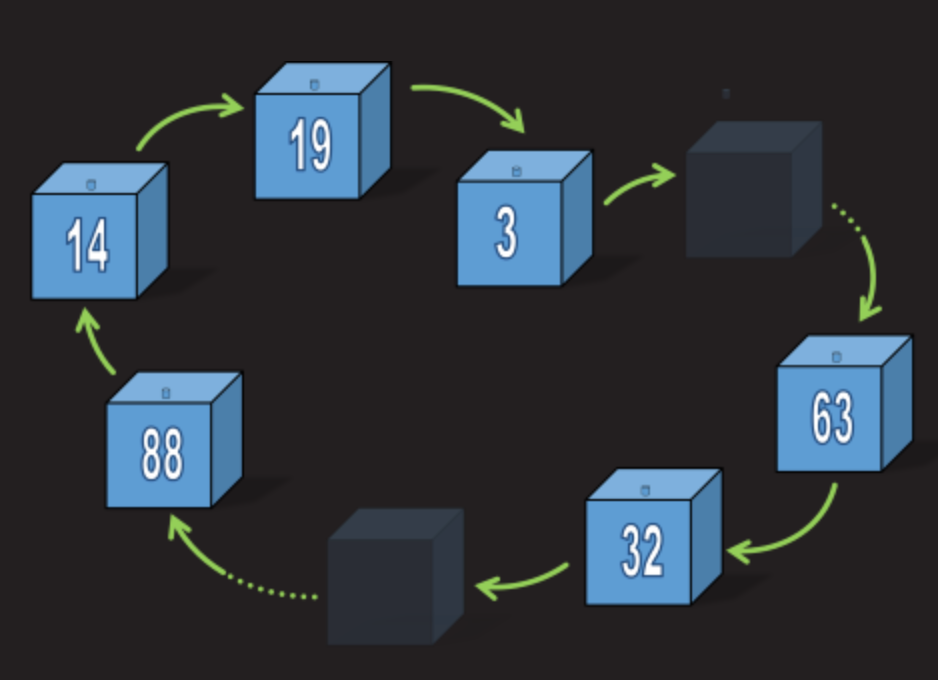
In order for all prisoners to pass the test, the maximum length of the chain must be less than 50 boxes. If the chain is longer than 50 boxes, prisoners with numbers from these chains will fail the test - and all prisoners will be dead.
Think about it for a second. It turns out that there can be only one chain that is longer than 50 boxes in any case of plates (we have only 100 boxes, so if one chain is longer than 50, the rest will be shorter than 50 in the end).

Once you have convinced yourself that to achieve success, the maximum chain length must be less than or equal to 50, and there can be only one long chain in any set, we can calculate the success rate of passing the test:

So, what do we need to figure out the probability of the existence of a long chain?
For a chain with a length l, the probability that the boxes will be outside this chain is equal to:
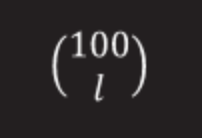
In this collection of numbers there is (l-1)! ways to arrange labels.
The remaining plates can be located (100-l)! ways (do not forget that the length of the chain does not exceed 50).
Given this, the number of permutations that contain a chain of exact length l: (> 50)

It turns out that there are 100 (!) Ways of plate layout, so the probability of the existence of a chain of length l is 1 / l. By the way, this result does not depend on the number of boxes.
As we already know, there can be only one option in which there is a chain of length> 50, so the probability of success is calculated using this formula:
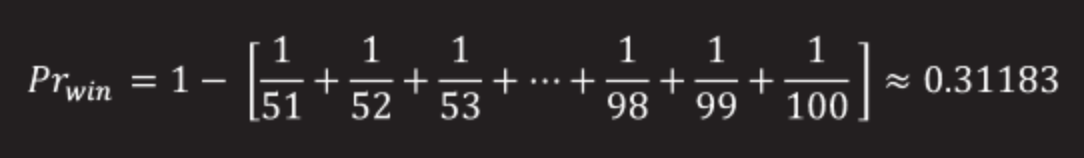
31.18% - the probability that the size of the longest chain will be less than 50 and each of the prisoners will be able to find his own plate, taking into account the limit of 50 attempts.
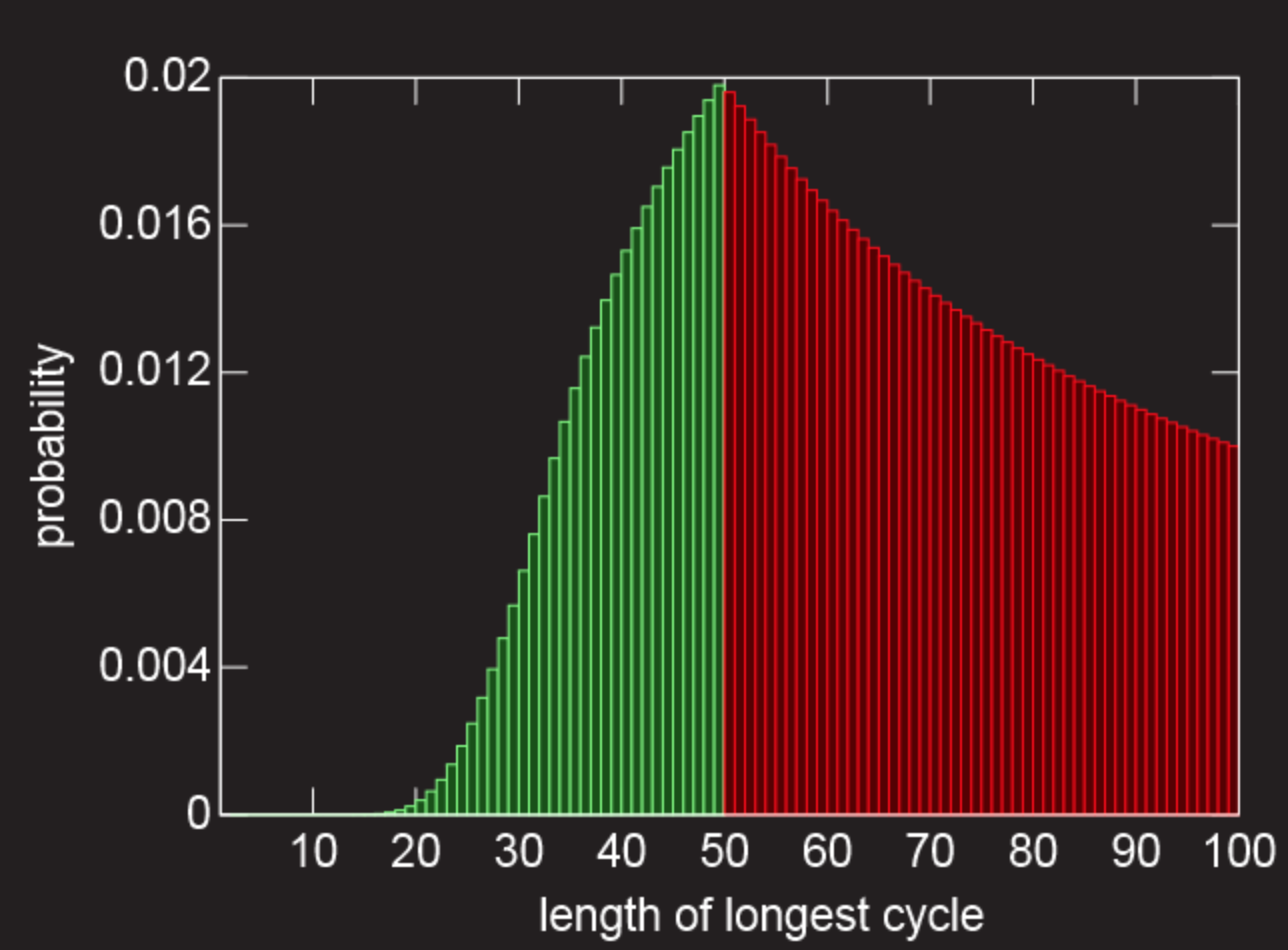
Below is a graph showing the probabilities (along the y-axis) for all chains of length l (on the x-axis). Red color means all “failures” (this curve here is just a 1 / l plot). Green color means “success” (the calculation is a little more difficult for this part of the graph, since there are several ways to determine the maximum length <50). The overall probability is made up of green columns at a 31.18% chance of escape.
In mathematics, the nth harmonic number is the sum of the reciprocals of the first n consecutive numbers of the natural series.

We can calculate the jailbreak probability by adding the corresponding harmonic numbers.
We calculate the limit if instead of 100a boxes we have an arbitrary large number of boxes (let's assume that we have 2n boxes in total).
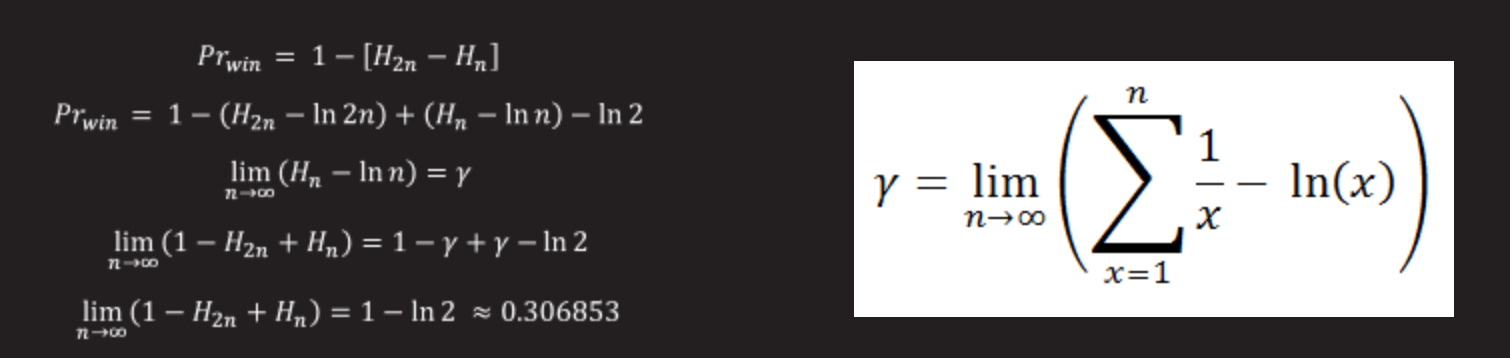
The Euler – Mascheroni constant is a constant defined as the limit of the difference between the partial sum of the harmonic series and the natural logarithm of a number.
(If you made a decision in which prisoners randomly guess boxes, then with an increase in the number of prisoners, the probability of salvation tends to zero!)
Does anyone else remember an additional question? What can our helpful comrade do to increase the chances of survival?
Now we already know the solution, so the strategy here is simple: he must study all the signs and find the longest chain of boxes. If the longest chain is less than 50, then it does not need to change the plates at all, or change them so that the longest chain does not become longer than 50. However, if he found a chain longer than 50 boxes, all he needs is to change the contents of the two boxes from this chain in order to break this chain into two shorter chains.
As a result of this strategy, there will be no long chains and all prisoners will be guaranteed to find their tablet and salvation. So, swapping the two tablets, we reduce the probability of salvation to 100%!
According to the condition of the task, there are 100 prisoners in the prison, each of whom has a personal number from 1 to 100. The jailer decides to give the prisoners a chance for release and offers to pass the test invented by them. If all the prisoners manage, they are free, if at least one fails, everyone will die.

Task
The jailer goes to the secret room and prepares 100 boxes with lids. On each box he puts the numbers numbered from 1 to 100. Then he brings 100 paper plates, according to the number of prisoners, and numbers these plates from 1 to 100. After that, he shuffles 100 plates and places one box on each box, closing the lid . Prisoners do not see the jailer perform all these actions.
')

The competition begins, the jailer takes each prisoner one by one to the room with the boxes and tells the prisoner that they must find the box in which there will be a sign with the prisoner's number. Prisoners try to find a sign with their number by opening the boxes. Everyone is allowed to open up to 50 boxes; if each of the prisoners finds their number, then the prisoners will be released, if at least one of them does not find his number in 50 attempts, then all the prisoners will die.

In order for prisoners to be released, ALL prisoners must pass the test successfully.
So what is the chance that prisoners have mercy?
- After the prisoner opens the box and checks the plate with it, it is placed back in the box and the lid is closed again;
- Places can not be changed;
- Prisoners cannot leave tips to each other or somehow interact with each other after starting the test;
- Prisoners are allowed to discuss the strategy before the test.
What is the optimal strategy for prisoners?
Additional question:
If a fellow prisoner (not a trial participant) will have the opportunity to enter the secret room before the test begins, examine all the plates in all the boxes and (optionally, but not necessarily) swap two plates from the two boxes (while the comrade will not have the opportunity to inform prisoners about the result of his actions, then what strategy should he take to increase the prisoners' chances of salvation?
Solution unlikely?
At first glance, this task seems almost hopeless. It seems that the chance for each prisoner to find his own plate is microscopically small. In addition, prisoners cannot exchange information with each other during the trial.
The odds of one prisoner are 50:50. Only 100 boxes and he can open up to 50 boxes in search of his nameplate. If he opens the boxes at random and opens half of all the boxes, he will find his plate in the open half of the boxes, or his plate will remain in the closed 50 boxes. His chances of success are ½.

Take two prisoners. If both choose boxes at random, for each of them the odds are ½, and for two ½x½ = ¼.
(for two prisoners, the success will be in one case out of four).
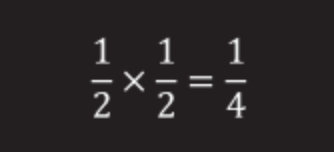
For three prisoners, the odds are ½ × ½ × ½ = ⅛.
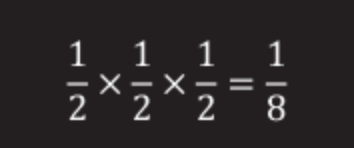
For 100 prisoners, the odds are as follows: ½ × ½ ×… ½ × ½ (multiplication 100 times).
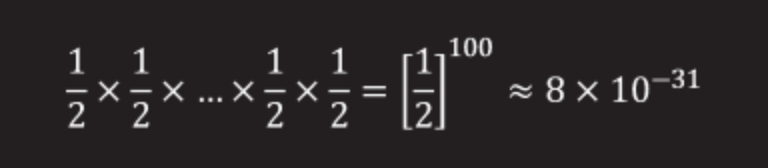
It equals
Pr ≈ 0.00000000000000000000000000008
That is a very small chance. In this scenario, most likely, all prisoners will be dead.
It is recommended to ponder before reading the decision further.
Incredible answer
If every prisoner opens the boxes at random, they are unlikely to pass the test. There is a strategy in which prisoners can count on success in more than 30% of cases. This is a stunningly incredible result (if you haven't heard about this math problem before).
More than 30% for all 100 prisoners! Yes, it is even more than the chances for two prisoners, provided that they open the boxes at random. But how is this possible?
It is clear that one in each prisoner the chances cannot be higher than 50% (there is no way for communication between prisoners). But do not forget that the information is stored in the location of the plates inside the boxes. No one mixes signs between individual prisoners' visits to the room, so we can use this information.
Decision
To begin with, I will tell the solution, then I will explain why it works.
The strategy is extremely easy. The first prisoner opens the box with the number that is written on his clothes. For example, the prisoner number 78 opens the box with number 78. If he finds his number on the plate inside the box, then that's great! If not, he looks at the number on the plate in “his” box and then opens the next box with that number. Opening the second box, he looks at the number plate inside this box and opens the third box with this number. Then simply transfer this strategy to the remaining boxes. For clarity, look at the picture:

In the end, the prisoner will either find his number, or reach a limit of 50 boxes. At first glance, this seems pointless compared to a simple box selection at random (and this is the case for one individual prisoner), but since all 100 prisoners will use the same set of boxes, this makes sense.
The beauty of this mathematical task is not only to know the result, but also to understand why this strategy works.
So why does the strategy work?
There is one plate in each box - and this plate is unique. This means that the tablet is in the box with the same number, or it points to another box. Since all the plates are unique, then for each box there is only one tablet pointing to it (and just one way to get to this box).

If you think about it, the boxes form a closed circular chain. One box can be part of only one chain, since inside the box there is only one pointer to the next and, accordingly, in the previous box, only one pointer to this box (programmers can see the analogy with linked lists).
If the box does not point to itself (the box number is equal to the number of the plate in it), then it will be in the chain. Some chains may consist of two boxes, some longer.

Since all prisoners start with a box with the same number as on their clothes, they, by definition, fall on a chain that contains their nameplate (there is only one nameplate that points to this box).
Exploring the boxes along this chain in a circle, they are guaranteed to eventually find their nameplate.
The only question remains is whether they will find their plate in 50 moves.

Chain length
In order for all prisoners to pass the test, the maximum length of the chain must be less than 50 boxes. If the chain is longer than 50 boxes, prisoners with numbers from these chains will fail the test - and all prisoners will be dead.
If the maximum length of the longest chain is less than 50 boxes, then all prisoners will pass the test!
Think about it for a second. It turns out that there can be only one chain that is longer than 50 boxes in any case of plates (we have only 100 boxes, so if one chain is longer than 50, the rest will be shorter than 50 in the end).

Chances of deal with a long chain
Once you have convinced yourself that to achieve success, the maximum chain length must be less than or equal to 50, and there can be only one long chain in any set, we can calculate the success rate of passing the test:

More math
So, what do we need to figure out the probability of the existence of a long chain?
For a chain with a length l, the probability that the boxes will be outside this chain is equal to:
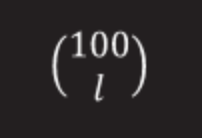
In this collection of numbers there is (l-1)! ways to arrange labels.
The remaining plates can be located (100-l)! ways (do not forget that the length of the chain does not exceed 50).
Given this, the number of permutations that contain a chain of exact length l: (> 50)

It turns out that there are 100 (!) Ways of plate layout, so the probability of the existence of a chain of length l is 1 / l. By the way, this result does not depend on the number of boxes.
As we already know, there can be only one option in which there is a chain of length> 50, so the probability of success is calculated using this formula:
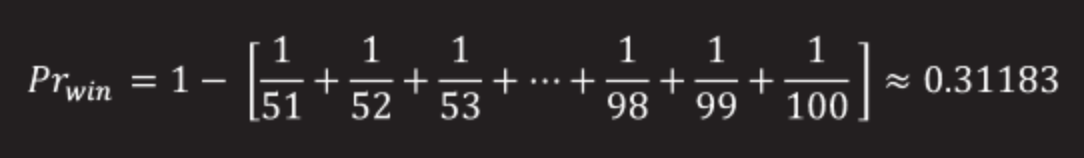
Result
31.18% - the probability that the size of the longest chain will be less than 50 and each of the prisoners will be able to find his own plate, taking into account the limit of 50 attempts.
The probability that all prisoners will find their tablets and pass the test of 31.18%
Below is a graph showing the probabilities (along the y-axis) for all chains of length l (on the x-axis). Red color means all “failures” (this curve here is just a 1 / l plot). Green color means “success” (the calculation is a little more difficult for this part of the graph, since there are several ways to determine the maximum length <50). The overall probability is made up of green columns at a 31.18% chance of escape.

Harmonic number (this part of the article for geeks)
In mathematics, the nth harmonic number is the sum of the reciprocals of the first n consecutive numbers of the natural series.

We can calculate the jailbreak probability by adding the corresponding harmonic numbers.
We calculate the limit if instead of 100a boxes we have an arbitrary large number of boxes (let's assume that we have 2n boxes in total).
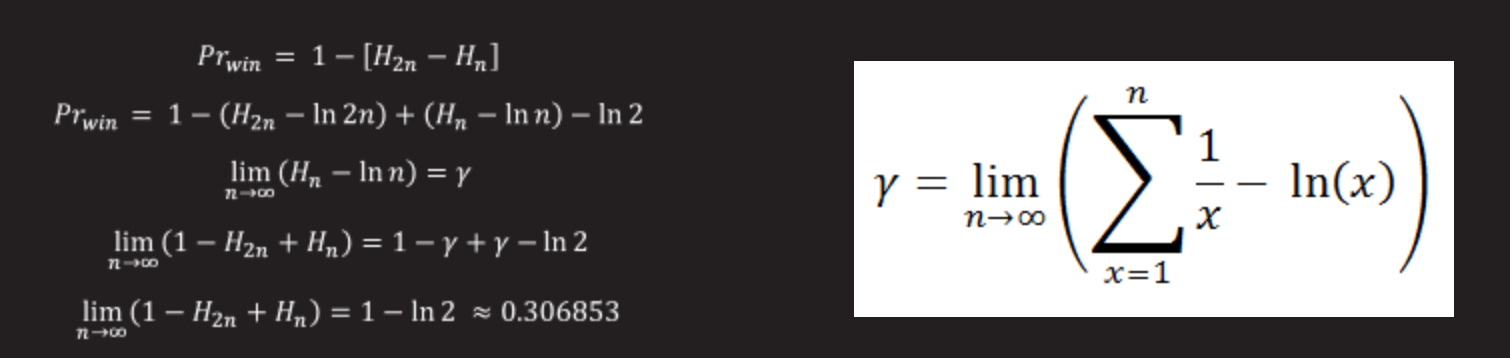
The Euler – Mascheroni constant is a constant defined as the limit of the difference between the partial sum of the harmonic series and the natural logarithm of a number.
As the number of prisoners increases, provided that the supervisor permits prisoners to open half of all the boxes, the chance for salvation tends to be 30.685%
(If you made a decision in which prisoners randomly guess boxes, then with an increase in the number of prisoners, the probability of salvation tends to zero!)
Additional question
Does anyone else remember an additional question? What can our helpful comrade do to increase the chances of survival?
Now we already know the solution, so the strategy here is simple: he must study all the signs and find the longest chain of boxes. If the longest chain is less than 50, then it does not need to change the plates at all, or change them so that the longest chain does not become longer than 50. However, if he found a chain longer than 50 boxes, all he needs is to change the contents of the two boxes from this chain in order to break this chain into two shorter chains.
As a result of this strategy, there will be no long chains and all prisoners will be guaranteed to find their tablet and salvation. So, swapping the two tablets, we reduce the probability of salvation to 100%!
Source: https://habr.com/ru/post/250817/
All Articles