Visual brute force on the example of solving a 3D puzzle
Once upon a time friends gave just such a puzzle:

I could not assemble it myself (there was always one fragment left). Therefore, it was decided to write a program.
')
For those who do not like to read, the solution is available by reference (attention, the processor is heavily loaded).
So, we have a puzzle consisting of 25 identical elements that need to be laid in a 5x5x5 cube, where the smallest edge of the element is taken as a unit of measurement.
The choice of language fell on JavaScript. Having sacrificed performance for the sake of visualization (I really wanted to make a visualized brute force, like in the movies), since the brute force process did not promise to be too long (why, it will be written below).
The main assembly process will occur in a three-dimensional integer array (5x5x5), let's call it “boxes”, where the non-negative value will be the cell occupied by the element cube. For more information, this value will be the ordinal position of the element in three-dimensional space. There are a total of 24 element positions in three-dimensional space, if the angle of rotation around each axis is a multiple of 90 °. For ease of counting the number of positions, I presented a Rubik's cube, whose faces are painted in different colors. Every time he addresses us with a new face and turns four times clockwise by 90 ° so that this face always looks at us. Total 6 faces x 4 turns = 24 positions in space where our eyes are fixed.
Knowing the number of positions of the object in three-dimensional space and supplementing it with a reflection of each state (the other two reflections both together and separately will give either the same cube or its first reflection after torsion), we get that for each unique solution of the puzzle there may be more than one , there are still 47 of its variations, and, consequently, the time required for the solution will be less than the time of complete enumeration. Unfortunately, I can’t bring the formula for calculating the number of moves to find a solution, so if anyone can, please write in the comments, add to the article.
The position of the element in space will be the relative coordinates of the five unit cubes that make up the element: the coordinates will be taken relative to the base point (its coordinates are [0,0,0], respectively). The main condition for the location of the base point is its obligatory location on the element in such a way that when this element is filled with a cube, the base point is located at the base level of the cube. Under the base level we mean the level along the Z axis, at which the assembly is currently taking place (the levels below are completely filled). Thus, we have simplified further calculations for ourselves (and not only).
The order of assembly is determined by the puzzle itself: we collect from the bottom up, as soon as the level is filled completely, we proceed to the next. The order of the brute force is determined by the array of the positions of the elements in space. If, after partially filling the level for some free point, it is impossible to find a position, the previous element found is considered incorrect, the box is removed from the current state array, and the search continues.
As for visualization, we will execute the three-dimensional representation of the cube in the form of five sections along the Z axis, along the slice for each level.
The sections are 5x5 tables, filled with cells with non-negative numbers from the “box”. The cells are additionally painted with different colors to separate the puzzle elements from each other. To reduce the load, the state of the array will be displayed once per second or at critical moments: start, pause, stop while finding the answer. In addition, we’ll use a “save string” to work with which you can pause, make changes to the code and continue the search from the pause rather than from the beginning. Also, we will display the number of cycles (for the moment of the end of the cycle we will take the moment of displaying the current state of the array), the number of “iterations” for the last cycle and the total number of “iterations”.
Of the features it is worth noting that in the prelaunch, at the beginning, an array of possible positions is created for each coordinate box, in order to cut off the positions that cannot be located at this point in advance. Also for versatility added the ability to change the size of the "box" in all three coordinates. To increase the rendering speed, added an array of cells in the slicing tables.
Full code with comments:
- github
- JSFiddle
We start, we wait (it took me 114 cycles on Google Chrome, going through 96969659 options), we look at the answer and collect it in real life.
UPD According to Serator's advice , added the possibility of using web workers, however, it is not possible to parallelize the calculations, since the following calculation depends on the results of the previous one, so the calculations themselves were made separately for the web worker, and the visualization was left in the main thread.
The results of the work are shown below in the tables *. The fraction indicates the calculation time with the calculation tab active / with the calculation tab inactive. All additions and extensions at the time of calculation were disabled.
Using web worker **:
Without a web worker:
* - The results of the work depend on the total load of the machine, so the tables show the averaged values. The measurement error was about 5%.
** - The result of the work is presented when sending values to the visualization every 50 thousand searches, for the remaining values the result fit into the error.
You can check it yourself by running the script on the local web server.
In fact, the process of the calculation itself did not parallelize, so the time spent on the calculation with the web worker took more than without it, however, its use may be useful for carrying out the calculation in the background (when the calculation tab is inactive). In addition, Firefox turned out to be the slowest for settling with a web worker, and is comparable in time when performing calculations without it. Separately, it is worth noting that thanks to the web worker, visualization can be redrawn more often, which looks much more beautiful than without it.

I could not assemble it myself (there was always one fragment left). Therefore, it was decided to write a program.
')
For those who do not like to read, the solution is available by reference (attention, the processor is heavily loaded).
So, we have a puzzle consisting of 25 identical elements that need to be laid in a 5x5x5 cube, where the smallest edge of the element is taken as a unit of measurement.
The choice of language fell on JavaScript. Having sacrificed performance for the sake of visualization (I really wanted to make a visualized brute force, like in the movies), since the brute force process did not promise to be too long (why, it will be written below).
We divide the puzzle elements into cubes with a single side.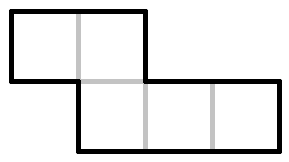

The main assembly process will occur in a three-dimensional integer array (5x5x5), let's call it “boxes”, where the non-negative value will be the cell occupied by the element cube. For more information, this value will be the ordinal position of the element in three-dimensional space. There are a total of 24 element positions in three-dimensional space, if the angle of rotation around each axis is a multiple of 90 °. For ease of counting the number of positions, I presented a Rubik's cube, whose faces are painted in different colors. Every time he addresses us with a new face and turns four times clockwise by 90 ° so that this face always looks at us. Total 6 faces x 4 turns = 24 positions in space where our eyes are fixed.
Knowing the number of positions of the object in three-dimensional space and supplementing it with a reflection of each state (the other two reflections both together and separately will give either the same cube or its first reflection after torsion), we get that for each unique solution of the puzzle there may be more than one , there are still 47 of its variations, and, consequently, the time required for the solution will be less than the time of complete enumeration. Unfortunately, I can’t bring the formula for calculating the number of moves to find a solution, so if anyone can, please write in the comments, add to the article.
The position of the element in space will be the relative coordinates of the five unit cubes that make up the element: the coordinates will be taken relative to the base point (its coordinates are [0,0,0], respectively). The main condition for the location of the base point is its obligatory location on the element in such a way that when this element is filled with a cube, the base point is located at the base level of the cube. Under the base level we mean the level along the Z axis, at which the assembly is currently taking place (the levels below are completely filled). Thus, we have simplified further calculations for ourselves (and not only).
24 positions
//x,y,z var elems=[ [[0,0,0],[1,0,0],[1,1,0],[2,1,0],[3,1,0]],//0 [[0,0,0],[1,0,0],[2,0,0],[0,0,1],[-1,0,1]],//1 [[0,0,0],[1,0,0],[1,-1,0],[2,-1,0],[3,-1,0]],//2 [[0,0,0],[1,0,0],[1,0,1],[2,0,1],[3,0,1]],//3 [[0,0,0],[1,0,0],[2,0,0],[2,-1,0],[3,-1,0]],//4 [[0,0,0],[1,0,0],[2,0,0],[2,0,1],[3,0,1]],//5 [[0,0,0],[1,0,0],[2,0,0],[2,1,0],[3,1,0]],//6 [[0,0,0],[1,0,0],[0,0,1],[-1,0,1],[-2,0,1]],//7 [[0,0,0],[0,1,0],[1,1,0],[1,2,0],[1,3,0]],//8 [[0,0,0],[0,1,0],[0,1,1],[0,2,1],[0,3,1]],//9 [[0,0,0],[0,1,0],[-1,1,0],[-1,2,0],[-1,3,0]],//10 [[0,0,0],[0,1,0],[0,2,0],[0,0,1],[0,-1,1]],//11 [[0,0,0],[0,1,0],[0,2,0],[-1,2,0],[-1,3,0]],//12 [[0,0,0],[0,1,0],[0,0,1],[0,-1,1],[0,-2,1]],//13 [[0,0,0],[0,1,0],[0,2,0],[1,2,0],[1,3,0]],//14 [[0,0,0],[0,1,0],[0,2,0],[0,2,1],[0,3,1]],//15 [[0,0,0],[0,0,1],[0,0,2],[0,1,2],[0,1,3]],//16 [[0,0,0],[0,0,1],[0,0,2],[-1,0,2],[-1,0,3]],//17 [[0,0,0],[0,0,1],[0,0,2],[0,-1,2],[0,-1,3]],//18 [[0,0,0],[0,0,1],[0,0,2],[1,0,2],[1,0,3]],//19 [[0,0,0],[0,0,1],[0,1,1],[0,1,2],[0,1,3]],//20 [[0,0,0],[0,0,1],[-1,0,1],[-1,0,2],[-1,0,3]],//21 [[0,0,0],[0,0,1],[0,-1,1],[0,-1,2],[0,-1,3]],//22 [[0,0,0],[0,0,1],[1,0,1],[1,0,2],[1,0,3]]//23 ]; The order of assembly is determined by the puzzle itself: we collect from the bottom up, as soon as the level is filled completely, we proceed to the next. The order of the brute force is determined by the array of the positions of the elements in space. If, after partially filling the level for some free point, it is impossible to find a position, the previous element found is considered incorrect, the box is removed from the current state array, and the search continues.
As for visualization, we will execute the three-dimensional representation of the cube in the form of five sections along the Z axis, along the slice for each level.
The sections are 5x5 tables, filled with cells with non-negative numbers from the “box”. The cells are additionally painted with different colors to separate the puzzle elements from each other. To reduce the load, the state of the array will be displayed once per second or at critical moments: start, pause, stop while finding the answer. In addition, we’ll use a “save string” to work with which you can pause, make changes to the code and continue the search from the pause rather than from the beginning. Also, we will display the number of cycles (for the moment of the end of the cycle we will take the moment of displaying the current state of the array), the number of “iterations” for the last cycle and the total number of “iterations”.
Of the features it is worth noting that in the prelaunch, at the beginning, an array of possible positions is created for each coordinate box, in order to cut off the positions that cannot be located at this point in advance. Also for versatility added the ability to change the size of the "box" in all three coordinates. To increase the rendering speed, added an array of cells in the slicing tables.
Full code with comments:
- github
- JSFiddle
We start, we wait (it took me 114 cycles on Google Chrome, going through 96969659 options), we look at the answer and collect it in real life.
Answer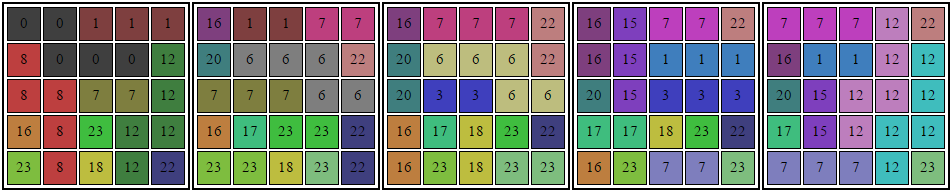

Save string for those who want to make a reflection check
[[5,0,0,0], [5,0,4,0], [12,3,0,0], [12,4,1,0]]
UPD According to Serator's advice , added the possibility of using web workers, however, it is not possible to parallelize the calculations, since the following calculation depends on the results of the previous one, so the calculations themselves were made separately for the web worker, and the visualization was left in the main thread.
The results of the work are shown below in the tables *. The fraction indicates the calculation time with the calculation tab active / with the calculation tab inactive. All additions and extensions at the time of calculation were disabled.
Using web worker **:
| Google Chrome 40.0.2214.115 (without hardware acceleration) | 168.08 seconds / 160.932 seconds |
|---|---|
| Google Chrome 40.0.2214.115 (with hardware acceleration) | 175.644 sec. / 168.802 sec. |
| Yandex Browser 12/14/2125.10034 | 163.975 sec. / 202.875 sec. |
| Internet Explorer 11 | 243.778 sec. / 246.766 sec. |
| Mozilla Firefox 35.0.1 | 731.949 sec. / 707.266 sec. |
| Opera 27.0.1689.69 | 213.088 seconds / 189.991 seconds |
Without a web worker:
| Google Chrome 40.0.2214.115 (without hardware acceleration) | 139.894 sec. / 1769.311 sec. |
|---|---|
| Google Chrome 40.0.2214.115 (with hardware acceleration) | 112.115 sec. / 1738.033 sec. |
| Yandex Browser 12/14/2125.10034 | 137.854 seconds / 1901.142 seconds |
| Internet Explorer 11 | 240.888 sec. / 227.489 sec. |
| Mozilla Firefox 35.0.1 | 173.205 sec / 2056.301 sec. |
| Opera 27.0.1689.69 | 130.07 seconds / 1904.973 seconds |
* - The results of the work depend on the total load of the machine, so the tables show the averaged values. The measurement error was about 5%.
** - The result of the work is presented when sending values to the visualization every 50 thousand searches, for the remaining values the result fit into the error.
You can check it yourself by running the script on the local web server.
In fact, the process of the calculation itself did not parallelize, so the time spent on the calculation with the web worker took more than without it, however, its use may be useful for carrying out the calculation in the background (when the calculation tab is inactive). In addition, Firefox turned out to be the slowest for settling with a web worker, and is comparable in time when performing calculations without it. Separately, it is worth noting that thanks to the web worker, visualization can be redrawn more often, which looks much more beautiful than without it.
Source: https://habr.com/ru/post/250807/
All Articles