Analysis of the problem “Mirror in the corridor” and outrage
I want to analyze in more detail the problem from the publication of the Olympiad on Programming among Schoolchildren , and also to show that it is really nontrivial. Although, as a result, the program consists of three assignments and two comparisons, it is not so easy to arrive at this result, especially if there is no reference book on analytical geometry at hand.
So, immediately agree that all rounding and errors associated with the representation of numbers with a floating point, we will not. We will work exclusively with integer variables, for this we will resort to obvious tricks. Although, in fact, there will be little programming and a lot of math. In this work, reference materials on university mathematics, or rather one paragraph from the chapter "Fundamentals of linear algebra and analytical geometry" [1], are used.
To begin, let me remind the text of the problem:
Well, "in the forehead" to this task does not approach, analysis in this topic is also not really something "chew". Therefore, I propose to simplify the problem and solve it for two-dimensional space, and then, by analogy, go to three-dimensional.
')
You can, of course, consider even a one-dimensional version, but there is little point in it, because the mirror turns into a point and Peter will see the person only when they are on one side of the mirror, i.e. if their coordinate has the same sign.
Draw an illustration to the task:
Let Petya be the point S , the stranger is the point T , the mirror is a straight line segment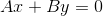
Baseline: R is the radius of the mirror, the coefficients A and B ;
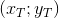- Coordinates entered;
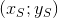- coordinates of Peter.
The solution algorithm is as follows:
- Through point T we draw a straight line, perpendicular to PQ ;
- On this straight line we mark the point T` symmetric to the point T relative to PQ - this will be the image of the person who entered (see or not see) Peter;
- We will make a direct ST` ;
- Find the intersection point of PQ and ST ` ;
- Check whether this point belongs to the segment PQ
So, the equation of a line passing through the point T is perpendicular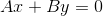 as follows:
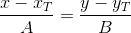or 
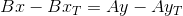
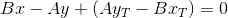
The point of intersection of TT` and PQ is the solution of the system of equations:
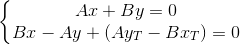
Multiply the equations by A and B, respectively, and add together:
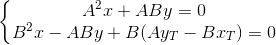
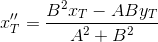
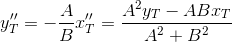
Found point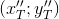
- projection of point T on the straight line PQ
Determine the coordinates of the point T` :
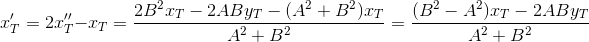
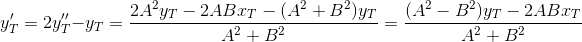
Two steps behind. Find the equation of the straight line ST` :
or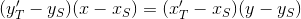 
Substitute the expression for the coordinates T` :
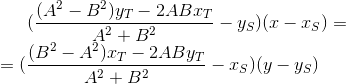
Going to integer calculus - multiply the equation by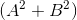
:
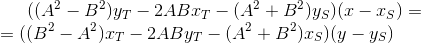
It's time to introduce a replacement:
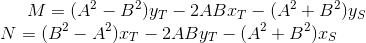
then the ST` equation takes the form: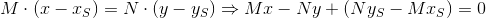
The point of intersection of PQ and ST ` is the solution of the system:
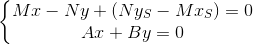
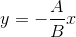
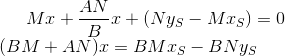
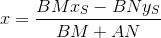
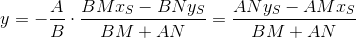
And finally, the distance from the center of coordinates to the found point: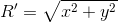
Leaving the radicals: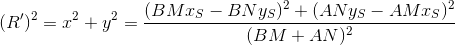
Now, if the found R ' is no more than the specified R , then our unfortunate Peter will still see the stranger who has entered.
Compared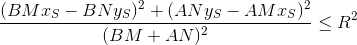
we multiply both sides of the inequality by a deliberately positive one (since even degree)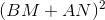 
those. we are interested in the truth of the expression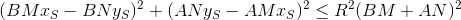
Why am I writing all this in detail? Just in order to show how much work the Olympiad participant must do to solve this problem, and after all all these formulas of perpendicular lines are not included in the school course of mathematics, the participant must himself reach them in a logical way? At the same time, he was assigned an average of 30 minutes to this task. So, the problem is still not solved in actual fact. First of all, we must do the same for the three-dimensional space, which is even more laborious, and secondly, it is not considered here whether the boy and his guest are on one side of the mirror ...
Well, we are not threatened with time trouble, so we will continue.
We will deal with the "mirror".
I have such a solution (although it also didn’t immediately occur to me, at first I was thinking about moving to the coordinate system associated with a direct mirror, but there are “ugly” trigonometric functions) - through the points S and T we will draw straight lines parallel to the given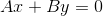 . Parallel lines have multiple coefficients for x and y , i.e. 
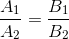, the difference is only in the free term. We will not invent anything and take these coefficients equal to the given A and B.
Then the equation of a line passing through the point S parallel to PQ has the form: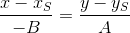
or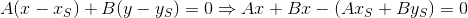 
Here, depending on the sign of a free member.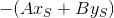
the straight line will be on one or the other side of the given one.
Similarly, for a line through T :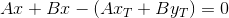
Do the following: find the value of the work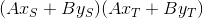
and compare it with zero: if it is greater than zero, the points are located on one side of the line, if it is less, they are different and Peter will not see his guest exactly, and the intermediate zero also satisfies, because in this case at least one of the points lies on the given line.
And finally, I will give the text of the program for the three-dimensional world, i.e. for the initial condition of the problem:
Sorry for the curvature of the code, I'm far from a programmer.
If you wish - I can attach and mathematical calculations for the three-dimensional world.
The moral of this publication is that the authors of tasks for olympiads should nevertheless check more carefully how difficult the task is and how much knowledge it requires for successful implementation in the allotted time.
1. Kornienko, V.S. Reference material in mathematics: A manual for self-education [Electronic resource] / V.S. Kornienko; Volgogr. state S.-H. Acad. Volgograd, 2010. 284 p.
So, immediately agree that all rounding and errors associated with the representation of numbers with a floating point, we will not. We will work exclusively with integer variables, for this we will resort to obvious tricks. Although, in fact, there will be little programming and a lot of math. In this work, reference materials on university mathematics, or rather one paragraph from the chapter "Fundamentals of linear algebra and analytical geometry" [1], are used.
To begin, let me remind the text of the problem:
Petya caught a cold in bed, when suddenly someone opened the door. Petya was too lazy to get up and he looked in the mirror to see who came. The coordinates of the person entered are known (it can be considered a material point), it is necessary to find out whether Petya will be able to see the reflection of the person who entered in the mirror. The mirror has the shape of a circle with a center at the origin of coordinates and is located in the plane ax + by + cz = 0. Petya can also be considered a material point. It is guaranteed that Peter and the stranger do not lie in the plane of the mirror and that Peter always sees the reflecting side of the mirror. If the image falls on the border of the mirror, then Petya sees the person who has entered. Since both Petya and the one who has entered can be considered material points, Petya can see the reflection of the one who has entered, both through the one who has entered and through his own reflection.
Well, "in the forehead" to this task does not approach, analysis in this topic is also not really something "chew". Therefore, I propose to simplify the problem and solve it for two-dimensional space, and then, by analogy, go to three-dimensional.
')
You can, of course, consider even a one-dimensional version, but there is little point in it, because the mirror turns into a point and Peter will see the person only when they are on one side of the mirror, i.e. if their coordinate has the same sign.
Draw an illustration to the task:
Let Petya be the point S , the stranger is the point T , the mirror is a straight line segment
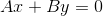
Baseline: R is the radius of the mirror, the coefficients A and B ;
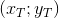- Coordinates entered; 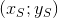- coordinates of Peter.The solution algorithm is as follows:
- Through point T we draw a straight line, perpendicular to PQ ;
- On this straight line we mark the point T` symmetric to the point T relative to PQ - this will be the image of the person who entered (see or not see) Peter;
- We will make a direct ST` ;
- Find the intersection point of PQ and ST ` ;
- Check whether this point belongs to the segment PQ
So, the equation of a line passing through the point T is perpendicular
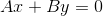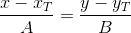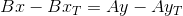
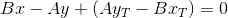
as follows: or The point of intersection of TT` and PQ is the solution of the system of equations:
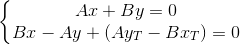
Multiply the equations by A and B, respectively, and add together:
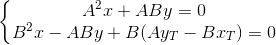
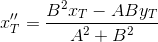
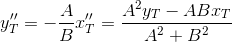
Found point
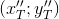- projection of point T on the straight line PQDetermine the coordinates of the point T` :
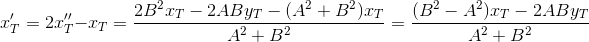
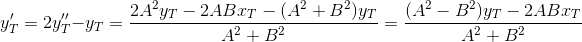
Two steps behind. Find the equation of the straight line ST` :
or 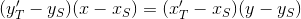Substitute the expression for the coordinates T` :
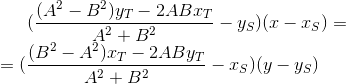
Going to integer calculus - multiply the equation by
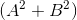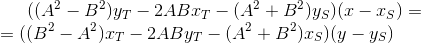
:It's time to introduce a replacement:
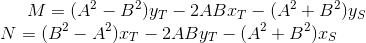
then the ST` equation takes the form:
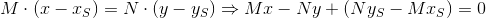
The point of intersection of PQ and ST ` is the solution of the system:
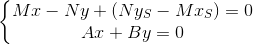
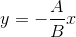
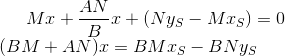
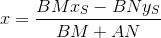
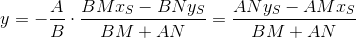
And finally, the distance from the center of coordinates to the found point:
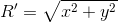
Leaving the radicals:
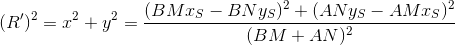
Now, if the found R ' is no more than the specified R , then our unfortunate Peter will still see the stranger who has entered.
Compared
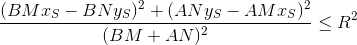we multiply both sides of the inequality by a deliberately positive one (since even degree)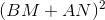 those. we are interested in the truth of the expression
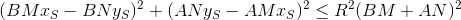
Why am I writing all this in detail? Just in order to show how much work the Olympiad participant must do to solve this problem, and after all all these formulas of perpendicular lines are not included in the school course of mathematics, the participant must himself reach them in a logical way? At the same time, he was assigned an average of 30 minutes to this task. So, the problem is still not solved in actual fact. First of all, we must do the same for the three-dimensional space, which is even more laborious, and secondly, it is not considered here whether the boy and his guest are on one side of the mirror ...
Well, we are not threatened with time trouble, so we will continue.
We will deal with the "mirror".
I have such a solution (although it also didn’t immediately occur to me, at first I was thinking about moving to the coordinate system associated with a direct mirror, but there are “ugly” trigonometric functions) - through the points S and T we will draw straight lines parallel to the given
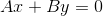. Parallel lines have multiple coefficients for x and y , i.e. 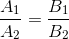, the difference is only in the free term. We will not invent anything and take these coefficients equal to the given A and B.Then the equation of a line passing through the point S parallel to PQ has the form:
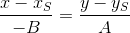or 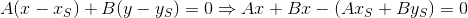Here, depending on the sign of a free member.
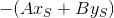the straight line will be on one or the other side of the given one.Similarly, for a line through T :
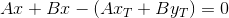
Do the following: find the value of the work
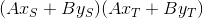and compare it with zero: if it is greater than zero, the points are located on one side of the line, if it is less, they are different and Peter will not see his guest exactly, and the intermediate zero also satisfies, because in this case at least one of the points lies on the given line.And finally, I will give the text of the program for the three-dimensional world, i.e. for the initial condition of the problem:
src
package ru.andrewn; import static java.lang.System.out; public class Program { public static void main(String[] args) { java.util.Scanner sc = new java.util.Scanner(System.in); out.println(" r:"); int R = sc.nextInt(); out.println(" a, b c:"); int A = sc.nextInt(); int B = sc.nextInt(); int C = sc.nextInt(); out.println(" (x, y z):"); int xx = sc.nextInt(); int yy = sc.nextInt(); int zz = sc.nextInt(); out.println(" (x0, y0 z0):"); int x0 = sc.nextInt(); int y0 = sc.nextInt(); int z0 = sc.nextInt(); if ( (A*x0+B*y0+C*z0)*(A*xx+B*yy+C*zz) >= 0 ) { int M = (B*B+C*CA*A)*x0-2*A*B*y0-2*A*C*z0-(A*A+B*B+C*C)*xx; int N = (A*A+C*CB*B)*y0-2*A*B*x0-2*B*C*z0-(A*A+B*B+C*C)*yy; int K = (A*A+B*BC*C)*z0-2*A*C*x0-2*B*C*y0-(A*A+B*B+C*C)*zz; if ( (A*M+B*N+C*K)*(A*M+B*N+C*K)*R*R >= ((B*N+C*K)*xx-B*M*yy-C*M*zz)*((B*N+C*K)*xx-B*M*yy-C*M*zz) + ((A*M+C*K)*yy-A*N*xx-C*N*zz)*((A*M+C*K)*yy-A*N*xx-C*N*zz) + ((A*M+B*N)*zz-A*K*xx-B*K*yy)*((A*M+B*N)*zz-A*K*xx-B*K*yy)) out.println(" "); else out.println(" "); } else out.println(" "); sc.close(); } } Sorry for the curvature of the code, I'm far from a programmer.
If you wish - I can attach and mathematical calculations for the three-dimensional world.
Summary
The moral of this publication is that the authors of tasks for olympiads should nevertheless check more carefully how difficult the task is and how much knowledge it requires for successful implementation in the allotted time.
Literature
1. Kornienko, V.S. Reference material in mathematics: A manual for self-education [Electronic resource] / V.S. Kornienko; Volgogr. state S.-H. Acad. Volgograd, 2010. 284 p.
Source: https://habr.com/ru/post/250763/
All Articles