The challenge of 64 coins, two prisoners and one chessboard

Translator's note : I replaced the original designations of the sides of the head / tail coin with obverse / reverse, so as not to confuse the Russian-speaking eagle / tails. In the illustration above on the left, the obverse (head), on the right, the reverse (tail).

Is salvation impossible?

This is one of those typical mysteries about prisoners in which you are sentenced to death and can be saved only if you prove your mental abilities to the jailer. You and your friend were imprisoned. Your jailer offers you a trial. If you follow it, both of you will be released.

Rules:

• The jailer takes you to a separate cell. The chamber contains a chessboard and a bank with 64 coins.
• The jailer takes the coins one by one and puts them on each cell of the board. He places the coins arbitrarily - some will be turned upside down, some - reverse (or all will be obverse, or reverse, you have no idea, everything is at the discretion of the jailer). If you try to intervene in the process of the layout of coins, it will result in immediate death. If you try to force, advise or convince the jailer in any way - immediate death. You can only watch.
• When all the coins are laid out, the jailer points to one of the cells and says: “This!” The indicated cell, “magic,” is your key to freedom.
• The jailer will allow you to flip one coin on the board. Only one, but it can be any coin of your choice. This is the only change you are allowed to make in the jailer's layout.
• Then you will be taken out of the room. If you try to leave any messages or tips for your friend ... yes, you guessed it, an immediate death!
• The jailer will take your friend to the room.
• Your friend will have to inspect the board (it is forbidden to touch) and decide where, in his opinion, the “magic” cell is located.
• He has only one try. Based on the location of the coins, he must point to the cell and say: “This!”
• If he indicates correctly, both of you will be pardoned and immediately released. If not, then both of you are executed.
• The jailer explains these rules to both of you in advance and gives time to confer to develop a strategy.

Is it possible to develop a strategy?

At first glance, this problem can not be solved. We can not influence the jailer, the layout of the coins can be any, and we have no idea which jail cell will indicate (in fact, he himself may not know which cell he will choose).
')
64 cells he can point to. 2 ⁶ possible answers. We need 6 bits of information to accurately identify the cell. If you flip a coin, this is one bit of information. Since we cannot convey the status of the “before” board, our friend does not have the opportunity to indicate which coin was turned upside down. Think, if a friend enters the room and sees 63 obverse and 1 reverse, he cannot know that the only reverse is the coin that you turned over, or there was a board with 62 obverse and 2 reverse, and you turned one reverse!

Is it possible to transfer 6 bits of information by inverting a single coin?

There is a strategy that allows you to escape with 100% probability regardless of the layout of the coins and the position of the "magic" cell. The decision does not imply any fraud or tricks, it is purely mathematical.

Start

The problem can be solved, because in fact we have more information than one bit transmitted between you and your friend. The location of the remaining coins stores information, and we can use it. In fact, we have a sufficient number of (six) controlled bits in the layout of the coins, with which we can identify any cell on the board.

Two cells

Imagine that we have a board with only two cells. There are 4 possible options for the location of the coins (A - obverse, P - reverse): PP, AA, RA, AP.



The jailer can choose as the "magic" as the first cell, and the second.
In advance, we agree on one rule - if the jailer points to the first cell (white), then it is necessary to make sure that the first cell has an obverse. Possible options:



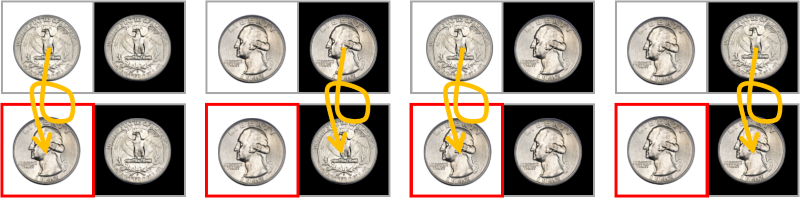
If the layout was PP, I can flip the first coin obverse, if AA - I will flip the second coin, since the first one is already turned obverse (according to our rule this will not change anything, but I have to flip the coin).
In all variants above, the obverse turned out to be on the first cell. According to our rule, this means that the jailer chose the first cell.

Similarly, if the jailer points to the second cell, I will make sure that the first cell does not have an obverse. This is a clue to my friend that the "magic" cell is not the first.



In all cases, the first cell is not obverse. By our rule, this means that the jailer chose the second cell.

Problem solved!

Induction

Mathematicians (and some programmers) will tell you that this is all we need to prove that solving a problem is possible. If we can encode one bit of information using two cells, then with the help of mathematical induction we can confirm that it is possible to encode 2 bits in 4 cells, 3 - in 8 ... 6 bits - in 64 cells.

Binary representation

If we mark cells from 0 (top left) to 63 (bottom right) in binary representation, we can display which part of the nested set each cell is.

The original article posted an interactive image of the board. The number in the lower left corner displays the cell number in binary notation. Each digit represents the set to which the cell belongs. A unit in any position indicates that the cell is in one half of the set, zero - in the other. By definition, each cell is unique and has an individual set of bits.

Parity

Instead of using two cells as in the simple example above, we divide the board into different combinations of two sets. Applying the same labeling rule to these two regions / sets as with single cells - we will designate if there is a “magic” cell in the first or second region.

Since the regions are collections of cells, we cannot simply rotate all the coins in the region obverse. Instead, we will flip one coin. We can count the number of obverse in the region - if their number is odd, we take it as a unit, if even - zero. Turning one coin in a region will change the number of obverse from odd to even, and vice versa (adding / subtracting one to any number inverts its parity / oddness).

This is the concept of parity. Switching from one state to another by adding or subtracting one bit is widely used in computers.

To change the parity of the region, we just need to turn one coin in it.

Using masks of powers of two, we can divide the board into regions in several ways. Below are shown various ways of dividing a board based on the state of bits (power of two) in a cell number. Combining these filters allows you to define a single cell that can be flipped to change the parity of any / all bits.



2 ^{0 is} equivalent to the logical “AND” (AND) from 000001, 2 ¹ - 000010 ... 2 ⁵ - 100000.

By definition, each cell has a unique set of bits. We can flip a single coin to change the parity of any combination of these filters.

The layout created by the jailer has its own (natural) parity. Coins are arranged arbitrarily, and we can calculate parity (the number of obverse) in each region. The combination of these parity bits will give us a random six-bit number.

To identify the "magic" cell, we need just six bits, and we can encode them using parity. We know that we can turn over any one coin, and this will lead to a change in one / several bits of a number. All we need is to find the necessary coin, the inversion of which will change the combination of the parity bits in such a way that the necessary number is obtained (a binary record of the number of the “magic” cell).

Together

Here I again send readers to an interactive model in the original article .


On the left board you can choose the location of the "magic" cells. The number on the right is the number of the selected cell (Target = ...), on the left is its binary representation.

The board on the right shows the layout of the coins. Only the obverse is depicted (for reasons of clarity), the reverse is indicated by empty cells. The "Random" button fills the board with a new random set of coins. The Clear button reverses all coins.

Under the right board, the board’s own parity is shown in gray on the left; the number of the coin to be turned is green on the right. On the left, under its own parity, the same number is written in binary form.

Where do these values ​​come from?

We already know where the number under the left board came from. This is just a binary description of the cell, each bit of the number indicates whether or not this coin is present in the filter-powers of the two shown above.

The gray number under the right board shows the parity of the board. For each filter, we find whether an even or an odd number of obverse is located in this region. A unit in any digit of the number indicates that there is an odd number of obverse in this region.

The green number indicates the number of the cell whose state you want to change (turn the coin) so that the parity of the board corresponds to the desired number of the “magic” cell. It is calculated by executing a bit operation exclusive “OR” (XOR) on the board's own parity and the desired value.

Exclusive "OR"

The XOR operator is widely used in programming. He has some interesting properties. If the exclusive "OR" is applied twice with the same value, it will return the initial state:

(A XOR B) XOR B = A

Also, if we apply XOR to any number and complete set of bits (a number consisting of one units), all the bits of the original number will be inverted. Applying XOR to a number and some set of (set) bits inverts these bits in the original number and preserves the state of the others.

That is why we used the XOR operator to calculate the position of the coin. For each bit of parity, regardless of whether it already contains the correct value, and we want to save it (XOR c 0), or we want to switch it (XOR c 1).

Example:
If the number of the "magic" cell is 101001 (41) and the parity of the board is 010101, then we need to turn the coin in the cell 111100 (60):

You can also use XOR to quickly calculate the board's own parity. To do this, you need to go around the entire board once and perform this operation on each value (sequence number) of the cell with the obverse.

Math can save your life!