Lock-free data structures. Concurrent maps: rehash, no rebuild

Let's follow in the footsteps of C ++ 2015 Russia further.
In the previous article, we reviewed the algorithm for the lock-free ordered list and, based on it, made the simplest lock-free hash map. This hash map has a flaw: the size of the hash table is constant and cannot be changed as the number of elements in the container grows. This is not a problem if we roughly represent the required container volume in advance. And if not?

The procedure for increasing, as well as reducing, the size of the hash table (rehashing) is quite heavy

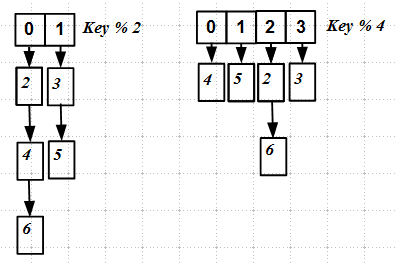
As can be seen even from this simple picture, when rehasing, the keys are redistributed to other slots of the new hash table, there is a complete restructuring of the hash map. It is quite difficult to implement atomic or at least without locks.
Many times I mentioned Nir Shavit together with Ori Shalev looked at the problem from the other side: well, we can not atomically redistribute the keys to new slots (buckets), but maybe we can just insert a new bucket into an existing one, thus breaking (splitting) it into two parts? This idea formed the basis of the split-ordered list algorithm developed by them in 2003.

Split-ordered list

You cannot just take and insert a new bucket, - see the picture above: the keys are re-distributed between the buckets when rehashing, and we need their positions not to change. We want something strange like this:

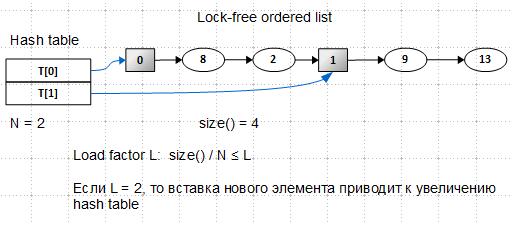
It is based on the lock-free ordered list already reviewed by us. Two types of nodes appeared in it: regular nodes (oval) and auxiliary (sentinel) nodes (square). Auxiliary nodes play the role of starting marks for buckets and are never deleted; The hash table contains pointers to these auxiliary nodes.
Looking at this picture, you can ask: the list is ordered, but this is not visible - the keys are arranged chaotically, what's the matter? Answer: the list is ordered , but we will invent the order criterion a little later.
So, we have a hash table with two slots pointing to the auxiliary nodes. The size of the list is 4 (auxiliary nodes are not taken into account when counting the number of elements), load factor is 2 (this is my voluntarist solution). We want to insert a new item with key 10:

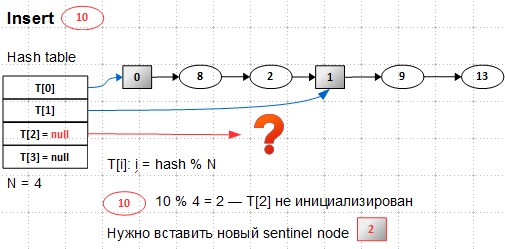
When we try to insert new elements, we find out that our list is full - the number of elements becomes 5, the number of buckets is 2, 5/2 > load factor , - we need to extend the table T[] . Suppose we have somehow expanded it - it has 4 buckets, the first two are initialized, the last two are not. The new element 10 should get into the bucket 2 ( 10 mod 4 = 2 , hereinafter I consider for clarity that hash(key) == key ), which is not yet initialized. So, you first need to insert auxiliary element 2, that is, to make the splitting of some existing bucket. First you need to find this existing bucket, called the parent :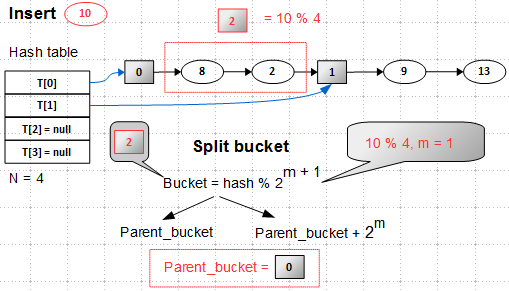

The splitting bucket is perhaps the most subtle point in the algorithm. The parent bucket, which is not yet known to us, must be in the first half of the hash table, that is, in our case, this is bucket 0 or 1.
Bucket is hash(key) mod 2**(m+1) , where 2**(m+1) is the size of the hash table. The new bucket splits the parent, that is, it divides the elements of the parent bucket into two camps: some are in the parent bucket, and the second are in the parent_bucket + 2**m . It follows that for the new bucket 2 the parent is bucket 0.
In C ++, the procedure for calculating the parent bucket looks very simple:

  size_t parent_bucket( size_t nBucket ) { assert( nBucket > 0 ); return nBucket & ~( 1 << MSB( nBucket ) ); } 

where MSB is the most significant bit - the number of the most significant single bit.

So, to insert element 10, first of all you should create a new bucket 2 and insert it into bucket 0. We have a ready- ordered list algorithm, so it's time to decide how our split-ordered list should be ordered.
Note that all the operations that we have done so far have been based on arithmetic modulo two. Let's look at the binary representation of the keys:

And now - attention: if you read the binary key values from right to left , we get a sorted list:

I call such reversed hash values ​​shah.
So, the list sorting criterion is based on reversed (read from right to left) key hash values.

It turns out interesting: bucket'y calculated by the hash values ​​of the keys, and sorting by reversed hash values. The main thing - do not get confused.
But that's not all. Looking at the picture again, we will see that the node with key 2 is already in the list — this is a regular node, and we need to insert an auxiliary with the same key. Auxiliary and regular nodes are completely different objects, even in their internal structure: regular nodes contain a key and a value (value), and auxiliary ones that serve as marks of the beginning of buckets, only hash values. A regular node can be removed from the list, but never a secondary node. Therefore, we need to somehow distinguish these two types of nodes. The authors propose to use for this the most significant bit of the hash value (in the converted hash value it will be the least significant bit): in the hash values ​​of the regular nodes, the most significant bit is set to 1, and in the auxiliary bits it is set to 0:

This bit also plays the role of a limiter when searching for a key in a bucket, - we never get out of the bucket’s boundaries.
')
To summarize all of the above. Key 10 is inserted in two stages: first, a new auxiliary node 2 is added to the parent bucket 0:

Then an element with the key 10 is inserted into the bucket 2:

The split-ordered list is based on the lock-free ordered list, which we discussed in the previous article , so there should be no difficulty inserting / deleting. By the way, about deleting, - the algorithm does not have any special features for deleting from the split-ordered list, we simply calculate the bucket using the key and call the delete function from the lock-free list with the start in the auxiliary node of this bucket. Auxiliary nodes are never deleted, that is, a hash table in a split-ordered list can only grow dynamically, but not shrink.

The split-ordered list algorithm is interesting in that it contradicts all canonical ideas about hash tables. Recall that Knut, in his monograph, proves that in order to build a good hash table, its size must be a prime number, therefore, all arithmetic must be modulo prime numbers. For a split-ordered list, the opposite is true: this algorithm relies heavily on a binary representation of hash values, all arithmetic is modulo-two. Such sharpening under 2**N fits very well on modern processors, which, despite significant progress, are still blunt on integer division, but they really like the replacement of division by shifts.

There remains one unexplained question - the dynamic extension of the hash table. The authors propose a segment organization of the hash table:

Instead of a single T[N] array, the Segment[M] segment array is used, which is created when the split-ordered list object is initialized. Here M is a power of two. The segment number is the most significant bits of the hash value. Each segment points to the T[N] table, these tables are created dynamically as needed, except for the Segment[0] table, which is initialized when the split-ordered list object is created (remember, I noted that bucket 0 should always be).
With such an organization, at the time of creating the list object, you still need to know the expected number of elements in order to calculate the size of the table of segments M (there is no special algorithm for this calculation — I have selected some boundaries empirically so that both Segment[] and each T[] are comparable in size). But still, the algorithm allows the growth of the hash table, albeit in such an unusual form.

Results

This article describes a very original lock-free split-ordered list algorithm that allows you to do rehash without rebuild, that is, without rebuilding the hash table. This algorithm is also interesting because it basically has a regular lock-free ordered list and can be used as a testing ground for debugging various implementations of ordered lists.
The implementation of this algorithm in libcds shows very good results in tests, but it is still slightly worse than the simplest hash map described in the previous article. There are two reasons for this:

• This is a fee for dynamically generated buckets.
• reversing the order of the hash value bits is still quite a hard operation if it is implemented programmatically. It would be interesting to have this operation in the gland

From an architectural point of view, it was very exciting to develop this algorithm in order to highlight the ordered list as a strategy for the split-ordered list.

In the next article I will talk about another reincarnation of the lock-free ordered list. This time we will not build a hash map, but an ordered map.