Binary operations on ordered sets
In the previous article I wrote about binary operations on disordered sets . In this article we will look at algorithms with less complexity of execution, for ordered sets.
Content
I. Intersection of ordered sets
Ii. Difference of ordered sets
Iii. Union of ordered sets
Iv. Symmetric difference of ordered sets
Conclusion
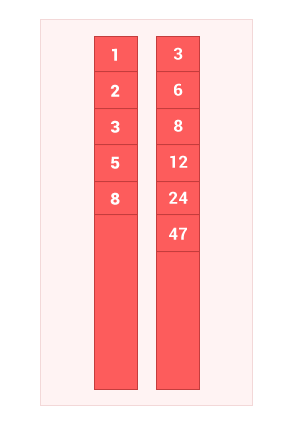
The intersection of two ordered sets A and B is a set with only those elements A and B that simultaneously belong to both sets, without duplicates. The complexity of the algorithm is O (m + n) , where m and n are the lengths of the input sets A and B, respectively.
')
Made a little animation to show how the algorithm works.
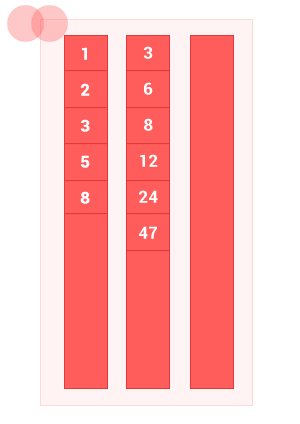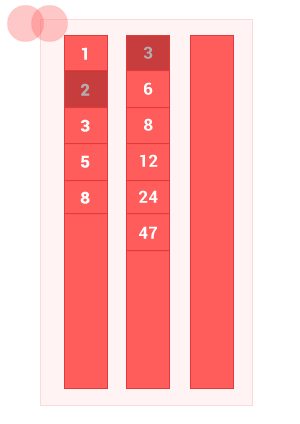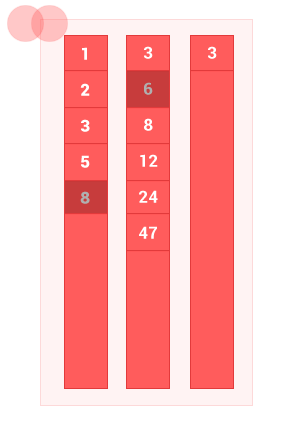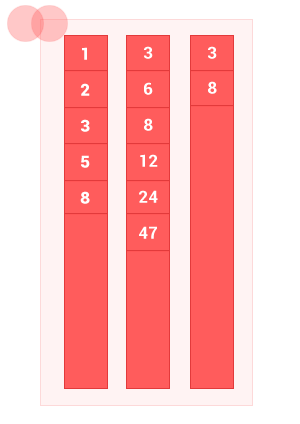
Javascript implementation example:
Function call:
The difference of two ordered sets A and B is a set with elements A that do not coincide with elements B , without duplicates. The complexity of the algorithm is O (m + n) , where m and n are the lengths of the input ordered sets A and B, respectively.
The union of two ordered sets A and B is a set with elements A and elements of set B , without duplicates. The complexity of the algorithm is O (m + n) , where m and n are the lengths of the input ordered sets A and B, respectively.
The symmetric difference of two ordered sets A and B is a set that includes all those elements of the first ordered set that are not in the second ordered set, as well as those elements of the second ordered set that are not included in the first ordered set. The complexity of the algorithm is O (2 (m + n)) , where m and n are the lengths of the input ordered sets A and B, respectively.
In essence, this is the subtraction of sets, first A from B , then B from A.
The method proposed by 0leGG .
I often have to work with sorted arrays, so these algorithms greatly accelerate the process. An example of the implementation of the intersec_sort_arr method, you can see in my application for vk.com. Using this method, I find common community members working with sorted arrays, in millions of elements, the method copes very quickly. Prior to that, I used the method described in my previous article , array processing was very slow.

Content
I. Intersection of ordered sets
Ii. Difference of ordered sets
Iii. Union of ordered sets
Iv. Symmetric difference of ordered sets
Conclusion
I. Intersection of ordered sets
The intersection of two ordered sets A and B is a set with only those elements A and B that simultaneously belong to both sets, without duplicates. The complexity of the algorithm is O (m + n) , where m and n are the lengths of the input sets A and B, respectively.
')
Made a little animation to show how the algorithm works.

Javascript implementation example:
function intersec_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) // { if (array_1[i] == array_2[j]) { array_3[k] = array_1[i]; // array_3 k++,i++,j++; // 3 } else { if (array_1[i] < array_2[j]) { i++; // } else { j++; // } } } return array_3; } Function call:
intersec_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // [3, 8] Ii. Difference of ordered sets
The difference of two ordered sets A and B is a set with elements A that do not coincide with elements B , without duplicates. The complexity of the algorithm is O (m + n) , where m and n are the lengths of the input ordered sets A and B, respectively.

function diff_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) // { if (array_1[i] == array_2[j]) { i++,j++; } else { if (array_1[i] < array_2[j]) { array_3[k] = array_1[i]; k++; i++; // } else { j++; // } } } while (i < n) { array_3[k] = array_1[i]; k++, i++; } return array_3; } diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // [1, 2, 5] Iii. Union of ordered sets
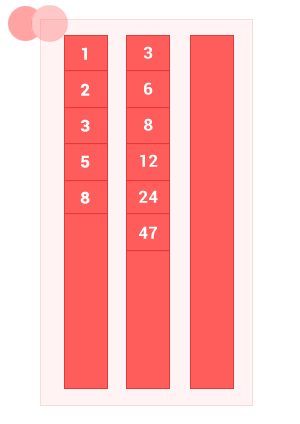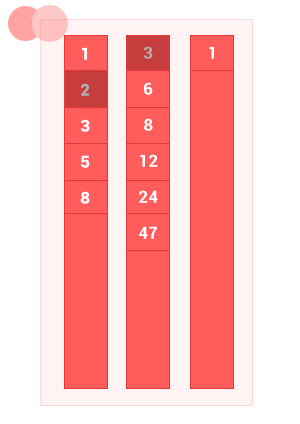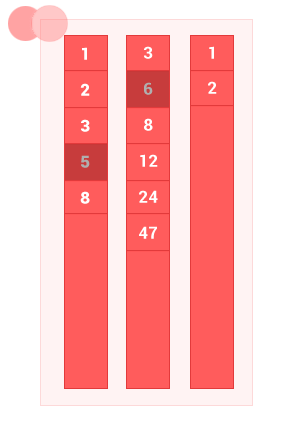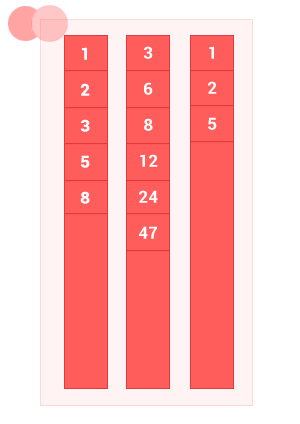
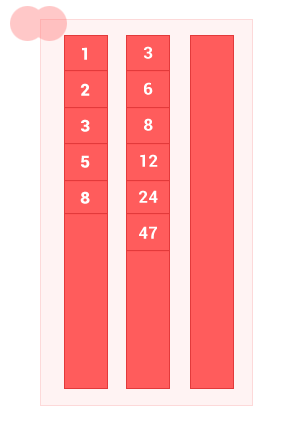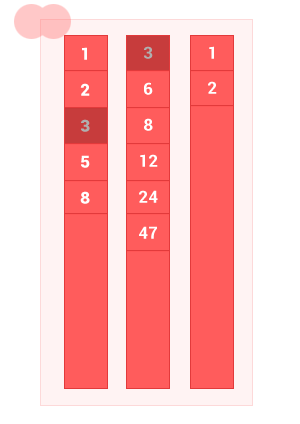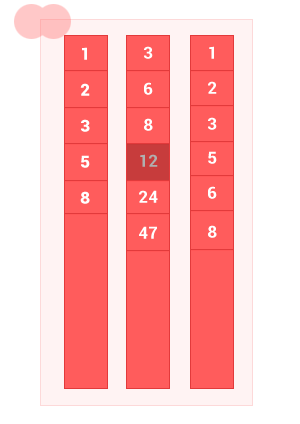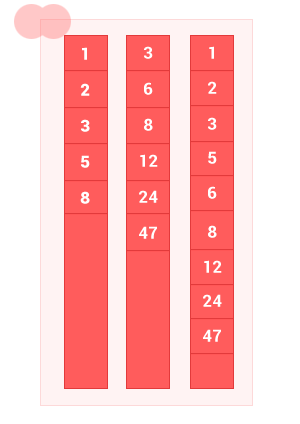
The union of two ordered sets A and B is a set with elements A and elements of set B , without duplicates. The complexity of the algorithm is O (m + n) , where m and n are the lengths of the input ordered sets A and B, respectively.

function sum_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) // { if (array_1[i] == array_2[j]) { array_3[k] = array_1[i]; k++,i++,j++; } else { if (array_1[i] < array_2[j]) { array_3[k] = array_1[i]; k++; i++; // } else { array_3[k] = array_2[j]; k++; j++; // } } } while (i < n) { array_3[k] = array_1[i]; k++, i++; } while (j < m) { array_3[k] = array_2[j]; k++, j++; } return array_3; } sum_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // [1, 2, 3, 5, 6, 8, 12, 24, 47] Iv. Symmetric difference of ordered sets
The symmetric difference of two ordered sets A and B is a set that includes all those elements of the first ordered set that are not in the second ordered set, as well as those elements of the second ordered set that are not included in the first ordered set. The complexity of the algorithm is O (2 (m + n)) , where m and n are the lengths of the input ordered sets A and B, respectively.
In essence, this is the subtraction of sets, first A from B , then B from A.
2 passes
function symmetric_diff_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) // { if (array_1[i] == array_2[j]) { i++,j++; } else { if (array_1[i] < array_2[j]) { array_3[k] = array_1[i]; k++; i++; // } else { j++; // } } } while (i < n) { array_3[k] = array_1[i]; k++, i++; } n = array_2.length, m = array_1.length, j = 0, i = 0; while ((i < n) && (j < m)) // { if (array_2[i] == array_1[j]) { i++,j++; } else { if (array_2[i] < array_1[j]) { array_3[k] = array_2[i]; k++; i++; // } else { j++; // } } } while (i < n) { array_3[k] = array_2[i]; k++, i++; } return array_3; } The method proposed by 0leGG .
1 pass
function symmetric_diff_sort_arr(array_1,array_2) { var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = []; while ((i < n) && (j < m)) // { if (array_1[i] < array_2[j]) { array_3[k] = array_1[i]; k++; i++; // } else if (array_1[i] > array_2[j]) { array_3[k] = array_2[j]; k++; j++; // } else { i++, j++; } } while (i < n) { array_3[k] = array_1[i]; k++, i++; } while (j < m) { array_3[k] = array_2[j]; k++, j++; } return array_3; } symmetric_diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // [1, 2, 5, 6, 12, 24, 47] Conclusion
I often have to work with sorted arrays, so these algorithms greatly accelerate the process. An example of the implementation of the intersec_sort_arr method, you can see in my application for vk.com. Using this method, I find common community members working with sorted arrays, in millions of elements, the method copes very quickly. Prior to that, I used the method described in my previous article , array processing was very slow.
Source: https://habr.com/ru/post/250191/
All Articles