Crossword Formation Algorithm
This story begins with the publication of "The most difficult crossword made by computer . " It contains one of the most difficult crossword puzzles compiled by the program (see below).

I was sure that all crosswords were generated programmatically long ago and was somewhat surprised that this could be a problem. I note that we are talking about “Canadian” crossword puzzles, in which each word intersects with another word on each letter or is very close to them in complexity. In my work as an analyst, there are not so many really difficult tasks, so it became interesting for me to try to develop an algorithm that could do this. The result of thinking, supported by the program for generating crossword puzzles, is given in this article.
Busting is always used to complete a crossword puzzle. We put the first word, then all of the following, checking that the letters at the intersections coincide with the letters in the words put earlier. And so, until all the words are put. It would seem - there is nothing easier. However, a simple count of the number of iterations of word selection for a crossword of medium length by 50 words can change this opinion. So, to install any word except the first one, if there are 1,000 words of the appropriate length in the database and there is only one previously filled word at the intersection, on average we need 1,000/33 = 30 iterations (we, on average, will need to look through 30 words before we come across a word that has the desired letter at the position of the previously filled intersection). If there is more than one intersection word filled earlier, this number will increase dramatically. A simple calculation shows that in order to fill 50 words, we need to perform 30 ^ (50-1) iterations. These are billions of billions of iterations. Even on modern computers, it will require days and months of work. And here in the first place is not the actual search, but the algorithm, which will allow to reduce the time for generating a crossword puzzle by many orders of magnitude.
')
Immediately, “ashore”, we must accept that the generation of the crossword puzzle will consist of two stages:
Based on this, I will mark the decisions below, which stage they apply to.
All experiments will be placed on the crossword, shown in the figure below.

This is not the most difficult crossword puzzle, but solutions that are relevant to it will be relevant for all other crossword puzzles. And a small number of words guarantees us a relatively quick result.
And the last. The article will omit all that relates to the generation of a database of words for the program. This part "cost" at least 50% of the total time spent. Now in the database of more than 158 thousand words, of which more than 125 thousand are unique. The base has been cleaned to the maximum extent in a software way, but still requires attention in the manual mode. I did not in any way close or encrypt the database - it lies open in text form and the simplest key-value format. You can delete or add words to it, correct the descriptions or completely replace it with your own (for example, in another language).
The first thing to determine - the sequence of filling words. For this there are very simple and obvious solutions.
Decision number 1: Words will be generated in a sequence that depends primarily on their length. The longer the word, the more it can have intersections and the harder it will be to find the word to install. On the contrary, the shortest words, 2 or 3 letters long, will have the minimum number of intersections and are most conveniently selected at the final stage of generation. This solution is used at the analysis stage.
Decision number 2: Of the words with the same length, the words with the greatest complexity of installation will be installed first. Installation complexity is a calculated parameter that shows “how difficult it will be to pick up a value in this word” and “how much the cost of an error will be if the word cannot be picked up”. It is clear that words of the same length, for example, 5 letters, can intersect both with one word and immediately with five, and the complexity of the installation will be completely different. This solution is used at the analysis stage.
Decision number 3: Taking into account the previous decisions, our words are arranged in a sequence that does not guarantee the intersection of two adjacent words with each other. This means that if we did not find the word to be installed, then it is not the previous word that needs to be changed, but one of the previously established words that intersect with this word and in essence set the selection conditions for it. It is logical of all the previously established intersection words to replace the last word set in order to roll back to the minimum number of generation words. This solution is used at the generation stage.
If you track the installation of words in the sequence that was determined on the basis of decisions No. 1 and No. 2, you will notice that the installation of some words forms locally independent fragments. Look at the picture below.
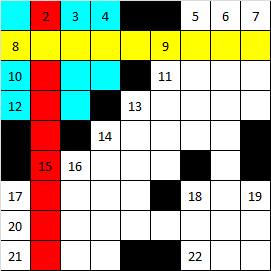
The picture shows the sequence of installation of the first words in the crossword grid in the order corresponding to the well-known "Every hunter wants to know where the pheasant sits." The first word to be marked is red. After it is a word marked yellow, etc. After installing only 2 words in a crossword puzzle a local fragment was formed, marked in blue.
Before continuing, we first define the terminology:
When a fragment appears, a dilemma arises - either continue generating a crossword puzzle in a previously defined sequence, or first generate all the words of the fragment to verify the correctness of the starting word. This is one of the places of the algorithm, which can critically affect its overall performance and which does not have a clear logical solution.
Solution # 4: A fragment search will be performed for each word to be installed. All words belonging to the same fragment will have a sequential installation sequence, starting from the start word, or from the first word of the fragment. This solution is used at the analysis stage.
At the moment, part of the algorithm for changing the sequence of generating words of fragments is as follows:
Actually, this is all - the algorithm for generating a crossword puzzle is done by brute force. With minimal detail, it looks like this:
Checked - it really works on the grids to the average level of complexity. However, as the crossword grid becomes more complex and the number of words increases, the number of successful attempts at generation tends to 0. Actually, from this moment the most interesting begins.
The first question that comes to mind is it possible to somehow reduce the number of kickbacks? After all, each rollback to a few words back can cost tens and hundreds of thousands of iterations. The logical step is to add rules that reduce the number of mistakes in the installation of words, like, do not put a soft or hard sign in the cell where the word begins, etc. If you don’t crawl deeply, it’s quite simple to describe most of these rules for the Russian language, but there is a problem - they will be absolutely useless, for example, for English. I also wanted to make a universal algorithm that does not depend on the language.
Reflections on this issue led to the following: “it would be good if for every unspecified word that crosses the currently installed word, the availability of options for the installation is guaranteed”.
So the idea was to use templates like the LIKE command in Transact-SQL. A pattern is a character string by which words will be compared. The template itself includes letters and template characters. During the comparison with the template, it is necessary that the letters exactly match the characters specified in the string. Template characters can match arbitrary elements of a character string.
Decision number 5: For each starting word, patterns of all words intersecting with it will be calculated. The starting word must have letters strictly from the list in the template corresponding to the position of the letter of the intersection. This solution is used at the generation stage.
Examples of patterns for words of three letters are given below:
On the example of the latter, the patterns should be read as follows: for a word of 3 letters, whose first two letters are equal to “BEFORE”, there are words in the database that have the last letter equal to one of “KMN”.
Let's go back to the fragments. Look at the picture below.
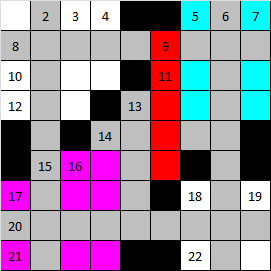
In it, the cells of the words set earlier are marked in gray. When you install the word marked in red, two fragments are formed at once, marked with blue and purple flowers.
If you look at the purple fragment, you will see that it is associated with the starting word with one single intersection. And it is beautiful! This gives us the opportunity to use another solution.
Some more terminology:
Solution # 6: If a fragment is unsuccessful, for which the starting word is an accelerator, the algorithm will store a list of letters that were set to the starting word at the intersection with one of the words of the fragment to block repeated settings of words that have these letters on the intersection. This solution is used at the generation stage.
The algorithm for using accelerators is given below.
First, how it works without an accelerator:
The fragment depth can be quite large, and the total number of iterations to fill a fragment can be in the millions. To iterate over all possible options, you need the number of iterations for a single filling of the fragment, multiplied by the number of words in the database with a length, like a starting word (of which there may be tens of thousands).
How it works with the accelerator:
The depth of the fragment is the same. However, to iterate over all possible options, you need to multiply the number of iterations to fill a fragment not by the number of options for the start word, but by only 33 (the number of letters in the alphabet).
The previous decisions have essentially exhausted the 20% of efforts that, according to the Pareto principle, give us 80% of the result. Further, it is necessary to use more and more complex approaches, with sometimes unclear prospects.
Once, when generating a crossword puzzle, the program gave the following message: “Bust time: 11,471 days ...”. This message appears only if all the variants were searched for the very first word and you need to find a new value for it. The program has already spent time simply multiplies by the remaining number of options. It amused me and made me wonder if this time could be converted into a result? The idea is to deliberately cut off some brute force options that have a minimal likelihood of success.
The main thesis of this decision is that even better the program will produce a negative result in the shortest possible time (i.e., among the most optimal options, selection failed) than it will be in selection so much time that all conceivable limits will be exceeded.
Decision number 7: When installing a word that intersects words with great complexity of installation, it is forbidden to put the letters in the position of the intersection, the frequency of which is used in words of intersections is minimal. This solution is used at the generation stage.
If simple, this solution discards a certain number of letters of the Russian alphabet (sometimes up to 20), increasing the chance to generate complex sections of words with the most frequently used letters (here in chocolate the Italian alphabet with its 21 letters). As a result, we will get more options for the selection of difficult to install words, when it comes to the turn, which means more chance for successful generation of the whole crossword puzzle.
There are also disadvantages - some of the brute force options will be irretrievably lost. Perhaps among them will be the one, the only possible option to fill the grid. Only you can get it in 30 years - you just need to wait a bit.
Another disadvantage is that long words with more than 10 intersections are blocked the most. This leads to the fact that the program can not start generation, blocking the first word, until the options for it end. This minus is only partially managed by reducing the degree of blocking, and hence the effectiveness of this solution.
To systematize grids by generation complexity, the attribute “Generation complexity” is introduced, which is calculated based on the number of words, their length, and the number of intersections. In fact - more or less stable result can be obtained with the complexity of up to 600 units. All that is higher - for good luck.
Below is shown the average generation time for 10 attempts for several grids arranged in order of increasing complexity of generation.

Simple test grid for experiences, with a small amount of words.
Subtotal: Grids of such complexity are generated quickly and stably.

This grid is more complicated. This is a small “Canadian” crossword puzzle, where all words have intersections on all letters.
Subtotal: Grids of such complexity in most cases are generated fairly quickly, however, sometimes the generation can take 10 minutes or more.

This rather complicated grid turned out to be quite “convenient” for generation.
Subtotal: Due to the fact that this grid is very well fragmented and intersections are not available on all letters of long words, the program generates it almost instantly.

But this grid already has a “target” complexity. This is a full-fledged "Canadian" crossword, though not the most difficult one.
Subtotal: The program handled! A successful generation result, at the very least, can be obtained in just 17 minutes. The average generation time is just over 4 minutes.

And finally - the most difficult crossword puzzle that started it all. It has 72 words, which is not so much. However, the complexity of the generation was very high. The main problem for generation are the four longest words with which almost all other words of the crossword cross. They are like bones of the skeleton, on which you need to strung all the other words. Kickbacks discard the generation process almost to the very beginning. Thus, the process of generating this grid can be compared with Sisyphus, pushing a stone up the hill. And every time there is very little to the goal, the stone rolls to the very beginning of the path.
Alas - this peak has remained unconquered! I ran several generations with different settings, with a limit of up to 10 hours in duration, but none of them was completed successfully. Time is clearly not enough. Who knows, maybe this unconquered peak will inspire someone for a new assault!
And yet yes! Generating a crossword puzzle, even for the most modern computers, is a difficult task. I am sure that the possibilities to improve this algorithm are far from exhausted, however, regardless of the capabilities of the algorithm and the power of the computer, you can always complicate the crossword grid a little more so that the program promises you a result in 20-30 years.
I hope you were interested, and you read to the end.

I was sure that all crosswords were generated programmatically long ago and was somewhat surprised that this could be a problem. I note that we are talking about “Canadian” crossword puzzles, in which each word intersects with another word on each letter or is very close to them in complexity. In my work as an analyst, there are not so many really difficult tasks, so it became interesting for me to try to develop an algorithm that could do this. The result of thinking, supported by the program for generating crossword puzzles, is given in this article.
Busting is always used to complete a crossword puzzle. We put the first word, then all of the following, checking that the letters at the intersections coincide with the letters in the words put earlier. And so, until all the words are put. It would seem - there is nothing easier. However, a simple count of the number of iterations of word selection for a crossword of medium length by 50 words can change this opinion. So, to install any word except the first one, if there are 1,000 words of the appropriate length in the database and there is only one previously filled word at the intersection, on average we need 1,000/33 = 30 iterations (we, on average, will need to look through 30 words before we come across a word that has the desired letter at the position of the previously filled intersection). If there is more than one intersection word filled earlier, this number will increase dramatically. A simple calculation shows that in order to fill 50 words, we need to perform 30 ^ (50-1) iterations. These are billions of billions of iterations. Even on modern computers, it will require days and months of work. And here in the first place is not the actual search, but the algorithm, which will allow to reduce the time for generating a crossword puzzle by many orders of magnitude.
')
On the track ...
Immediately, “ashore”, we must accept that the generation of the crossword puzzle will consist of two stages:
- Analysis - the creation of a generation plan, the main result of which is a certain sequence of word crossword generation and other data that will help in the generation phase.
- Generation - sequential filling of the crossword puzzle grid with words, using the method of complete enumeration of all possible options, taking into account the data obtained at the analysis stage.
Based on this, I will mark the decisions below, which stage they apply to.
All experiments will be placed on the crossword, shown in the figure below.

This is not the most difficult crossword puzzle, but solutions that are relevant to it will be relevant for all other crossword puzzles. And a small number of words guarantees us a relatively quick result.
And the last. The article will omit all that relates to the generation of a database of words for the program. This part "cost" at least 50% of the total time spent. Now in the database of more than 158 thousand words, of which more than 125 thousand are unique. The base has been cleaned to the maximum extent in a software way, but still requires attention in the manual mode. I did not in any way close or encrypt the database - it lies open in text form and the simplest key-value format. You can delete or add words to it, correct the descriptions or completely replace it with your own (for example, in another language).
The beginning of the way
The first thing to determine - the sequence of filling words. For this there are very simple and obvious solutions.
Decision number 1: Words will be generated in a sequence that depends primarily on their length. The longer the word, the more it can have intersections and the harder it will be to find the word to install. On the contrary, the shortest words, 2 or 3 letters long, will have the minimum number of intersections and are most conveniently selected at the final stage of generation. This solution is used at the analysis stage.
Decision number 2: Of the words with the same length, the words with the greatest complexity of installation will be installed first. Installation complexity is a calculated parameter that shows “how difficult it will be to pick up a value in this word” and “how much the cost of an error will be if the word cannot be picked up”. It is clear that words of the same length, for example, 5 letters, can intersect both with one word and immediately with five, and the complexity of the installation will be completely different. This solution is used at the analysis stage.
Decision number 3: Taking into account the previous decisions, our words are arranged in a sequence that does not guarantee the intersection of two adjacent words with each other. This means that if we did not find the word to be installed, then it is not the previous word that needs to be changed, but one of the previously established words that intersect with this word and in essence set the selection conditions for it. It is logical of all the previously established intersection words to replace the last word set in order to roll back to the minimum number of generation words. This solution is used at the generation stage.
Fragments
If you track the installation of words in the sequence that was determined on the basis of decisions No. 1 and No. 2, you will notice that the installation of some words forms locally independent fragments. Look at the picture below.

The picture shows the sequence of installation of the first words in the crossword grid in the order corresponding to the well-known "Every hunter wants to know where the pheasant sits." The first word to be marked is red. After it is a word marked yellow, etc. After installing only 2 words in a crossword puzzle a local fragment was formed, marked in blue.
Before continuing, we first define the terminology:
- Fragment - a group of words in the amount of from 1 word to 50% of the total number of words of a crossword, the generation of which does not depend on all other, not yet set words.
- The starting word is a word, after its installation a fragment was formed (in the figure above it is a word highlighted in yellow).
- The first word is the fragment word, which has the minimum order of installation from all the fragment words.
- The fragment depth is the number of words that make up the fragment.
When a fragment appears, a dilemma arises - either continue generating a crossword puzzle in a previously defined sequence, or first generate all the words of the fragment to verify the correctness of the starting word. This is one of the places of the algorithm, which can critically affect its overall performance and which does not have a clear logical solution.
Solution # 4: A fragment search will be performed for each word to be installed. All words belonging to the same fragment will have a sequential installation sequence, starting from the start word, or from the first word of the fragment. This solution is used at the analysis stage.
At the moment, part of the algorithm for changing the sequence of generating words of fragments is as follows:
- We find fragments.
- We determine the complexity of filling the fragment.
- We define the word, after which you need to place all the words of the fragment according to the following rules:
- Words that are members of the fragments, set one after another.
Actually, this is all - the algorithm for generating a crossword puzzle is done by brute force. With minimal detail, it looks like this:
- The sequence of word generation is determined.
- The selection and installation of the word with the previously established words.
- If there is no word to be installed, it rolls back to the last word intersecting with it, the search for which continues as if its previous value was not found at all.
Checked - it really works on the grids to the average level of complexity. However, as the crossword grid becomes more complex and the number of words increases, the number of successful attempts at generation tends to 0. Actually, from this moment the most interesting begins.
Templates
The first question that comes to mind is it possible to somehow reduce the number of kickbacks? After all, each rollback to a few words back can cost tens and hundreds of thousands of iterations. The logical step is to add rules that reduce the number of mistakes in the installation of words, like, do not put a soft or hard sign in the cell where the word begins, etc. If you don’t crawl deeply, it’s quite simple to describe most of these rules for the Russian language, but there is a problem - they will be absolutely useless, for example, for English. I also wanted to make a universal algorithm that does not depend on the language.
Reflections on this issue led to the following: “it would be good if for every unspecified word that crosses the currently installed word, the availability of options for the installation is guaranteed”.
So the idea was to use templates like the LIKE command in Transact-SQL. A pattern is a character string by which words will be compared. The template itself includes letters and template characters. During the comparison with the template, it is necessary that the letters exactly match the characters specified in the string. Template characters can match arbitrary elements of a character string.
Decision number 5: For each starting word, patterns of all words intersecting with it will be calculated. The starting word must have letters strictly from the list in the template corresponding to the position of the letter of the intersection. This solution is used at the generation stage.
Examples of patterns for words of three letters are given below:
- Template: "___"
- Letter number 1: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
- Letter № 2: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
- Letter number 3: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
- Template: "TO_"
- Letter number 1: D
- Letter number 2: O
- Letter № 3:
On the example of the latter, the patterns should be read as follows: for a word of 3 letters, whose first two letters are equal to “BEFORE”, there are words in the database that have the last letter equal to one of “KMN”.
Accelerators
Let's go back to the fragments. Look at the picture below.

In it, the cells of the words set earlier are marked in gray. When you install the word marked in red, two fragments are formed at once, marked with blue and purple flowers.
If you look at the purple fragment, you will see that it is associated with the starting word with one single intersection. And it is beautiful! This gives us the opportunity to use another solution.
Some more terminology:
- Accelerator is a start word with a child fragment, having only one intersection with it. It received its name for the property to accelerate the generation of fragments by an order of magnitude or more.
Solution # 6: If a fragment is unsuccessful, for which the starting word is an accelerator, the algorithm will store a list of letters that were set to the starting word at the intersection with one of the words of the fragment to block repeated settings of words that have these letters on the intersection. This solution is used at the generation stage.
The algorithm for using accelerators is given below.
First, how it works without an accelerator:
- Searches and installs all words in a fragment.
- If the filling of the fragment is completed successfully, then go ahead, otherwise, the starting word changes and the process of filling in the words of the fragment is repeated.
The fragment depth can be quite large, and the total number of iterations to fill a fragment can be in the millions. To iterate over all possible options, you need the number of iterations for a single filling of the fragment, multiplied by the number of words in the database with a length, like a starting word (of which there may be tens of thousands).
How it works with the accelerator:
- Searches and installs words for a fragment.
- If the fragment is completed successfully, then go ahead, otherwise, we remember the letter that stands at the intersection of the accelerator and the word of the fragment.
- The word set on the accelerator changes, and the new word should not have letters that were previously memorized at the above-mentioned intersection.
The depth of the fragment is the same. However, to iterate over all possible options, you need to multiply the number of iterations to fill a fragment not by the number of options for the start word, but by only 33 (the number of letters in the alphabet).
Dynamic balancing installation complexity
The previous decisions have essentially exhausted the 20% of efforts that, according to the Pareto principle, give us 80% of the result. Further, it is necessary to use more and more complex approaches, with sometimes unclear prospects.
Once, when generating a crossword puzzle, the program gave the following message: “Bust time: 11,471 days ...”. This message appears only if all the variants were searched for the very first word and you need to find a new value for it. The program has already spent time simply multiplies by the remaining number of options. It amused me and made me wonder if this time could be converted into a result? The idea is to deliberately cut off some brute force options that have a minimal likelihood of success.
The main thesis of this decision is that even better the program will produce a negative result in the shortest possible time (i.e., among the most optimal options, selection failed) than it will be in selection so much time that all conceivable limits will be exceeded.
Decision number 7: When installing a word that intersects words with great complexity of installation, it is forbidden to put the letters in the position of the intersection, the frequency of which is used in words of intersections is minimal. This solution is used at the generation stage.
If simple, this solution discards a certain number of letters of the Russian alphabet (sometimes up to 20), increasing the chance to generate complex sections of words with the most frequently used letters (here in chocolate the Italian alphabet with its 21 letters). As a result, we will get more options for the selection of difficult to install words, when it comes to the turn, which means more chance for successful generation of the whole crossword puzzle.
There are also disadvantages - some of the brute force options will be irretrievably lost. Perhaps among them will be the one, the only possible option to fill the grid. Only you can get it in 30 years - you just need to wait a bit.
Another disadvantage is that long words with more than 10 intersections are blocked the most. This leads to the fact that the program can not start generation, blocking the first word, until the options for it end. This minus is only partially managed by reducing the degree of blocking, and hence the effectiveness of this solution.
Testing
To systematize grids by generation complexity, the attribute “Generation complexity” is introduced, which is calculated based on the number of words, their length, and the number of intersections. In fact - more or less stable result can be obtained with the complexity of up to 600 units. All that is higher - for good luck.
Below is shown the average generation time for 10 attempts for several grids arranged in order of increasing complexity of generation.
Grid number 1

Simple test grid for experiences, with a small amount of words.
- Generation complexity: 248
- Number of words: 28
- Average time of successful generation, sec .: 5 (from 1 to 32)
Subtotal: Grids of such complexity are generated quickly and stably.
Grid number 2

This grid is more complicated. This is a small “Canadian” crossword puzzle, where all words have intersections on all letters.
- Generation complexity: 372
- Number of words: 34
- Average time of successful generation, sec .: 62 (from 1 to 472)
Subtotal: Grids of such complexity in most cases are generated fairly quickly, however, sometimes the generation can take 10 minutes or more.
Grid number 3

This rather complicated grid turned out to be quite “convenient” for generation.
- Generation complexity: 544
- Number of words: 46
- Average time of successful generation, sec .: 1 (from 1 to 2)
Subtotal: Due to the fact that this grid is very well fragmented and intersections are not available on all letters of long words, the program generates it almost instantly.
Grid number 4

But this grid already has a “target” complexity. This is a full-fledged "Canadian" crossword, though not the most difficult one.
- Generation complexity: 570
- Number of words: 78
- Average time of successful generation, sec .: 250 (from 10 to 989)
Subtotal: The program handled! A successful generation result, at the very least, can be obtained in just 17 minutes. The average generation time is just over 4 minutes.
Grid number 5

And finally - the most difficult crossword puzzle that started it all. It has 72 words, which is not so much. However, the complexity of the generation was very high. The main problem for generation are the four longest words with which almost all other words of the crossword cross. They are like bones of the skeleton, on which you need to strung all the other words. Kickbacks discard the generation process almost to the very beginning. Thus, the process of generating this grid can be compared with Sisyphus, pushing a stone up the hill. And every time there is very little to the goal, the stone rolls to the very beginning of the path.
Alas - this peak has remained unconquered! I ran several generations with different settings, with a limit of up to 10 hours in duration, but none of them was completed successfully. Time is clearly not enough. Who knows, maybe this unconquered peak will inspire someone for a new assault!
Summary
And yet yes! Generating a crossword puzzle, even for the most modern computers, is a difficult task. I am sure that the possibilities to improve this algorithm are far from exhausted, however, regardless of the capabilities of the algorithm and the power of the computer, you can always complicate the crossword grid a little more so that the program promises you a result in 20-30 years.
I hope you were interested, and you read to the end.
Source: https://habr.com/ru/post/249899/
All Articles