PARI / GP: finite field calculations. Part 1

Why PARI / GP?

PARI / GP is a computer-mathematics system with its own C-like interpreted language, focused on computational number theory. The system is popular in the scientific community: according to Google Scholar, in 2014 alone, about 100 topical articles using PARI / GP were published in refereed journals / conferences.

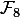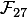In my dissertation research, I often needed to solve the traditional problems of linear algebra (for example, for a matrix of large dimension to calculate its core and rank), but only over finite fields (for example, or ). If we had just complex matrices, then all at least some well-known systems of symbolic mathematics would cope effectively: for example, in my favorite Wolfram Mathematica, it suffices to use the NullSpace and MatrixRank functions, respectively. It would be great if the same functions were once earned for matrices over finite fields, albeit with a loss in performance due to the inefficiency of the general linear algebra algorithms for them ... Alas, I got an exponential growth (up to hours on my poor netopovy laptop ) computation time from the dimension of matrices (see my question on the Wolfram Mathematica profile forum). True, in fairness, this was caused not so much by the problems of implementing algorithms for linear algebra as by the problems of the symbolic processor itself.

To my great joy, PARI / GP is intended for calculations in various algebraic systems (rings, fields), operating with their elements as “atomic” numbers, and not as symbolic structures over built-in types. According to my empirical observation, PARI / GP has an unsurpassed speed of such calculations. In addition, there is the possibility of translating the interpreted code into pure C.

Basic functions for working in final fields

The description below is rather “high-level”, without reference to the algorithms and data structures used within PARI / GP (topics of future posts).

• The function ffinit (q, n, {v}) computes the normalized irreducible over a simple field a polynomial f (v) of degree n in the variable v (optional, the default is the polynomial of argument x). For example: calling ffinit (2, 3, x) returns a primitive polynomial 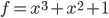, and ffinit (2, 4, x) is simply an irreducible polynomial . Now we can set the extension 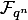finite field classically as a factor ring .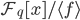
• Root 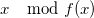an irreducible polynomial f (x) as a PARI / GP object is created using the ffgen (f, x) function. In other words, the call g = ffgen (f, x) returns the object g, identified with the equivalence class [x] - element of the factor ring 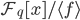. Now field 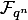considered as linear space over , it is possible to construct (its tables of addition and multiplication) with the help of the generating set .
• You can find a primitive field element using the ffprimroot (g) function. This function calculates a random element of order (n - 1) in the multiplicative group of a finite field, which is given by the object g.
• Using the minpoly (a) function, we can find the minimal polynomial of the element a of a finite field. For example, calling p = minpoly (a) will return . In other words, finding a primitive field element 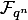field can be represented in the traditional form where p is its primitive polynomial.

')

Life example

Preliminary reference

As already mentioned, PARI / GP uses its C-like language. A detailed guide can be found here . The following is a brief description explaining some points of the example below (and even more):

1. All objects in PARI / GP are created on its internal stack. By default, the internal stack occupies 3.8MB (4 million bytes) of computer dynamic memory. To expand it, use the allocatemem (s) function, where s is the requested number of bytes.
2. Separator ";" at the end of the line is used to prohibit the printing of the result.
3. By default, any identifier is a variable for polynomials. You can use an apostrophe in front of the identifier, which indicates that it is a variable for polynomials, and not an object. For example,
   

   x = 12; type(x) >"t_INT" type('x) >"t_POL" 

   
   
4. The curly brackets "{", "}" are used only for grouping commands (for example, multi-line). Grouping does not specify the scope (life) of any object declared inside it. By default, all declared variables are global. For an object to become locally bound, it must be declared using the my specifier. For example,
   

    { x = 12; } x >12 { my(y = -13.2); } y >y 

   
   
5. PARI / GP allows the user to create lambda functions. The syntax is as follows: lambda = (argument list) -> function body;

Example itself

 createField = (q, n, var) -> ffgen(minpoly(ffprimroot(ffgen(ffinit(q, n, var), var))), var); a = createField(2, 4, 'x) >x fforder(a) \\     >15 allocatemem(2^27); \\  128     PARI/GP M = matrix(1000, 1000, i,j, random(a)); \\   10001000    GF(16) {gettime(); matrank(M); gettime()} \\   ()      >34209 {gettime(); kernel(M~); gettime()} \\         >88425 

The configuration of my laptop is Intel Core (TM) i7-4702M CPU @ 2.20GHz 2.20GHz, 32kB L1 cache, 8Gb DDR3. PARI / GP 2.7.2 (32bit, single thread) was used - this is the last out of the box release of this text under Windows OS.