To recognize the pictures, you do not need to recognize the pictures.
Look at this photo.

This is a completely ordinary picture, found in Google on request "railway". And the road itself is also nothing special.
')
What happens if you remove this photo and ask you to draw a railroad from memory?
If you are a child of seven years old, and have never learned to draw before, it is very likely that you will have something like this:
Oops. It seems that something went wrong.
Let's go back to the rails on the first picture and try to understand what is wrong.
In fact, if you look at it for a long time, it becomes clear that it does not exactly reflect the world around it. The main problem about which we immediately stumbled - there, for example, parallel straight lines intersect. A series of identical (in reality) lampposts is in fact depicted in such a way that each successive pillar has smaller and smaller dimensions. The trees around the road, in which individual branches and leaves are first distinguishable, merge into a solid background, which for some reason also acquires a distinctly purple hue.
All of these are perspective effects, the consequences of the fact that three-dimensional objects are projected outside on a two-dimensional retina inside the eye. There is nothing magically separate about this - just a little curious why these distortions of contours and lines do not cause us any problems with orientation in space, but suddenly cause the brain to tense up when trying to take up a pencil.
Another great example is how little children paint the sky.

The sky should be at the top - here it is, a blue stripe pinned to the top edge. At the same time, the middle of the leaf remains white, filled with the emptiness in which the sun floats.
And so it happens always and everywhere. We know that a cube consists of square faces, but look at the picture , and you will not see a single right angle there - moreover, these angles are constantly changing, it is worth changing the viewing angle. It is as if somewhere in our head a rough outline of a regular, three-dimensional object is preserved, and it is to her that we turn in the process of drawing the rail, not immediately managing to compare the result with what we see with our own eyes.
In fact, it is still worse. How, for example, in the very first picture of the road, we determine which part of the road is located closer to us, and which further? As you remove objects become smaller, ok - but are you sure that someone has not deceived you, slyly placing one after another successively decreasing sleepers? Distant objects usually have a pale bluish tint (an effect called “atmospheric perspective”) - but the subject may simply be painted in that color, and otherwise appear completely normal. The bridge over the railroad tracks, which can hardly be seen from here, seems to be behind us, because it is obscured by lights (the effect of occlusion) - but again, how can you be sure that the lights are not painted on its surface? This whole set of rules, with the help of which you evaluate the three-dimensionality of the scene, depends largely on your experience, and perhaps the genetic experience of your ancestors, who are trained to survive in our atmosphere, the light falling from above and the flat horizon.
By itself, without the help of a powerful analytical program in your head filled with this visual experience, any photo speaks of the world around you terribly little. Images are rather such triggers that make you mentally imagine a scene, much of the knowledge about which you already have in mind. They do not contain real objects - only limited, flattened, tragically two-dimensional ideas about them, which, moreover, are constantly changing when moving. In some ways, we are the same people in Flatland, who can see the world only from one side and inevitably distorted.
Imagine that you are a neural network.
It doesn't have to be very difficult — after all, somehow it really is. You spend your free time recognizing people on documents in the passport office. You are a very good neural network, and your work is not too complicated, because in the process you are guided by a pattern that is strictly characteristic of human faces - the relative position of two eyes, nose and mouth. The eyes and noses themselves may differ, some one of the signs may sometimes be indistinguishable in a photograph, but the presence of others always helps. And suddenly you come across this:

Hmm, you think. You definitely see something familiar — at least in the center there seems to be one eye. True, a strange form - it looks like a triangle, and not a pointed oval. The second eye is not visible. The nose, which should be located in the middle and between the eyes, went somewhere completely to the edge of the contour, and you could not find a mouth at all - definitely, a dark corner from the bottom-left does not look like it at all. Do not face - you decide, and throw the picture in the trash.
So we would think if our visual system was engaged in a simple comparison of patterns in images. Fortunately, she thinks somehow differently. The absence of a second eye does not cause any concern to us; this makes the face no less resembling a face. We mentally pretend that the second eye should be on the other side, and its shape is due solely to the fact that the head in the photo is turned and looks to the side. It seems impossible to be trivial when you try to explain it in words, but some of you would seriously disagree with you.
The most annoying thing is that you cannot see how this question can be solved mechanically. Computer vision has been confronted with the relevant problems for a very long time, since its inception, and periodically found effective private solutions - so, we can identify a subject that has been moved to the side, consistently moving our test pattern across the entire image (which convolution networks use successfully), we can cope with scaled or rotated pictures using SIFT, SURF and ORB signs, but the effects of perspective and the rotation of an object in the scene space seem to be of a qualitatively different level. Here we need to know how the object looks from all sides , to get its true three-dimensional shape, otherwise we have nothing to work with. Therefore, to recognize the pictures, you do not need to recognize the pictures . They are false, deceptive and obviously inferior. They are not our friends.
So, the important question is how do we get a three-dimensional model of everything we see? An even more important question is how to do without the need to buy a laser spatial scanner (at first I wrote “damn expensive laser scanner”, and then came across this post )? Even not so much for the reason that we are sorry, but because the animals in the process of evolution of the visual system obviously somehow did without it, only with their eyes, and it would be curious to find out how they are.
Somewhere in this place, a part of the audience usually gets up and leaves the hall, cursing for marking time - everyone knows that we use binocular vision to perceive depth and space, we have two special eyes for this! If you think so too, I have a little surprise for you - this is not true. The proof is beautiful in its simplicity - just close one eye and walk around the room to make sure that the world has not suddenly lost its depth and does not look like a flat analogue of an animated cartoon. Another way is to go back and look at the photo with the railroad again, where the depth can be clearly seen even though it is located on a completely flat monitor surface.
So, binocular vision does not suit us - and with it we reject stereo cameras, range finders and Kinect. Whatever the ability of our visual system to recreate three-dimensional images of the seen, it clearly does not require two eyes. What remains in the end?
I am by no means ready to give an exact answer in relation to biological vision, but perhaps, for the case of an abstract robot with a camera instead of an eye, there is one promising way. And this way is movement.
Back to the train theme, only this time we look out the window:

What we see at the same time is called “motion parallax”, and in short it lies in the fact that when we move sideways, close objects shift into the field of view more than distant ones. For moving forward / backward and turning, we can also formulate the relevant rules, but let's ignore them for now. So, we are going to move, assess the displacements of objects in the frame and on the basis of this, determine their distance from the observer - a technique that is officially called “structure-from-motion”. Let's try.
First of all - have they done everything, by chance, before us? The “Structure from motion” page on Wikipedia offers as many as thirteen tools (and these are only open source) for recreating 3D models from a video or a set of photos, most of them use an approach called bundle adjustment, and the most convenient one seemed to me Bundler (and demo he is cool). Unfortunately, there is a problem that we still face - the Bundler wants to know the camera model and its internal parameters from us (as a last resort, if the model is unknown, it requires you to specify the focal length).
If this is not a problem for your task, you can safely stop reading, because this is the simplest and at the same time effective method (do you know, by the way, what were the models used in the game “The Disappearance of Ethan Carter” ?). For me, alas, the need to be tied to a camera model is a condition that I would very much like to avoid. Firstly, because we have a full YouTube visual video experience that we would like to use in the future as a sample. Secondly (and this may be even more important), because our human brain, it seems, if it knows in numbers the internal parameters of the camera of our eyes, it is perfectly able to adapt to any optical distortion. Looking through the lens of a wide-focus camera, fishing, watching movies and wearing oculus does not completely destroy your visual abilities. So, probably, some other way is possible.
So, we sadly closed the pagewith Itan Carter of Wikipedia and go down to the level below - in OpenCV, where we are offered the following:
1. Take two shots taken from a calibrated camera.
2. Together with the calibration parameters (camera matrix), put them both into the stereoRectify function, which rectifies these two frames - this is a transformation that distorts the image so that the point and its displacement are on the same horizontal line.
3. We put these rectified frames into the stereoBM function and get a disparity map — such a picture in shades of gray, where the pixel is brighter, the more displacement it expresses (there is an example by reference).
4. Put the resulting displacement map into a function with the speaker name reprojectImageTo3D (we will also need the Q matrix, which we will receive among others in step 2). We get our three-dimensional result.
Hell, it looks like we are stepping on the same rake - in paragraph 1 we are required to use a calibrated camera (although OpenCV graciously gives us the opportunity to do it ourselves). But hey, here's a plan. B. In the documentation, there is a function with the suspicious name stereoRectifyUncalibrated ...
Plan b:
1. We need to estimate the approximate part of the displacements by ourselves - at least for a limited set of points. StereoBM is not suitable here, so we need some other way. A logical option would be to use feature matching - find some special points in both frames and select mappings. About how this is done, you can read here .
2. When we have two sets of matching points, we can throw them into findFundamentalMat to get the fundamental matrix that we need for stereoRectifyUncalibrated.
3. Run stereoRectifyUncalibrated, we get two matrices for rectifying both frames.
4. And ... and then it is not clear. We have rectified frames, but there is no Q matrix, which was needed for the final step. Googling, I came across about the same perplexity of the post , and realized that I either missed something in theory, or did not think about this moment in OpenCV.
OpenCV: we are 2-0.
But wait. Perhaps, from the very beginning, we didn’t go the wrong way. In previous attempts, we, in fact, tried to determine the real position of three-dimensional points - hence the need to know the parameters of the camera, the matrix, rectify frames, and so on. In fact, this is the usual triangulation: on the first camera I see this point here, and on the second here - then we draw two rays passing through the centers of the cameras, and their intersection will show how far the point is from us.
This is all fine, but generally speaking, we do not need it. The real sizes of objects would interest us if our model would be used later for industrial purposes, in some 3d-printers. But we are going (this goal has already spread slightly, really) to push the data into the neural network and similar classifiers. For this we need only know the relative sizes of objects. They, as we still remember, are inversely proportional to the parallax displacements - the farther the object is from us, the less it shifts during our movement. Is it possible to somehow find these offsets even easier, simply by somehow matching both pictures?
Of course, you can. Hi, optical flow .
This is a great algorithm that does exactly what we need. Put in it a picture and a set of points. Then we put the second picture. We get at the output for given points their new position in the second picture (approximate, of course). No calibrations and no mention of the camera at all - the optical flow, despite the name, can be calculated on the basis of anything. Although usually it is still used for tracking objects, collision detection, and even augmented reality .
For our purposes, we (for the time being) want to use Gunnar Farnebak's “dense” flow, because he can calculate the flow not for any particular points, but for the whole picture at once. The method is available using calcOpticalFlowFarneback, and the very first results are beginning to be very, very good - see how much it looks cooler than the previous result stereoRectifyUncalibrated + stereoBM.

Many thanks to the great game Portal 2 for the opportunity to build your own rooms and play cubes. I'm doin 'Science!
So, great. We have displacements, and they look quite good. How now do we get from them the coordinates of three-dimensional points?
This picture is already flashed on one of the links above.
The distance to the object is calculated here using the school geometry method (similar triangles), and it looks like this: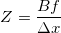 . And the coordinates, respectively, like this:
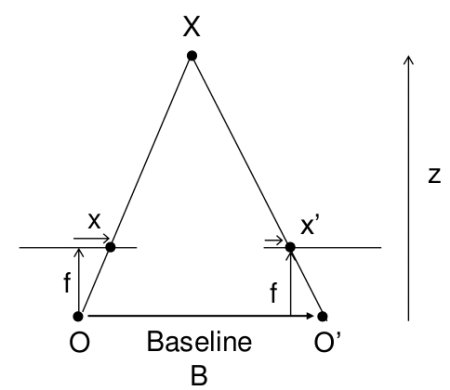
. And the coordinates, respectively, like this: 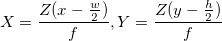 . Here, w and h are the width and height of the image, they are known to us, f is the focal length of the camera (the distance from the center of the camera to the surface of its screen), and B is the same pitch. By the way, please note that we slightly violate the generally accepted names of the axes here, when Z is directed upwards - we have Z looking at the depth of the screen, and X and Y - respectively, are directed along the width and height of the picture.
. Here, w and h are the width and height of the image, they are known to us, f is the focal length of the camera (the distance from the center of the camera to the surface of its screen), and B is the same pitch. By the way, please note that we slightly violate the generally accepted names of the axes here, when Z is directed upwards - we have Z looking at the depth of the screen, and X and Y - respectively, are directed along the width and height of the picture.
Well, everything is simple about f - we have already stipulated that the real parameters of the camera do not interest us, if only the proportions of all the objects would change according to one law. If we substitute Z into the formula for X above, then we can see that X doesn’t depend on focal length at all (f is reduced), so its different values will change only the depth - “stretch” or “flatten” our scene. Visually, it is not very pleasant, but again, for the classification algorithm, it doesn’t matter anyway. So let's set the focal length in an intelligent way - just think of it. I, however, reserve the right to slightly change the opinion further in the text.
About B is a bit more complicated - if we don’t have a built-in pedometer, we don’t know what distance the camera has moved in the real world. So let's think a little while and decide that the camera movement is approximately smooth, we have a lot of frames (a couple of tens per second), and the distance between two neighboring ones is about the same, i.e. . And again, then we will slightly clarify this situation, but for now let it be so.
. And again, then we will slightly clarify this situation, but for now let it be so.
Here is the result. I hope this gif has time to load while you read this far.
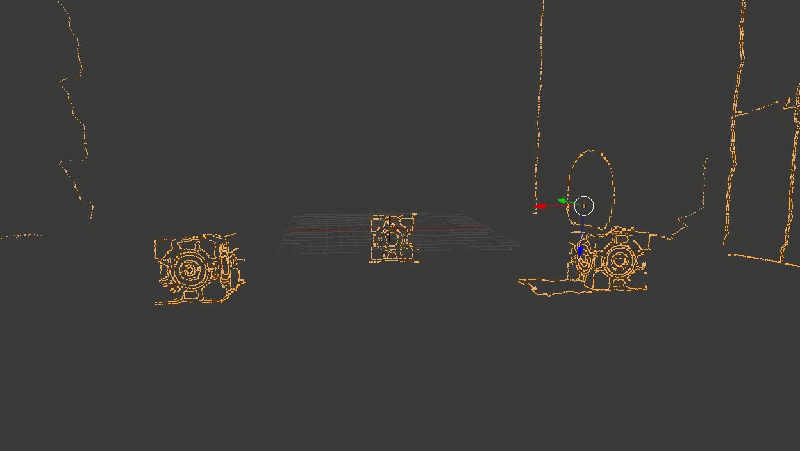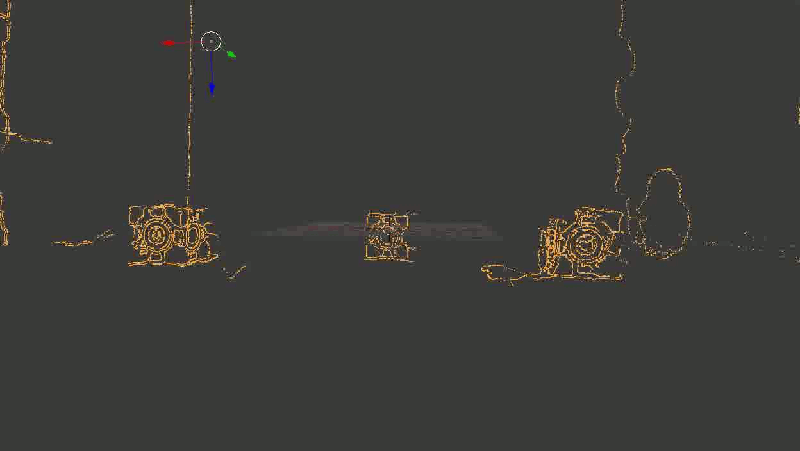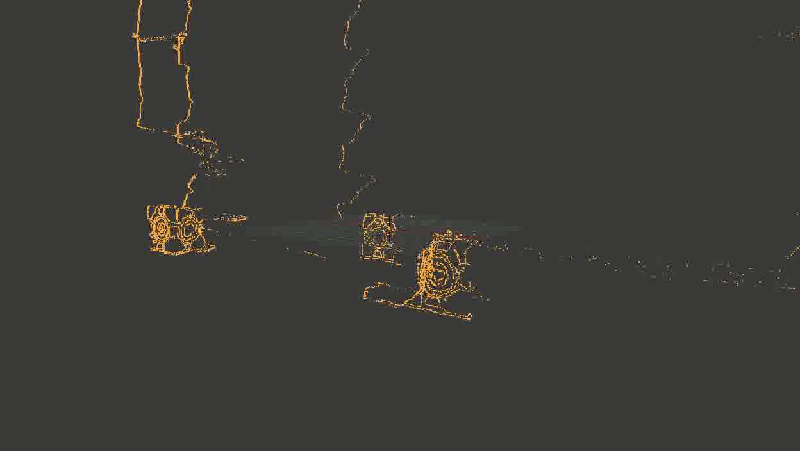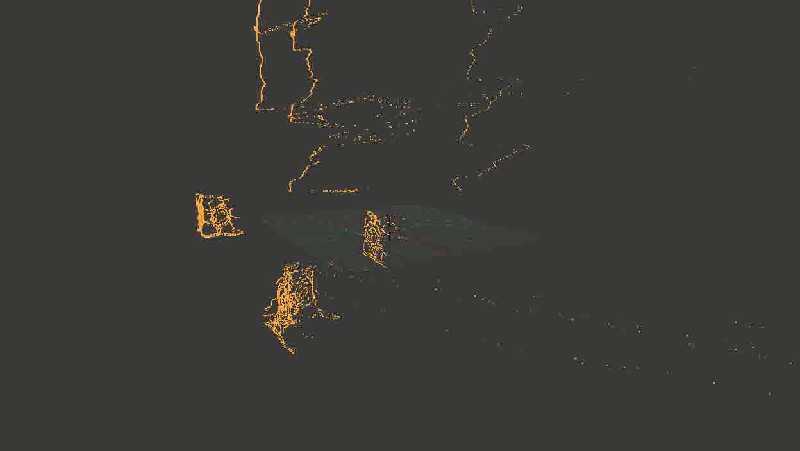
For clarity, I took not all points in a row, but only the borders highlighted by the Canny-detector
At first glance (in any case, to me) everything seemed to be excellent - even the angles between the faces of the cubes formed pretty ninety degrees. The objects in the background got worse (notice how the contours of the walls and the door were distorted), but hey, it's probably just a little noise, it can be cured using more frames or anything else.
Of all the possible hasty conclusions that could be made here, this turned out to be the furthest from the truth.
In general, the main problem was that some of the points were rather distorted. And - an alarming sign, where it was time to suspect that something was wrong - was distorted not in a random way, but approximately in the same places, so it was impossible to correct the problem by successively superimposing new points (from other frames).
I tried to fix it for a very long time, and during that time I tried the following:
- smooth karinka with optical flow: blur according to Gauss, median filter and a fancy bilateral filter that leaves clear edges. It is useless: objects on the contrary, blurred even more.
- tried to find straight lines in the picture with the help of Hough transform and move them in the same direct state. Partly worked, but only on the borders - the surface still remained the same distorted; plus it was impossible to put a thought in the spirit of “what if there are no straight lines in the picture at all”.
- I even tried to make my own version of the optical stream, using OpenCV templateMatching. It worked like this: for any point we build a small (about 10x10) square around it, and we start moving it around and looking for the maximum match (if the direction of movement is known, then we can limit it around). It turned out quite well in places (although it worked clearly slower than the original version):

On the left is the familiar Farnebak stream, on the right is the above described bike.
In terms of noise, alas, it turned out no better.
In general, everything was bad, but very logical. Because it should be so.
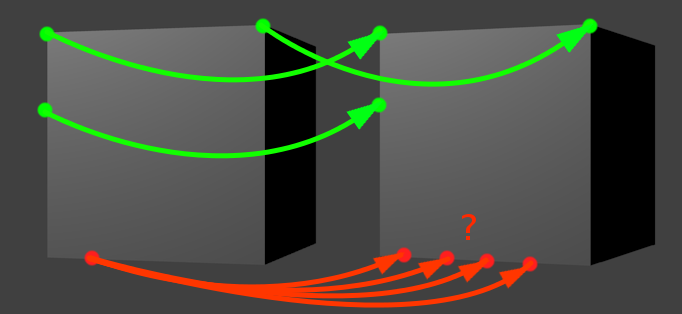
Illustration to the problem. Moving here is still a step to the right.
Let's pick some green dot from the image above. Suppose we know the direction of motion, and are going to look for the “displaced twin” of our green point, moving in a given direction. When do we decide that we have found the desired twin? When we stumble upon some kind of “landmark”, a characteristic site that is similar to the environment of our starting point. For example, on the corner. The angles in this respect are easy to track, because they themselves are quite rare. Therefore, if our green point is an angle, and we find a similar angle in a given neighborhood, then the problem is solved.
The situation with the vertical line (the second left green dot) is slightly more complicated, but still easy. Considering that we are moving to the right, we will meet the vertical line only once for the entire search period. Imagine that we are crawling with our search window in the picture and see a monophonic background, background, again a background, a vertical segment, again a background, a background, and again a background. Also easy.
The problem occurs when we try to track a piece of the line parallel to the movement . The red dot does not have one clearly pronounced candidate for the role of a displaced twin. There are many of them, they are all close by, and it’s simply impossible to choose any one method we use. This is a functional limitation of the optical flow. As Wikipedia kindly warns us in the relevant article, "We cannot solve this problem, and there is nothing to be done.
In fact, as late common sense prompts at this point, we are still trying to do extra work that is not important for our ultimate goal — recognition, classification, and other intelligence. Why are we trying to cram all the points in the 3D world? Even when we work with two-dimensional images, we usually do not try to use each pixel for classification - most of them do not carry any useful information. Why not do the same here?
Actually, everything turned out just like that. We will calculate the same optical flow, but only for green, stable points. And by the way, in OpenCV we have already been taken care of. The thing we need is called the Lucas-Canada stream.
It will be a bit boring to give the code and examples for the same cases, because you get the same thing, but with a much smaller number of points. On the way, let's do something else: for example, let's add the ability to process camera turns to our algorithm. Before that, we were moving exclusively sideways, which is quite rare in the real world outside of train windows.
With the advent of turns, the coordinates of X and Z are mixed together. Let's leave the old formulas for calculating coordinates relative to the camera, and we will translate them into absolute coordinates as follows (here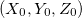 - coordinates of the camera position, alpha - angle of rotation):
- coordinates of the camera position, alpha - angle of rotation):
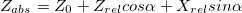
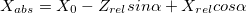

(cheater; it's because we think the camera doesn't move up and down)
Somewhere here we have problems with focal length - remember, we decided to set it arbitrary? So, now, when we had the opportunity to estimate the same point from different angles, it began to matter - precisely because the coordinates X and Z began to interfere with each other. In fact, if we run a code similar to the previous one, with an arbitrary focus, we will see something like this:

It is not obvious, but it is an attempt to arrange a camera bypass around a regular cube. Each frame - evaluation of visible points after the next rotation of the camera. Top view, as on the minimap.
Fortunately, we still have an optical stream. When turning, we can see which points pass into which, and calculate the coordinates for them from two angles. From here, it’s easy to get the focal length (just take the two formulas above for different alpha values, equate the coordinates and express f). So much better:
Not that all points would lie ideally one into another, but you can at least guess that this is a cube.
And finally, we need to somehow deal with the noise due to which our estimates of the position of points do not always coincide (see on the top of the hypha neat uneven ringlets? Instead of each of them, ideally, there should be one point). There is already room for creativity, but the most adequate way seemed to me like this:
- when we have several shifts to the side in a row, we combine information from them together - so for one point we will have several depth estimates at once;
- when the camera rotates, we try to combine two sets of points (before turning and after) and adjust one to the other. This fitting is correctly called “registration of points” (which you would never have guessed when hearing the term in isolation from the context), and for it I used the Iterative closest point algorithm to download the version for python + OpenCV;
- then the points that lie within the threshold radius (determined by the method of the nearest neighbor) merge together. For each point, we still track something like “intensity” - a counter of how often it was combined with other points. The greater the intensity - the greater the chance that this is an honest and correct point.
The result may not be as solid as in the case of cubes from the Portal, but at least, it is exact. Here are a couple of recreated models that I first uploaded to Blender, twirled the camera around them and saved the resulting footage:
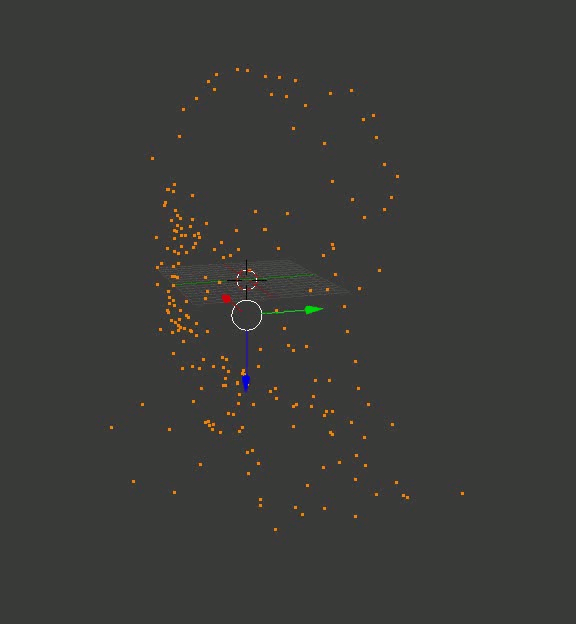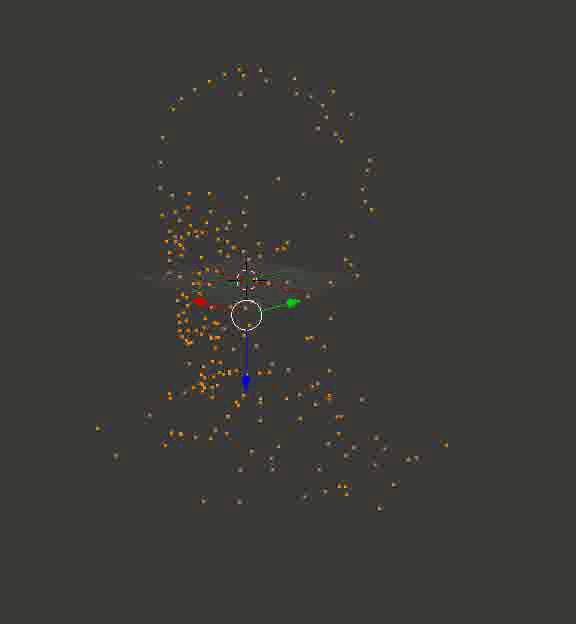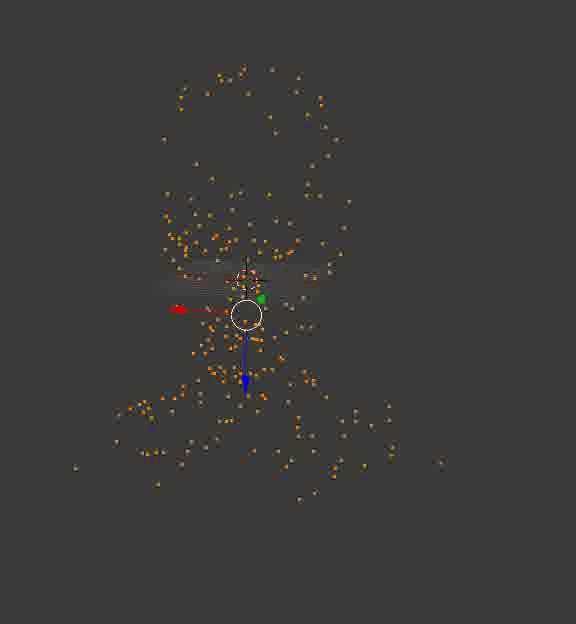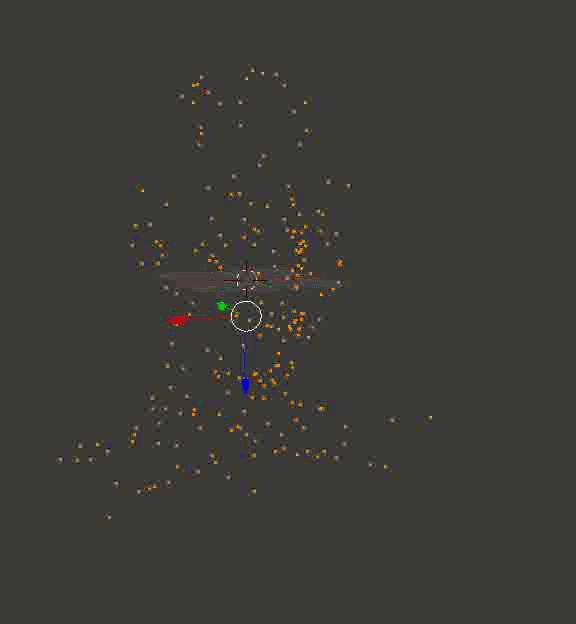
Professor Dowell's Head

Some random machine
Bingo! Then you need to push them all into the recognition algorithm and see what happens. But it, perhaps, we will leave on the following series.
Let's look back a little and remember why we all did it. The line of reasoning was:
- we need to be able to recognize the things depicted in the pictures
- but these pictures change every time when we change position or look at the same thing from different angles. Sometimes unrecognizable
- this is not a bug, but a feature: due to the fact that our limited eye sensors see only a part of the object, and not the entire object
- therefore, it is necessary to somehow combine these partial data from the sensors and collect from them the idea of the subject in its full form.
Generally speaking, this is certainly not just a problem of sight. This is rather a rule, not an exception - our sensors are not omnipotent, they constantly perceive information about an object in parts - but it is curious how all such cases can be combined into some common framework? Say (returning to vision), your eyes are now constantly making small and very fast movements - saccades - jumping between objects in sight (and in the intervals between these movements your vision does not work at all - that is why you cannot see your own saccades, even when you stare at the mirror point blank). The brain is constantly engaged in hard work on the "stitching" of the pieces. Is this the same task that we just tried to solve, or is it another? Perception of speech, when we can relate a dozen different variants of the pronunciation of a word with one of its “ideal” spelling - is this a similar task too? What about the reduction of synonyms to one "image" of the subject?
If so, then perhaps the problem is somewhat more than just a parietal algorithm of the visual system, which replaces the laser pointer of the scanner with our under-evolved eyes.
Obvious considerations say that when we try to recreate some thing seen in nature, there is no point in blindly copying all its constituent parts. To fly through the air, waving wings and feathers are not needed, a stiff wing and lift are sufficient; To run fast, you do not need mechanical legs - the wheel will cope much better. Instead of copying what we saw, we want to find a principle and repeat it on our own (maybe, making it easier / more efficient). What is the principle of intelligence, an analogue of the laws of aerodynamics for flight, we do not yet know. Deep learning and Yan Lekun, his prophet (and many other people following him) believe that one should look towards the ability to build "deep" hierarchies of features from the data obtained. Maybe we can add to this one more clarification - the ability to combine together relevant pieces of data, perceiving them as parts of one object and placing them in a new dimension?

This is a completely ordinary picture, found in Google on request "railway". And the road itself is also nothing special.
')
What happens if you remove this photo and ask you to draw a railroad from memory?
If you are a child of seven years old, and have never learned to draw before, it is very likely that you will have something like this:
Oops. It seems that something went wrong.
1. The strange way we see things
Let's go back to the rails on the first picture and try to understand what is wrong.
In fact, if you look at it for a long time, it becomes clear that it does not exactly reflect the world around it. The main problem about which we immediately stumbled - there, for example, parallel straight lines intersect. A series of identical (in reality) lampposts is in fact depicted in such a way that each successive pillar has smaller and smaller dimensions. The trees around the road, in which individual branches and leaves are first distinguishable, merge into a solid background, which for some reason also acquires a distinctly purple hue.
All of these are perspective effects, the consequences of the fact that three-dimensional objects are projected outside on a two-dimensional retina inside the eye. There is nothing magically separate about this - just a little curious why these distortions of contours and lines do not cause us any problems with orientation in space, but suddenly cause the brain to tense up when trying to take up a pencil.
Another great example is how little children paint the sky.

The sky should be at the top - here it is, a blue stripe pinned to the top edge. At the same time, the middle of the leaf remains white, filled with the emptiness in which the sun floats.
And so it happens always and everywhere. We know that a cube consists of square faces, but look at the picture , and you will not see a single right angle there - moreover, these angles are constantly changing, it is worth changing the viewing angle. It is as if somewhere in our head a rough outline of a regular, three-dimensional object is preserved, and it is to her that we turn in the process of drawing the rail, not immediately managing to compare the result with what we see with our own eyes.
In fact, it is still worse. How, for example, in the very first picture of the road, we determine which part of the road is located closer to us, and which further? As you remove objects become smaller, ok - but are you sure that someone has not deceived you, slyly placing one after another successively decreasing sleepers? Distant objects usually have a pale bluish tint (an effect called “atmospheric perspective”) - but the subject may simply be painted in that color, and otherwise appear completely normal. The bridge over the railroad tracks, which can hardly be seen from here, seems to be behind us, because it is obscured by lights (the effect of occlusion) - but again, how can you be sure that the lights are not painted on its surface? This whole set of rules, with the help of which you evaluate the three-dimensionality of the scene, depends largely on your experience, and perhaps the genetic experience of your ancestors, who are trained to survive in our atmosphere, the light falling from above and the flat horizon.
By itself, without the help of a powerful analytical program in your head filled with this visual experience, any photo speaks of the world around you terribly little. Images are rather such triggers that make you mentally imagine a scene, much of the knowledge about which you already have in mind. They do not contain real objects - only limited, flattened, tragically two-dimensional ideas about them, which, moreover, are constantly changing when moving. In some ways, we are the same people in Flatland, who can see the world only from one side and inevitably distorted.
more perspective
In general, the world around is full of evidence of how perspective distorts everything. People supporting the Tower of Pisa, photographs with the sun in their hands, not to mention Escher’s classic paintings, or a perfect example of this - the Ames Room . Here it is important to understand that these are not some isolated tricks, specially made to deceive. The prospect always shows us a defective picture, just as a rule, we are able to “decode” it. Try to look out the window and think that what you see is deception, distortion, hopeless inferiority.
2. Images are not real, Neo
Imagine that you are a neural network.
It doesn't have to be very difficult — after all, somehow it really is. You spend your free time recognizing people on documents in the passport office. You are a very good neural network, and your work is not too complicated, because in the process you are guided by a pattern that is strictly characteristic of human faces - the relative position of two eyes, nose and mouth. The eyes and noses themselves may differ, some one of the signs may sometimes be indistinguishable in a photograph, but the presence of others always helps. And suddenly you come across this:

Hmm, you think. You definitely see something familiar — at least in the center there seems to be one eye. True, a strange form - it looks like a triangle, and not a pointed oval. The second eye is not visible. The nose, which should be located in the middle and between the eyes, went somewhere completely to the edge of the contour, and you could not find a mouth at all - definitely, a dark corner from the bottom-left does not look like it at all. Do not face - you decide, and throw the picture in the trash.
So we would think if our visual system was engaged in a simple comparison of patterns in images. Fortunately, she thinks somehow differently. The absence of a second eye does not cause any concern to us; this makes the face no less resembling a face. We mentally pretend that the second eye should be on the other side, and its shape is due solely to the fact that the head in the photo is turned and looks to the side. It seems impossible to be trivial when you try to explain it in words, but some of you would seriously disagree with you.
The most annoying thing is that you cannot see how this question can be solved mechanically. Computer vision has been confronted with the relevant problems for a very long time, since its inception, and periodically found effective private solutions - so, we can identify a subject that has been moved to the side, consistently moving our test pattern across the entire image (which convolution networks use successfully), we can cope with scaled or rotated pictures using SIFT, SURF and ORB signs, but the effects of perspective and the rotation of an object in the scene space seem to be of a qualitatively different level. Here we need to know how the object looks from all sides , to get its true three-dimensional shape, otherwise we have nothing to work with. Therefore, to recognize the pictures, you do not need to recognize the pictures . They are false, deceptive and obviously inferior. They are not our friends.
3. Finally, to practice (actually not)
So, the important question is how do we get a three-dimensional model of everything we see? An even more important question is how to do without the need to buy a laser spatial scanner (at first I wrote “damn expensive laser scanner”, and then came across this post )? Even not so much for the reason that we are sorry, but because the animals in the process of evolution of the visual system obviously somehow did without it, only with their eyes, and it would be curious to find out how they are.
Somewhere in this place, a part of the audience usually gets up and leaves the hall, cursing for marking time - everyone knows that we use binocular vision to perceive depth and space, we have two special eyes for this! If you think so too, I have a little surprise for you - this is not true. The proof is beautiful in its simplicity - just close one eye and walk around the room to make sure that the world has not suddenly lost its depth and does not look like a flat analogue of an animated cartoon. Another way is to go back and look at the photo with the railroad again, where the depth can be clearly seen even though it is located on a completely flat monitor surface.
Generally with two eyes, everything is not so simple
For some actions, they seem to be true in terms of spatial positioning. Take two pencils, close one eye, and try to move these pencils so that they touch the tips of the leads somewhere near your face. Most likely, the leads will disperse, and noticeably (if you can easily, bring them closer to the face), while this does not happen with the second open eye. The example is taken from Mark Trangizi's book “The Revolution in Sight” - there is a whole chapter on stereopsis and binocular vision with a curious theory that we need two eyes looking forward in order to see through small clutters like hanging leaves. By the way, a funny fact - in the first place in the list of advantages of binocular vision on Wikipedia is "It gives a creature."
So, binocular vision does not suit us - and with it we reject stereo cameras, range finders and Kinect. Whatever the ability of our visual system to recreate three-dimensional images of the seen, it clearly does not require two eyes. What remains in the end?
I am by no means ready to give an exact answer in relation to biological vision, but perhaps, for the case of an abstract robot with a camera instead of an eye, there is one promising way. And this way is movement.
Back to the train theme, only this time we look out the window:

What we see at the same time is called “motion parallax”, and in short it lies in the fact that when we move sideways, close objects shift into the field of view more than distant ones. For moving forward / backward and turning, we can also formulate the relevant rules, but let's ignore them for now. So, we are going to move, assess the displacements of objects in the frame and on the basis of this, determine their distance from the observer - a technique that is officially called “structure-from-motion”. Let's try.
4. Finally, to practice
First of all - have they done everything, by chance, before us? The “Structure from motion” page on Wikipedia offers as many as thirteen tools (and these are only open source) for recreating 3D models from a video or a set of photos, most of them use an approach called bundle adjustment, and the most convenient one seemed to me Bundler (and demo he is cool). Unfortunately, there is a problem that we still face - the Bundler wants to know the camera model and its internal parameters from us (as a last resort, if the model is unknown, it requires you to specify the focal length).
If this is not a problem for your task, you can safely stop reading, because this is the simplest and at the same time effective method (do you know, by the way, what were the models used in the game “The Disappearance of Ethan Carter” ?). For me, alas, the need to be tied to a camera model is a condition that I would very much like to avoid. Firstly, because we have a full YouTube visual video experience that we would like to use in the future as a sample. Secondly (and this may be even more important), because our human brain, it seems, if it knows in numbers the internal parameters of the camera of our eyes, it is perfectly able to adapt to any optical distortion. Looking through the lens of a wide-focus camera, fishing, watching movies and wearing oculus does not completely destroy your visual abilities. So, probably, some other way is possible.
So, we sadly closed the page
1. Take two shots taken from a calibrated camera.
2. Together with the calibration parameters (camera matrix), put them both into the stereoRectify function, which rectifies these two frames - this is a transformation that distorts the image so that the point and its displacement are on the same horizontal line.
3. We put these rectified frames into the stereoBM function and get a disparity map — such a picture in shades of gray, where the pixel is brighter, the more displacement it expresses (there is an example by reference).
4. Put the resulting displacement map into a function with the speaker name reprojectImageTo3D (we will also need the Q matrix, which we will receive among others in step 2). We get our three-dimensional result.
Hell, it looks like we are stepping on the same rake - in paragraph 1 we are required to use a calibrated camera (although OpenCV graciously gives us the opportunity to do it ourselves). But hey, here's a plan. B. In the documentation, there is a function with the suspicious name stereoRectifyUncalibrated ...
Plan b:
1. We need to estimate the approximate part of the displacements by ourselves - at least for a limited set of points. StereoBM is not suitable here, so we need some other way. A logical option would be to use feature matching - find some special points in both frames and select mappings. About how this is done, you can read here .
2. When we have two sets of matching points, we can throw them into findFundamentalMat to get the fundamental matrix that we need for stereoRectifyUncalibrated.
3. Run stereoRectifyUncalibrated, we get two matrices for rectifying both frames.
4. And ... and then it is not clear. We have rectified frames, but there is no Q matrix, which was needed for the final step. Googling, I came across about the same perplexity of the post , and realized that I either missed something in theory, or did not think about this moment in OpenCV.
OpenCV: we are 2-0.
4.1 Change the plan
But wait. Perhaps, from the very beginning, we didn’t go the wrong way. In previous attempts, we, in fact, tried to determine the real position of three-dimensional points - hence the need to know the parameters of the camera, the matrix, rectify frames, and so on. In fact, this is the usual triangulation: on the first camera I see this point here, and on the second here - then we draw two rays passing through the centers of the cameras, and their intersection will show how far the point is from us.
This is all fine, but generally speaking, we do not need it. The real sizes of objects would interest us if our model would be used later for industrial purposes, in some 3d-printers. But we are going (this goal has already spread slightly, really) to push the data into the neural network and similar classifiers. For this we need only know the relative sizes of objects. They, as we still remember, are inversely proportional to the parallax displacements - the farther the object is from us, the less it shifts during our movement. Is it possible to somehow find these offsets even easier, simply by somehow matching both pictures?
Of course, you can. Hi, optical flow .
This is a great algorithm that does exactly what we need. Put in it a picture and a set of points. Then we put the second picture. We get at the output for given points their new position in the second picture (approximate, of course). No calibrations and no mention of the camera at all - the optical flow, despite the name, can be calculated on the basis of anything. Although usually it is still used for tracking objects, collision detection, and even augmented reality .
For our purposes, we (for the time being) want to use Gunnar Farnebak's “dense” flow, because he can calculate the flow not for any particular points, but for the whole picture at once. The method is available using calcOpticalFlowFarneback, and the very first results are beginning to be very, very good - see how much it looks cooler than the previous result stereoRectifyUncalibrated + stereoBM.

Many thanks to the great game Portal 2 for the opportunity to build your own rooms and play cubes. I'm doin 'Science!
The code for this little demo
# encoding: utf-8 import cv2 import numpy as np from matplotlib import pyplot as plt img1 = cv2.imread('0.jpg', 0) img2 = cv2.imread('1.jpg', 0) def stereo_depth_map(img1, img2): # 1: feature matching orb = cv2.ORB() kp1, des1 = orb.detectAndCompute(img1, None) kp2, des2 = orb.detectAndCompute(img2, None) bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True) matches = bf.match(des1, des2) matches = sorted(matches, key=lambda x: x.distance) src_points = np.vstack([np.array(kp1[m.queryIdx].pt) for m in matches]) dst_points = np.vstack([np.array(kp2[m.trainIdx].pt) for m in matches]) # 2: findFundamentalMat F, mask = cv2.findFundamentalMat(src_points, dst_points) # 3: stereoRectifyUncalibrated _, H1, H2 = cv2.stereoRectifyUncalibrated(src_points.reshape(src_points.shape[ 0], 1, 2), dst_points.reshape(dst_points.shape[0], 1, 2), F, img1.shape) rect1 = cv2.warpPerspective(img1, H1, (852, 480)) rect2 = cv2.warpPerspective(img2, H2, (852, 480)) # 3.5: stereoBM stereo = cv2.StereoBM(cv2.STEREO_BM_BASIC_PRESET, ndisparities=16, SADWindowSize=15) return stereo.compute(rect1, rect2) def optical_flow_depth_map(img1, img2): flow = cv2.calcOpticalFlowFarneback(img1, img2, 0.5, 3, 20, 10, 5, 1.2, 0) mag, ang = cv2.cartToPolar(flow[..., 0], flow[..., 1]) return mag def plot(title, img, i): plt.subplot(2, 2, i) plt.title(title) plt.imshow(img, 'gray') plt.gca().get_xaxis().set_visible(False) plt.gca().get_yaxis().set_visible(False) plot(u' ', img1, 1) plot(u' ( )', img2, 2) plot(u'stereoRectifyUncalibrated', stereo_depth_map(img1, img2), 3) plot(u' ', optical_flow_depth_map(img1, img2), 4) plt.show() So, great. We have displacements, and they look quite good. How now do we get from them the coordinates of three-dimensional points?
4.2 Part in which we get the coordinates of three-dimensional points
This picture is already flashed on one of the links above.

The distance to the object is calculated here using the school geometry method (similar triangles), and it looks like this:
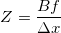 . And the coordinates, respectively, like this:
. And the coordinates, respectively, like this: 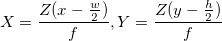 . Here, w and h are the width and height of the image, they are known to us, f is the focal length of the camera (the distance from the center of the camera to the surface of its screen), and B is the same pitch. By the way, please note that we slightly violate the generally accepted names of the axes here, when Z is directed upwards - we have Z looking at the depth of the screen, and X and Y - respectively, are directed along the width and height of the picture.
. Here, w and h are the width and height of the image, they are known to us, f is the focal length of the camera (the distance from the center of the camera to the surface of its screen), and B is the same pitch. By the way, please note that we slightly violate the generally accepted names of the axes here, when Z is directed upwards - we have Z looking at the depth of the screen, and X and Y - respectively, are directed along the width and height of the picture.Well, everything is simple about f - we have already stipulated that the real parameters of the camera do not interest us, if only the proportions of all the objects would change according to one law. If we substitute Z into the formula for X above, then we can see that X doesn’t depend on focal length at all (f is reduced), so its different values will change only the depth - “stretch” or “flatten” our scene. Visually, it is not very pleasant, but again, for the classification algorithm, it doesn’t matter anyway. So let's set the focal length in an intelligent way - just think of it. I, however, reserve the right to slightly change the opinion further in the text.
About B is a bit more complicated - if we don’t have a built-in pedometer, we don’t know what distance the camera has moved in the real world. So let's think a little while and decide that the camera movement is approximately smooth, we have a lot of frames (a couple of tens per second), and the distance between two neighboring ones is about the same, i.e.
 . And again, then we will slightly clarify this situation, but for now let it be so.
. And again, then we will slightly clarify this situation, but for now let it be so.It's time to write some code.
import cv2 import numpy as np f = 300 # , - , B = 1 w = 852 h = 480 img1 = cv2.imread('0.jpg', 0) img2 = cv2.imread('1.jpg', 0) flow = cv2.calcOpticalFlowFarneback(img1, img2, 0.5, 3, 20, 10, 5, 1.2, 0) mag, ang = cv2.cartToPolar(flow[..., 0], flow[..., 1]) edges = cv2.Canny(img1, 100, 200) result = [] for y in xrange(img1.shape[0]): for x in xrange(img1.shape[1]): if edges[y, x] == 0: continue delta = mag[y, x] if delta == 0: continue Z = (B * f) / delta X = (Z * (x - w / 2.)) / f Y = (Z * (y - h / 2.)) / f point = np.array([X, Y, Z]) result.append(point) result = np.vstack(result) def dump2ply(points): # .ply, with open('points.ply', 'w') as f: f.write('ply\n') f.write('format ascii 1.0\n') f.write('element vertex {}\n'.format(len(points))) f.write('property float x\n') f.write('property float y\n') f.write('property float z\n') f.write('end_header\n') for point in points: f.write('{:.2f} {:.2f} {:.2f}\n'.format(point[0], point[2], point[1])) dump2ply(result) Here is the result. I hope this gif has time to load while you read this far.
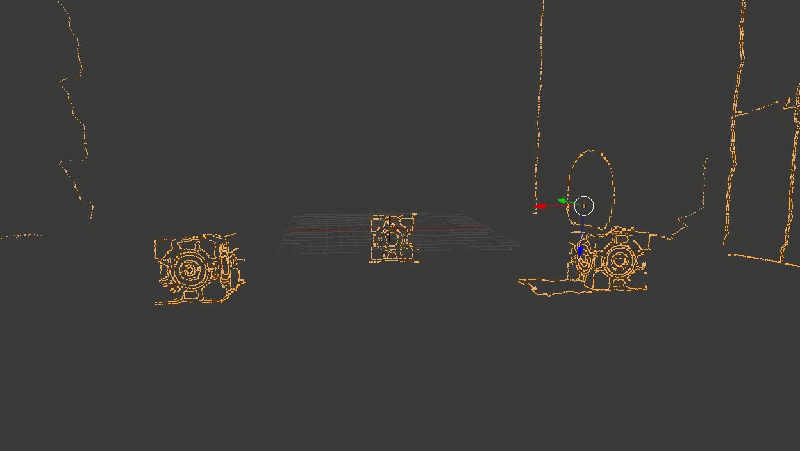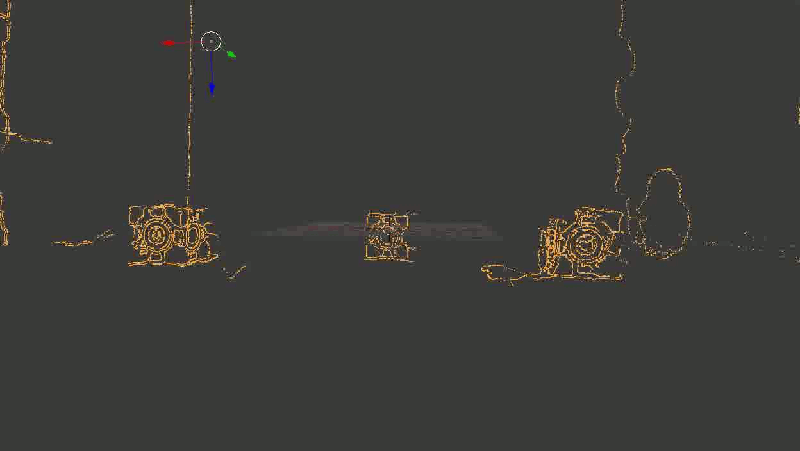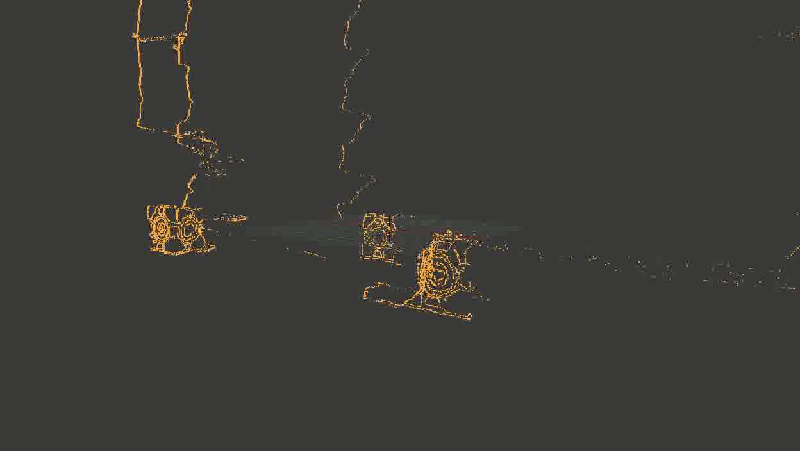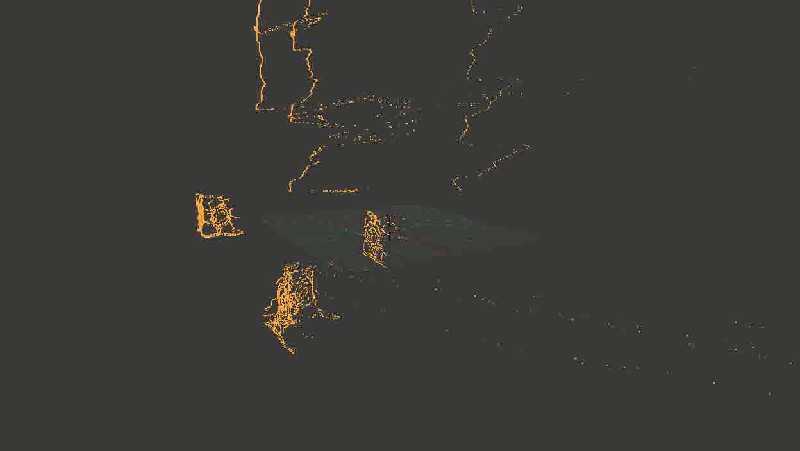
For clarity, I took not all points in a row, but only the borders highlighted by the Canny-detector
At first glance (in any case, to me) everything seemed to be excellent - even the angles between the faces of the cubes formed pretty ninety degrees. The objects in the background got worse (notice how the contours of the walls and the door were distorted), but hey, it's probably just a little noise, it can be cured using more frames or anything else.
Of all the possible hasty conclusions that could be made here, this turned out to be the furthest from the truth.
5. The part in which nothing happens
In general, the main problem was that some of the points were rather distorted. And - an alarming sign, where it was time to suspect that something was wrong - was distorted not in a random way, but approximately in the same places, so it was impossible to correct the problem by successively superimposing new points (from other frames).
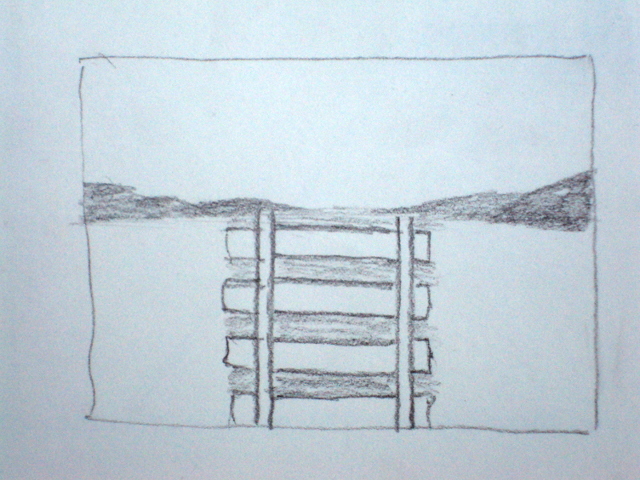
It looked like this: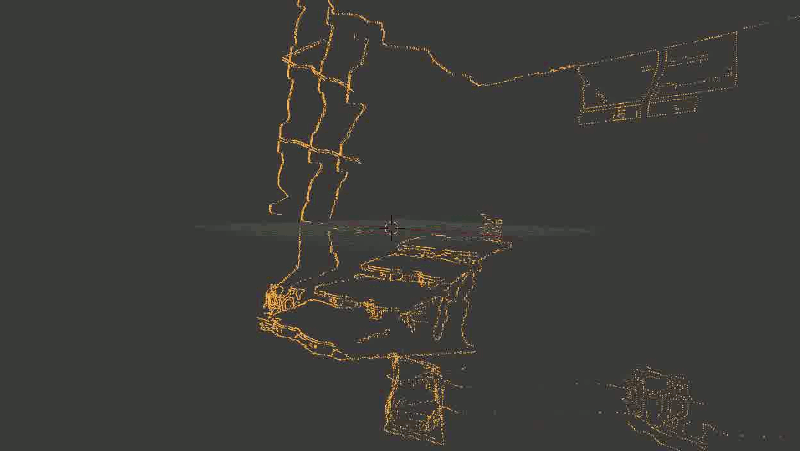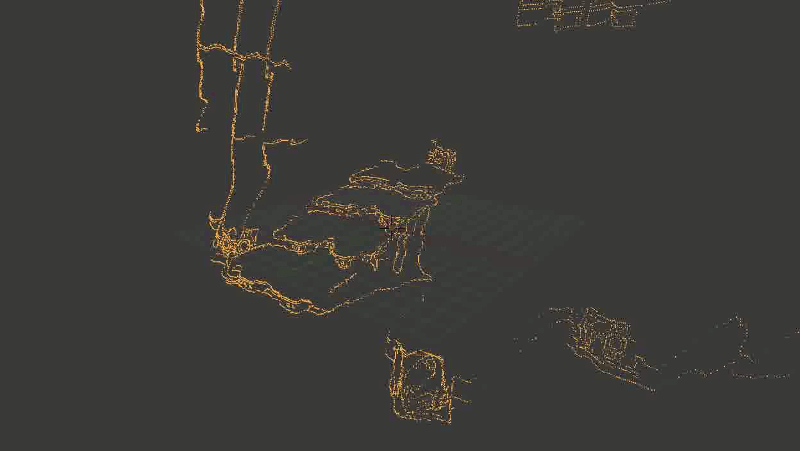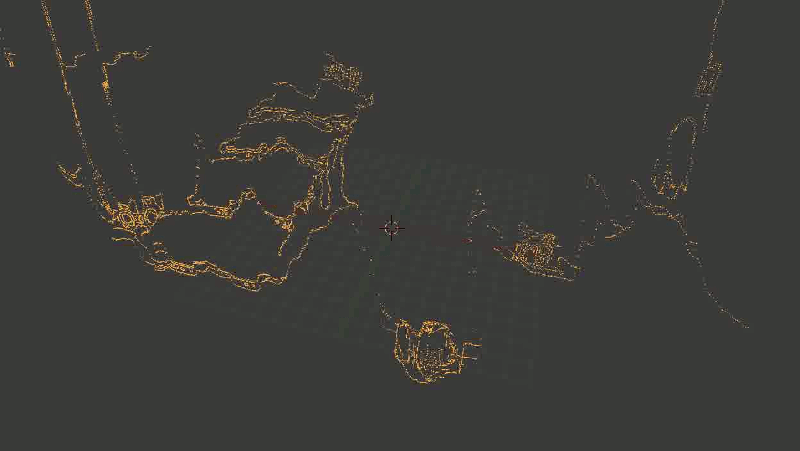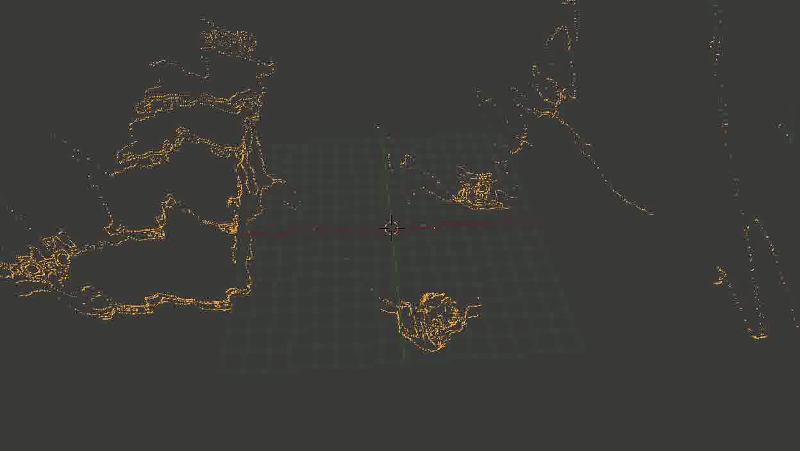
The staircase is crushed, sometimes turning into an amorphous piece of incomprehensible-what.
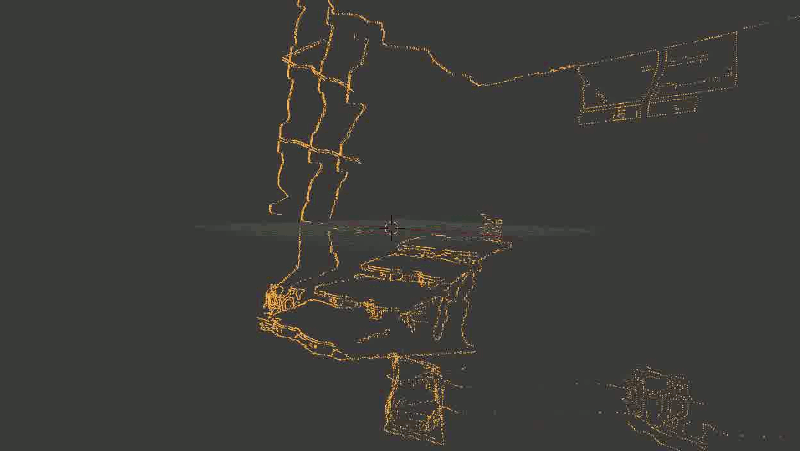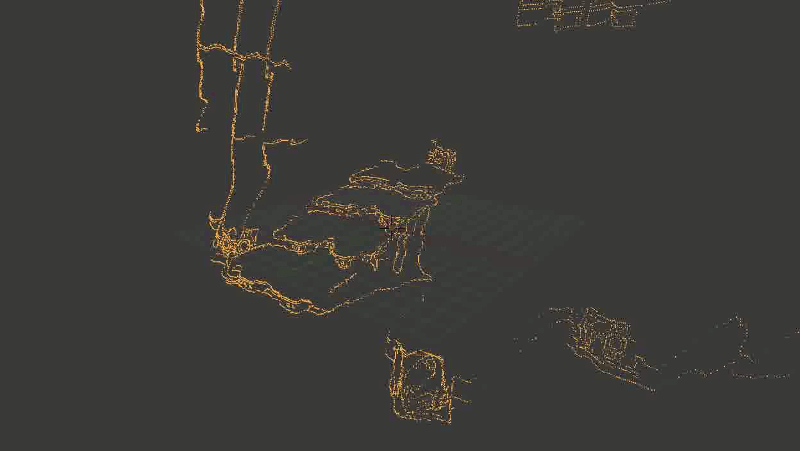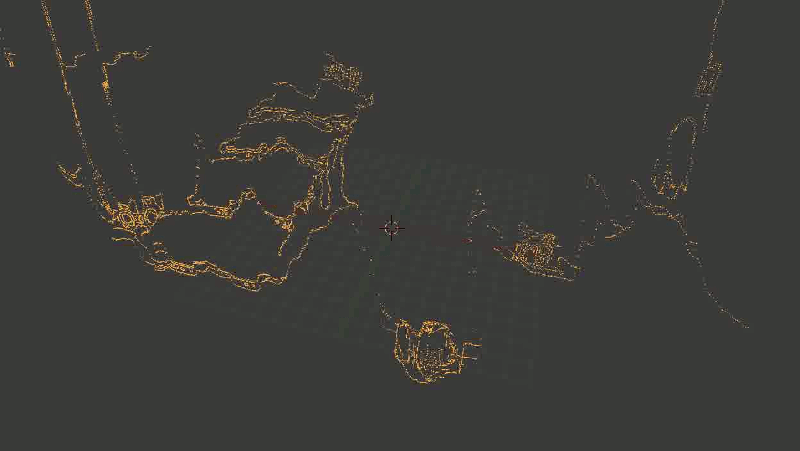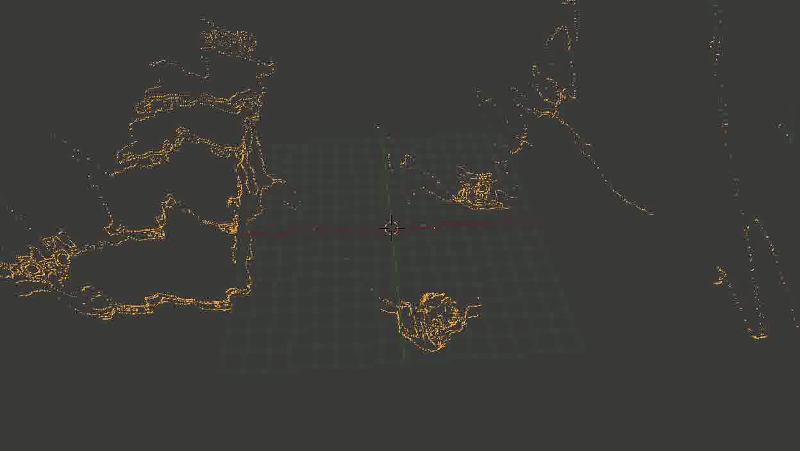
The staircase is crushed, sometimes turning into an amorphous piece of incomprehensible-what.
I tried to fix it for a very long time, and during that time I tried the following:
- smooth karinka with optical flow: blur according to Gauss, median filter and a fancy bilateral filter that leaves clear edges. It is useless: objects on the contrary, blurred even more.
- tried to find straight lines in the picture with the help of Hough transform and move them in the same direct state. Partly worked, but only on the borders - the surface still remained the same distorted; plus it was impossible to put a thought in the spirit of “what if there are no straight lines in the picture at all”.
- I even tried to make my own version of the optical stream, using OpenCV templateMatching. It worked like this: for any point we build a small (about 10x10) square around it, and we start moving it around and looking for the maximum match (if the direction of movement is known, then we can limit it around). It turned out quite well in places (although it worked clearly slower than the original version):

On the left is the familiar Farnebak stream, on the right is the above described bike.
In terms of noise, alas, it turned out no better.
In general, everything was bad, but very logical. Because it should be so.

Illustration to the problem. Moving here is still a step to the right.
Let's pick some green dot from the image above. Suppose we know the direction of motion, and are going to look for the “displaced twin” of our green point, moving in a given direction. When do we decide that we have found the desired twin? When we stumble upon some kind of “landmark”, a characteristic site that is similar to the environment of our starting point. For example, on the corner. The angles in this respect are easy to track, because they themselves are quite rare. Therefore, if our green point is an angle, and we find a similar angle in a given neighborhood, then the problem is solved.
The situation with the vertical line (the second left green dot) is slightly more complicated, but still easy. Considering that we are moving to the right, we will meet the vertical line only once for the entire search period. Imagine that we are crawling with our search window in the picture and see a monophonic background, background, again a background, a vertical segment, again a background, a background, and again a background. Also easy.
The problem occurs when we try to track a piece of the line parallel to the movement . The red dot does not have one clearly pronounced candidate for the role of a displaced twin. There are many of them, they are all close by, and it’s simply impossible to choose any one method we use. This is a functional limitation of the optical flow. As Wikipedia kindly warns us in the relevant article, "We cannot solve this problem, and there is nothing to be done.
Absolutely nothing?
Generally, to be honest, this is probably not entirely true. After all, you can find on the right picture a match for the red dot? This is also not very difficult, but for this we mentally use some other method - we find the nearest “green point” (the bottom corner) nearby, estimate the distance to it and put the corresponding distance on the second face of the cube. Optical flow algorithms have room to grow - this method could be adopted (if this has not yet been done).
6. Green Dots FTW
In fact, as late common sense prompts at this point, we are still trying to do extra work that is not important for our ultimate goal — recognition, classification, and other intelligence. Why are we trying to cram all the points in the 3D world? Even when we work with two-dimensional images, we usually do not try to use each pixel for classification - most of them do not carry any useful information. Why not do the same here?
Actually, everything turned out just like that. We will calculate the same optical flow, but only for green, stable points. And by the way, in OpenCV we have already been taken care of. The thing we need is called the Lucas-Canada stream.
It will be a bit boring to give the code and examples for the same cases, because you get the same thing, but with a much smaller number of points. On the way, let's do something else: for example, let's add the ability to process camera turns to our algorithm. Before that, we were moving exclusively sideways, which is quite rare in the real world outside of train windows.
With the advent of turns, the coordinates of X and Z are mixed together. Let's leave the old formulas for calculating coordinates relative to the camera, and we will translate them into absolute coordinates as follows (here
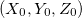 - coordinates of the camera position, alpha - angle of rotation):
- coordinates of the camera position, alpha - angle of rotation):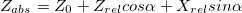
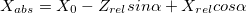

(cheater; it's because we think the camera doesn't move up and down)
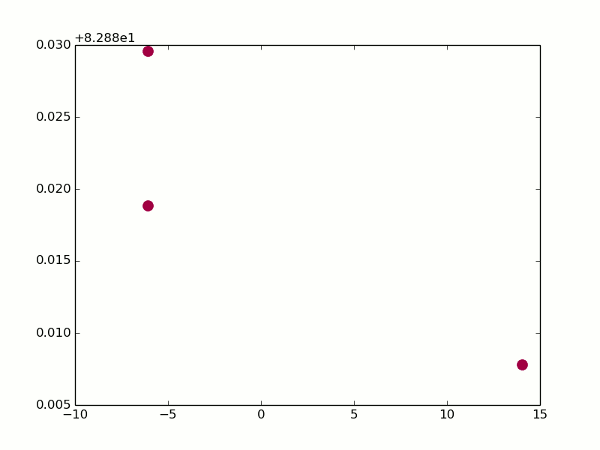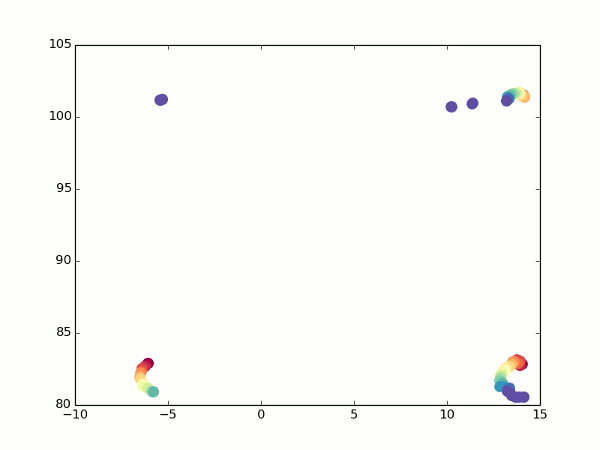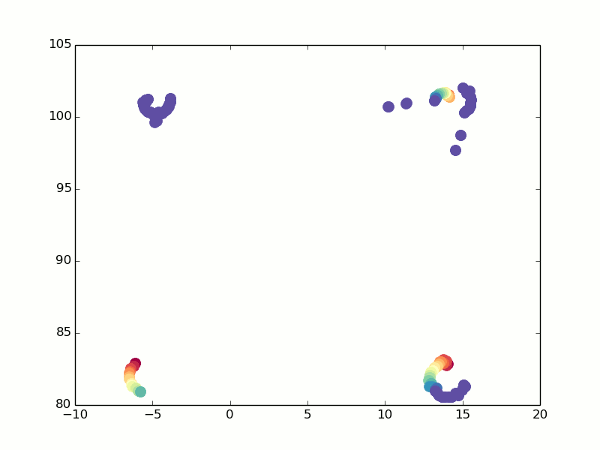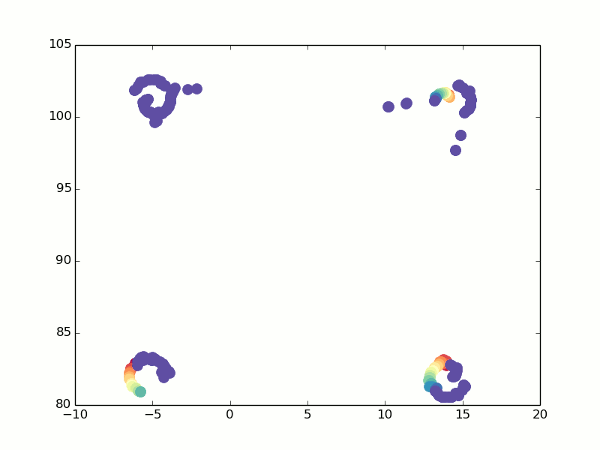
Somewhere here we have problems with focal length - remember, we decided to set it arbitrary? So, now, when we had the opportunity to estimate the same point from different angles, it began to matter - precisely because the coordinates X and Z began to interfere with each other. In fact, if we run a code similar to the previous one, with an arbitrary focus, we will see something like this:

It is not obvious, but it is an attempt to arrange a camera bypass around a regular cube. Each frame - evaluation of visible points after the next rotation of the camera. Top view, as on the minimap.
Fortunately, we still have an optical stream. When turning, we can see which points pass into which, and calculate the coordinates for them from two angles. From here, it’s easy to get the focal length (just take the two formulas above for different alpha values, equate the coordinates and express f). So much better:

Not that all points would lie ideally one into another, but you can at least guess that this is a cube.
And finally, we need to somehow deal with the noise due to which our estimates of the position of points do not always coincide (see on the top of the hypha neat uneven ringlets? Instead of each of them, ideally, there should be one point). There is already room for creativity, but the most adequate way seemed to me like this:
- when we have several shifts to the side in a row, we combine information from them together - so for one point we will have several depth estimates at once;
- when the camera rotates, we try to combine two sets of points (before turning and after) and adjust one to the other. This fitting is correctly called “registration of points” (which you would never have guessed when hearing the term in isolation from the context), and for it I used the Iterative closest point algorithm to download the version for python + OpenCV;
- then the points that lie within the threshold radius (determined by the method of the nearest neighbor) merge together. For each point, we still track something like “intensity” - a counter of how often it was combined with other points. The greater the intensity - the greater the chance that this is an honest and correct point.
The result may not be as solid as in the case of cubes from the Portal, but at least, it is exact. Here are a couple of recreated models that I first uploaded to Blender, twirled the camera around them and saved the resulting footage:
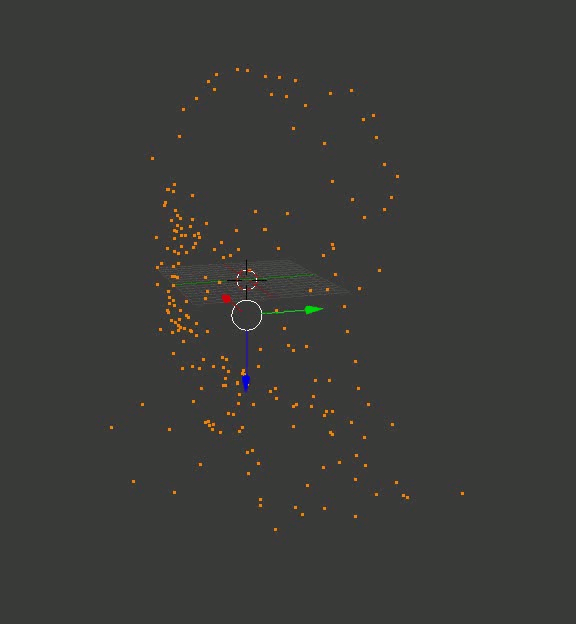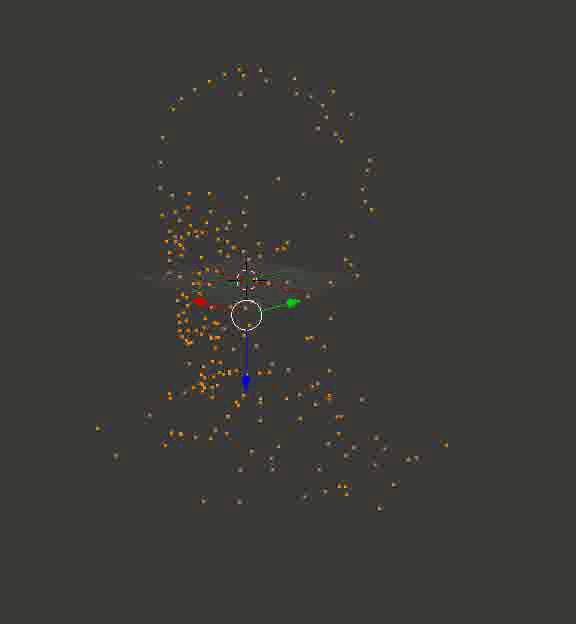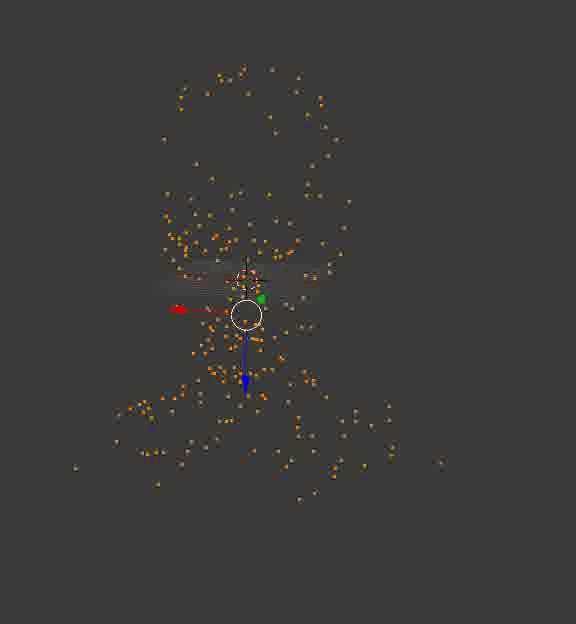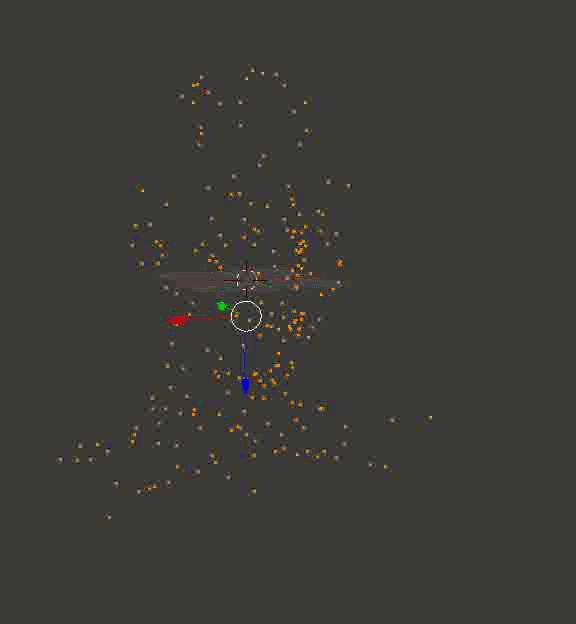
Professor Dowell's Head

Some random machine
Bingo! Then you need to push them all into the recognition algorithm and see what happens. But it, perhaps, we will leave on the following series.
application
Let's look back a little and remember why we all did it. The line of reasoning was:
- we need to be able to recognize the things depicted in the pictures
- but these pictures change every time when we change position or look at the same thing from different angles. Sometimes unrecognizable
- this is not a bug, but a feature: due to the fact that our limited eye sensors see only a part of the object, and not the entire object
- therefore, it is necessary to somehow combine these partial data from the sensors and collect from them the idea of the subject in its full form.
Generally speaking, this is certainly not just a problem of sight. This is rather a rule, not an exception - our sensors are not omnipotent, they constantly perceive information about an object in parts - but it is curious how all such cases can be combined into some common framework? Say (returning to vision), your eyes are now constantly making small and very fast movements - saccades - jumping between objects in sight (and in the intervals between these movements your vision does not work at all - that is why you cannot see your own saccades, even when you stare at the mirror point blank). The brain is constantly engaged in hard work on the "stitching" of the pieces. Is this the same task that we just tried to solve, or is it another? Perception of speech, when we can relate a dozen different variants of the pronunciation of a word with one of its “ideal” spelling - is this a similar task too? What about the reduction of synonyms to one "image" of the subject?
If so, then perhaps the problem is somewhat more than just a parietal algorithm of the visual system, which replaces the laser pointer of the scanner with our under-evolved eyes.
Obvious considerations say that when we try to recreate some thing seen in nature, there is no point in blindly copying all its constituent parts. To fly through the air, waving wings and feathers are not needed, a stiff wing and lift are sufficient; To run fast, you do not need mechanical legs - the wheel will cope much better. Instead of copying what we saw, we want to find a principle and repeat it on our own (maybe, making it easier / more efficient). What is the principle of intelligence, an analogue of the laws of aerodynamics for flight, we do not yet know. Deep learning and Yan Lekun, his prophet (and many other people following him) believe that one should look towards the ability to build "deep" hierarchies of features from the data obtained. Maybe we can add to this one more clarification - the ability to combine together relevant pieces of data, perceiving them as parts of one object and placing them in a new dimension?
Source: https://habr.com/ru/post/249661/
All Articles