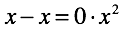Divide by zero is the norm. Part 2
Part 1. Actually, everyone has already divided everything up to us!
Part 2. Truth is somewhere nearby
In the last part, we extended algebra and were able to divide by zero arithmetically. As a bonus, the method was not the only one. However, all these algebras did not give an answer to the question: “What’s inside or why we don’t show it?”
While the ancient knitted knots , this question could not arise . Now, wherever you look, “blah blah, for a ≠ 0”. So the answer lies somewhere between the knots and the present. In mathematics, everything is strictly and consistently, and therefore the answer could not be lost.
')
We will try to get as close to the answer as possible. This part is almost entirely devoted to the philosophy of arithmetic. Most likely a part of the material will be trivial for you. However, we do not have a repetition of the school course of arithmetic here.
The material is designed to highlight the structure of arithmetic. We will bite into it from different sides and tear off the layers. The goal is to understand what lies there.
To rush back into the wilds, I would like to understand why this question periodically arises and why it is worth looking for an answer.
Let us remember the school years, the time when we were first told: “It is impossible to divide by zero, this is so categorical. - You can not and everything! But before that in mathematics everything was logical and consistent. They folded the watermelons and read the melons, the apples rolled. From nowhere, at the very start of the study of mathematics, the first forbidden fruit appeared.
But the education system does not spare anyone ( proof ). There is no other way but to go further and learn new knowledge. A “leap of knowledge” occurs in the head, as if the millennium of the evolution of mathematics had been missed. And this is just the beginning.
Formulas of a circle and triangles, a discriminant, trigonometric identities, etc., appear in high school from nowhere. What unites them? They all came from above, completely unknown from where. They just need to be used, in the worst case to notch.
Once in high school, the majority, instead of returning to the missed material, studies the “tower” with a bias in the specialty. The volume of formulas that came from above does not bother you at all.
Yes, the education system can be understood. The specialist is paid for the result, and not for what he knows from where the exhibitor in his calculations.
As a result, we do not come to conclusions, as mathematicians do. At the moment of the “leap of knowledge,” that is, when we discard a part of logical chains, the sacrament is decided. We take on faith what they tell us. The textbook turns into a scripture!
The prohibition of division by zero is the first and most intrusive ban on mathematics. Therefore, it is remembered for a lifetime. This is also a pedagogical problem that leaves an imprint on the whole of mathematics, as if on a “mystery covered in darkness”. This is a difficult problem, compared to it, to find the majority of the missing logical chains is not difficult.
You can turn a scripture back into a textbook. The reason for the ban should be strictly defined. The task of teachers to present it clearly. Science should not sow doubt.
Captain Obvious asserts that to divide by zero you need to know what division is and what zero is. Sadly, Google suggests that many adherents of the "division by zero magic" do not even go through the first round of this hell. Namely, to understand what they are going to do and with what. Take a look at Wikipedia:
It seems that the most useful thing we have found here is the connection between operations. It can be said that division is the third spinning wine, multiplication and subtraction - the second, and addition - the first. Perhaps for this reason, the division began to fail when working with zero.
So, only the addition operation contains a rule about how to determine the result of the operation (the sum) using two initial arguments (terms). All other arithmetic operations use this rule (matching numbers), but in addition impose their “additional conditions” .
Depending on the “additional conditions” arithmetic operations can be divided into direct and inverse :
All direct operations have the same property. They are closed . That is, the type of result is completely determined by the types of input numbers (it is impossible to obtain a fractional result from the product of two integers).
Inverse operations are only partially closed (the value of the root of an integer can be an integer, or it may not). In those cases where the result fails, the operation is undefined . This problem has long been solved in a simple way: consider the resulting operation record and numbers as a new type of numbers:
.
Thus, we can say that the inverse operations and “generate” new types of numbers.
Mathematical language:
Let us try to structure our understanding of arithmetic operations and the types of numbers they generate. For clarity, let us present one of the options, how the evolution of arithmetic can go.
We are in a cave. With the ability to count, no one was born. However, in the process of “contemplation”, an understanding emerged that such a concept is “quantity” . That is, we know that two mammoths and two apples have something in common and we can express this by bending our fingers. Accordingly, nothing but natural numbers at this stage we do not know.
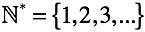
The set of natural numbers is marked with an asterisk “*” for uniqueness . Hereinafter, the absence of the concept of “zero” is emphasized.
There are several formal definitions of the sequence of natural numbers. We will take Peano's axiom as a basis. It is remarkable that these definitions were not described by the ancients. They appeared only in the 19th century, and after they passed the refinement procedure (in the original version there were nine, in the modern form already five).
Consider the formal definitions and their essence within our task (the traditional verbal description can be found on Wikipedia ):
What conclusion can be drawn from these axioms? A ban on looping in any form (global or local) is introduced. A ban on looping always requires the following element. This is how the mathematical concept of "infinity" based on the concept of "quantity" appears. The concept of “infinity” cannot exist without the concept of “quantity”.
Mathematical language:
The first operation that occurred during our evolution. As whole fingers do not bend, the result will be whole. Is that the leader of the sum of the fingers may be a little more than all the rest. If your fingers are not enough, you can always call a scientific assistant in the cave and expand the bit grid.
On Thursday, hunters shot 12 mammoths. For Friday we ate 5 of them. How many mammoths are left?
The task is well solved by introducing the extension of the fingers. But the approach does not always work. For example, to estimate stocks for the weekend, the hunter bends seven fingers for the rest, straightens five fingers for Saturday (the rate of consumption per day) and “tries” to open it for Sunday.
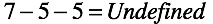
At this point, an “arithmeticException” occurs between “try” and “catch”. The result is not defined . Our operation is defined only for the case when the deductible is greater than the deductible.
However, the definition of subtraction does not impose any restrictions. To get rid of the requirement “a> b”, we introduce a “permutation rule” . That is, let us interchange the position of what is decremented and subtracted. But in order for the identity to remain true, the result needs to be marked with some sort of marker, for example, a minus sign. Any markers for mathematics are common (for example, the sign of the absence of zero in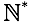
).
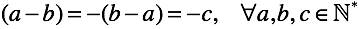
Due to the auxiliary operation “permutations” we came to the first abstraction - “ negative numbers ”. Marking in the form of a minus sign in a natural number is nothing more than a sign of deferred subtraction (but this is only for now).
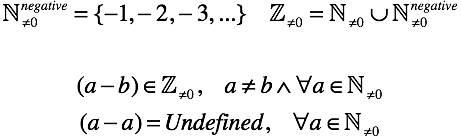
We have only one non-definite case, when the diminished and subtracted are equal. If we want to define it, then we will have to answer the question what is the concept of “nothing” . Although what all these difficulties are for, let us denote “nothing” by the symbol “0” (later we shall fully understand).
It remains to fix our decision in the form of “rules for addition / subtraction of zero” . They follow from the definition of zero after a couple of simple permutations:
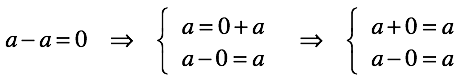
Let's see how well the rules entered. Solving equations, we can always find the unknown third from two known numbers. It does not matter in what part of the equation it is, the solution is always unique.
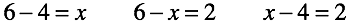
Negative numbers appeared as a result of the permutation, zero filled out “nothing”. Negative numbers and zero are born in different ways. Next, we will consider two branches of evolution: separately all numbers without zero and separately zero.
Multiplication is by definition a shortened record of addition. Multiplying the natural numbers, the result can only be natural. At this stage of evolution, the usefulness of the definition for us ends.
For negative numbers in the definition there is not a word about how to multiply them. These rules were formed gradually in the course of solving applied problems . In the modern interpretation, they are known as an addition to the multiplication in the form of “rules of signs” . They are defined so well that by applying them to non-zero integer numbers, the operation remains closed.
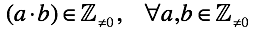
In the case of zero, the situation is radically different. One more rule is introduced: “the rule of multiplication of zero“ (multiplication of any number by zero gives zero). But this rule only seems new. We cannot introduce any other rule. The definition of multiplication strictly connects us with addition. Expanding multiplication through addition, we use the “rules of addition / subtraction of zero,” respectively, we can get nothing but zero.
Mathematical language:
Division is the inverse operation of multiplication. In equations with positive and negative numbers, it becomes possible to substitute non-multiple numbers.
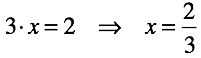
As a consequence, the operation generates rational numbers .
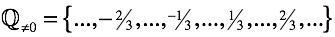
To inscribe them in arithmetic, the set includes “rules for actions with ordinary fractions” . Fortunately, these rules harmoniously coexist with the “rules of signs” that we introduced earlier. As a result, it is still possible in equations to determine the unknown with any arrangement using two known numbers.
In the case of zero, it can be multiplied by rational numbers. That's all, the harmony is over! For only two of the three types of equations with arbitrary numbers, a solution can be found.
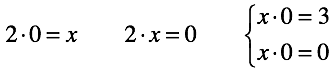
First, it became possible to make an equation with numbers that are not so convenient that we cannot find a single solution. The solution is “not possible.”
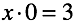
Secondly, the opportunity to make an equation in which there is an infinite number of solutions. It is also impossible to choose one of them. The solution is “not unique”.
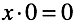
It is easy to guess, the root of the problem of division by zero lies in the “impossibility” and “ambiguity” of multiplying zero. Multiplication, in turn, retransmits the “addition / subtraction zero rules”. In fact, you can set equations that have the same properties, using only addition.
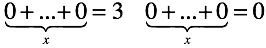
In both equations, you need to determine the number of zeros that you need to add to get an arbitrary number or zero.
The division did not bring something qualitatively new. There was a transformation of the "impossibility" and "ambiguity" of addition to concrete entities , in the form of uncertainty 1/0 and 0/0, respectively.
It turns out that the division, as the first suspect, is not to blame for the fact that it is impossible to divide by zero.
As long as the concept of “zero” does not exist, all operations, including exponentiation and taking the root (logarithm), are well closed (already true on complex numbers) and arithmetic works great. But there is one “but”, with this configuration of arithmetic, the subtraction operation turns out to be not fully determined.
After introducing zero, addition and subtraction work well. For other operations, it is more likely to install crutches (
) than an equal number.
So, since the division operation was not to blame for the prohibition of division by zero. Then let's try to put together everything that we know about zero:
On the last point it is worth staying in more detail. Let's try to present not an absolute zero.
Suppose we have a mammoth. For its transportation need packaging. If you put a mammoth in a container, and then pull it out, then the container will be “nothing” (just like in the picture with the match above). However, the packaging for two mammoths is somewhat different from the packaging for one. In the case of theft, there is reason to charge in accordance with the size of the remaining container. So, there are situations when one “nothing” to another “nothing” is different.
Can “nothing” be different or “nothing” is a single and absolute essence? This is a question that cannot be answered . The debate on whether there is a God is analogous and meaningless, but is it one or many of them. The answer in this world, we will not know.
Mathematical language:
Well, the answer to the question of how many zeros should be arithmetic cannot give. We use one zero. In the wheels considered in the first part, arithmetic with an infinite number of zeros was used. And can there be a finite number of zeros, but more than one.
Maybe such arithmetic successfully used. One of the clearest examples of arithmetic with “signed zero” , implemented in JavaScript.
Mathematical language:
It can be concluded that uncertainties in arithmetic will persist as long as the number of zeros is finite.
By and large, it does not matter how we treat zero. Do we need a single and absolute zero, and maybe a couple or an infinite number, arithmetic can always adjust to us.
Finally, I would like to present at least one version of a numerical axis containing an infinite number of zeros (this example describes the concept and does not pretend to mathematical rigor).
For subtraction, when reducing and subtracting are equal, instead of entering zero we define the operation of “reduction”. That is, we allow deleting equivalent expressions with the opposite sign. But if we have reduced everything, then the result is no longer suitable for further use.
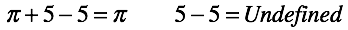
We start counting in the number axis from one (from the first number of the concept “quantity”). To generate the remaining numbers, we use the infinite sequence defined by the following function (it is also used in Peano's axioms ). This will be our reference generator of infinite sequence.
To get a very small number using the follow function, you need to expend as much force as on the generation of a very large one. We use the functions f (x) = 1 / x and f (x) = x. The task is not worth giving the decimal form a rational fraction, respectively, the computational complexity of the functions is the same.
Since neither “absolute zero” (marked with a zero symbol), nor “potential infinity” (marked with an unsigned infinity symbol) are unattainable, the axis grows from one infinitely in both directions (non-uniform scale).
When defining subtraction, a “permutation rule” is defined. We, in turn, make a copy of our direct and display it mirror. Twin numbers and unreachable limits are marked with a minus sign. Positive line, not connected with negative. The transition from one straight line to another is performed only by the “permutation rule”.
For clarity, we depict the resulting numerical line in the form of a circle. Just as we did with the projective extension. However, the limit values are not closed (we do not compactify). This transformation of the semantic load does not carry and is performed only to improve perception.
Now we are ready for the most important thing. Let us make the transition from a single potential infinity to an infinite set of actual infinities (a similar approach is used in non-standard analysis ).
We will treat infinitely large quantities as full numbers. For the reference actual infinity, we take the “speed” at which the following function reaches any arbitrary number. We denote this number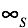
. Not to be confused with potential infinity. 
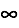She is still unattainable.
To obtain various actual infinities, we will use the notion of the limit of a function when tending to the number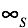 . We will not reject infinitesimally (of lower order) and will not absorb constants with infinitely large quantities, as is customary in classical analysis. We will save all the information component number. Accordingly, we have the opportunity to compare infinitely large numbers.
Raising the number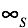 to negative degrees, we get infinitely small numbers. In fact, this is our infinite set of zeros, which can be compared with each other and used in arithmetic (as opposed to an infinitely small value in classical analysis).
Mathematical language:
If there is a practical need, we can define a subtraction operation and for equal numbers (instead of the “reduction” defined by us above). For example, it may be a lower order number than the original numbers.
(analogue of the equation of the wheel ). Arithmetic will be closed. But you need to be aware that the sum of two twos will immediately be equal to four with a tail. This is somewhat similar to the addition of speeds in the theory of relativity . Another example is thermodynamics and the concept of absolute zero temperature . Having stopped molecules, atoms continue to move. Having stopped atoms, quarks are still moving, etc. Immersion is infinite.
We are between the past and the future, between the micro and macro world. In all areas, sooner or later we find a limit beyond which we can not go and this is normal.
In math it's not like that. We are told that zero is a number. Then put it on par with all the other numbers. Then we are told that the length of the path from minus one to one is two. And at this moment our consciousness finally dissolves zero among the other numbers.
We cannot divide by zero, because we have forgotten that once the notion of “nothing” and the notion of “quantity” were mixed.
Part 2. Truth is somewhere nearby
In the last part, we extended algebra and were able to divide by zero arithmetically. As a bonus, the method was not the only one. However, all these algebras did not give an answer to the question: “What’s inside or why we don’t show it?”
While the ancient knitted knots , this question could not arise . Now, wherever you look, “blah blah, for a ≠ 0”. So the answer lies somewhere between the knots and the present. In mathematics, everything is strictly and consistently, and therefore the answer could not be lost.
')
We will try to get as close to the answer as possible. This part is almost entirely devoted to the philosophy of arithmetic. Most likely a part of the material will be trivial for you. However, we do not have a repetition of the school course of arithmetic here.
The material is designed to highlight the structure of arithmetic. We will bite into it from different sides and tear off the layers. The goal is to understand what lies there.
2. Truth is somewhere nearby
2.1 Why bother?
To rush back into the wilds, I would like to understand why this question periodically arises and why it is worth looking for an answer.
Let us remember the school years, the time when we were first told: “It is impossible to divide by zero, this is so categorical. - You can not and everything! But before that in mathematics everything was logical and consistent. They folded the watermelons and read the melons, the apples rolled. From nowhere, at the very start of the study of mathematics, the first forbidden fruit appeared.
The classic answer set only upsets
- “All is not possible!” Or “Check on the calculator” - without comments. Special pedagogical methodology.
- “Apple can be divided into two. You and friend Kohl. It is possible for three. And if a person is divided into zero, how many times should it be cut? ”- yes, it is not clear. Yes, and a question to answer the question indecent. And the teacher for what? They say that the mathematics is “beautiful”, the mathematics is “the queen”, and there is such an embarrassment.
- “2 ∙ 0 = 0 and 3 ∙ 0 = 0, we divide both equalities by zero, then it turns out that 2 = 0/0 and 3 = 0/0. So 2 = 3 or something? ”- an example, of course, illustrative. But such examples not only do not give an answer to the question, they also sow the fear of science. But what if it is impossible to divide or multiply. And what if I slip. Or maybe the teacher himself did not understand?
- “To understand you need a lot of knowledge. This is studied at an institution of higher education, and not all of them ”- well, yes, but why can't it be divided? Up to this point, our causal relationships have not been violated, they went from simple to complex. But zero is a number as a number. Division is an operation as an operation. Ban on level ground!
But the education system does not spare anyone ( proof ). There is no other way but to go further and learn new knowledge. A “leap of knowledge” occurs in the head, as if the millennium of the evolution of mathematics had been missed. And this is just the beginning.
" ... there is no need to show unnecessary haste, you need to give time to the student to get used to the inner revolution that takes place in it as a result of the act of knowledge " - F. Klein, "Elementary mathematics from the point of view of the highest"
Formulas of a circle and triangles, a discriminant, trigonometric identities, etc., appear in high school from nowhere. What unites them? They all came from above, completely unknown from where. They just need to be used, in the worst case to notch.
Once in high school, the majority, instead of returning to the missed material, studies the “tower” with a bias in the specialty. The volume of formulas that came from above does not bother you at all.
Yes, the education system can be understood. The specialist is paid for the result, and not for what he knows from where the exhibitor in his calculations.
As a result, we do not come to conclusions, as mathematicians do. At the moment of the “leap of knowledge,” that is, when we discard a part of logical chains, the sacrament is decided. We take on faith what they tell us. The textbook turns into a scripture!
The prohibition of division by zero is the first and most intrusive ban on mathematics. Therefore, it is remembered for a lifetime. This is also a pedagogical problem that leaves an imprint on the whole of mathematics, as if on a “mystery covered in darkness”. This is a difficult problem, compared to it, to find the majority of the missing logical chains is not difficult.
You can turn a scripture back into a textbook. The reason for the ban should be strictly defined. The task of teachers to present it clearly. Science should not sow doubt.
2.2 What is division?
Captain Obvious asserts that to divide by zero you need to know what division is and what zero is. Sadly, Google suggests that many adherents of the "division by zero magic" do not even go through the first round of this hell. Namely, to understand what they are going to do and with what. Take a look at Wikipedia:
Division (division operation) is one of the four simplest arithmetic operations, the opposite of multiplication. Division is an operation that counts how many times one is contained in another.What follows from this:
- The division is not an independent operation. It is determined by multiplication . If you look at the definition of multiplication, it is determined by addition. Subtraction is also defined by addition. Addition independently and does not depend on anyone.
- There is no mention of zero in the definition. With the widespread prohibition of division by zero, it is very strange. By the way, there is no mention of zero in the definitions of the other arithmetic operations.
- The second part of the definition is not part of the definition, it is just an explanation. You can make sure by comparing with analogues in other trusted sources .
It seems that the most useful thing we have found here is the connection between operations. It can be said that division is the third spinning wine, multiplication and subtraction - the second, and addition - the first. Perhaps for this reason, the division began to fail when working with zero.
2.3 generating operations
So, only the addition operation contains a rule about how to determine the result of the operation (the sum) using two initial arguments (terms). All other arithmetic operations use this rule (matching numbers), but in addition impose their “additional conditions” .
Depending on the “additional conditions” arithmetic operations can be divided into direct and inverse :
- Direct operations: this is addition, multiplication and exponentiation. Expressing these operations through addition, all terms remain known. Determining the result of any of the operations is not difficult.
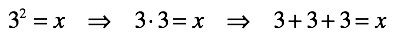
- Inverse operations: subtraction, division, taking the root (logarithm). These operations take the corresponding direct operation as a basis and “invert” it. Thus, expressing the operation through addition, at least one of the addends is unknown. This term is the result of the operation. The amount is usually known.
Determining the result of the operation, in general, the task is not trivial.
All direct operations have the same property. They are closed . That is, the type of result is completely determined by the types of input numbers (it is impossible to obtain a fractional result from the product of two integers).
Inverse operations are only partially closed (the value of the root of an integer can be an integer, or it may not). In those cases where the result fails, the operation is undefined . This problem has long been solved in a simple way: consider the resulting operation record and numbers as a new type of numbers:
.
Thus, we can say that the inverse operations and “generate” new types of numbers.
Mathematical language:
In general, the use of the term “inverse operation” is not acceptable to indicate the ability of an operation to generate new types of numbers. For example, “additional terms” can:The division is one of the generating operations. Perhaps something went wrong during the birth process and the newborn was injured. In order to answer this question, you need to understand where the division came from and where the zero came from.
- place the result of the operation in one or more terms (as shown in the example above);
- to determine the result of the operation as an answer to the question how many terms participated in the operation (fractional numbers, irrational numbers using the root);
- determine the result of the operation as the sum of an infinite number of terms. Moreover, all addends are known (Pi number and Euler number).
2.4 The evolution of arithmetic
Let us try to structure our understanding of arithmetic operations and the types of numbers they generate. For clarity, let us present one of the options, how the evolution of arithmetic can go.
2.4.1 Scope
We are in a cave. With the ability to count, no one was born. However, in the process of “contemplation”, an understanding emerged that such a concept is “quantity” . That is, we know that two mammoths and two apples have something in common and we can express this by bending our fingers. Accordingly, nothing but natural numbers at this stage we do not know.
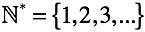
The set of natural numbers is marked with an asterisk “*” for uniqueness . Hereinafter, the absence of the concept of “zero” is emphasized.
There are several formal definitions of the sequence of natural numbers. We will take Peano's axiom as a basis. It is remarkable that these definitions were not described by the ancients. They appeared only in the 19th century, and after they passed the refinement procedure (in the original version there were nine, in the modern form already five).
Consider the formal definitions and their essence within our task (the traditional verbal description can be found on Wikipedia ):
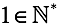
There is a number "one" and it is natural.
The following function is introduced S (x). For all positive arguments, it returns the next positive integer. In the first approximation (very rough), this is S (x) = x + 1, for example, 2 = S (1) and 3 = S (S (1)).
A clear prohibition is imposed on the global looping of the generated sequence of numbers. By generating numbers, we cannot get the element from which we started the generation, that is, one.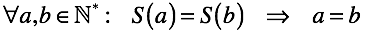
Different arguments of the following function should give different results. Thus, a clear ban on local looping is introduced. That is, the follow function should not re-generate a number that has already been generated.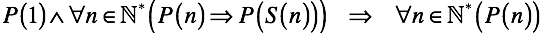
Mathematical induction , allowing to rise from the level of the elements of the sequence to the level of the sequence as a whole. If some statement “P” is true for the unit and for each pair of neighboring elements, then it is also true for all elements of the sequence.
For example. For numbers 2 and 3, it is true that between them there is one middle element 2.5, for 3 and 4 it is 3.5, etc. We conclude that between any neighboring natural numbers there is a middle element and it is the only one.
What conclusion can be drawn from these axioms? A ban on looping in any form (global or local) is introduced. A ban on looping always requires the following element. This is how the mathematical concept of "infinity" based on the concept of "quantity" appears. The concept of “infinity” cannot exist without the concept of “quantity”.
Mathematical language:
Quite often, the “starting element” in the Piano axioms takes zero. Why it is impossible to do this will be revealed when describing the operation “subtraction” (very soon).
The following function does not use the addition operation in the literal sense of the word. This is a fundamental function that is used both to build a set of natural numbers and for the formal definition of the operation of addition .
That is, both numbers and arithmetic operations are defined using the follow function.
The following function is included in the class of primitive recursive functions considered in the theory of algorithms . As you know, the concept of recursion does not contain the requirement of its finiteness (reachability of the terminal branches ), which means that it also implicitly defines the concept of “infinity”.
2.4.2 Addition
The first operation that occurred during our evolution. As whole fingers do not bend, the result will be whole. Is that the leader of the sum of the fingers may be a little more than all the rest. If your fingers are not enough, you can always call a scientific assistant in the cave and expand the bit grid.
2.4.2 Subtraction
On Thursday, hunters shot 12 mammoths. For Friday we ate 5 of them. How many mammoths are left?
The task is well solved by introducing the extension of the fingers. But the approach does not always work. For example, to estimate stocks for the weekend, the hunter bends seven fingers for the rest, straightens five fingers for Saturday (the rate of consumption per day) and “tries” to open it for Sunday.
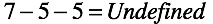
At this point, an “arithmeticException” occurs between “try” and “catch”. The result is not defined . Our operation is defined only for the case when the deductible is greater than the deductible.
However, the definition of subtraction does not impose any restrictions. To get rid of the requirement “a> b”, we introduce a “permutation rule” . That is, let us interchange the position of what is decremented and subtracted. But in order for the identity to remain true, the result needs to be marked with some sort of marker, for example, a minus sign. Any markers for mathematics are common (for example, the sign of the absence of zero in
).
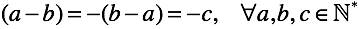
Due to the auxiliary operation “permutations” we came to the first abstraction - “ negative numbers ”. Marking in the form of a minus sign in a natural number is nothing more than a sign of deferred subtraction (but this is only for now).
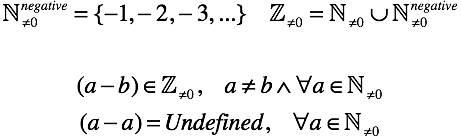
We have only one non-definite case, when the diminished and subtracted are equal. If we want to define it, then we will have to answer the question what is the concept of “nothing” . Although what all these difficulties are for, let us denote “nothing” by the symbol “0” (later we shall fully understand).
It remains to fix our decision in the form of “rules for addition / subtraction of zero” . They follow from the definition of zero after a couple of simple permutations:
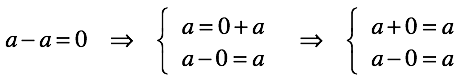
Let's see how well the rules entered. Solving equations, we can always find the unknown third from two known numbers. It does not matter in what part of the equation it is, the solution is always unique.
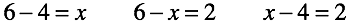
Negative numbers appeared as a result of the permutation, zero filled out “nothing”. Negative numbers and zero are born in different ways. Next, we will consider two branches of evolution: separately all numbers without zero and separately zero.
2.4.3 Multiplication
Multiplication is by definition a shortened record of addition. Multiplying the natural numbers, the result can only be natural. At this stage of evolution, the usefulness of the definition for us ends.
For negative numbers in the definition there is not a word about how to multiply them. These rules were formed gradually in the course of solving applied problems . In the modern interpretation, they are known as an addition to the multiplication in the form of “rules of signs” . They are defined so well that by applying them to non-zero integer numbers, the operation remains closed.
In the case of zero, the situation is radically different. One more rule is introduced: “the rule of multiplication of zero“ (multiplication of any number by zero gives zero). But this rule only seems new. We cannot introduce any other rule. The definition of multiplication strictly connects us with addition. Expanding multiplication through addition, we use the “rules of addition / subtraction of zero,” respectively, we can get nothing but zero.
Mathematical language:
If we compare the operations of addition and multiplication in arithmetic and general algebra, we can notice one serious difference. In arithmetic, these operations are related by definition. Distributive law is a consequence of these definitions. In general algebra, on the contrary, operations are described independently of each other, and already in the definition of a field (rings, to be more precise) are associated by distributional law. Consequently:
The field, the crown of universality, “behind the ears” is drawn to elementary arithmetic. But to get rid of this support (to describe the requirements for operations symmetrically) it is necessary to expand the definition of the distribution law (starting from the ring of course). There is reason to believe that another algebraic system may become the culmination of universality, for which the field will be a particular case.
- In the definition of the field there is a requirement for the inverse element. In addition, for multiplication and addition, the requirement is described not symmetrically. The absence of the inverse element by multiplication for neutral elements by addition is allowed, but not vice versa.
- To give symmetry in the description of the wheels, we had to abandon the usual distribution law, and therefore from operating the field.
2.4.4 Division
Division is the inverse operation of multiplication. In equations with positive and negative numbers, it becomes possible to substitute non-multiple numbers.
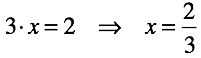
As a consequence, the operation generates rational numbers .
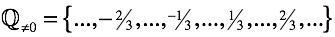
To inscribe them in arithmetic, the set includes “rules for actions with ordinary fractions” . Fortunately, these rules harmoniously coexist with the “rules of signs” that we introduced earlier. As a result, it is still possible in equations to determine the unknown with any arrangement using two known numbers.
In the case of zero, it can be multiplied by rational numbers. That's all, the harmony is over! For only two of the three types of equations with arbitrary numbers, a solution can be found.
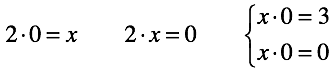
First, it became possible to make an equation with numbers that are not so convenient that we cannot find a single solution. The solution is “not possible.”
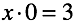
Secondly, the opportunity to make an equation in which there is an infinite number of solutions. It is also impossible to choose one of them. The solution is “not unique”.
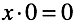
It is easy to guess, the root of the problem of division by zero lies in the “impossibility” and “ambiguity” of multiplying zero. Multiplication, in turn, retransmits the “addition / subtraction zero rules”. In fact, you can set equations that have the same properties, using only addition.
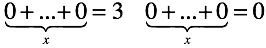
In both equations, you need to determine the number of zeros that you need to add to get an arbitrary number or zero.
The division did not bring something qualitatively new. There was a transformation of the "impossibility" and "ambiguity" of addition to concrete entities , in the form of uncertainty 1/0 and 0/0, respectively.
It turns out that the division, as the first suspect, is not to blame for the fact that it is impossible to divide by zero.
As long as the concept of “zero” does not exist, all operations, including exponentiation and taking the root (logarithm), are well closed (already true on complex numbers) and arithmetic works great. But there is one “but”, with this configuration of arithmetic, the subtraction operation turns out to be not fully determined.
After introducing zero, addition and subtraction work well. For other operations, it is more likely to install crutches (
) than an equal number.
2.5 What is zero?
So, since the division operation was not to blame for the prohibition of division by zero. Then let's try to put together everything that we know about zero:
- The need for zero appeared in the definition of the subtraction operation.
- “ ”. , , “ ”. “ ” , . , “” .
( ) “ ” . , “” , . , , .
- “”, “” ( ). “” , “ ” “”. , , “” “”. , .
.
, , , , . . () . ( ) . . , .
- - “” “” “” . .
- , . , , “ / ” . , , . , .
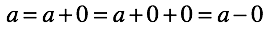
On the last point it is worth staying in more detail. Let's try to present not an absolute zero.
Suppose we have a mammoth. For its transportation need packaging. If you put a mammoth in a container, and then pull it out, then the container will be “nothing” (just like in the picture with the match above). However, the packaging for two mammoths is somewhat different from the packaging for one. In the case of theft, there is reason to charge in accordance with the size of the remaining container. So, there are situations when one “nothing” to another “nothing” is different.
Can “nothing” be different or “nothing” is a single and absolute essence? This is a question that cannot be answered . The debate on whether there is a God is analogous and meaningless, but is it one or many of them. The answer in this world, we will not know.
Mathematical language:
:Thus, at the very bottom of arithmetic, where there is neither natural numbers nor addition (and therefore other operations), there is zero.
- . , . , . , :
- . . , , . ( ) :
. . .
. .
- Theory of Algorithms . You can look into arithmetic even deeper. To build a sequence of natural numbers and define the operation of addition, the class of primitive recursive functions is used . The function of following S (x), is used in Peano's axioms, one of them. Along with it, the Zero function O (x) is defined , a function that always returns zero.
Well, the answer to the question of how many zeros should be arithmetic cannot give. We use one zero. In the wheels considered in the first part, arithmetic with an infinite number of zeros was used. And can there be a finite number of zeros, but more than one.
Maybe such arithmetic successfully used. One of the clearest examples of arithmetic with “signed zero” , implemented in JavaScript.
Mathematical language:
The sign zero, although written similarly to +0 and -0, has nothing to do with the infinitesimal calculus .However, this arithmetic also suffers from uncertainties.
Introducing the sign zero is another option for expanding the number line. In the general topology there is a very close (but not identical) space “ line with two origins ” (not Hausdorff).
Javascript example
console.log(+0) => 0 console.log(-0) => -0 console.log(-0 === +0) => true console.log(0-0) => 0 console.log(-0-0) => -0 console.log(0/0) => NaN console.log(-0/0) => NaN console.log(-0/-0) => NaN console.log(Infinity/Infinity) => NaN console.log(-Infinity/Infinity) => NaN console.log(-Infinity/-Infinity) => NaN console.log(Infinity — Infinity) => NaN console.log(Infinity + Infinity) => Infinity It can be concluded that uncertainties in arithmetic will persist as long as the number of zeros is finite.
By and large, it does not matter how we treat zero. Do we need a single and absolute zero, and maybe a couple or an infinite number, arithmetic can always adjust to us.
2.6 Our infinity is everything
Finally, I would like to present at least one version of a numerical axis containing an infinite number of zeros (this example describes the concept and does not pretend to mathematical rigor).
For subtraction, when reducing and subtracting are equal, instead of entering zero we define the operation of “reduction”. That is, we allow deleting equivalent expressions with the opposite sign. But if we have reduced everything, then the result is no longer suitable for further use.
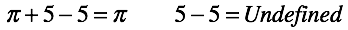
We start counting in the number axis from one (from the first number of the concept “quantity”). To generate the remaining numbers, we use the infinite sequence defined by the following function (it is also used in Peano's axioms ). This will be our reference generator of infinite sequence.
To get a very small number using the follow function, you need to expend as much force as on the generation of a very large one. We use the functions f (x) = 1 / x and f (x) = x. The task is not worth giving the decimal form a rational fraction, respectively, the computational complexity of the functions is the same.
Since neither “absolute zero” (marked with a zero symbol), nor “potential infinity” (marked with an unsigned infinity symbol) are unattainable, the axis grows from one infinitely in both directions (non-uniform scale).
When defining subtraction, a “permutation rule” is defined. We, in turn, make a copy of our direct and display it mirror. Twin numbers and unreachable limits are marked with a minus sign. Positive line, not connected with negative. The transition from one straight line to another is performed only by the “permutation rule”.
For clarity, we depict the resulting numerical line in the form of a circle. Just as we did with the projective extension. However, the limit values are not closed (we do not compactify). This transformation of the semantic load does not carry and is performed only to improve perception.
Now we are ready for the most important thing. Let us make the transition from a single potential infinity to an infinite set of actual infinities (a similar approach is used in non-standard analysis ).
We will treat infinitely large quantities as full numbers. For the reference actual infinity, we take the “speed” at which the following function reaches any arbitrary number. We denote this number
. Not to be confused with potential infinity. She is still unattainable.
To obtain various actual infinities, we will use the notion of the limit of a function when tending to the number
. We will not reject infinitesimally (of lower order) and will not absorb constants with infinitely large quantities, as is customary in classical analysis. We will save all the information component number. Accordingly, we have the opportunity to compare infinitely large numbers.
Raising the number
to negative degrees, we get infinitely small numbers. In fact, this is our infinite set of zeros, which can be compared with each other and used in arithmetic (as opposed to an infinitely small value in classical analysis).
Mathematical language:
From the point of view of general algebra, our algebraic system is not a field, since there is no zero (neutral element). Non-standard analysis operates with similar actual infinities, they are called hyperreal numbers . Zero (neutral element) is one of the hyperreal numbers. Accordingly, the algebraic system of nonstandard analysis operates with a field.
Our reference infinity
In fact, the limits practically cease to be simplified, in the form to which we are accustomed. Now we just replace the variable with
If there is a practical need, we can define a subtraction operation and for equal numbers (instead of the “reduction” defined by us above). For example, it may be a lower order number than the original numbers.
(analogue of the equation of the wheel ). Arithmetic will be closed. But you need to be aware that the sum of two twos will immediately be equal to four with a tail. This is somewhat similar to the addition of speeds in the theory of relativity . Another example is thermodynamics and the concept of absolute zero temperature . Having stopped molecules, atoms continue to move. Having stopped atoms, quarks are still moving, etc. Immersion is infinite.
Epilogue
We are between the past and the future, between the micro and macro world. In all areas, sooner or later we find a limit beyond which we can not go and this is normal.
In math it's not like that. We are told that zero is a number. Then put it on par with all the other numbers. Then we are told that the length of the path from minus one to one is two. And at this moment our consciousness finally dissolves zero among the other numbers.
We cannot divide by zero, because we have forgotten that once the notion of “nothing” and the notion of “quantity” were mixed.
Useful literature
- F. Klein: Elementary Mathematics from a Higher Point of View ( pdf )
- V.Uspensky: What is a non-standard analysis? ( pdf )
- Setzer, Anton (Drafts): Wheels, 1997 ( pdf )
- JJO'Connor and EFRobertson: A history of Zero ( html )
- Y. Lebedev: Mathematics of infinity ( html )
- http://en.wikipedia.org/wiki/Undefined_(mathematics)
- https://ru.wikipedia.org/wiki/Nonstandard_analysis
Source: https://habr.com/ru/post/249431/
All Articles