On the existence of periodic solutions in the Lorentz system

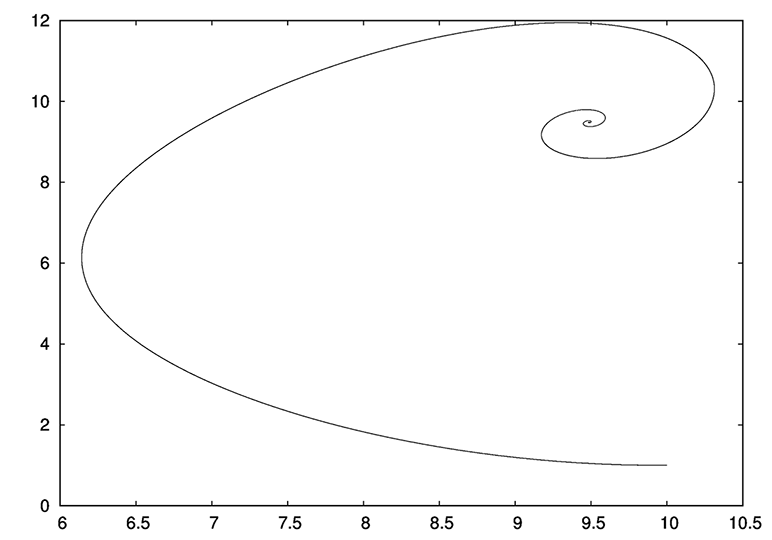
This is my third topic on Habré ( part 1 and part 2 ), dedicated to the dynamic system of Lorentz. I continue to study the question of the existence of periodic solutions (cycles) in this system. It was possible to get an interesting result with a certain ratio of its parameters.

Consider the system of differential equations of Lorentz

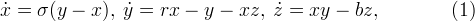
Where 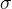, r and b - some positive numbers, system parameters.

Prove that if 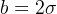, then in system (1) there are no periodic solutions (except, of course, equilibrium positions).
')
Make a replacement

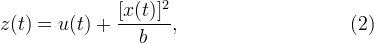
Where 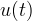- some function of time.

Differentiate (2), we get


In the left side of expression (3) we substitute the right side of the third equation of system (1), and in the right side of (3) - the right side of the first equation of system (1), given that 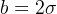. Will get


Instead of z in (4) we substitute the expression (2), whence we have the equation

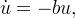
whose solution is the function

Where 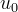- arbitrary constant.

Now in the second equation of system (1) we substitute the expression (2) instead of z . In this case, we express y from the first equation of system (1). Will get

and


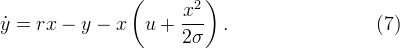
Substituting (5) and (6) into (7), we have


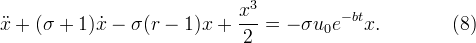
Consider the non-autonomous case where 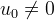in equation (8). Suppose that in this case, equation (8) has a periodic solution with period T. Since the derivative of a periodic function with period T is a periodic function with period T , the left side of equation (8) is a periodic function with period T. However, the right side of equation (8) is non-periodic, since 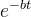not a periodic function. Got a contradiction.

Thus, with 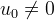equation (8) has no periodic solutions.

Consider now the case when . We have an autonomous second order equation

whose criterion is Bendixon [1, p. 142-143] there are no periodic solutions, which proves their absence in the Lorentz system with .

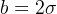Note that in this case the parameter r can take any values. Then, for sufficiently large values ​​in the Lorentz system, there will also be no periodic solutions, which seems very obscure, since the parameter r is proportional to the temperature difference between the lower and upper liquid layer during free convection. With an increase in the temperature gradient in the layer, convective shafts should appear in the fluid, and here the fluid eventually comes to a stationary state (laminar mode). This is confirmed in the numerical experiment (stable foci were observed for different values ​​of r — a drawing (projection of the arc of the trajectory on the xOy plane) at the beginning of the topic). Most likely, this is explained by the fact that the Lorentz system rather rudely describes this process, although with different ratios between 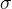and b ( r takes a sufficiently large value) in system (1) a stable limit cycle is observed [2, p. 291-294].

Despite all the simplicity, in my opinion, this result from the point of view of the theory of differential equations is interesting because the nonlinear third-order system allowed a decrease in order, which rarely happens, and the theory of differential equations on the plane is rather well developed.

Consider another case where 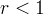. In the literature known to me, it is investigated in a linear approximation. Let's apply the second Lyapunov method. Let's make Lyapunov's function

having properties:

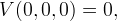
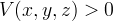for
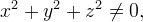
at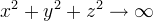
and
for 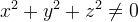by virtue of the right sides of the equations of system (1). Then, by the Barbashin-Krasovsky theorem [3, p. 248-250] any system solution (1)
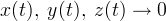at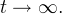

A more general case is described in [4] (Lemma 1.2), where it is proved that there are no cycles in system (1) (limit modes — equilibrium positions) for
and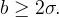

Also note that system (1) always has particular solutions of the form

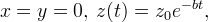
Where 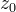- arbitrary constant.

In this topic, the issue of the system (1) lacking periodic solutions was considered. However, analytical studies of the dynamics of system (1) for the presence of cycles are described in the literature, but not so many sources, since many study the Lorentz system numerically. The following is a list of references where it was possible to find a rigorous proof of the existence of a limit cycle in system (1) for large values ​​of the parameter r [2, 4–8]. It includes the manuscript [4] of Viktor Yudovich Yosovich (unpublished earlier in scientific journals), where this issue is covered in detail.

Literature

1. Nemytsky V.V., Stepanov V.V. Qualitative theory of differential equations. - M .: Editorial URSS, 2004.
2. Neimark Yu.I., Landa PS Stochastic and chaotic oscillations. - M: LIBROCOM, 2009.
3. Demidovich B.P. Lectures on the mathematical theory of sustainability. - M .: Science, 1967.
4. Yudovich V.I. Asymptotics of the limit cycles of the Lorentz system for large Rayleigh numbers // Manuscript dep. in VINITI, №2611-78. 1978
5. Robbins KA Periodic Solutions and Bifurcation Structure at a Rowing Model // SIAM Journal on Applied Mathematics, 36 (3): 457-472, 1979.
6. Shimizu T. Analytic form of the Simplest Limit Cycle in the Lorenz Model // Physica A: Statistical Mechanics and its Applications, 97 (2): 383-398, 1979. 4
7. Pokrovsky L.A. Solution of the system of Lorentz equations in the asymptotic limit of a large Rayleigh number. I. The Lorentz system in the simplest quantum laser model and the application of the averaging method to it // Theoretical and Mathematical Physics, 62 (2): 272-290, 1985.
8. Jibin Li, Jianming Zhang. New Treatment on Bifurcations of Periodic Solutions and Homoclinic Orbits in the Lorenz Equations // SIAM Journal on Applied Mathematics, 53 (4): 1059-1071, 1993