Non-von Neumann computer based on combinatorial logic
Hello. In this article I will talk about my non-von Neumann computer hobby project. The architecture corresponds to the functional paradigm: the program is a tree of applications of elementary functions to each other. Iron is a homogeneous static network of primitive nodes, onto which the dynamic tree of the program is projected, and over which the program “creeps” by computing.

This is how a tree works, only here an arithmetic expression is calculated for clarity, not a combinatorial one; The step in the figure is one machine cycle.
Now ready for an early prototype, existing in the form of a tactical software simulator, and in the form of implementation on the FPGA.
Traditional architecture computers have changed the world, but a period of incredible, intoxicating growth has apparently ended. One of the main limiting factors is the bottleneck between the processor and memory, which prevents parallelization. Functional programming is an attractive direction for avoiding the limitations of the Neumann, centralized architecture, but attempts to create a computer architecture based on a functional approach have not been successful .
')
But as time goes on, microelectronics technology is improving and becoming more democratic. I try to make my computer based on combinatorial logic . The computational problem is formulated as an expression - a tree of applications of combinator functions to each other:
Program execution is understood as the transformation of this expression into some simple form that gives an answer. The system is Turing-complete, which has a downside: not every expression can be calculated. For more information on how to calculate something using combinatorial logic, see here and here .
The main idea is to place the program tree on a hardware tree of cells capable of applying combinators.
Why hardware tree? The fact is that when we project a program tree onto a one-dimensional address space we are used to, non-local, “long” connections inevitably arise. Here is an example of a flat tree entry: "(A * B) + (C * D) - E" Here "+" is the source of the data for "-", but they are separated in the formula.

Non-intersecting subtrees can be calculated independently and simultaneously, hence natural concurrency. There is no shared memory: the data is stored locally, which means there is no throat “processor - bus - memory”. All operations, except copying subtrees, are performed quickly. In my previous article, I showed how you can use a tree of such a structure to sort numbers.
So, we have a tree of applications of some functions to others,
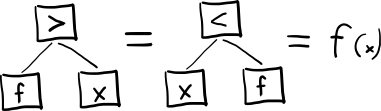
where leaves are elementary functions, in the case of combinatorial logic these are basic combinators, for example, the set S, K, I:
The syntax for the assembler will be borrowed from the unlambda esoteric functional programming language (as promised in this publication, at the very end ):
This solution allows the use of the unlambda interpreter to verify the correctness of the calculations.
Here is a stroke (`) symbol of the function application. A prefix notation is used, that is, `fx = f (x).
F (G (X, Y), H (Z, V)) = `` F``GXY``HZV
In this form, the expression is fed to the input of the machine. The download takes place through the root of the tree, the external device symbolically transfers the program to the root node, which the first character picks up for itself, and transfers the rest to its descendants, each of which performs the loading procedure recursively. Having received the subtree completely, the node reports this to the ancestor and begins to execute its part of the program.
For example, let's calculate the Boolean expression, "(1 | 0) & (0 | 1)" . In the combinatorial basis, this can be represented as `` `` ssk````siik`ki````sii`kik Yes, such expressions are impossible to read, but they can be written, see the textbook . As a result of executing a program of this type, the state of the machine will evolve from the original formula to a single boolean value, either “1” , encoded as “k” , or the value “0” in the form of `` ki ' . For this particular formula, we get exactly “k” .
The calculation takes 116 cycles. Of these, the first 67 bars continue to load the program. From the point of view of practical utility, the figures are not encouraging, but there is potential for optimization, for example, using a richer set of combinators will reduce the size and runtime of the program.
The described results were obtained on a software simulator. Sources and executable file for win here . The simulator is a console application, does not require installation, the combinatorial expression is passed as a command line parameter.
The simulator exactly corresponds to the FPGA version implemented in the verilog, but with one fundamental difference - it is not limited in physical resources. That is, the simulator has a potentially infinite tree, and on FPGA the tree is limited. A tree of 63 knots, that is, a depth of 6, occupies 16,000 Altera LE, which is a lot; if the program grows more in the course of the calculation, the calculations end in failure. The only benefit from the hardware version is to show the principle realizability in hardware.
Let's return to the calculations. Now we calculate the arithmetic expression, (2 + 1) . To translate this into the language of combinatorial logic, we use the Church numerals. We get the expression `` `` si`k`s``s`kski`````` To get something meaningful, we substitute this expression like this: `` (2 + 1) ki . Calculating this we get `k`k`ki , the number of letters k symbolizes the answer received. The calculation takes 124 clocks. But the calculation of `` (1 + 2) ki takes already 243 clocks, `` (3 + 3) ki 380 clocks. Alas, while everything is very slow, below I have marked the path to acceleration.
The examples given are simple, unconditionally “collapsing” expressions, in practice such tasks are better performed by a traditional machine. However, combinatorial logic being a Turing complete system, allows solving problems of greater computational complexity, the corresponding expressions can grow in the course of calculation. True, this property brings the risk of unrestrained growth or even a never-ending program, but the advantage the proposed architecture can only show on such tasks. Here in the description there are cycles and recursion, the classic construction for their organization, the fixed point combinator:
`Yx =` x`Yx = `x`x`Yx =` x`x`x`x ...
Y (x) = x (Y (x)) = x (x (x (x (...))))
The above two simple examples show that Boolean calculations look more interesting than arithmetic, the machine is very sensitive to the size of objects. But the calculation of Boolean expressions in itself is not very promising: the task, even on a sequential machine, is performed in O (1), that is, the program will load longer than it is executed.
This “flaw” is devoid of the SAT task. Here we have a boolean expression complemented by variables, and it is necessary to determine whether the formula holds; This is an NP-complete problem. You can achieve significant acceleration by simultaneously checking several sets of variable values. It is to this type of tasks I now look at. Interesting problems with unpredictable branches and without large numbers, such as symbolic calculations and automatic proof of theorems.
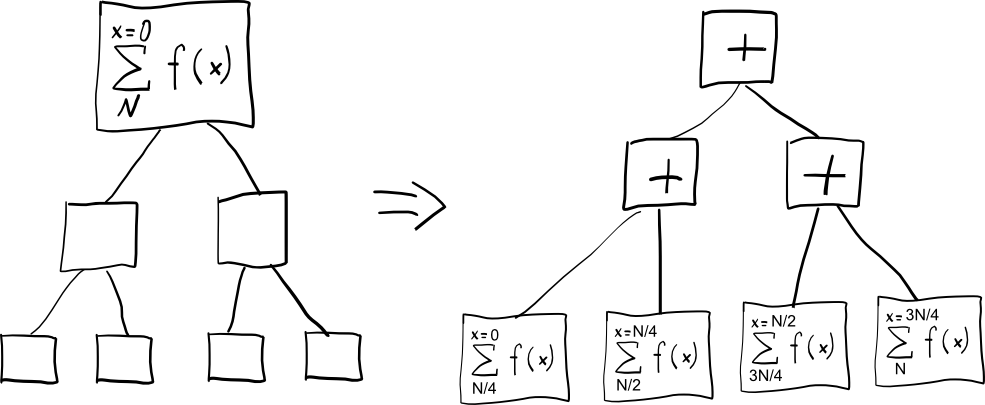
The ideal task should be formulated with a small expression that first grows like a tree from a seed, forming as many parallel branches as possible and then roll back, combining the results from the branches, something like micro MapReduce:
There is one more direction of possible applications: reconfigurable calculations . The idea is this: to supplement the alphabet of the machine with special blocks that are not combinators, but carry a special meaning external to the language. Work in two phases, the combinatorial machine works in the first phase. During the execution of the program, all the combinators must calculate, and only the special blocks remain, which form some desired structure, which (in the second phase) will perform the target work.
For example, if we take logical elements as special blocks, we can obtain a dynamic FPGA, which, on request, will generate, on the fly, say, a multiplier by the required constant or adder of the calculated width from the parameterized adder circuit.

We did almost the same thing above, when we applied the Churchill number (3 + 3) to the combinators k and i , which were not executed (as functions) in the calculation process, but served to visualize the result. Replacing k with a one-bit adder, we would get a conditional digit adder 6 by the time the calculations were completed.
This potential application is not so demanding on performance, provided that reconfiguration is required not too often.
Since the functional program tree is rather sparse, laying it on a balanced static binary tree is very disadvantageous. Therefore, in the near future, the transition to a hardware dynamic tree that will live on a regular graph, working on the principle of a cellular automaton .
But any graph is finite, and many functional expressions tend to grow indefinitely, especially with vigorous execution ; This is another problem that needs to be addressed in the future. Now, rather, an energetic rather than lazy computation strategy is used, it will probably have to be modified, but in order to do this, you need to find a model problem that is close to practical one.
A certain benefit in terms of optimization can be obtained by expanding the set of hardware-implemented combinators, the basic set of SKI is now used, other combinators may be useful, including
There is no input-output per se, the answer is given by the program body itself, transformed during execution. Thoughts as it was possible to realize IO is, but for now this task is not my priority.
Now the machine uses the transfer of parameters by value, which leads to the need to copy the arguments, in fact, most of the time the machine is engaged in copying. It would be tempting to implement the transfer by reference, the program interpreter takes the efficiency of such a transition by several orders of magnitude! How to implement this on the hardware network of nodes, I still have little idea, but when there is an indicative practical task, I intend to seriously deal with this.
Another function that potentially extends the capabilities of the machine is hardware pattern matching, in particular, testing subtrees for equality.
Increasing the level of programming is also in the list of priorities, while all forces are going to improve the simulator.
The more successful sister of combinatorial logic is lambda calculus. Is it possible to modify the computational tree for this version of functional programming? I guess, yes. The main trouble is that we have a potentially infinite number of variable names, which means that a variable call cannot be placed on one hardware node (final). But it can be solved; in principle, it is possible to switch to lambda calculus, as a more popular model. I stopped at combinatorial logic, as combinators are more elegantly projected on operations with subtrees.
I adopted the idea of creating a specialized calculator of functional programs from my supervisor, Vadim Nikolaevich Falk, when I studied at the MIREA postgraduate a dozen years ago. The scientific work of the team focused on theoretical studies in the field of functional and functional logic programming. In particular, Falk developed the Falgol language, a kind of functional assembler. It was positioned for theoretical and computational purposes, such as proving the correctness of programs, but there were also attempts to build a computer based on it.
I did a little bit different and didn’t really succeed, to be honest, but the idea to create a functional-logical calculator sown and after 10 years did sprout. All this time, I worked as a system programmer in a company developing iron, including microcircuits, which allowed me to master the basics of digital circuitry, and bring it to a hardware prototype.
The project is progressing. It was possible to create a prototype not the background of the Neumann computer combining the features of several interesting paradigms: functional programming, cellular automata; analogues are not known to me. The FPGA-variant is so far not very useful due to the limitations in capacity, but a software simulator that exactly corresponds to the hardware model makes it possible to study the execution of programs. There is no talk about practical use in the current form, but I'm already looking for a model task that will be taken as a goal for the future use of the machine.
Finally, I note once again that modern development of electronics makes it possible to implement very non-trivial ideas, although this is a laborious task. Thanks for attention.
RV Dushkin aka darkus "Combinators are easy"
David Madore "The Unlambda Programming Language"
Unlambda language interpreter

This is how a tree works, only here an arithmetic expression is calculated for clarity, not a combinatorial one; The step in the figure is one machine cycle.
Now ready for an early prototype, existing in the form of a tactical software simulator, and in the form of implementation on the FPGA.
Ideology
Traditional architecture computers have changed the world, but a period of incredible, intoxicating growth has apparently ended. One of the main limiting factors is the bottleneck between the processor and memory, which prevents parallelization. Functional programming is an attractive direction for avoiding the limitations of the Neumann, centralized architecture, but attempts to create a computer architecture based on a functional approach have not been successful .
')
But as time goes on, microelectronics technology is improving and becoming more democratic. I try to make my computer based on combinatorial logic . The computational problem is formulated as an expression - a tree of applications of combinator functions to each other:
// ( ) 2+3 = + 2 3 = + ( +1 1 ) ( +1 1 1 ) = + ( +1 1 ) ( +1 +1 1 ) `` ``si`k`s``s`ksk ``s``s`ksk i ``s``s`ksk ``s``s`ksk i Program execution is understood as the transformation of this expression into some simple form that gives an answer. The system is Turing-complete, which has a downside: not every expression can be calculated. For more information on how to calculate something using combinatorial logic, see here and here .
Architecture
The main idea is to place the program tree on a hardware tree of cells capable of applying combinators.
Why hardware tree? The fact is that when we project a program tree onto a one-dimensional address space we are used to, non-local, “long” connections inevitably arise. Here is an example of a flat tree entry: "(A * B) + (C * D) - E" Here "+" is the source of the data for "-", but they are separated in the formula.

Non-intersecting subtrees can be calculated independently and simultaneously, hence natural concurrency. There is no shared memory: the data is stored locally, which means there is no throat “processor - bus - memory”. All operations, except copying subtrees, are performed quickly. In my previous article, I showed how you can use a tree of such a structure to sort numbers.
So, we have a tree of applications of some functions to others,

where leaves are elementary functions, in the case of combinatorial logic these are basic combinators, for example, the set S, K, I:
Ix = Ix = x - Kxy = (Kx)y = x - Sxyz = ((Sx)y)z = (xz)(yz) - SKI on hardware tree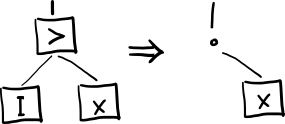





The syntax for the assembler will be borrowed from the unlambda esoteric functional programming language (as promised in this publication, at the very end ):
`ix = Ix ``kxy = (Kx)y ```sxyz = ((Sx)y)z This solution allows the use of the unlambda interpreter to verify the correctness of the calculations.
Here is a stroke (`) symbol of the function application. A prefix notation is used, that is, `fx = f (x).
F (G (X, Y), H (Z, V)) = `` F``GXY``HZV
In this form, the expression is fed to the input of the machine. The download takes place through the root of the tree, the external device symbolically transfers the program to the root node, which the first character picks up for itself, and transfers the rest to its descendants, each of which performs the loading procedure recursively. Having received the subtree completely, the node reports this to the ancestor and begins to execute its part of the program.
Work examples
For example, let's calculate the Boolean expression, "(1 | 0) & (0 | 1)" . In the combinatorial basis, this can be represented as `` `` ssk````siik`ki````sii`kik Yes, such expressions are impossible to read, but they can be written, see the textbook . As a result of executing a program of this type, the state of the machine will evolve from the original formula to a single boolean value, either “1” , encoded as “k” , or the value “0” in the form of `` ki ' . For this particular formula, we get exactly “k” .
The calculation takes 116 cycles. Of these, the first 67 bars continue to load the program. From the point of view of practical utility, the figures are not encouraging, but there is potential for optimization, for example, using a richer set of combinators will reduce the size and runtime of the program.
Simulator and FPGA version
The described results were obtained on a software simulator. Sources and executable file for win here . The simulator is a console application, does not require installation, the combinatorial expression is passed as a command line parameter.
A brief description of the simulator window in interactive mode.
1) Program at the entrance
2) The current state of the program as text
3) Full state of hardware tree
4) Deciphering the status of the current node

1) Program at the entrance
2) The current state of the program as text
3) Full state of hardware tree
4) Deciphering the status of the current node
Here is a small video demonstration
The simulator exactly corresponds to the FPGA version implemented in the verilog, but with one fundamental difference - it is not limited in physical resources. That is, the simulator has a potentially infinite tree, and on FPGA the tree is limited. A tree of 63 knots, that is, a depth of 6, occupies 16,000 Altera LE, which is a lot; if the program grows more in the course of the calculation, the calculations end in failure. The only benefit from the hardware version is to show the principle realizability in hardware.
Let's return to the calculations. Now we calculate the arithmetic expression, (2 + 1) . To translate this into the language of combinatorial logic, we use the Church numerals. We get the expression `` `` si`k`s``s`kski`````` To get something meaningful, we substitute this expression like this: `` (2 + 1) ki . Calculating this we get `k`k`ki , the number of letters k symbolizes the answer received. The calculation takes 124 clocks. But the calculation of `` (1 + 2) ki takes already 243 clocks, `` (3 + 3) ki 380 clocks. Alas, while everything is very slow, below I have marked the path to acceleration.
The examples given are simple, unconditionally “collapsing” expressions, in practice such tasks are better performed by a traditional machine. However, combinatorial logic being a Turing complete system, allows solving problems of greater computational complexity, the corresponding expressions can grow in the course of calculation. True, this property brings the risk of unrestrained growth or even a never-ending program, but the advantage the proposed architecture can only show on such tasks. Here in the description there are cycles and recursion, the classic construction for their organization, the fixed point combinator:
`Yx =` x`Yx = `x`x`Yx =` x`x`x`x ...
Y (x) = x (Y (x)) = x (x (x (x (...))))
Hypothetical use of the combinatorial machine in practice
Logical conclusion
The above two simple examples show that Boolean calculations look more interesting than arithmetic, the machine is very sensitive to the size of objects. But the calculation of Boolean expressions in itself is not very promising: the task, even on a sequential machine, is performed in O (1), that is, the program will load longer than it is executed.
This “flaw” is devoid of the SAT task. Here we have a boolean expression complemented by variables, and it is necessary to determine whether the formula holds; This is an NP-complete problem. You can achieve significant acceleration by simultaneously checking several sets of variable values. It is to this type of tasks I now look at. Interesting problems with unpredictable branches and without large numbers, such as symbolic calculations and automatic proof of theorems.
The ideal task should be formulated with a small expression that first grows like a tree from a seed, forming as many parallel branches as possible and then roll back, combining the results from the branches, something like micro MapReduce:

Reconfigurable computations
There is one more direction of possible applications: reconfigurable calculations . The idea is this: to supplement the alphabet of the machine with special blocks that are not combinators, but carry a special meaning external to the language. Work in two phases, the combinatorial machine works in the first phase. During the execution of the program, all the combinators must calculate, and only the special blocks remain, which form some desired structure, which (in the second phase) will perform the target work.
For example, if we take logical elements as special blocks, we can obtain a dynamic FPGA, which, on request, will generate, on the fly, say, a multiplier by the required constant or adder of the calculated width from the parameterized adder circuit.

We did almost the same thing above, when we applied the Churchill number (3 + 3) to the combinators k and i , which were not executed (as functions) in the calculation process, but served to visualize the result. Replacing k with a one-bit adder, we would get a conditional digit adder 6 by the time the calculations were completed.
This potential application is not so demanding on performance, provided that reconfiguration is required not too often.
Directions of development, problems and their possible solutions
Efficient use of nodes
Since the functional program tree is rather sparse, laying it on a balanced static binary tree is very disadvantageous. Therefore, in the near future, the transition to a hardware dynamic tree that will live on a regular graph, working on the principle of a cellular automaton .
Something like that, on the left, an expression, on the right, its laying on a hypothetical apparatus

But any graph is finite, and many functional expressions tend to grow indefinitely, especially with vigorous execution ; This is another problem that needs to be addressed in the future. Now, rather, an energetic rather than lazy computation strategy is used, it will probably have to be modified, but in order to do this, you need to find a model problem that is close to practical one.
Command system expansion
A certain benefit in terms of optimization can be obtained by expanding the set of hardware-implemented combinators, the basic set of SKI is now used, other combinators may be useful, including
Bxyz = x(yz) - y Cxyz = xzy - , Wxy = xyy - , Yx = x(Yx) - . (+1)nfx = f(nfx) - There is no input-output per se, the answer is given by the program body itself, transformed during execution. Thoughts as it was possible to realize IO is, but for now this task is not my priority.
Now the machine uses the transfer of parameters by value, which leads to the need to copy the arguments, in fact, most of the time the machine is engaged in copying. It would be tempting to implement the transfer by reference, the program interpreter takes the efficiency of such a transition by several orders of magnitude! How to implement this on the hardware network of nodes, I still have little idea, but when there is an indicative practical task, I intend to seriously deal with this.
Another function that potentially extends the capabilities of the machine is hardware pattern matching, in particular, testing subtrees for equality.
Increasing the level of programming is also in the list of priorities, while all forces are going to improve the simulator.
About lambdas
The more successful sister of combinatorial logic is lambda calculus. Is it possible to modify the computational tree for this version of functional programming? I guess, yes. The main trouble is that we have a potentially infinite number of variable names, which means that a variable call cannot be placed on one hardware node (final). But it can be solved; in principle, it is possible to switch to lambda calculus, as a more popular model. I stopped at combinatorial logic, as combinators are more elegantly projected on operations with subtrees.
Prehistory
I adopted the idea of creating a specialized calculator of functional programs from my supervisor, Vadim Nikolaevich Falk, when I studied at the MIREA postgraduate a dozen years ago. The scientific work of the team focused on theoretical studies in the field of functional and functional logic programming. In particular, Falk developed the Falgol language, a kind of functional assembler. It was positioned for theoretical and computational purposes, such as proving the correctness of programs, but there were also attempts to build a computer based on it.
I did a little bit different and didn’t really succeed, to be honest, but the idea to create a functional-logical calculator sown and after 10 years did sprout. All this time, I worked as a system programmer in a company developing iron, including microcircuits, which allowed me to master the basics of digital circuitry, and bring it to a hardware prototype.
Conclusion
The project is progressing. It was possible to create a prototype not the background of the Neumann computer combining the features of several interesting paradigms: functional programming, cellular automata; analogues are not known to me. The FPGA-variant is so far not very useful due to the limitations in capacity, but a software simulator that exactly corresponds to the hardware model makes it possible to study the execution of programs. There is no talk about practical use in the current form, but I'm already looking for a model task that will be taken as a goal for the future use of the machine.
Finally, I note once again that modern development of electronics makes it possible to implement very non-trivial ideas, although this is a laborious task. Thanks for attention.
Links
RV Dushkin aka darkus "Combinators are easy"
David Madore "The Unlambda Programming Language"
Unlambda language interpreter
Source: https://habr.com/ru/post/249413/
All Articles