Features of domain modeling using OOP

Introduction

I want to note that it will be very difficult for those who use OOP terms to understand me. The fact is that the PLO has replaced the concept. In the PLO, a class is not understood as a set, as is customary in mathematics or linguistics. In OOP, a class is called a type of objects , as in Aristotle. It would be correct in OOP instead of the term object class to use the term object type . Once, having moved away from the correct terminology, it is very difficult to return to the fold of correct terms. In this article I will try to help those who want to deal with the terminological porridge, brewed by the PLO. In my reasoning, I will use the terms in their original sense, and not in the sense of the PLO. The term class will be taken from the logical paradigm of modeling domain domains, which, in turn, borrowed this term from set theory. The terms type and instance will be taken from the theory of types, built on the paradigm of Aristotle on the existence of types.

It is very difficult for the adept of the PLO to understand that the term class instance in Russian indicates a class of objects, and not an element of a class consonant with this term — an object of a class. For many who have studied OOP, the terms instance and element are indistinguishable. Let's deal with these terms carefully.

Definitions of Terms

Term instance

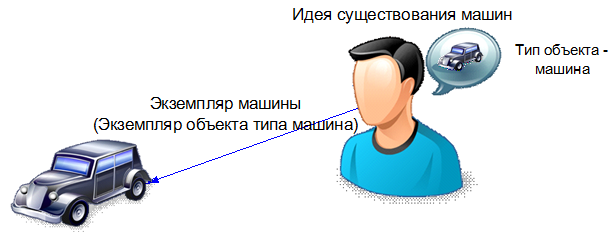
An instance is an object from a number of similar ones. That is, a copy of a machine is an object from a number of similar machines. Aristotle believed that the subject has the idea of ​​the existence of machines. This idea is expressed in the form of an abstract type of objects (machines) that exists in the minds of subjects. When a subject looks at an object, he compares what he sees with the image he has in his imagination (with the type of machines), and if he finds similar features, the object is called a machine, or a copy of the machine. The list of similar features Aristotle called the type. And the object possessing these features is an instance of this type.
')


Following logic, an instance of a class is an object from a number of similar classes. Thus, in Russian, the term instance of a class points us to a class.



A machine belongs to a class of machines like this: a machine is an object of a class of machines.



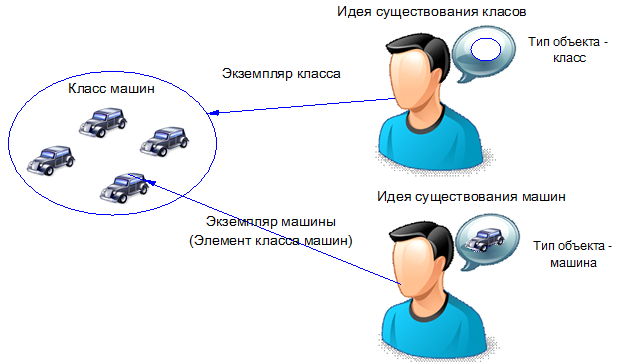
Therefore, if you say, as is customary in the PLO, that a machine is an instance of a class of machines, then it turns out that a machine is a class of machines. Collision!

In OOP, the term class means the term type. Therefore, the term class instance in OOP should be read like this: an instance of the type of objects. Then our picture will look like this:



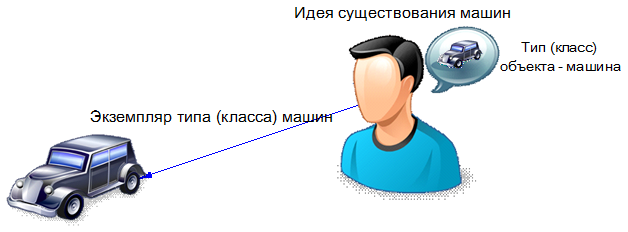
Therefore, if you meet the term class instance, then know that most likely, this term is generated by the PLO, and therefore it is the type of object. Outside the OOP class means a lot of objects.

Term element

The element is part of something. The board element is a resistor, the leg element is a knee, the set element is an object. Thus, the term element may denote a connection between two entities. This connection may be a composition connection (the element of the machine is a wheel)



or communication classification (element of the class of wheels - the wheel).

Other pairs of incorrect terms:

In addition, other incorrect term pairs are now common in business analysis: an event and a copy of this event, a process and a copy of this process, a contract and a copy of this contract. In Russian there is no such thing as an object and an instance of this object. There are terms object type and an instance of this object type.

Perhaps the erroneous use of terms arose due to the incorrect translation of the term instance from the English language. Instance is translated as an example, or as a case, but it is not translated as an instance.

Be that as it may, let's see the proper use of the term instance:

• An instance of an electron is an electron, an instance of a particle of the electron type, or an instance of this type of electrons (but not an instance of this electron).
• A process instance is a process, an instance of a process type object, or an instance of a given process type (but not an instance of this process).
• An event instance is an event, an instance of an object of type event, or an instance of this type of event (but not an instance of this event).
• An instance of a class is a class, an instance of an object of type class, or an instance of a given class type (but not an instance of this class)

These statements are made in the paradigm of Aristotle, where there are object types and instances of these types, but not objects and instances of these objects. I wrote about the paradigm of Aristotle in the article: Introduction to the paradigms of building domain models .

Analogy with science

It should be noted one very interesting fact. It begs the analogy between religion and science. A scientific approach arose to counterbalance the religious description of the world. If you describe the world from the point of view of religion, then you must understand that the presence of God cannot be verified. The basis of faith is faith. A scientific approach, in opposition to faith, places the primacy of the experiment. That is, if the experiment confirms the existence of Paradise, then Paradise exists. If it does not confirm, then it is not known whether it exists or not. The terms used in one concept do not mix with the terms used in another. For example, you can sometimes hear the thesis that someone has proved the existence of God. But as soon as someone proves it, God will cease to be God and will become another concept. Therefore, it is impossible to prove the existence of God, and therefore it is impossible to introduce the term proof in religion. Just as in religion it is inappropriate to talk about evidence, in science it is meaningless to talk about faith, except in terms of: this faith helps me to think, but as soon as it interferes, I will change it.
Similarly, in ontology, there are two approaches: one invented by Aristotle. This is the theory of types. The second was invented in opposition to the Aristotle types. This approach is called the logical paradigm and uses the term class. These two paradigms are immiscible, like science and religion. Therefore, the term class cannot be used in the theory of types, and the term type cannot be used in the theory of classes. However, the PLO violated this prohibition. For this he needs to say fu.

In my presentations, I rely on a logical paradigm in which there is an object and there is a set of objects, called an object class, but there are no terms instance, type and term class in the sense of OOP. To get acquainted with the logical paradigm, I can advise reading the books Chris Partridge Business Objects: Re-Engineering for Re-Use , Matthew West Developing High Quality Data Models .

The basis of the logical paradigm: communication, classification and specialization

Suppose there is a class of objects called wheels. This class contains all the wheels in the world that were, are and will be there. By definition, the fact that an object of this class (a wheel) belongs to a class of wheels is indicated by a link classification.



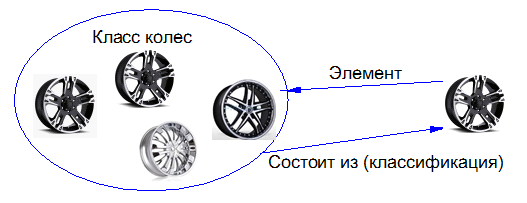
There is no such connection in OOP, and you will not be able to indicate it on the UML diagram.

Let there is a subclass (subset) of this class — the class of wheels being studied (for example, the class of wheels belonging to the same machine). By definition, the fact that this class is a subset of the class of all wheels is indicated by the link specialization.



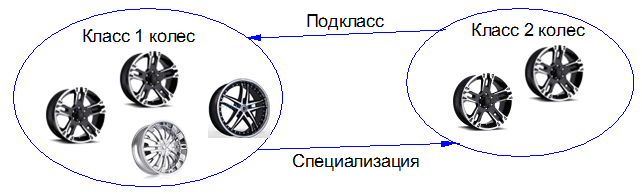
In OOP, such a relationship between classes is called inheritance. It is said that Class 2 is inherited from Class 1.



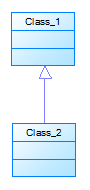
But in nature, Class 2 is a subset of Class 1. Apparently, it means that attributes or parameters are inherited. But the parameters are only in the type description! And again we rest on the confusion of terms. Classes cannot inherit anything. But the types - can.

You can read about specialization and classification here: Information objects or the reason for one misconception (In the paragraph “Decision in a logical paradigm”, I showed how you can model the subject area using these terms).

The division into classes and objects of classes allows me to consider any objects of the class under study, for example, the class of elephants (study the lifespan of any elephant, the length of its tusks at different stages of its life), as well as the class of elephants (study the average duration of elephants, average height and average weight). It is clear that any elephant of a class cannot “know” information about the average duration of life of all elephants. This information is “known” only by the elephant class. Try in the paradigm of Aristotle to come up with the object that “knows” about the average height of elephants, without using the term set! It is unlikely that you will succeed. Therefore, if you are an analyst, you will have to work with objects and classes of objects (but classes are not the sense of OOP).

Let me remind you: a class in the logical paradigm and a class in the PLO are two different things. A class description in a logical paradigm is an enumeration of objects of this class, and not properties of these objects. In OOP, a class description is understood as a description of the properties of objects, which, in fact, means a description of the type of objects. Those who teach OOP do not hide the fact that a class in OOP is a type of object. But why the type was called a class, do not disclose.

Example
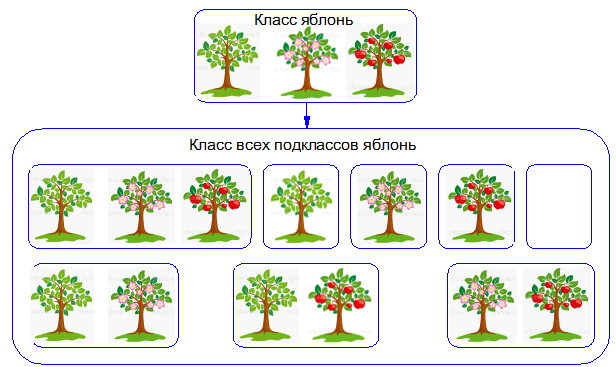
To understand why the definition of a class in OOP does not work in the real world, try performing the simplest operation on a class: create a class of all subclasses of this class. And try to apply a class definition to each subclass you create that acts in OOP.

Example: Let us have three apple trees {1; 2; 3}. This is a class. OOP requires that features of this class have common features. Let it be a sign of "the presence of apples." Let's create a class consisting of all subclasses of the class of these apple trees. This class consists of the classes: {{empty}; {1}; {2}; {3}; {1; 2}; {1; 3}; {2; 3}; {1; 2; 3}}.



That is, in this class of classes there are 8 elements. Try, if you follow the definition of the class of OOP, to give a differentiated description of these classes (the other is meaningless). And these flowers - only three elements in the class. And if there are 1000, and if there are countable set, and if there is a continuum? Therefore, in the OOP there is not even the simplest operations on classes (addition and subtraction of sets).