Building crosswords using the Wolfram Language (Mathematica)

Translation of Michael Trott's post, “ Constructing Crossword Arrays Faster ”.
Download the translation in the form of a Mathematica document that contains all the code used in the article here .

In chapter 6 of my book Mathematica GuideBook for Programming , as an example of working with lists, I discussed how to build an array that represents a crossword puzzle. Although this example was good for demonstrating advanced work with lists, however, the use of lists is not the best way to build an array of crossword puzzles. The complexity of adding a new word to an array with n - 1 words already placed was for this algorithm Thus, the total difficulty of creating an array of crossword of n words became equal to .

Over the past few years, some Mathematica users have asked me if a faster algorithm can be built. The answer is yes, you can. If we use hashing methods, we can quickly and at the same time check whether it is possible to use some element of the array and, therefore, we can reduce the overall complexity of the algorithm with before that for crosswords of thousands of words will give a big difference in time spent on calculations. This algorithm is implemented in this article. When we place individual letters of a word in a certain rectangular table, many different situations need to be considered. As a result, the article contains more than usual amount of procedural code. Although some definitions of functions are somewhat long, thanks to the comments between the steps of the calculations and the decision branches, the code should be fairly simple to read and understand.

In order for the article to be self-sufficient, we will not use any algorithms implemented in the GuideBook .
')
Here is the statement of the problem that we will solve:

Suppose we are given a list of words as strings. Our task is to insert them into a rectangular table consisting of squares so that each word is placed horizontally (read from left to right) or vertically (read from top to bottom), and the words must be connected in squares containing the same for them letters.

Here is an example that uses the names of scientists (citizens of the USSR and Russia) who have become Nobel laureates. (In the rest of the article, we will use words that are directly related to Mathematica as examples.)



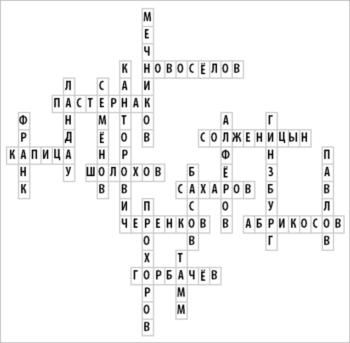
To improve the readability of the crossword, we also require that any two horizontal or any two vertical words be separated from each other by at least one empty square. In addition to this, no horizontal word should begin or end in a square that is adjacent to a square occupied by a letter of a vertical word, and, similarly, no vertical word should begin or end in a square that is adjacent to a square occupied by a letter of a horizontal word . (In other words, the squares adjacent to the left and right of the horizontal word and the squares adjacent the top and bottom of the vertical word must remain empty.) However, we allow words to begin or end in squares occupied by another word.

We will place all the words in a square table (not limited in size), built from separate squares and we will track the contents of each square.

Function

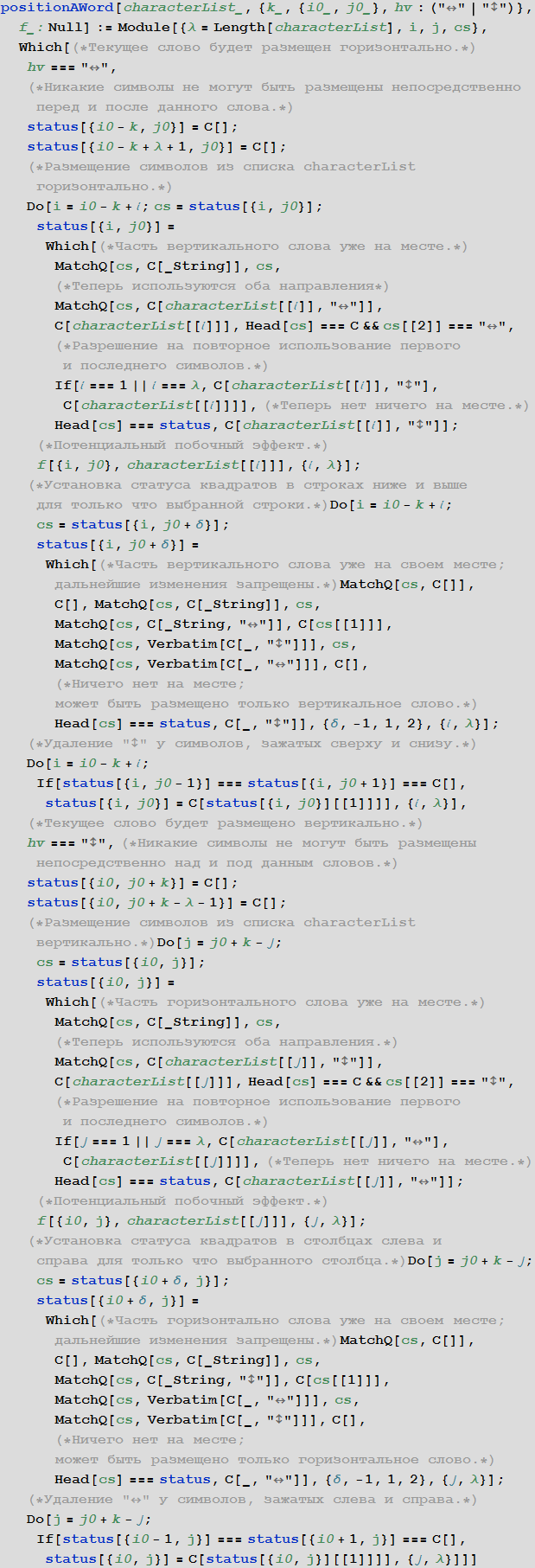
positionAWord [characterList, k, {i0, j0}, hv]

arranges the characterList character list in such a way that the kth element of the list will be located in the square { i0 , j0 } and the word characterList will be located according to the value of the parameter h v (horizontally or vertically, which will be marked with "" or "", respectively) . We will use the construction of the form C [data] to set the current status of the square, while the following situations are possible:

• C [] - the square must remain empty;
• C ["char"] - a square contains the symbol char and is part of a horizontal or vertical word.
• C ["char", ""] - a square contains the char character in a vertical word and can also be used in a horizontal word.
• C ["char", ""] - a square contains the character char in a horizontal word and can also be used in a vertical word.
• C [_, ""] - the square does not yet contain any characters and can be used in the horizontal word.
• C [_, ""] - the square does not yet contain any characters and can be used in a vertical word.

All this information will be associated with status values ​​down values. At the same time, status [{i, j}] will calculate the current state of the square centered at the point {i, j}. At the output, it will produce an object of the form C [...] or remain in a non-computed form, if the square has not yet been used in any way or is not a neighbor for some of the words already in the table.

We associate the value of this function with the current content of the square by means of the expression status [square] = value . This will allow us to fix the search time for the status of each of the necessary squares by calculating the expression status [square] .

The positionAWord function sets the values ​​of the squares in which the characters of the word are placed, and also adds information about the potential use of adjacent squares in the future. For example, squares located directly above or below a horizontal word can only be used for vertical words in the future.

The optional last argument of the positionAWord function is used to create possible side effects, such as, say, monitoring the order of adding words, which we will use below. In the implementation of this function, we had to consider a large number of different situations - this is easily seen in the comments to the code below.

In [1]: =



As an example, we place the word Mathematica , starting from the square {1,1} horizontally.

In [2]: =



Below is a list of the squares that have been marked.

In [3]: =



Out [3] =



In order to see the build process live, let's create a function makeCWPGridGraphics , which will color the squares according to their current status.

In [4]: ​​=



The graph below shows the current status of the squares adjacent to the symbols already arranged in squares.

In [5]: =



Out [5] =



Function

positioningAWordIsPossibleQ [characterList, k, {i0, j0}, hv]

checks whether the list of characters characterList can be arranged in such a way that the kth element of the list is located in the square {i0, j0}, and the word characterList is located according to the value of the hv parameter (horizontally "" or vertically ""). In order to do this, we need to check that each of the required squares is either available or has the required symbol already in place. Also, adjacent squares must either be empty or must have letters from a word that is already perpendicular. The auxiliary function whileTrueLoops is an iterative function that finishes its work as soon as the first incompatible square is found using the Throw - Catch technique. In the future, we will always assume that a new word is placed only with the help of the positionAWord function and only when the positioningAWordIsPossibleQ function returns the value True.

In [6]: =



In [8]: =



If we have already placed the word Mathematica horizontally, we can arrange another copy of the word Mathematica vertically.

In [9]: =



Out [9] =



But we cannot horizontally place the word Mathematica in the same position.

In [10]: =



Out [10] =



In general, it would be possible to place another copy along the one already located, starting with the letter “t” in the position {3, 3}.

In [11]: =



Out [11] =



Of course, we could put another copy of the word Mathematica in the middle, say, make it vertical, passing through the second letter “m” of the horizontal copy of the word Mathematica .

In [12]: =



Out [12] =



In [13]: =



Using the code below, we can visually display the current state of our table.

In [14]: =



Out [14] =



Function

findAPossiblePositionAndPositionAWord [characterList]

looks for a possible location of the characters characterList and then places them. The function returns either the coordinates of the added character, or $ Failed, in case there is no way to add the word. We also provided this function with several fairly obvious options that, among other things, allow us to place words as tightly as possible, or vice versa, as freely as possible. If the value of the AttachmentPosition option is made equal to Inner , then the function tends to add each new word inside the already placed ones, Outer value - on the contrary, if the RandomSample value is used , then the position of the new word is chosen randomly.

In [15]: =



In [16]: =



In [17]: =



Finally, we will create the function makeCWPGrid [status] , which will construct, in fact, a table of letters based on the down values ​​of the status function.

In [18]: =



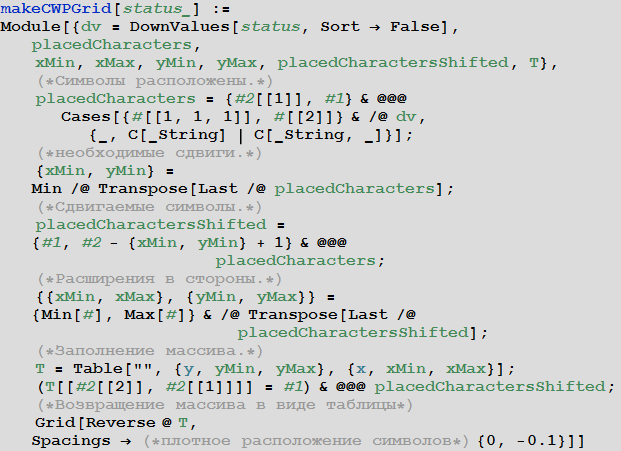
The graph below shows the state of all the already added squares after the word Mathematica was added 6 times to the original. Gray squares correspond to words already placed; red - must remain empty; green - new words can be added through them. Arrows indicate in which direction you can add new words.

In [19]: =



Out [22] =



In [23]: =



The graph below shows some of the steps involved in building an array of crossword puzzles. If you carefully study the device of squares in each of the figures (for each of the options), it becomes much more understandable how the algorithms presented above are arranged.

In [25]: =



Out [25] =



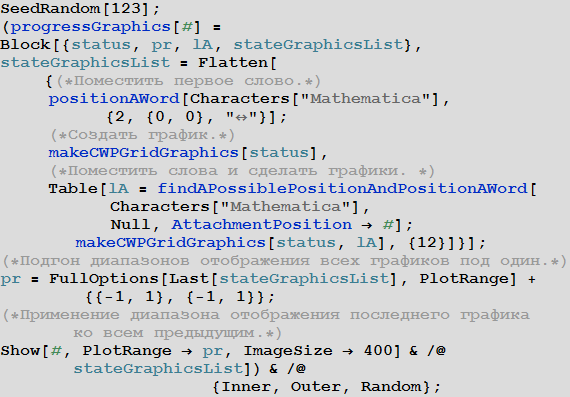
Using the Manipulate function, we can easily create an interactive version of the algorithm that will allow us to follow its steps clearly and simply. The following interactive version of the algorithm allows you to follow its 12 first steps for different values ​​of options.

In [26]: =



Out [26] =



Now let's consider the complexity of the implemented method. Due to the fact that the search for the current state of a square is almost constant (independent of the number of squares already specified), we expect the linear complexity of O ( n ) depending on the number of words. As a test, we will find the placement of the 500 words Mathematica . To visualize the calculation process, we will use the Monitor function.

In [27]: =



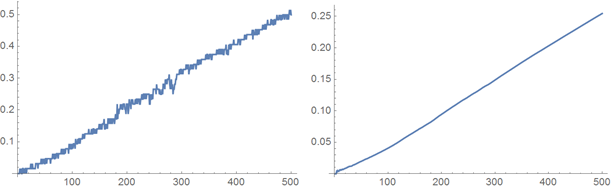
Now we will draw the measured values ​​of the elapsed time. The graph on the right shows the average time to add a specified number of words. It grows linearly with the number of words you need to add.

In [30]: =



Out [30] =



Thus, the total time of forming an array of n wordword crossword is of order complexity . The graph shown below clearly demonstrates this (black - elapsed time, red - found model of the form ).

In [31]: =



Out [32] =



Below is the resulting crossword array. We use a small font size to display it here in full.

In [33]: =



Out [33] =



Due to the much higher speed of this approach, based on hashing for a large number of words (say, thousands), we can now very quickly create a crossword puzzle, say, of 250 words. In this case, as a list of these words, we take 250 selected randomly embedded functions of the Wolfram Language ( Mathematica system).

In [34]: =



Out [38] =



In [39]: =



Out [39] =



The graph shown below displays the order in which the words were located on a plane (in the table). Red, high columns correspond to words that were added at the beginning, blue, low “turrets” - added later.

In [40]: =



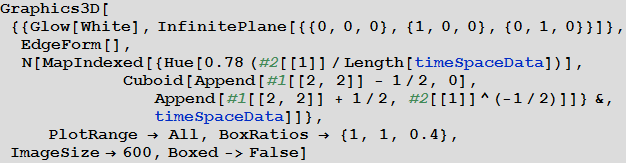
Out [40] =



Now we will build an array of crossword, consisting of the names of the functions (and their options) associated with various visualizations in the Wolfram Language.

In [41]: =



Out [42] =



In [43]: =



In [47]: =



Out [47] =



Now create a potential function f for the position function AWord . This function will be used to determine which particular word already belongs to one or another character.

In [48]: =



Now let's create some variation of the function makeCWPGrid , which will use the information associated with the function f to color the words.

In [53]: =



The result is presented in the table below. The color of the letters standing at the intersection of words is mixed.

In [54]: =



Out [54] =



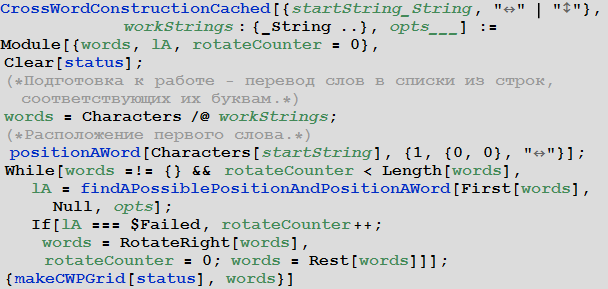
We will finish the article by creating a single function CrossWordConstructionCached , which serves to create a crossword puzzle based on the list of words that is given to it at the entrance.

In [55]: =



The constructed algorithm can work with any characters. As an example, there are two ways to make a crossword puzzle from all three-digit prime numbers.

In [56]: =



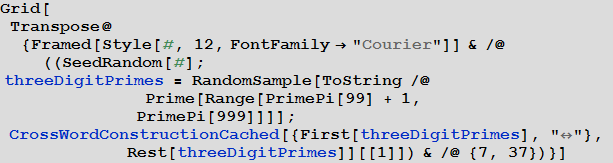
Out [56] =



Or you can create a crossword puzzle of the names of all the Nobel laureates (citizens of Russia and the USSR):

In [57]: =



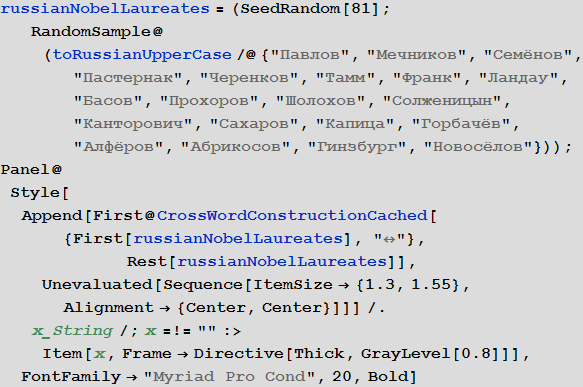
Out [58] =



Resources for learning Wolfram Language (Mathematica) in Russian: habrahabr.ru/post/244451