Curves Beziers de Castelgio. HTML5 Canvas

Foreword

In my free time I decided to do an interesting job. I got the idea to write a small framework for canvas (although a bicycle, but also interesting). It came to Bezier curves.

I decided to somehow embellish the built-in solution, but it has one drawback. The problem is that the quadratic and cubic curve functions produce a ready-made result that cannot be edited. I needed to draw the curve gradually or to draw only a part of the curve, not to mention the fact that I wanted to draw curves of a greater order than 2-3 degrees.

Began to google. Found an interesting article on Habré. But my knowledge of mathematics did not allow me to convert it to my needs, and besides, timers are used there, because of which it is impossible to stop the animation in time.
')
I start writing from scratch.

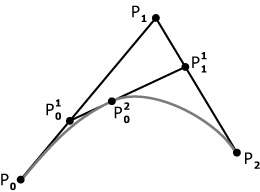
Everything was not so scary. The essence of the de Costelgio algorithm itself is simple, so why use such a tricky formula? So I will not.

Briefly tell the algorithm, and then a sample code.

A function that calculates a curve returns only a point by offset (that is, by the distance from the beginning of the curve in percent). Gradually increasing the offset we get more and more new points. When you want, you can stop the algorithm, beauty! And do not need a bunch of timers, just one setInteval which will gradually query and draw points.

The getPointOnCurve function recursively calculates segments from the points passed to it.
Having calculated, by the offset, it finds new points on these segments, which it passes on to itself. Continuing until a point on the curve is found, which it returns.

//      formula formula.getPointOnCurve = function(shift,points){ if(points.length == 2){ return this.getPointOnLine(shift,points); } var pointsPP = []; for(var i = 1;i < points.length;i++){ // getPointOnLine    ,  .    pointsPP.push(this.getPointOnLine(shift,[ points[i - 1], points[i] ])); } return this.getPointOnCurve(shift,pointsPP); }; 

Helper function getPointOnLine:

 formula.getPointOnLine = function(shift,points){ //,   points   : [[x0,y0],[x1,y1]] return [ (points[1][0] - points[0][0]) * (shift / 100) + points[0][0], (points[1][1] - points[0][1]) * (shift / 100) + points[0][1] ]; }; 

And here is the drawing itself:

 //     var points = [ [10,50], [40,-40], [190,180], [40,-60], [80,130], [10,50] ];//   var shift = 0; var step = 1;// shift     step var timer = setInterval(function(){ context.beginPath(); context.moveTo(points[0][0],points[0][1]); if(shift > 101){ shift = 101; } for(var i = 0;i <= shift;i += step){ var coord = formula.getPointOnCurve(i,points); context.lineTo(coord[0],coord[1]); } context.closePath(); if(shift <= 100){ shift += step; } },fps) 

And, of course, an example .

I hope someone helped, because he himself for a long time could not figure it out.