Content of the main course

• Article 1: Bresenham algorithm
• Article 2: rasterization of the triangle + clipping of the rear faces
• Article 3: Removing invisible surfaces: z-buffer
• Article 4: Required Geometry: Matrix Festival
  
  • 4a: Construction of perspective distortion
  • 4b: we move the camera and what follows from this
  • 4c: a new rasterizer and perspective distortion correction
• Article 5: We write shaders for our library
• Article 6: A little more than just a shader: shadow rendering

• Article 3.1: It’s time to refactor
• Article 3.14: Beautiful Matrix Class
• how does the new rasterizer work

Communication outside Habr

If you have questions and do not want to ask them in the comments, or simply do not have the opportunity to write in the comments, join the jabber conference 3d@conference.sudouser.ru

4 Welcome and introduction

The numbering in the last article ended with 3, in this we will continue to number through.
UPD: ATTENTION! The section, starting with numbers 3.1, 3.14 and 3.141 and on, will be about the intricacies of the implementation of the basis of the basics of computer graphics - linear algebra and computational geometry. About the principles of graphics writes haqreu , but I will write about how it can be clearly programmed!

This article is a continuation of a series of articles on the practical implementation of elements of computational geometry, and, in particular, software renderers, using C ++ 98. We haqreu deliberately go to using the previous version of the standard and writing our own geometric library in order to, first, release the code of examples, which without special difficulties will be compiled by most of the available compilers, and second, that there is nothing in our code that is hidden in the bowels of the library. The article outlines the implementation of a rectangular matrix pattern: template<size_t DimRows,size_t DimCols,typename number_t> class mat;
')

4.1 Acknowledgments

I express great appreciation to haqreu as the founder of this course. Keep it up!
I am very grateful to lemelisk for the preliminary review and review of my sources. Thank you for the fruitful discussions!
I also have to thank Mingun for the valuable comment on the design of the templates. I hope they have become more readable.

4.2 A little philosophical remark about language, mathematics, C ++, and all such

In general, abstractions such as “matrix” and “vector” and operations on them are necessary in order to simplify and formalize the language of presentation of geometry. Without them, we would have to constantly say (and write in the program) something like:

We speak:

To get the new coordinates of Point, which is moved in the direction of Direction, you need to add
x point of point with x moving direction,
Point Point with y Direction moving,
z Point Point with z Direction Moving

We write:

 Point.x=Point.x+Direction.x; Point.y=Point.y+Direction.y; Point.z=Point.x+Direction.z; //(, "  ") 

After the concept of "vector" entered our speech, we can already say:

To get the new radius vector of Point after moving in the direction of Direction, you need to add the Point and Direction vectors

And after including the vec template in our code, we can write:

 Point=Point+Direction; 

Thus, we shorten what we have written, we insure against mistakes when copying, pasting and editing, and we get a way to reason with more succinct terms.

Here is what Jeff Alger writes about this in the book “C ++ for Real programmers”, (by AP Professional, translation published by Peter, entitled “C ++: Programmer’s Library”)

C ++ is actually not so much a language as a tool for creating your own languages. Its elegance lies not in simplicity (C ++ words and simplicity cut the ear with their apparent contradiction), but in its potential. Behind every ugly problem hides some clever idiom, an elegant language trick, thanks to which the problem melts right in front of our eyes. The problem is solved as elegantly as a real language like Smalltalk or Lisp would have done, but your processor is not smoked by voltage, and stocks of manufacturers of memory chips do not grow on Wall Street

This is exactly what we are going to do - we will build a geometric primitive control language using C ++, trying to do this as close as possible to the definitions from mathematics.

5 Template class for processing and storage of matrices

We store the matrix as an array of row vectors using the appropriate specialization of the vec template. Our template is focused only on working with matrices of small dimension (maximum 10x10 elements. Although it will be terrible already). But in computational geometry, as a rule, all work goes precisely with matrices no more than 4x4. Large matrices, as a rule, are very sparse — for them it is known in advance that they are almost completely filled with zeros, which makes it possible to optimize their processing and storage.

5.1 Index Operators

We defined the constant and non-constant variants of the index operator [] so that they return a reference to the corresponding vector row of the matrix:
Two variants of operators are needed because we, wherever possible, use const . If there were no constant variant of the index operator, the compiler would not allow us to compile code in which, for example, the operator is called by a constant reference to an instance of the matrix:
In addition, we use the assert() macro here to catch attempts to refer to a nonexistent row of the matrix. Read more about assert in article 3.1.

5.2 Calculation of the inverse matrix

We needed a subroutine to calculate the inverse matrix. In particular, using the inverse matrix, one can “beautifully” find the barycentric coordinates (you can see in my branch on the githabe , the filltria function).
The task of calculating the inverse matrix in the general case is quite time consuming and can be accompanied by the accumulation of significant errors in the calculations. However, for such small matrices, these problems are not so significant (if you do not specifically build such an example). We chose an algorithm using the allied matrix, because it seemed to us more transparent than the Gauss-Jordan algorithm. The following fact is used:

• if for a given matrix to make an ally matrix,
• and then transpose
• and divide it by the determinant of this,

we get the inverse of the matrix. These are just three distinct steps.
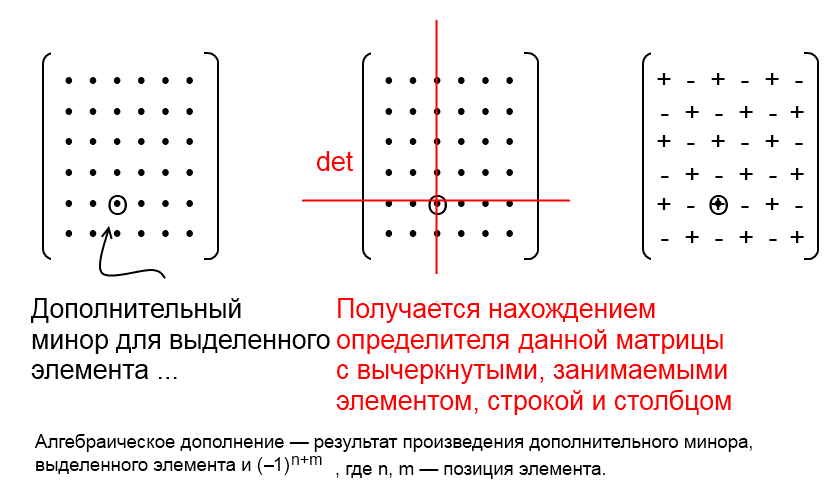
The union matrix is ​​composed of algebraic additions. An algebraic addition is the determinant of the submatrix obtained from the principal by deleting the row and column containing the element for which we find this addition.

Got the next question - how to find the determinant.
We use the following property:

the determinant is equal to the product of the elements of the row or column of the matrix by their algebraic complements.

A recursion is obtained - the algebraic complement is also the determinant of the matrix, only the dimension is one less. And the determinant of a matrix of dimension 1 is its only element. Recursion is closed. We will use the beautiful feature of C ++ templates — we will deploy this recursion right at compile time.

Note: Our matrix is ​​rectangular, and the determinant can be calculated only for a square matrix. At the compilation stage, I would like to catch attempts to find the determinant of a non-square matrix. There are two ways to do this:

• inherit from mat the squareMat class in which to declare the determinant
• use the fact that the dimensions of the matrix are known to us at the compilation stage, so we can compare them and interrupt the compilation, if they do not match

In the first case, we get a separate type of matrices and a bunch of problems with matrix transformation back and forth, because we can form a square matrix within the mat type, but to calculate the determinant, we have to construct an instance of the squareMat type from it.
Therefore, we will choose the second method - when expanding templates, detect a size mismatch and break the compilation. In C ++ 11 there is a standard tool to do this - static_assert (). In C ++ 98 there is no such means, so we will invent a surrogate:

 template<bool> struct static_assertion; template<> struct static_assertion<true> {}; 

If you substitute true into this template, it simply forms an empty static_assertion {} structure. But if you set it to false, an error is generated (an attempt to use an incomplete declaration of the static_assertion structure), which stops the compilation:

 geometry.h:125: : invalid use of incomplete type 'struct static_assertion<false>' static_assertion<DimCols<=10>(); ^ 

The more errors shifted to the compilation stage, the better, because they simply do not allow bad code to work.
Let's return to our recursion:

So, for all situations when the first parameter of the template is not equal to 1, the upper template (lines 1-11) will be used. For the situation, the first parameter is 1 , a special version of the template is defined (lines 12-18). Pay attention to line 13: Addition <1,number_t> just also indicates that this announcement is a separate entity. With a common version of the dt template, nothing binds it. There is an error when confusing the behavior of partial specialization and inheritance, expecting that everything declared in the general version will be in partial. This will not happen - the programmer is charged with recreating, in a partial specialization, all that he needs.

• The wrapping into a separate structure is performed because the standard does not allow partial specialization for functions.
• We removed this function from mat because, having acted differently, we would be forced to add in mat <1,1, number_t> part of the methods from the general version, which would lead to some swelling of the code.

Partial specialization, exactly by definition of the 1x1 matrix determinant, gives us a single element (line 16).

The common version of the template performs the decomposition of the matrix on the zero line - it takes an element with the index 0, i from the first line, multiplies it by the algebraic complement - cofactor(0,i) and the result accumulates in the variable ret . Everything is in complete agreement with the formula of this decomposition:

5.3 How recursion happens

IMPORTANT: Strictly speaking, the template processing mechanism is the compiler's own business. Below, I talk about how this could happen . This is done only to illustrate how template declarations unfold recursively.

Imagine that we independently deploy templates. Code written:

 ... using namespace std; int main() { mat<3,3,int> m; .... cout << m.det() << endl; return 0; } 

We see in it a call to det () from the mat template, which means we should get the text of the det () function for the specific case of mat <3.3, int>.

Template	The result of the substitution DimCols = 3; DimRows = 3; number_t = int
number_t det() const { static_assertion<DimCols==DimRows>(); return dt<DimCols,number_t>::det(*this); }	int det() const<3,int> { static_assertion<3==3>(); return dt<3,int>::det(*this); }

Great, now we need from the template <size_t Dim, typename number_t> struct dt to get the specific text for the case dt <3, int>:

Template	The result of the substitution is Dim = 3; number_t = int
template<size_t Dim,typename number_t> struct dt { static number_t det(const mat<Dim,Dim,number_t>& src) { number_t ret=0; for (size_t i=Dim; i--;) { ret += src[0][i] * src.cofactor(0,i); } return ret; } };	struct dt<3,int> { static int det(const mat<3,3,int>& src) { int ret=0; for (size_t i=3; i--;) { ret += src[0][i] * src.cofactor(0,i); } return ret; } };

We met the call to the operator [] and cofactor () from mat <3.3, int>. The body [] is of no interest to us now, we are investigating with cofactor ():

Template	The result of the substitution DimCols = 3; DimRows = 3; number_t = int
number_t cofactor(size_t row, size_t col) const { return get_minor(row,col).det()*((row+col)%2 ? -1 : 1); }	int cofactor(size_t row, size_t col) const { return get_minor(row,col).det() *( (row + col) % 2 ? -1 : 1); }

Here, get_minor () is called. Get the text for it:

Template	The result of the substitution DimCols = 3; DimRows = 3; number_t = int
mat<DimRows-1,DimCols-1,number_t> get_minor(size_t row, size_t col) const { mat<DimRows-1,DimCols-1,number_t> ret; for (size_t i=DimRows-1; i--; ) { for (size_t j=DimCols-1;j--;) { ret[i][j]=rows[ i<row ? i : i+1 ] [ j <col ? j : j+1 ]; // j <col ? j : j+1 col // i<row ? i : i+1 - row } } return ret; }	mat<2,2,int> get_minor(size_t row, size_t col) const { mat<2,2,int> ret; for (size_t i=2; i--; ) { for (size_t j=2;j--;) { ret[i][j]=rows[ i<row?i:i+1 ] [ j<col?j:j+1 ]; } } return ret; }

We got this get_minor () to return a 2x2 matrix already. Now we, for the 2x2 matrix, will call mat <2.2, int> :: det (). But we only have the body mat <3.3, int> :: det (). Therefore, we dive into recursion by one step and build another set of methods:

Having expanded the pattern chain, we again encountered the call to get_minor () in the body of cofactor (), but for the case of DimCols = 2, DimRows = 2. The resulting version of get_minor () returns a 1x1 matrix. Further, for it in the body of cofactor () a determinant is requested. Again we should get the text mat :: det (), but for the case DimCols = 1; DimRows = 1.

Template	The result of the substitution DimCols = 1; DimRows = 1; number_t = int
number_t det() const { static_assertion<DimCols==DimRows>(); return dt<DimCols,number_t>::det(*this); }	int det() const<1,int> { static_assertion<1==1>(); return dt<1,int>::det(*this); }

Great, now we need from the template <size_t Dim, typename number_t> struct dt to get the specific text for the case of dt <1, int>. STOP , this also falls under the partial specialization of the template dt <1, number_t>! It is necessary to process it, and not the general version of the template!

Template	The result of the substitution is Dim = 1; number_t = int
template<typename number_t> struct dt<1,number_t> { static int det(const mat<1,1,number_t>& src) { return src[0][0]; } };	template<typename number_t> struct dt<1,int> { static number_t det(const mat<1,1,int>& src) { return src[0][0]; } };

We see that there is no longer access to cofactor (). At this, the recursion promotion is over - we got the bodies of functions for calculating the determinant of 3x3, 2x2, 1x1 matrices.
Important note: You may wish to write this:

 number_t det() { if(DimCols==1 && DimRows==1) { return rows[0][0]; } number_t ret=0; for (size_t i=DimCols; i--;) { ret += src[0][i] * src.cofactor(0,i); } return ret; } 

The motivation is simple - it will be sort of like ordinary recursion, and partial specialization is not needed. However, during the deployment of templates, the compiler will not do anything with the conditional operator, but will start building templates (3, 2, 1, 0, std :: numeric_limits <size_t> :: max, std :: numeric_limits <size_t> :: max- 1, ...) until it is stopped by the internal counter -ftemplate-depth= (by default, this depth is 900).
The ability to use familiar flow control operators appears in C ++ 11 for functions declared with the constexpr . They allow you to organize another type of computation at compile time , different from recursion on templates. And if I can not turn all of our render during compilation?

So, we have described in terms of C ++ the search for the determinant of a matrix, as well as the operations accompanying it - the construction of a minor matrix and an algebraic complement. To find the inverse matrix, it remains only to construct an allied matrix:
acts exactly by definition - fills the matrix with algebraic complements of the corresponding elements.
It remains to perform the main stage of construction - to find the inverse matrix (it will be obtained in transposed form):

 mat<DimRows,DimCols,number_t> invert_transpose() { mat<DimRows,DimCols,number_t> ret = adjugate(); //   number_t det = ret[0]*rows[0]; //   ,   //  - //       return ret/det; //     , //      } 

5.4 Matrix Multiplication

The operation of matrix multiplication is also quite time consuming and may be accompanied by an accumulation of error. In cases of matrices of higher dimensionality (greater than 64x64), special algorithms, like the Strassen algorithm , are usually used. The asymptotic record holder, the Coppersmith-Winograd Algorithm (with Virginia Williams improvements), is not used now, because it starts to overtake the Strassen algorithm on matrices so huge that they are not yet encountered in modern computational practice. We have small matrices, so for the multiplication we are simply satisfied with the definition of the matrix multiplication operation:

The product of matrices AB consists of all possible combinations of scalar products of the row vector of matrix A and the column vector of matrix B

The definition in this form allows us to use the scalar multiplication operation from our vec template. But for this we need a method that extracts its column from the matrix as a vector:
Yes, there seems to be too much copying (later we will see if the compiler can cope with throwing it out), but the main goal is to write such a short and capacious multiplication of matrices:

 template<size_t R1,size_t C1,size_t C2,typename number_t> mat<R1,C2,number_t> operator*( const mat<R1,C1,number_t>& lhs, const mat<C1,C2,number_t>& rhs ) { mat<R1,C2,number_t> result; for (size_t i=R1; i--; ) { for (size_t j=C2; j--;) { result[i][j]=lhs[i]*rhs.col(j); //  i-    //  j-   } } return result; } 

Pay attention to this text. Here, C ++ sets out the mathematical definition of the multiplication operation of rectangular matrices, and this is done very close to the text [“filling the result matrix with all possible scalar products of the row vector of the left matrix and the right column vector”].
At the same time, the control of dimensions (the number of columns of the left should be equal to the number of rows of the right) is performed immediately at the compilation stage - an attempt to multiply matrices that are not suitable for the size does not even compile.
And this is very important, because the runtime error can be floating, elusive, and so on. And the compilation error gets out almost always. (It is necessary to take into account the madness of the IDE, which can part of the project to cache, part to forget to update, and so on. But there is a sure cure for this - Rebuild All).

5.5 Single Matrix Generator

In his text:

 static mat<DimRows,DimCols,number_t> identity() { mat<DimRows,DimCols,number_t> ret; for (size_t i=DimRows; i--; ) { for (size_t j=DimCols;j--;) { ret[i][j]=(i==j) ; } } return ret; } 

There is an interesting feature - writing the result of type bool into a variable of a priori unknown type number_t. Here a nightmare can happen to a person who would like to use our geometry in his project, and together with a self-made type for storing numbers (this may be a type that stores numbers with a fixed comma). He may not expect our methods to try to write bool values ​​to his type (operator == for size_t returns bool), and pile up his own constructor that accepts bool and does not convert this conversion as described in the standard ([§4.7 / 4 ] requires that when casting bool to a numeric type, false becomes 0, true to 1). Since in this case, a hypothetical user deviates from the standard, we should not try to lay straw on it (we could do this:ret[i][j]=static_cast<number_t>(static_cast<int>(i==j)) and to transfer at least int to it at the price of a succession of transformations - has violated the standard - it is my fault.

5.6 Matrix multiplication by vector

To multiply the matrix (left) by the vector (right), we consider the vector as a matrix of one column. Further, we can perform the matrix multiplication operation already known to us, which in the end will also give a matrix of one column — this column vector will be the result of multiplication.


Now we can write the matrix-vector multiplication operator:

 template<size_t DimRows,size_t DimCols,typename number_t> vec<DimRows,number_t> operator*( const mat<DimRows,DimCols,number_t>& lhs, const vec<DimCols,number_t>& rhs ) { return (lhs * mat<DimCols,1,number_t>::make_from_vec_col(rhs) ).col(0); } 

It was worked out exactly by definition - they obtained a matrix with one column from a vector, multiplied it, returned a column-result.

5.7 Dividing the matrix by a scalar, output to ostream

Performed using the fact that the matrix is ​​stored as an array of vector - rows, and for the vector similar operations have already been written:

6 Conclusion

In this article, I tried to describe as much as possible the construction of the mat class template. In the next article I will discuss the issues of optimization and acceleration of this code on x86_64 and ARM architectures (using the example of STM32F3). See you soon article!