C ++ 11 variadic templates and long arithmetic at compile time
In the thirty years that have elapsed since its appearance in the depths of Bell Labs, C ++ has come a long way, going from “advanced C” to one of the most popular and expressive compiled languages. Especially a lot, to the author’s purely personal view, gave C ++ a new standard C ++ 11, which is rapidly gaining support for compilers. In this article we will try to “touch with hands” one of its most powerful features - templates with a variable number of arguments ( variadic templates ).
Developers familiar with the Alexandrescu books probably remember the concept of the type list . In the good old C ++ 03, if you need to use a previously unknown number of template arguments, you are asked to create such a list and then use it with a clever hack. This way tuples were implemented (now std :: tuple) and so on. and so on And the chapter on type lists made it clear that on C ++ templates you can perform almost any calculations (do λ-calculus , for example), so long as they can be written in a functional style. The same concept could be applied to long arithmetic: store long numbers as lists of ints, enter the main class of the form
So the foundation is the new syntax introduced in C ++ 11. To begin with, let's look at how the definition of a tuple class, which is not a crime against humanity, should look like:
')
The first way: as a set of argument types of functions or methods. This is done like this:
Well, then what? What can you do with all these arguments?
First, you can simply use further, as the types of other functions or templates with a variable number of arguments:
Secondly, it can be used in more complex transformations. In fact, the parameter pack expansion supports more than just the substitution of everything and everything, separated by commas. So, you can easily implement the following function:
And finally, thirdly (and in the most banal), argument lists can be used in recursion:
With the help of a certain amount of patterned magic, one can learn how to extract from packs the type and value by number and perform other machinations. An example under the spoiler.
We begin our implementation of long arithmetic. First, let's define the main class:
In the best traditions of computation at the stage of compilation in C ++, all, in fact, the data are not stored here, but are the direct arguments of the template. C ++ will distinguish the implementation of the BigUnsigned class with different sets of parameters, due to which we will be able to implement our calculations. We agree that the first parameter will contain the lower 32 bits of our long number, and the last one will contain the most significant 32 bits, including, possibly, leading zeros (personally, I see this as the most logical solution).
Before we deal with the implementation of addition, let's define the concatenation operation on our long numbers. Using the example of this operation, we will introduce the standard tactics that we will use in the future.
So, we define an operation on two types:
It is equally trivial to implement bit operations, for example, (very naive) xor:
Now, actually, addition. Do not go anywhere - you have to use recursion. Define the main class and recursion base:
Now - the main calculations:
So what happened.
View template
Next, the string
Finally, the final calculation finds the result, applying recursion by the rule
Well, you can test! The calculations themselves will look something like this:
Compiled! It started! But ... how do you know the value of C? How, actually, to test?
Easy way: let's call an error at compile time. For example, we write in main
When trying to compile such code, we get a logical error:
A less simple way: let's write a function that will generate a string with a binary representation of a given number. The stock will look something like this:
The new version of our primitive test will look like
The difficult, but most convincing way - the derivation of a decimal representation - will require some work from us, namely the implementation of the division operation.
For this we need certain, uh, prerequisites.
So division. Let's start as expected: with the definition of classes and the task of the base of recursion.
Here we have introduced an additional dummy class
the only function of which is to slightly brighten up the unattractive life of a programmer,
trying to debug a template program. So, when trying to compile a program like
So, the division algorithm itself will be the simplest (and probably rather inefficient). Let it be necessary to divide A by B. If A is less than B, then the solution is obvious: the remainder is A, the quotient is 0. (Actually, the obvious division also produces the auxiliary class
Iiii finally decimal representation! It is clear that to print a decimal representation of a number, you can divide it for a long time by 10. The remainder of the first division will give the youngest character, the remainder of the division of the first quotient by 10 will give the second character and so on. However, we take into account that in C ++ we are not obliged to print number digit by digit; we are quite satisfied to divide the number with the remainder, for example, by 100, in order to get two signs at once. Therefore, we will divide by the largest number that enters
And finally, our code
gives out
-, , .
: (), ,
. ,
.
-, . , , .
( , , , ,
.) , .
-, , —
. — , .
Developers familiar with the Alexandrescu books probably remember the concept of the type list . In the good old C ++ 03, if you need to use a previously unknown number of template arguments, you are asked to create such a list and then use it with a clever hack. This way tuples were implemented (now std :: tuple) and so on. and so on And the chapter on type lists made it clear that on C ++ templates you can perform almost any calculations (do λ-calculus , for example), so long as they can be written in a functional style. The same concept could be applied to long arithmetic: store long numbers as lists of ints, enter the main class of the form
template<int digit, class Tail> struct BigInteger { }; Parameter packs
So the foundation is the new syntax introduced in C ++ 11. To begin with, let's look at how the definition of a tuple class, which is not a crime against humanity, should look like:
template<typename... Types> class tuple { // ... }; Note the three dots in the template arguments. Now Types is not a type name, but a parameter pack is a collection of zero or more arbitrary types. How to use it? Cleverly.')
The first way: as a set of argument types of functions or methods. This is done like this:
template<typename... Types> void just_do_nothing_for_no_reason(Types... args) { // indeed } Here Types... args is another special syntactic construction ( function parameter pack ), which expands into the corresponding parameter pack of the function argument chain. Since C ++ supports autodetection of template function arguments, this function can now be called with any number of arguments of any type.Well, then what? What can you do with all these arguments?
First, you can simply use further, as the types of other functions or templates with a variable number of arguments:
template<typename... Types> tuple<Types...> make_tuple(Types... args) { tuple<Types...> result(args...); return result; } Types... args we already know. args... is another special construction ( parameter pack expansion ), which in this case will be expanded into a list of function arguments separated by a comma. So, if you make a call to make_tuple(1, 1.f, '1') somewhere in the code, then a function of the make_tuple(1, 1.f, '1') will be created and called tuple<int, float, char> make_tuple(int a1, float a2, char a3) { tuple<int, float, char> result(a1, a2, a3); return result; } Secondly, it can be used in more complex transformations. In fact, the parameter pack expansion supports more than just the substitution of everything and everything, separated by commas. So, you can easily implement the following function:
template<typename... Types> std::tuple<Types...> just_double_everything(Types... args) { std::tuple<Types...> result((args * 2)...); // OMG return result; } Iiii - yes, you guessed it! The construction ((args * 2)...) will unfold in (a1 * 2, a2 * 2, a3 * 2) .And finally, thirdly (and in the most banal), argument lists can be used in recursion:
template<typename T> std::ostream& print(std::ostream& where, const T& what) { return where << what; } template<typename T, typename... Types> std::ostream& print(std::ostream& where, const T& what, const Types& ... other) { return print(where << what << ' ', other...); } The output is type-safe printf - definitely worth it!With the help of a certain amount of patterned magic, one can learn how to extract from packs the type and value by number and perform other machinations. An example under the spoiler.
Listing tuples
Here we see the not yet mentioned, but quite easy to understand command
So, the whole point of the line
Moral: pack expansion is a killer tool.
template<int ...> struct seq { }; // template<int N, int... S> // Python' range() struct make_range : make_range<N-1, N-1, S...> { }; template<int ...S> struct make_range<0, S...> { typedef seq<S...> result; }; template<typename... Types, int... range> std::ostream& operator_shl_impl( std::ostream& out, const std::tuple<Types...>& what, const seq<range...> /* a dummy argument */ ) { return print(out, std::get<range>(what)...); } template<typename... Types> std::ostream& operator<<(std::ostream& out, const std::tuple<Types...>& what) { using range = typename make_range<sizeof...(Types)>::result; return operator_shl_impl(out, what, range()); } Here we see the not yet mentioned, but quite easy to understand command
sizeof...(Types) - it returns the number of types in the parameter pack. By the way, it can be implemented independently.So, the whole point of the line
print(out, std::get<range>(what)...); It does nothing but calls a function with arguments from the tuple . Just think! It is for this focus that we needed a list of numbers from 0 to (n - 1) - it is thanks to him that this line unfolds into something like print(out, std::get<0>(what), std::get<1>(what), std::get<2>(what)); Write the list generator from (n - 1) to 0 - and you will be able to expand the tuples in one line: auto reversed_tuple = std::make_tuple(std::get<rev_range>(my_tuple)...); Moral: pack expansion is a killer tool.
Long arithmetic
We begin our implementation of long arithmetic. First, let's define the main class:
template<uint32_t... digits> struct BigUnsigned { static const size_t length = sizeof...(digits); // }; using Zero = BigUnsigned< >; using One = BigUnsigned<1>; In the best traditions of computation at the stage of compilation in C ++, all, in fact, the data are not stored here, but are the direct arguments of the template. C ++ will distinguish the implementation of the BigUnsigned class with different sets of parameters, due to which we will be able to implement our calculations. We agree that the first parameter will contain the lower 32 bits of our long number, and the last one will contain the most significant 32 bits, including, possibly, leading zeros (personally, I see this as the most logical solution).
Before we deal with the implementation of addition, let's define the concatenation operation on our long numbers. Using the example of this operation, we will introduce the standard tactics that we will use in the future.
So, we define an operation on two types:
template<class A, class B> struct Concatenate { using Result = void; }; We mean that these two types will be BigUnsigned implementations. We implement the operation for them: template<uint32_t... a, uint32_t... b> struct Concatenate<BigUnsigned<a...>, BigUnsigned<b...>> { // >> - C++11 using Result = BigUnsigned<a..., b...>; // ! ! }; It is equally trivial to implement bit operations, for example, (very naive) xor:
template<class A, class B> struct Xor; template<uint32_t... a, uint32_t... b> struct Xor<BigUnsigned<a...>, BigUnsigned<b...>> { using Result = BigUnsigned< (a^b)... >; // , a b }; Now, actually, addition. Do not go anywhere - you have to use recursion. Define the main class and recursion base:
template<class A, class B> struct Sum; template<class A> struct Sum<Zero, A> { using Result = A; }; template<class A> struct Sum< A, Zero> { using Result = A; }; // , : template< > struct Sum<Zero, Zero> { using Result = Zero; }; Now - the main calculations:
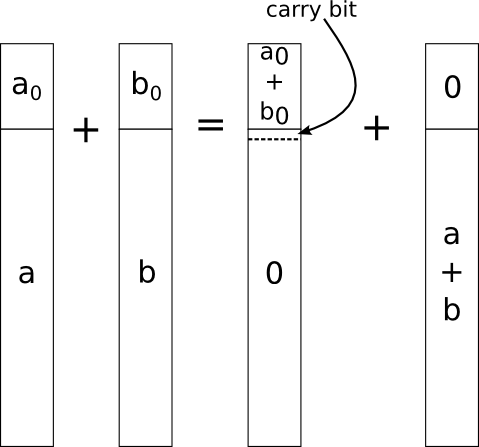
template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail> struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> { static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0; using Result = typename Concatenate< BigUnsigned<a_0 + b_0>, typename Sum< typename Sum< BigUnsigned<a_tail...>, BigUnsigned<b_tail...> >::Result, BigUnsigned<carry> >::Result >::Result; }; So what happened.
View template
template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail> struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> { we need to separate the least significant digits of long numbers from all the older ones. If we used a more general pattern template<uint32_t a..., uint32_t b...> struct Sum<BigUnsigned<a...>, BigUnsigned<b...>> { , it would not be so easy to do this, and we would need some more supporting structures. (But one could write them wisely and subsequently realize the multiplication of Karatsuba, nya!)Next, the string
static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0; calculates a so-called carry bit, indicating whether an overflow occurred in the current bit or not. (Instead of the UINT32_MAX constant, UINT32_MAX can and should use std :: numeric_limits .)Finally, the final calculation finds the result, applying recursion by the rule

Well, you can test! The calculations themselves will look something like this:
using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { // ... } Compiled! It started! But ... how do you know the value of C? How, actually, to test?
Easy way: let's call an error at compile time. For example, we write in main
int main(int argc, char** argv) { C::entertain_me(); } When trying to compile such code, we get a logical error:
static_bignum.cpp: «int main(int, char**)»: static_bignum.cpp:32:5: : «entertain_me» «C {aka static_bignum::BigUnsigned<0, 1>}» C::entertain_me(); ^ However, this whining about the g ++ error gave us the main secret - now we see that C is equal to static_bignum::BigUnsigned<0, 1> , that is, 2 32 - everything came together!A less simple way: let's write a function that will generate a string with a binary representation of a given number. The stock will look something like this:
template<class A> struct BinaryRepresentation; template<uint32_t a_0, uint32_t... a> struct BinaryRepresentation<BigUnsigned<a_0, a...>> { static std::string str(void) { // ... } }; We use the standard object std :: bitset to print the current 32 bits at each stage: template<class A> struct BinaryRepresentation; template<uint32_t a_0, uint32_t... a> struct BinaryRepresentation<BigUnsigned<a_0, a...>> { static std::string str(void) { std::bitset<32> bset(a_0); return BinaryRepresentation<BigUnsigned<a...>>::str() + bset.to_string(); } }; It remains only to specify the base recursion: template<> struct BinaryRepresentation<Zero> { static std::string str(void) { return "0b"; // Oppa Python Style } }; The new version of our primitive test will look like
using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { std::cout << BinaryRepresentation<C>::str() << std::endl; } and give us just a stunning readability response 0b00000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000 However, a careful calculation of the number of zeros can be sure that it is still 2 32 !The difficult, but most convincing way - the derivation of a decimal representation - will require some work from us, namely the implementation of the division operation.
For this we need certain, uh, prerequisites.
Implementation of the subtraction
template<class A, class B> struct Difference; struct OverflowError {}; // - ( ) // -- : template<> struct Difference<Zero, Zero> { using Result = Zero; }; template<uint32_t n, uint32_t... tail> // -- struct Difference<BigUnsigned<n, tail...>, Zero> { using Result = BigUnsigned<n, tail...>; }; template<uint32_t n, uint32_t... tail> // -- struct Difference<Zero, BigUnsigned<n, tail...>> { using Result = OverflowError; }; template<class A> struct Difference<OverflowError, A> { using Result = OverflowError; }; template<class A> struct Difference<A, OverflowError> { using Result = OverflowError; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Difference<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...> > { using A = BigUnsigned<a_n, a_tail...>; // using B = BigUnsigned<b_n, b_tail...>; using C = typename Difference<BigUnsigned<a_tail...>, BigUnsigned<b_tail...>>::Result; using Result_T = typename std::conditional< // ? a_n >= b_n, C, typename Difference<C, One>::Result >::type; using Result = typename std::conditional< // a_n == b_n && std::is_same<Result_T, Zero>::value, Zero, typename Concatenate< BigUnsigned<a_n - b_n>, Result_T >::Result >::type; }; Implementation of bit shifts
Define the main classes and set the recursion base:
A small shift is a bit more delicate work:
Finally, just a shift:
template<class A, size_t shift> struct ShiftLeft; template<class A, size_t shift> struct ShiftRight; template<class A, size_t shift> struct BigShiftLeft; template<class A, size_t shift> struct BigShiftRight; template<class A, size_t shift> struct SmallShiftLeft; template<class A, size_t shift> struct SmallShiftRight; template<size_t shift> struct BigShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct BigShiftRight <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftRight<Zero, shift> { using Result = Zero; static const uint32_t carry = 0; }; template<uint32_t... a> struct BigShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct BigShiftRight <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftRight<BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; static const uint32_t carry = 0; }; I decided that it is logical to divide any bit shift into the alternate use of small (shift less than 32 bits) and large (shift is a multiple of 32 bits), since their implementations differ significantly. So a big shift: template<uint32_t... a, size_t shift> struct BigShiftLeft<BigUnsigned<a...>, shift> { using Result = typename Concatenate< BigUnsigned<0>, typename BigShiftLeft< BigUnsigned<a...>, shift - 1 >::Result >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct BigShiftRight<BigUnsigned<a_0, a_tail...>, shift> { using Result = typename BigShiftRight< BigUnsigned<a_tail...>, shift - 1 >::Result; }; Here, shift denotes a shift of 32 ⋅ shift bits, and the operation itself simply “eats” or adds in turn entire 32-bit words.A small shift is a bit more delicate work:
template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftLeft<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits"); static const uint32_t carry = a_0 >> (32 - shift); using Result = typename Concatenate< BigUnsigned<(a_0 << shift)>, typename Sum< // Or Xor, Sum typename SmallShiftLeft<BigUnsigned<a_tail...>, shift>::Result, BigUnsigned<carry> >::Result >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftRight<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits"); static const uint32_t carry = a_0 << (32 - shift); using Result = typename Concatenate< BigUnsigned<(a_0 >> shift) | SmallShiftRight<BigUnsigned<a_tail...>, shift>::carry>, typename SmallShiftRight<BigUnsigned<a_tail...>, shift>::Result >::Result; }; Here again you have to take care of accurate bit shifting.Finally, just a shift:
template<class A, size_t shift> struct ShiftLeft { using Result = typename BigShiftLeft< typename SmallShiftLeft<A, shift % 32>::Result, shift / 32 >::Result; }; template<class A, size_t shift> struct ShiftRight { using Result = typename SmallShiftRight< typename BigShiftRight<A, shift / 32>::Result, shift % 32 >::Result; }; As promised, he just correctly uses the big and small shifts.Implementing Comparison Operations
template<class A, class B> struct GreaterThan; template<class A, class B> struct GreaterThanOrEqualTo; template<class A> struct GreaterThan<Zero, A> { static const bool value = false; }; template<class A> struct GreaterThanOrEqualTo<Zero, A> { static const bool value = false; }; template< > struct GreaterThanOrEqualTo<Zero, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThanOrEqualTo<BigUnsigned<n, tail...>, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThan<BigUnsigned<n, tail...>, Zero> { static const bool value = n > 0 || GreaterThan<BigUnsigned<tail...>, Zero>::value; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThan<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n > b_n); }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThanOrEqualTo<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n >= b_n); }; template<class A, class B> struct LessThan { static const bool value = !GreaterThanOrEqualTo<A, B>::value; }; template<class A, class B> struct LessThanOrEqualTo { static const bool value = !GreaterThan<A, B>::value; }; So division. Let's start as expected: with the definition of classes and the task of the base of recursion.
template<class A, class B> struct Division; template<class A> struct Division<A, Zero> { using Quotient = DivisionByZeroError; using Residue = DivisionByZeroError; }; template<uint32_t n, uint32_t... tail> struct Division<BigUnsigned<n, tail...>, One> { using Quotient = BigUnsigned<n, tail...>; using Residue = Zero; }; template<class A, class B> struct DummyDivision { using Quotient = Zero; using Residue = A; }; Here we have introduced an additional dummy class
struct DivisionByZeroError {} ,the only function of which is to slightly brighten up the unattractive life of a programmer,
trying to debug a template program. So, when trying to compile a program like
int main(...) { ... std::cout << BinaryRepresentation<typename Division<One, Zero>::Quotient>::str() << std::endl; ... } clang will give us a warning like static_bignum.cpp:229:18: error: implicit instantiation of undefined template 'BinaryRepresentation<DivisionByZeroError>' Why we need a mysterious class DummyDivision , we will see.So, the division algorithm itself will be the simplest (and probably rather inefficient). Let it be necessary to divide A by B. If A is less than B, then the solution is obvious: the remainder is A, the quotient is 0. (Actually, the obvious division also produces the auxiliary class
DummyDivision .) Otherwise, let Q be the result of dividing A by 2B, R is the remainder of this division, that is, A = 2BQ + R Then, obviously, A / B = 2Q + R / B ; however, since R is guaranteed to be less than 2B, then R / B is either 0 or 1. In turn, A % B = R % B , and R % B is equal to either R or R - B Actually, the code: template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Division<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { private: using A = BigUnsigned<a_n, a_tail...>; // .. .. using B = BigUnsigned<b_n, b_tail...>; using D = typename std::conditional< // : 2B GreaterThanOrEqualTo<A, B>::value, Division<A, typename SmallShiftLeft<B, 1>::Result>, DummyDivision<A, B> // ( ) >::type; using Q = typename D::Quotient; // using R = typename D::Residue; public: using Quotient = typename Sum< // 2Q (, , Q << 1) R / B typename SmallShiftLeft<Q, 1>::Result, typename std::conditional<GreaterThanOrEqualTo<R, B>::value, One, Zero>::type // <type_traits> std::conditional, // , >::Result; using Residue = typename std::conditional< GreaterThanOrEqualTo<R, B>::value, typename Difference<R, B>::Result, R >::type; }; Iiii finally decimal representation! It is clear that to print a decimal representation of a number, you can divide it for a long time by 10. The remainder of the first division will give the youngest character, the remainder of the division of the first quotient by 10 will give the second character and so on. However, we take into account that in C ++ we are not obliged to print number digit by digit; we are quite satisfied to divide the number with the remainder, for example, by 100, in order to get two signs at once. Therefore, we will divide by the largest number that enters
uint32_t , namely, by 10 9 . template<class A> struct DecimalRepresentation; template<> struct DecimalRepresentation<Zero> { static inline std::string str(void) { return "0"; } }; template<class A> struct Digit; // , template<> struct Digit<Zero> { static const uint32_t value = 0; }; template<uint32_t digit, uint32_t... tail> struct Digit<BigUnsigned<digit, tail...>> { static const uint32_t value = digit; }; template<uint32_t n, uint32_t... tail> struct DecimalRepresentation<BigUnsigned<n, tail...>> { private: static const uint32_t modulo = 1000000000UL; static const uint32_t modulo_log = 9; using D = Division<BigUnsigned<n, tail...>, BigUnsigned<modulo>>; using Q = typename D::Quotient; using R = typename D::Residue; static_assert(Digit<R>::value < modulo, "invalid division by power of 10"); public: static std::string str(void) { // C++ , . // , . std::string stail = DecimalRepresentation<Q>::str(); // if(stail == "0") stail = ""; std::string curr = std::to_string(Digit<R>::value); // if(stail != "") while(curr.size() < modulo_log) curr = "0" + curr; return stail + curr; } }; And finally, our code
using A = BigUnsigned<0xFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { std::cout << DecimalRepresentation<C>::str() << std::endl; } gives out
4294967296 , which is exactly equal to 2 32 !All code together
#include <cstdint> #include <bitset> #include <iostream> #include <algorithm> #include <type_traits> template<uint32_t... digits> struct BigUnsigned { static const size_t length = sizeof...(digits); }; using Zero = BigUnsigned< >; using One = BigUnsigned<1>; template<class A, class B> struct Concatenate { using Result = void; }; template<uint32_t... a, uint32_t... b> struct Concatenate<BigUnsigned<a...>, BigUnsigned<b...>> { // >> - C++11 using Result = BigUnsigned<a..., b...>; }; template<class A, class B> struct Sum; template<class A> struct Sum<Zero, A> { using Result = A; }; template<class A> struct Sum< A, Zero> { using Result = A; }; // , : template< > struct Sum<Zero, Zero> { using Result = Zero; }; template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail> struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> { static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0; using Result = typename Concatenate< BigUnsigned<a_0 + b_0>, typename Sum< typename Sum< BigUnsigned<a_tail...>, BigUnsigned<b_tail...> >::Result, BigUnsigned<carry> >::Result >::Result; }; template<class A> struct BinaryRepresentation; template<uint32_t a_0, uint32_t... a> struct BinaryRepresentation<BigUnsigned<a_0, a...>> { static std::string str(void) { std::bitset<32> bset(a_0); return BinaryRepresentation<BigUnsigned<a...>>::str() + bset.to_string(); } }; template<> struct BinaryRepresentation<Zero> { static std::string str(void) { return "0b"; // Oppa Python Style } }; template<class A, class B> struct Difference; struct OverflowError {}; template<> struct Difference<Zero, Zero> { using Result = Zero; }; template<uint32_t n, uint32_t... tail> struct Difference<BigUnsigned<n, tail...>, Zero> { using Result = BigUnsigned<n, tail...>; }; template<uint32_t n, uint32_t... tail> struct Difference<Zero, BigUnsigned<n, tail...>> { using Result = OverflowError; }; template<class A> struct Difference<OverflowError, A> { using Result = OverflowError; }; template<class A> struct Difference<A, OverflowError> { using Result = OverflowError; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Difference<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...> > { using A = BigUnsigned<a_n, a_tail...>; // using B = BigUnsigned<b_n, b_tail...>; using C = typename Difference<BigUnsigned<a_tail...>, BigUnsigned<b_tail...>>::Result; using Result_T = typename std::conditional< // ? a_n >= b_n, C, typename Difference<C, One>::Result >::type; using Result = typename std::conditional< // a_n == b_n && std::is_same<Result_T, Zero>::value, Zero, typename Concatenate< BigUnsigned<a_n - b_n>, Result_T >::Result >::type; }; template<class A, size_t shift> struct ShiftLeft; template<class A, size_t shift> struct ShiftRight; template<class A, size_t shift> struct BigShiftLeft; template<class A, size_t shift> struct BigShiftRight; template<class A, size_t shift> struct SmallShiftLeft; template<class A, size_t shift> struct SmallShiftRight; template<size_t shift> struct BigShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct BigShiftRight <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftLeft <Zero, shift> { using Result = Zero; }; template<size_t shift> struct SmallShiftRight<Zero, shift> { using Result = Zero; static const uint32_t carry = 0; }; template<uint32_t... a> struct BigShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct BigShiftRight <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; }; template<uint32_t... a> struct SmallShiftRight<BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; static const uint32_t carry = 0; }; template<uint32_t... a, size_t shift> struct BigShiftLeft<BigUnsigned<a...>, shift> { using Result = typename Concatenate< BigUnsigned<0>, typename BigShiftLeft< BigUnsigned<a...>, shift - 1 >::Result >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct BigShiftRight<BigUnsigned<a_0, a_tail...>, shift> { using Result = typename BigShiftRight< BigUnsigned<a_tail...>, shift - 1 >::Result; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftLeft<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits"); static const uint32_t carry = a_0 >> (32 - shift); using Tail = typename Sum< // Or Xor, Sum typename SmallShiftLeft<BigUnsigned<a_tail...>, shift>::Result, BigUnsigned<carry> >::Result; using Result = typename std::conditional< std::is_same<Tail, BigUnsigned<0>>::value, // , (!) BigUnsigned<(a_0 << shift)>, typename Concatenate< BigUnsigned<(a_0 << shift)>, Tail >::Result >::type; }; template<uint32_t a_0, uint32_t... a_tail, size_t shift> struct SmallShiftRight<BigUnsigned<a_0, a_tail...>, shift> { static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits"); static const uint32_t carry = a_0 << (32 - shift); using Result = typename Concatenate< BigUnsigned<(a_0 >> shift) | SmallShiftRight<BigUnsigned<a_tail...>, shift>::carry>, typename SmallShiftRight<BigUnsigned<a_tail...>, shift>::Result >::Result; }; template<class A, size_t shift> struct ShiftLeft { using Result = typename BigShiftLeft< typename SmallShiftLeft<A, shift % 32>::Result, shift / 32 >::Result; }; template<class A, size_t shift> struct ShiftRight { using Result = typename SmallShiftRight< typename BigShiftRight<A, shift / 32>::Result, shift % 32 >::Result; }; template<class A, class B> struct GreaterThan; template<class A, class B> struct GreaterThanOrEqualTo; template<class A> struct GreaterThan<Zero, A> { static const bool value = false; }; template<class A> struct GreaterThanOrEqualTo<Zero, A> { static const bool value = false; }; template< > struct GreaterThanOrEqualTo<Zero, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThanOrEqualTo<BigUnsigned<n, tail...>, Zero> { static const bool value = true; }; template<uint32_t n, uint32_t... tail> struct GreaterThan<BigUnsigned<n, tail...>, Zero> { static const bool value = n > 0 || GreaterThan<BigUnsigned<tail...>, Zero>::value; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThan<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n > b_n); }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct GreaterThanOrEqualTo<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { using A_tail = BigUnsigned<a_tail...>; using B_tail = BigUnsigned<b_tail...>; static const bool value = GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n >= b_n); }; template<class A, class B> struct LessThan { static const bool value = !GreaterThanOrEqualTo<A, B>::value; }; template<class A, class B> struct LessThanOrEqualTo { static const bool value = !GreaterThan<A, B>::value; }; struct DivisionByZeroError { }; template<class A, class B> struct Division; template<class A> struct Division<A, Zero> { using Quotient = DivisionByZeroError; using Residue = DivisionByZeroError; }; template<uint32_t n, uint32_t... tail> struct Division<BigUnsigned<n, tail...>, One> { using Quotient = BigUnsigned<n, tail...>; using Residue = Zero; }; template<class A, class B> struct DummyDivision { using Quotient = Zero; using Residue = A; }; template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail> struct Division<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> { private: using A = BigUnsigned<a_n, a_tail...>; using B = BigUnsigned<b_n, b_tail...>; using D = typename std::conditional< GreaterThanOrEqualTo<A, B>::value, Division<A, typename SmallShiftLeft<B, 1>::Result>, DummyDivision<A, B> >::type; using Q = typename D::Quotient; using R = typename D::Residue; public: using Quotient = typename Sum< typename SmallShiftLeft<Q, 1>::Result, typename std::conditional<GreaterThanOrEqualTo<R, B>::value, One, Zero>::type >::Result; using Residue = typename std::conditional< GreaterThanOrEqualTo<R, B>::value, typename Difference<R, B>::Result, R >::type; }; template<class A> struct DecimalRepresentation; template<> struct DecimalRepresentation<Zero> { static inline std::string str(void) { return "0"; } }; template<class A> struct Digit; template<> struct Digit<Zero> { static const uint32_t value = 0; }; template<uint32_t digit, uint32_t... tail> struct Digit<BigUnsigned<digit, tail...>> { static const uint32_t value = digit; }; template<uint32_t n, uint32_t... tail> struct DecimalRepresentation<BigUnsigned<n, tail...>> { private: static const uint32_t modulo = 1000000000UL; static const uint32_t modulo_log = 9; using D = Division<BigUnsigned<n, tail...>, BigUnsigned<modulo>>; using Q = typename D::Quotient; using R = typename D::Residue; static_assert(Digit<R>::value < modulo, "invalid division by power of 10"); public: static std::string str(void ){ std::string stail = DecimalRepresentation<Q>::str(); if(stail == "0") stail = ""; std::string curr = std::to_string(Digit<R>::value); if(stail != "") while(curr.size() < modulo_log) curr = "0" + curr; return stail + curr; } }; using A = BigUnsigned<0xFFFFFFFFULL>; using B = One; using C = Sum<A, B>::Result; int main(int argc, char** argv) { std::cout << DecimalRepresentation<C>::str() << std::endl; } -, , .
: (), ,
. ,
BigSigned<int, uint32_t...>.
-, . , , .
( , , , ,
.) , .
-, , —
. — , .
Source: https://habr.com/ru/post/248897/
All Articles