Non-recursive permutation generation algorithm
The non-recursive algorithm proposed below is somewhat different from those described in the book by Lipsky [1] and found by me in the Russian segment of the Internet. I hope it will be interesting.
Briefly setting the problem. There is a lot of dimension N. You need to get all N! possible permutations.
Further, for simplicity, we use integers (1..N) as the set. Instead of numbers, you can use any objects, because there are no operations to compare the elements of a set in the algorithm.
To store intermediate data, we will form the following data structure:
and fill it with the original values
The element number in the masiv array will be referred to as the level below.
In the list of the first level we enter all the elements of the set At the first level, the list dimension is N and the list itself does not change throughout the course of the algorithm. During the initial filling, all pointers in the array are set to the first item in the list.
At each next level, its list is formed based on the list of the previous level, but without one element, which is marked with a pointer. At the penultimate level (N-2), the list contains three elements. At the last level (N-1), the list contains two elements. The list of the lower level is formed as a list of the previous level without an element pointed to by the pointer of the previous level.
As a result of the initial filling, the first two permutations were obtained. This is a common array formed at the upper levels (1 ... (N-2)) from the list elements that are pointed to by pointers.
and from the list of the last level - two pairs of elements in a different order (two tails 1 2 and 2 1)
All further permutations are also formed, always from the penultimate level (N-2),
The order of obtaining subsequent permutations is that, being at the penultimate level (N-2) and having formed two permutations, we are trying to increase the pointer of the selected element by 1.
If this is possible, then at the last level we change the list and repeat.
If it is not possible to increase the pointer at the penultimate level (all possible options have been enumerated), then we rise to the level at which increasing the pointer (moving to the right) is possible. Algorithm end condition - the pointer at the first level goes beyond N.
After moving the pointer to the right, we change the list below it and move down to the penultimate level (N-2), also updating the lists and setting the pointers of the selected item to 1.
The operation of the algorithm is presented more clearly and clearly in the figure below (for the dimension of the set N = 5). The number in the picture corresponds to the level in the description. It is even possible that apart from the picture, nothing is needed to understand the algorithm.
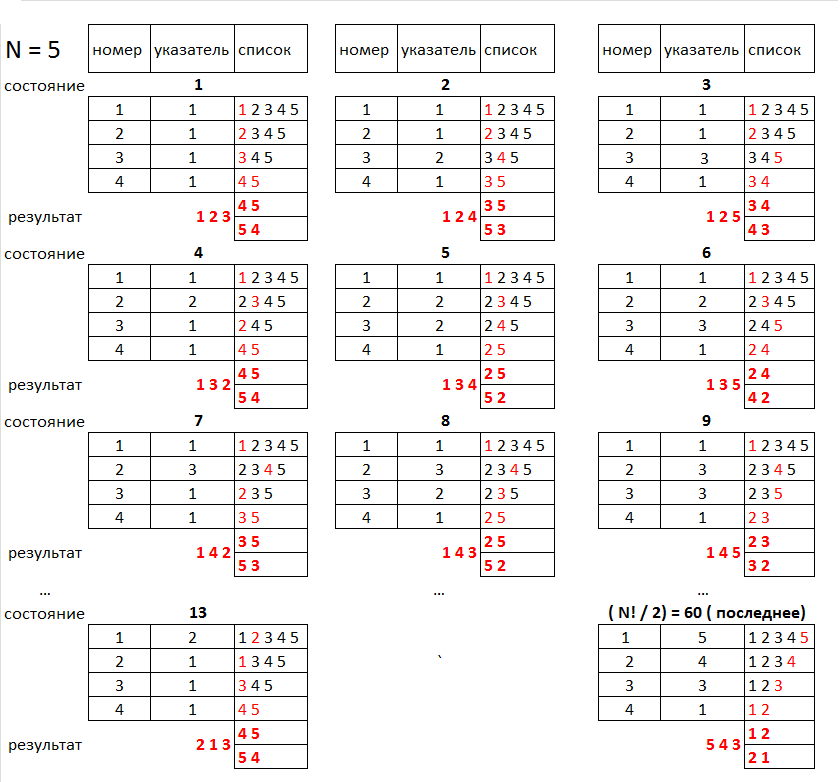
Of course, when implementing the algorithm, it was possible to use the usual two-dimensional array, especially since for small N the gain of the memory capacity does not give anything, and for large N we can not wait for the algorithm to finish.
One way to implement the algorithm on VBA is below. To start it, you can create an Excel workbook with macros, create a module on the VB developer tab, and copy the text into the module. After running generate (), all permutations will be displayed on Sheet1.
References:
[1] V.Lipsky. Combinatorics for programmers. -Moscow, Mir publishing house, 1988.
Briefly setting the problem. There is a lot of dimension N. You need to get all N! possible permutations.
Further, for simplicity, we use integers (1..N) as the set. Instead of numbers, you can use any objects, because there are no operations to compare the elements of a set in the algorithm.
To store intermediate data, we will form the following data structure:
type dtree ukaz as integer ' spisok() as integer ' end type and fill it with the original values
Dim masiv(N-) As dtree ' = N-1 For ii = 1 To N - 1 masiv(ii).ukaz = 1 ReDim masiv(ii).spisok(N + 1 - ii) ' For kk = 1 To (N + 1 - ii) masiv(ii).spisok(kk) = kk + ii - 1 Next Next The element number in the masiv array will be referred to as the level below.
In the list of the first level we enter all the elements of the set At the first level, the list dimension is N and the list itself does not change throughout the course of the algorithm. During the initial filling, all pointers in the array are set to the first item in the list.
At each next level, its list is formed based on the list of the previous level, but without one element, which is marked with a pointer. At the penultimate level (N-2), the list contains three elements. At the last level (N-1), the list contains two elements. The list of the lower level is formed as a list of the previous level without an element pointed to by the pointer of the previous level.
As a result of the initial filling, the first two permutations were obtained. This is a common array formed at the upper levels (1 ... (N-2)) from the list elements that are pointed to by pointers.
For ii = 1 To N-2 massiv(ii).spisok(ukaz) Next and from the list of the last level - two pairs of elements in a different order (two tails 1 2 and 2 1)
+ massiv(N-1).spisok(1) + massiv(N-1).spisok(2) + massiv(N-1).spisok(2) + massiv(N-1).spisok(1) All further permutations are also formed, always from the penultimate level (N-2),
The order of obtaining subsequent permutations is that, being at the penultimate level (N-2) and having formed two permutations, we are trying to increase the pointer of the selected element by 1.
If this is possible, then at the last level we change the list and repeat.
If it is not possible to increase the pointer at the penultimate level (all possible options have been enumerated), then we rise to the level at which increasing the pointer (moving to the right) is possible. Algorithm end condition - the pointer at the first level goes beyond N.
After moving the pointer to the right, we change the list below it and move down to the penultimate level (N-2), also updating the lists and setting the pointers of the selected item to 1.
The operation of the algorithm is presented more clearly and clearly in the figure below (for the dimension of the set N = 5). The number in the picture corresponds to the level in the description. It is even possible that apart from the picture, nothing is needed to understand the algorithm.

Of course, when implementing the algorithm, it was possible to use the usual two-dimensional array, especially since for small N the gain of the memory capacity does not give anything, and for large N we can not wait for the algorithm to finish.
One way to implement the algorithm on VBA is below. To start it, you can create an Excel workbook with macros, create a module on the VB developer tab, and copy the text into the module. After running generate (), all permutations will be displayed on Sheet1.
VBA for Excel
Option Explicit Type dtree tek_elem_ukaz As Integer spisok() As Integer End Type Dim masiv() As dtree Dim start_print As Integer Dim N As Integer Sub generate() Dim ii As Integer, kk As Integer, jj As Integer Dim uroven As Integer 1.Cells.Clear N = 5 start_print = 1 ReDim masiv(N - 1) ' For ii = 1 To N - 1 masiv(ii).tek_elem_ukaz = 1 ReDim masiv(ii).spisok(N + 1 - ii) For kk = 1 To (N + 1 - ii) masiv(ii).spisok(kk) = kk + ii - 1 Next Next uroven = N - 2 Do ' Call print_rezult(uroven) ' If masiv(uroven).tek_elem_ukaz <= (N - uroven) Then ' ' masiv(uroven).tek_elem_ukaz = masiv(uroven).tek_elem_ukaz + 1 ' Call zap_niz(uroven) Else ' , Do While uroven > 1 And masiv(uroven).tek_elem_ukaz > (N - uroven) uroven = uroven - 1 Loop If uroven = 1 And masiv(1).tek_elem_ukaz = N Then MsgBox "stop calc" Exit Sub ' End If ' masiv(uroven).tek_elem_ukaz = masiv(uroven).tek_elem_ukaz + 1 Call zap_niz(uroven) ' Do While uroven < N - 2 uroven = uroven + 1 masiv(uroven + 1).tek_elem_ukaz = 1 ' For kk = 2 To N - uroven + 1 masiv(uroven + 1).spisok(kk - 1) = masiv(uroven).spisok(kk) Next Loop End If Loop End Sub Sub print_rezult(ukaz As Integer) Dim ii As Integer For ii = 1 To ukaz With masiv(ii) 1.Cells(start_print, ii) = .spisok(.tek_elem_ukaz) 1.Cells(start_print + 1, ii) = .spisok(.tek_elem_ukaz) End With Next With masiv(ukaz + 1) 1.Cells(start_print, ukaz + 1) = .spisok(1) 1.Cells(start_print, ukaz + 2) = .spisok(2) start_print = start_print + 1 1.Cells(start_print, ukaz + 1) = .spisok(2) 1.Cells(start_print, ukaz + 2) = .spisok(1) start_print = start_print + 1 End With End Sub Sub zap_niz(ukaz As Integer) ' Dim ii As Integer, wsp1 As Integer ' wsp1 = masiv(ukaz).tek_elem_ukaz masiv(ukaz + 1).tek_elem_ukaz = 1 ' For ii = 1 To wsp1 - 1 masiv(ukaz + 1).spisok(ii) = masiv(ukaz).spisok(ii) Next For ii = wsp1 + 1 To N - ukaz + 1 masiv(ukaz + 1).spisok(ii - 1) = masiv(ukaz).spisok(ii) Next End Sub References:
[1] V.Lipsky. Combinatorics for programmers. -Moscow, Mir publishing house, 1988.
')
Source: https://habr.com/ru/post/248493/
All Articles