Binary operations on unordered sets
In this publication I will carry out the algorithmization of operations on arrays, as well as talk about the operations themselves.
The intersection of two arrays A and B is an array with only those elements A and B that simultaneously belong to both arrays, without duplicates.

')
The complexity of the algorithm is O (m * n) , where m and n are the lengths of the input arrays A and B, respectively.
The difference between two arrays A and B is an array with elements A that do not coincide with elements B , without duplicates.

The complexity of the algorithm is O (m * n) , where m and n are the lengths of the input arrays A and B, respectively.
The union of two arrays A and B is an array with elements A and elements of array B , without duplicates.
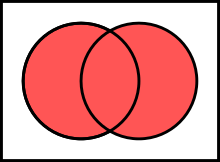
The complexity of the algorithm is O (m * n) , where m and n are the lengths of the input arrays A and B, respectively.
The symmetric difference of two arrays A and B is such an array, which includes all those elements of the first array that are not included in the second array, as well as those elements of the second array that are not included in the first array.
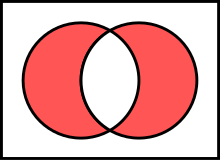
The complexity of the algorithm is O (2m * n) , where m and n are the lengths of the input arrays A and B, respectively.
In essence, this is subtraction of arrays, first A from B, then B from A.
A live example on the example of friends VKontakte. When entering links to users' pages on VKontakte, the service returns all intersections of arrays of friends of users (intersections are common friends of users).
Content
- I. Intersection of arrays
- Ii. Array Difference
- Iii. Array combining
- Iv. Symmetric array difference
- Conclusion
I. Intersection of arrays
The intersection of two arrays A and B is an array with only those elements A and B that simultaneously belong to both arrays, without duplicates.

')
The complexity of the algorithm is O (m * n) , where m and n are the lengths of the input arrays A and B, respectively.
function intersection(A, B) { var m = A.length, n = B.length, c = 0, C = []; for (var i = 0; i < m; i++) { var j = 0, k = 0; while (B[j] !== A[ i ] && j < n) j++; while (C[k] !== A[ i ] && k < c) k++; if (j != n && k == c) C[c++] = A[ i ]; } return C; } Example:
intersection ([1,2,3,7,9],[4,5,7,2,1,5]); // [1,2,7] Ii. Array Difference
The difference between two arrays A and B is an array with elements A that do not coincide with elements B , without duplicates.

The complexity of the algorithm is O (m * n) , where m and n are the lengths of the input arrays A and B, respectively.
function diff(A, B) { var M = A.length, N = B.length, c = 0, C = []; for (var i = 0; i < M; i++) { var j = 0, k = 0; while (B[j] !== A[ i ] && j < N) j++; while (C[k] !== A[ i ] && k < c) k++; if (j == N && k == c) C[c++] = A[ i ]; } return C; } Example:
diff([1,2,3,7,9],[4,5,7,2,1,5]); // [3,9] diff([4,5,7,2,1,5], [1,2,3,7,9]); // [4,5] Iii. Array combining
The union of two arrays A and B is an array with elements A and elements of array B , without duplicates.

The complexity of the algorithm is O (m * n) , where m and n are the lengths of the input arrays A and B, respectively.
function sum(A, B) { var M = A.length, N = B.length, count = 0, C = []; C = A; count = M; var cnt = 0; for (var i=0;i<N;i++) { var plus = false; for (var j=0;j<M;j++) if (C[j] == B[i]) {plus = true; break;} if (plus === false) C[count++] = B[i]; } return C; } Example:
sum([1,2,3,7,9],[4,5,7,2,1,5]); // [1,2,3,7,9,4,5] sum([4,5,7,2,1,5],[1,2,3,7,9]); // [4,5,7,2,1,5,3,9] Iv. Symmetric array difference
The symmetric difference of two arrays A and B is such an array, which includes all those elements of the first array that are not included in the second array, as well as those elements of the second array that are not included in the first array.

The complexity of the algorithm is O (2m * n) , where m and n are the lengths of the input arrays A and B, respectively.
In essence, this is subtraction of arrays, first A from B, then B from A.
function symmetricDiff(A,B) { var M = A.length, N = B.length, c = 0, C = []; for (var i = 0; i < M; i++) { var j = 0, k = 0; while (B[j] !== A[ i ] && j < N) j++; while (C[k] !== A[ i ] && k < c) k++; if (j == N && k == c) C[c++] = A[ i ]; } for (var i = 0; i < N; i++) { var j = 0, k = 0; while (A[j] !== B[ i ] && j < M) j++; while (C[k] !== B[ i ] && k < c) k++; if (j == M && k == c) C[c++] = B[ i ]; } return C; } Example:
symmetricDiff([1,2,3,7,9],[4,5,7,2,1,5]);// [3,9,4,5] symmetricDiff([1,2,3,4,5],[3,4,5,6,7]); // [1,2,6,7] Conclusion
A live example on the example of friends VKontakte. When entering links to users' pages on VKontakte, the service returns all intersections of arrays of friends of users (intersections are common friends of users).
Source: https://habr.com/ru/post/248229/
All Articles