The legacy of Jacob Bernoulli in Wolfram Language (Mathematica)

Translation of the post by Oleksandr Pavlyk (Oleksandr Pavlyk), " Jacob Bernoulli's Legacy in Mathematica ".
Download the translation in the form of a Mathematica document, which contains all the code used in the article, as well as additional materials, here .

January 16, 2015 marked the 360th anniversary of the birth of Jacob Bernoulli .

In [1]: =
')


Out [2] =



In [3]: =



Out [3] =



In [4]: ​​=



Out [4] =



Jacob Bernoulli became the first mathematician of the famous Bernoulli family , to which many famous mathematicians of the XVII and XVIII centuries belong.

The mathematical heritage of Jacob Bernoulli is very rich. He introduced the so-called Bernoulli numbers ( Wiki / MathWorld ), found the solution of the Bernoulli differential equation ( Wiki / MathWorld ), studied the Bernoulli process ( Wiki / MathWorld ), proved the Bernoulli inequality ( Wiki / MathWorld ), calculated the number e ( Wiki / MathWorld ), and also revealed the weak law of large numbers (Bernoulli's theorem) ( Wiki / MathWorld ).

In [5]: =



Out [5] =



The treatise of Bernoulli Ars Conjectandi ( The Art of Conjecturing - The Art of Assumption) was posthumously published in 1713, 8 years after his death, it was written in Latin, the lingua franca of his time. It is considered as a fundamental work on probability theory. Its importance is indicated, in particular, by the fact that it was translated into French by G. Le Roy in 1801 and, recently, into English by ED Sylla in 2005.

Ars Conjectandi consists of 4 parts. The first part reproduces the work of Christian Huygens De Ratiociniis in Ludo Aleae . ( On Reasoning in Games of Chance - On the calculations in gambling) with extensive comments from Bernoulli and detailed solutions to five problems of Huygens, set at the end of Huygens' work with the answers, but without evidence. In the first part, Bernoulli also deduces the probability that among n independent tests there will be at least m successful, if the probability of success in each test is p :



The second part of “The Doctrine of Permutations and Combinations” is devoted to combinatorics and the study of curly numbers ( Wiki / MathWorld ), that is, numbers that can be represented as a set of points located on a plane in the shape of regular geometric shapes:



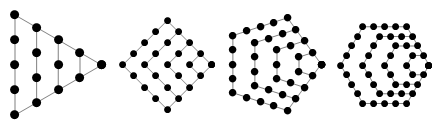
It is in this part that Bernoulli introduced the so-called Bernoulli numbers. He began by identifying the relationship for the binomial coefficients which looks like:

.

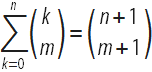In [6]: =



Out [6] =




Bernoulli knew that for a fixed value of the number m , the binomial coefficient 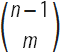is a polynomial in the variable n , namely 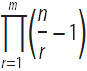. This identity allowed him to derive the values ​​of the sums of the powers of the natural numbers . He received a table of results for 0≤m≤10 .

In order to reproduce the table obtained by Bernoulli, we create a function that defines the equations for the sums of powers of natural numbers:

In [7]: =



In [8]: =



Out [8] =



In [9]: =



Out [9] =



In [10]: =



Out [10] =



Solving the resulting system of equations, we get:

In [11]: =



Out [11] =



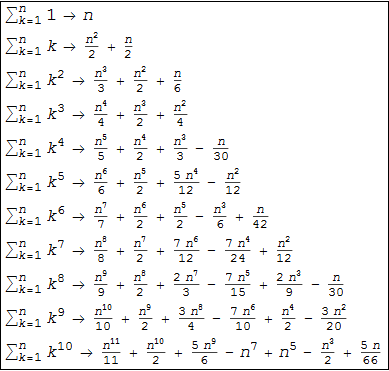
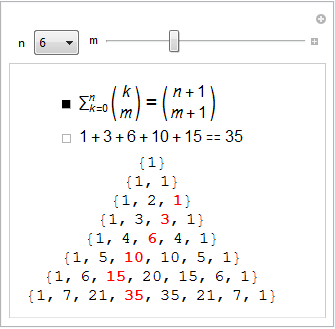
Bernoulli wrote that “He who has carefully studied the obtained sequence can continue the Table further without any additional calculations”, noting that:



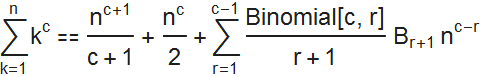
He noted that the coefficients do not depend on n , and can be calculated recursively if we substitute n == 1 into the equation above.

In [12]: =



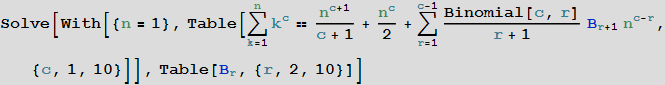
Out [12] =



These coefficients are known Bernoulli numbers, which have found their application in many areas of mathematics [for example, see the discussion Why do Bernoulli numbers everywhere? (Why are Bernoulli numbers appearing everywhere?) On mathoverflow.net]:

In [13]: =



Out [13] =



In the second part of his book, Bernoulli calculates the number of possible permutations, the number of permutations in the set with repeating elements, the number of ways to select given objects from the set, etc., which he later uses to calculate probability as the ratio of the number of favorable events to the total possible number of events .

In the third part, Bernoulli applies the results obtained in the previous two parts to solving 24 problems associated with gambling. The keynote of all these tasks is the sequence of independent results 0 and 1, which was called the “Bernoulli process”. I think that the 360th anniversary of the birth of Jacob Bernoulli is an excellent opportunity to solve his tasks in Mathematica with the help of Wolfram Language.

For example, in task 9 it is required to find the expected winning in a game of three players. Players alternately take cards (without replacement and return) from a deck of 20 cards, with 10 of them figured. When the cards run out, the winnings are distributed equally among those players who have more curly cards.

Suppose that c1 , c2 , and c3 is the number of shaped cards for each player, then the winning share of the first player will be equal to:

In [14]: =



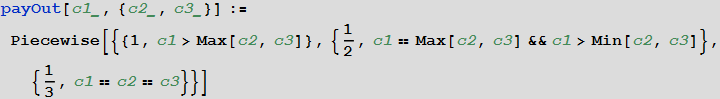
Suppose that after a deck of 20 cards was thus distributed among the players, it turned out that the first and second cards each have 7 cards, and the third one - 6. The final vector of figure cards distribution among players has a multidimensional hypergeometric distribution, which is given in Wolfram Language MultivariateHypergeometricDistribution function:

In [15]: =



In [16]: =



Out [16] =



In [17]: =



Out [17] =



This and other tasks are considered and solved in the attached document (in English. Language).

The final part of the treatise Ars Conjectandi discusses the use of probability theory in solving civil, moral, and economic issues. In this part, Bernoulli argues that probability theory reflects our incomplete knowledge of the state of the world, and, unlike the game of chance, where probability can be determined by finding the ratio of the number of favorable outcomes of some experience to their total possible number, the probability in “real” life is not can be installed a priori. Bernoulli argues that these unknown probabilities can be calculated based on the results observed in the past.

He proved the weak law of large numbers, which states that the observed frequency of success in a series of n independent tests, the probability of success in each of which is p , will approach unlimitedly p with an unlimited increase in the number of tests. Thus, we can estimate the probability with arbitrary accuracy by taking a sufficient number of tests. Thus, for any δ and ε , there is such a number n (the number of tests) that



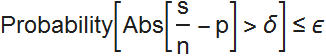
In [18]: =



Out [18] =



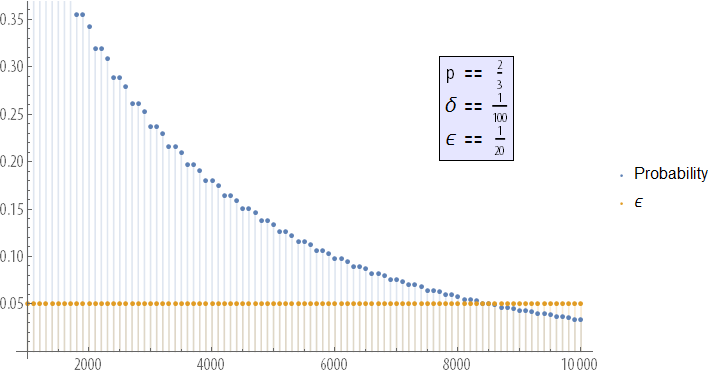
The simulated Coin Tossing experiment and the law of large numbers , created by Ian McLeod for the Wolfram Demonstrations Project, in particular, demonstrates this convergence process.

Resources for learning Wolfram Language (Mathematica) in Russian: habrahabr.ru/post/244451