Sea battle for 25 ms

Foreword

A few months ago, I decided to learn Python. As one of the test tasks required to write the game "Sea Battle". Then I didn’t do this task, but I got the idea to write “Sea battle”, where two computers would play between each other. This thought did not leave me, and I decided to dare. The result is submitted to your judgment. I would appreciate any constructive criticism.

The overall concept of the current implementation

The whole game, in fact, boils down to the fact that two instances of the Player class ask each other for the coordinates of the ships and, depending on the answer, build their own turn strategy.

The strategy for deploying ships is as follows: 2-3-4 decked are placed along the edges of the map (2 cells), 1-deck in the center (6x6 square).
')


The strategy of moves, as in a game between people: the first move is random, if you hit, then we work 4 cells around and further, if we hit again, we work two cells already on the line (two, because the ship’s maximum is 4 cells, in 2 already got, so max there are 2 more cells).

In an article on Wikipedia, everything is described in sufficient detail, so I’m not going to touch much on game logic here, especially since everyone understands something about what it is about. My only differences are: scoring for each move, cell numbering from 0 to 9.

The game uses three classes: Game, Player, Ship. Using the Game class in the current implementation is redundant, since only one copy of it is used, but this is some reserve for the future (see the list of improvements at the end of the article).

Game is responsible for the overall game logic, Player - for the strategy of moves, Ship - stores the current state of the ships and their coordinates.

Link project in github.

The main difficulties that have arisen in the development

1. Design . Write using classes or functions? What class set to use?
The main problem in the design was the tracking of various states in the game. For example, who walks now, what is the condition of the ship (hit, killed), has the game not ended, who won, etc.

2. Logic / algorithms . How to arrange the ships in accordance with the strategy, how to choose the coordinates for the course?

Overview of the most interesting parts of the code

return_shoot_state - determines the further strategy depending on the results of the current move.

def return_shoot_state(self, state, crd): """        """ if state == u'!': self.scores += 1 if not self.recomendation_pool: crd_rec = [[crd[0] - 1, crd[1]], [crd[0] + 1, crd[1]], [crd[0], crd[1] - 1], [crd[0], crd[1] + 1]] crd_rec = filter(lambda x: 0 <= x[0] <= 9 and 0 <= x[1] <= 9, crd_rec) crd_rec = filter(lambda x: x not in self.alien, crd_rec) self.succ_shoots.append(crd) self.recomendation_pool.extend(crd_rec) else: crd_s1 = self.recomendation_pool[0] crd_s2 = self.succ_shoots[0] for ind in range(2): if crd_s1[ind] != crd_s2[ind]: if crd_s1[ind] > crd_s2[ind]: crd_rec = [[crd_s1[ind]+1, crd_s1[ind]+2], [crd_s2[ind]-1, crd_s2[ind]-2]] else: crd_rec = [[crd_s1[ind]-1, crd_s1[ind]-2], [crd_s2[ind]+1, crd_s2[ind]+2]] crd_rec = filter(lambda x: 0 <= x[0] <= 9 and 0 <= x[1] <= 9, crd_rec) crd_rec = filter(lambda x: x not in self.alien, crd_rec) self.recomendation_pool.extend(crd_rec) elif state == u'!': self.scores += 1 self.recomendation_pool = [] self.succ_shoots = [] 

Important variables: recomendation_pool - a list of coordinates for future shots, succ_shoots - the last successful shot.

If we hit the ship, then, firstly, you need to accrue points for a successful shot (scores + = 1), and secondly, understand what to do next. We check the recomendation_pool if there is something there, if not, then write down 4 nearby coordinates (after filtering them along the field boundaries and the list of coordinates we shot at).



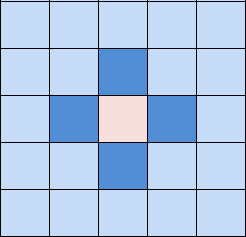
If recomendation_pool is not empty, it means that we hit the second time and it’s already not about 4 coordinates around, but about two from each edge.



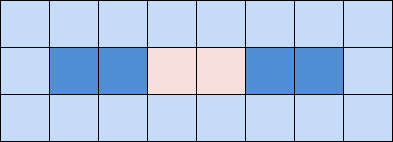
If the ship was sunk by the current shot, we consider our task completed and we clean the recommendations pool and so on. The next shot will be random.

service.gen_cord - generates all possible coordinates for each type of ships. The result of the function will be a dictionary with the following structure: {"S0": [[[x0, y0], [x1, y2], [xN0, yN1]], [[x3, y3], [x4, y4], [xN2 , yN3]], ...], “S1”: ...}, where S is the type of ship, [[x0, y0], [x1, y2], [xN0, yN1]] is the set of coordinates for the ship.

 def gen_cord(): """    """ all_comb = [[x/10, x % 10] for x in range(100)] for_1_ship = filter(lambda x: x[0] in range(2, 8) and x[1] in range(2, 8), all_comb) for_other_ship = filter(lambda x: x not in for_1_ship, all_comb) cord_comb = {1: [[x] for x in for_1_ship], 2: [], 3: [], 4: []} for ship in filter(lambda x: x != 1, cord_comb.keys()): for cord in for_other_ship: hor_direction = [cord] + [[cord[0]+x, cord[1]] for x in range(1, ship)] ver_direction = [cord] + [[cord[0], cord[1]+x] for x in range(1, ship)] for dir_d in [hor_direction, ver_direction]: for cord_d in dir_d: if cord_d not in for_other_ship: break else: cord_comb[ship].append(dir_d) return cord_comb 

Important variables: all_comb - stores the coordinates of the field in the format [[x0, y0], [x1, y1], ...]. for_1_ship is that 6x6 square for single-deck, for_other_ship is a set of coordinates for all other ships. cord_comb is a dictionary that stores all combinations of coordinates.

Ship layout

At the time of initialization of the instance of the class Player, ships are also arranged. In the class, the create_ships method is responsible for this, where the following happens:

1. For each ship (ships), a set of coordinates is selected in a pseudo-random manner (random.choice) from the available sequence of combinations of coordinates.
2. Next, a halo is generated for the set of coordinates (service.set_halo). A halo is a set of coordinates in which it will be impossible to deliver a ship later (rule: do not place ships near).



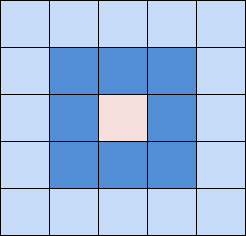
3. Then we clear the list of combinations (data_cleaner) from the list which consists of the coordinates of the ship and the halo.

Logging module

At the end of the development I discovered the logging module from the standard library. Fields for output are configured (logging.basicConfig), and working with output is no more difficult than with print.

Other

sevice.rdn_usr_name - generates random player names from a set of letters and numbers from 0 to 999.

The game ends if the opponent has Player.ships_defeat = 10, i.e. sunk all 10 ships. The counter is updated if the ship responds "Killed!".

List of improvements (TO DO)

1. Make a tournament between players, say, where there will be 1000 players. In theory, given the current running time, the entire tournament should take about 30 seconds.

2. Add a “basic algorithm” of the move, for example, go cross to cross, i.e. punch all the cells diagonally and then on. Implement several such algorithms and then assign randomly the work on them to the player. Then compare the effectiveness (for example, which gives more result to random moves or the algorithm “cross to cross”?)

3. Optimize the search engine combinations (service.gen_cord), because it is obvious that it is redundant and takes a lot of resources.

4. Implement various strategies for deploying ships and then compare which one is the most successful.

PS I would appreciate any interesting ideas.

Thank.

UPDATE (Jan 16, 2015)

The tournament is implemented + a small collection of statistics is made and this is what happens:

In the tournament there is a game for departure, i.e. if lost on the trail. step no longer get.

In order for a tournament to be without jambs, the number of players must be so that when divided, the remainder of division will always be divided by 2, and so before the number of players in the tournament is 1 (i.e., the winner). These numbers include 1024 (512, 256, 128, 64, 32, 16, 8, 4, 2).

Earlier, I assumed that the tournament would last about 30 seconds, i.e. time grows linearly depending on the number of players, but what was my surprise when the whole tournament for 1024 players is only 17 seconds. Why I’ve got 17 seconds, I don’t know, some optimization mechanisms may start working. My calculations are as follows: 1022 games lasts the entire tournament * 25 ms one game = 25.55 seconds.

Tournament statistics are kept within the following values:

1. The average number of moves (all players): 85.06,
2. The average number of moves of winning players: 85.95,
3. The average number of losing players moves: 84.17,
4. Average points scored by losers: 17.75

We can draw the following conclusions:

1. The number of moves that the winners that the losers are doing about the same.

2. The number of points is almost 18 (you need 20 to win).

Bottom line: both players play about the same and equally inefficient :) The difference of 2 points shows that victory literally breaks out of the opponent's hands in the last moves.

Conclusion: because Now, each player is guided by the same strategy. There is no particular diversity in the game. In order to make it more interesting, you need to implement various strategies for the placement of ships and the implementation of moves, which I will do at leisure in the near future.

Stay tuned for article updates.

UPDATE2 (01/16/2015)
Implemented adding a halo to the list of punched coordinates after the ship was sank (in principle, everything is fair). Statistics on the number of moves improved significantly:
1. The average number of moves (all players): 58.91,
2. The average number of moves winning players: 60.98,
3. The average number of losing players moves: 56.83,
4. Average points scored by losers: 15.37

Thanks to Meklon for the idea.

UPDATE3 (01/17/2015)

Implemented new strategies for locating ships (where there are 60 single deck cells). The result was the following: if each player uses the same strategy, then there is no difference between losers and winners, but if each player has a placement strategy assigned randomly, then it’s obvious that they lost more with my strategy (6x6 square in the center), those. if my strategy is thrown away, then everyone will play about the same. This is also not interesting. Now I will implement various moves strategies (maybe there is something super-optimal).



UPDATE4 (01.20.2015)

Added various options for making moves: random - randomly from free cells, cross - cross to cross, linear - linearly in 4 rows through one (as in the vaunted articles). An important point: the strategy of placing ships is issued for the entire tournament, but the strategy of moves is issued for each game.

Collected statistics (remember, we are talking about the turn, where 1024 players play with each other on the flight).


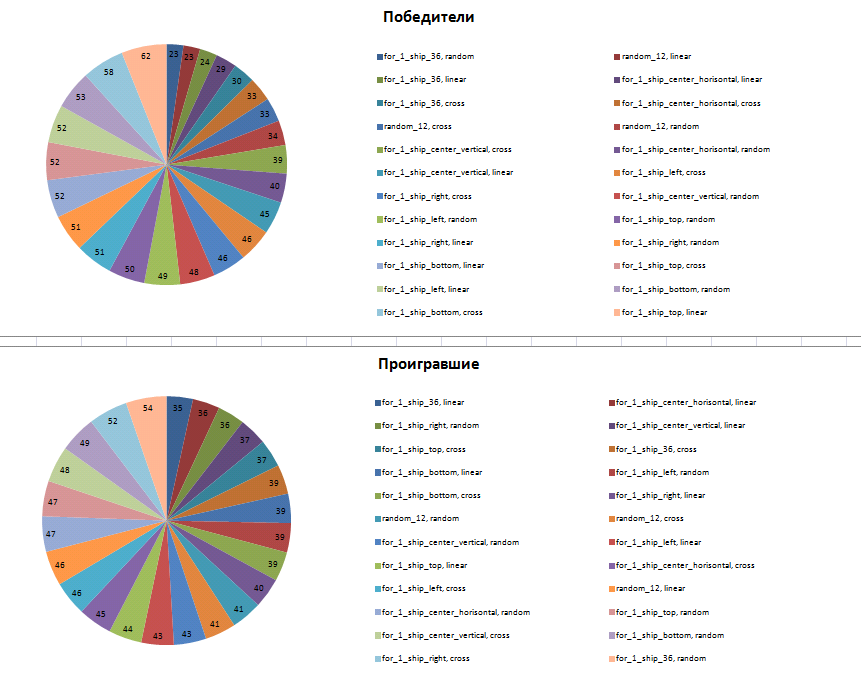
Main conclusions:
The strategy of placing single-deck ships random_12 (12 random cells are selected and we arrange ships in them) and for_1_ship_36 (6x6 field in the center) are clearly the least effective.

Uniform distribution indicates that equal among equal gave about the same result and the victory of one of them is only a random consequence.

The number of moves with the implementation of additional strategies of moves did not decrease, but the tournament time increased from 25 to 50 seconds:
1. The average number of moves (all players): 61.43,
2. The average number of moves winning players: 63.23,
3. Average number of losing players moves: 59.63,
4. Average points scored by losers: 15.93

I would be grateful if someone looked at my GitHub code and gave my recommendations for improving it.

There is only one scheduled optimization task left, but, as you know, it can be optimized indefinitely, so the article will not be updated without much need in the near future.

Thank you for your attention and may the power of Python come with you!