Dictionary implementation in Python 2.7
This article will discuss how the dictionary is implemented in Python. I will try to answer the question of why the elements of the dictionary are not ordered, to describe how the dictionaries store, add and delete their elements. I hope that the article will be useful not only to people who learn Python, but also to everyone who is interested in the internal structure and organization of data structures.
To write this article I pushed a question on the Stack Overflow.
The article discusses the implementation of CPython version 2.7. All examples were prepared in the 32-bit version of Python on a 64-bit OS, for another version the values will be different.
A dictionary in Python is an associative array, that is, it stores data in the form of pairs (key, value). A dictionary is a variable data type. This means that you can add elements to it, change them and delete them from the dictionary. It also provides the operation of finding and returning an item by key.
Initializing and adding elements:
')
Item receipt:
Deleting an item:
The keys of the dictionary can be values of only hashable types, that is, types that can have a hash (for this they must have __hash __ () method). Therefore, values of such types as a list (list), a set (set) and the dictionary itself (dict) cannot be keys of a dictionary:
The Python dictionary is implemented as a hash table. As is known, the implementation of a hash table should take into account the possibility of collisions - situations where different keys have the same hash value. There should be a way to insert and extract elements with regard to collisions. There are several ways to resolve collisions, such as the chaining method and the open addressing method. Python uses an open addressing method. The developers preferred the open addressing method to the chaining method due to the fact that it can significantly save memory on storing pointers that are used in hash tables with chains.
In the implementation under consideration, each entry (PyDictEntry) in the hash table of the dictionary consists of three elements — a hash, a key, and a value.
The structure of PyDictObject is as follows:
When creating a new dictionary object, its size is 8. This value is determined by the constant PyDict_MINSIZE. To store a hash table, the variables ma_smalltable and ma_table have been entered into PyDictObject. The pre-allocated ma_smalltable variable, PyDict_MINSIZE (that is, 8), allows small dictionaries (up to 8 PyDictEntry objects) to be stored without additional memory allocation. Experiments conducted by developers have shown that this size is quite enough for most dictionaries: small dictionaries of instances and usually small dictionaries created for passing named arguments (kwargs). The variable ma_table corresponds to ma_smalltable for small tables (that is, for tables of 8 cells). For larger tables, ma_table memory is allocated separately. The variable ma_table cannot be NULL.
If someone suddenly wants to change the value of PyDict_MINSIZE, it can be done in the source, and then rebuild Python. The value is recommended to be equal to the power of two, but not less than four.
1) Unused (me_key == me_value == NULL)
This state means that the cell does not contain and has never yet contained a pair (key, value).
After the key is inserted, the “unused” cell changes to the “active” state.
This state is the only case when me_key = NULL and is the initial state for all cells in the table.
2) Active (me_key! = NULL and me_key! = Dummy and me_value! = NULL)
Indicates that the cell contains an active pair (key, value).
After the key is removed, the cell from the “active” state changes to the “empty” state (that is, me_key = dummy,
dummy = PyString_FromString ("<dummy key>")).
This is the only state when me_value! = NULL.
3) Empty (me_key == dummy and me_value == NULL)
This state indicates that the cell previously contained an active pair (key, value), but it was deleted, and the new active pair has not yet been recorded in the cell.
In the same way as in the “unused” state, after inserting the key, the cell from the “empty” state changes to the “active” state.
The “empty” cell cannot return to the “unused” state, that is, return me_key = NULL, since in this case the sequence of samples in the event of a collision will not be able to find out whether the cells were “active”.
ma_fill is the number of non-zero keys (me_key! = NULL), that is, the sum of “active” and “empty” cells.
ma_used is the number of non-zero and non-empty keys (me_key! = NULL, me_key! = dummy), that is, the number of "active" cells.
ma_mask - mask equal to PyDict_MINSIZE - 1.
ma_lookup - search function. By default, when creating a new dictionary, lookdict_string is used. This is done because the developers thought that most dictionaries contain only string keys.
The effectiveness of a hash table depends on the availability of “good” hash functions. A “good” hash function should be calculated quickly and with a minimum of collisions. But, unfortunately, the most frequently used and important hash functions (for string and integer types) return fairly regular values, which leads to collisions. Take an example:
For integers, hashes are their values, so the successive numbers will have consecutive hashes, and for rows, the successive lines have almost successive hashes. This is not necessarily bad, on the contrary, in a table of 2 ** i size, taking i low hash bits as the initial index of the table is very fast, and there will be no collisions for dictionaries indexed by a sequence of integers:

The same will be almost completely observed if the dictionary keys are “consecutive” lines (as in the example above). In general cases, this gives more than random behavior, which is what is required.

Taking only i low hash bits as an index is also vulnerable to collisions: for example, take the list [i << 16 for i in range (20000)] as a set of keys. Since the integers are their own hashes and this fits into a dictionary of size 2 ** 15 (since 20000 <32768), the last 15 bits from each hash will all be 0.
It turns out that all keys will have the same index. That is, for all keys (except the first one) collisions will occur.
Examples of specially selected "bad" cases should not affect ordinary cases, so just leave the last i bits taken. Everything else is at the mercy of the collision resolution method.
The procedure for selecting the appropriate cell to insert an element into a hash table is called probing, and the candidate cell in question is a sample.
Usually, the cell is located on the first attempt (and this is true, because the fill factor of the hash table is below 2/3), which allows not to waste time on probing and makes the calculation of the initial index very fast. But let's consider what happens if a collision occurs.
The first part of the collision resolution method is to calculate the indexes of the table for probing using the formula:
For any initial j within [0 .. (2 ** i - 1)], calling this formula 2 ** i will return each number within [0 .. (2 ** i - 1)] exactly once. For example:
You will say that this is no better than using linear probing with a constant step, because in this case, the cells in the hash table are also viewed in a certain order, but this is not the only difference. In general cases, when the hash of key values goes in a row, this method is better than linear probing. From the example above, we can see that for a table of size 8 (2 ** 3) the order of the indices will be as follows:
If a collision occurs for a sample with an index of 5, then the next sample index will be 2, not 6, as in the case of linear probing with a step of +1, therefore for a key added in the future, the sample index of which will be equal to 6, there will be no collision . Linear probing in this case (with consecutive key values) would be a bad option, since many collisions would occur. The probability that the hash of the keys will go in the order of 5 * j + 1 is much less.
The second part of the collision resolution method is to use not only the lower i bits of the hash, but the rest of the bits too. This is implemented using the perturb variable as follows:
After that, the sequence of samples will depend on each bit of hash. A pseudo-random change is very effective because it quickly increases bit differences. Since the perturb variable is unsigned, if probing is performed often enough, the perturb variable eventually becomes and remains zero. At this moment (which is very rarely achieved), the result j again becomes equal to 5 * j + 1. Next, the search is performed in the same way as in the first part of the method, and the free cell will eventually be found, because, as was said earlier, each a number in the range [0 .. (2 ** i - 1)] will be returned exactly once, and we are sure that there is always at least one “unused” cell.
Choosing a “good” value for PERTURB_SHIFT is a matter of balancing. If you make it small, the high-order bits of the hash will affect the sample sequence in iterations. If you make it big, then in really “bad” cases, the high-order bits of the hash will only affect early iterations. As a result of the experiments that were conducted by one of the Python developers, Tim Peters, the PERTURB_SHIFT value was chosen equal to 5, since this value turned out to be “the best”. That is, it showed the minimum total number of collisions for both normal and specially selected "bad" cases, although the values 4 and 6 were not significantly worse.
Historical note: One of the Python developers, Reimer Berends, proposed the idea of using a polynomial-based index calculation approach, which was then improved by Christian Tismer. This approach also showed excellent results on the occurrence of collisions, but required more operations, as well as an additional variable for storing the table polynomial in the PyDictObject structure. In Tim Peters' experiments, the current method used in Python turned out to be faster, showing equally good results for collisions, but required less code and used less memory.
When you create a dictionary, the PyDict_New function is called. In this function, the following operations are performed sequentially: memory is allocated for a new PyDictObject dictionary object. The variable ma_smalltable is cleared. The variables ma_used and ma_fill are equal to 0, ma_table becomes equal to ma_smalltable. The ma_mask value is equal to PyDict_MINSIZE - 1. The ma_lookup search function is set to lookdict_string. The created dictionary object is returned.
When adding an item to the dictionary or changing the value of an item in the dictionary, the PyDict_SetItem function is called. In this function, the hash value is taken and the insertdict function is called, as well as the dictresize function, if the table is 2/3 full of the current size.
In turn, the function insertdict calls the lookdict_string (or lookdict, if the dictionary has a non-string key), in which a free cell is searched in the hash table for insertion. The same function is used to find the key when extracting.
The initial sample index in this function is calculated as a hash of the key divided by the module by the size of the table (thus, the lower bits of the hash are taken). I.e:
In Python, this is implemented using a logical AND operation and a mask. The mask is equal to the following value: mask = PyDict_MINSIZE - 1.
This is how the lower bits of the hash are obtained:
2 ** i = PyDict_MINSIZE, hence i = 3, that is, three low bits are enough.
hash (123) = 123 = 1111011 2
mask = PyDict_MINSIZE - 1 = 8 - 1 = 7 = 111 2
index = hash (123) & mask = 1111 011 2 & 111 2 = 011 2 = 3
After the index is calculated, the cell is checked by its index, and if it is “unused”, then an entry is added to it (hash, key, value). But if this cell is busy, because the other entry has the same hash (that is, a collision has occurred), the hash and key of the inserted entry and the entry in the cell are compared. If the hash and the key for the entries match, then it is considered that the entry already exists in the dictionary, and it is updated.
This explains the tricky moment associated with the addition of equal in value but different in type keys (for example, float, int and complex):
That is, the type that was added to the dictionary first, and will be the type of key, despite the update. This is because the implementation of the hash for float values returns a hash of an int if the fractional part is 0.0. An example of a hash calculation for float rewritten in Python:
And the hash from the complex returns the hash from the float. In this case, only the real part hash is returned, since the imaginary part is zero:
Example:
Since both the hashes and the values for all three types are equal, a simple update of the value of the found record is performed.
Note about adding items: Python prohibits adding items to the dictionary during iteration, so when you try to add a new item, an error occurs:
Let's return to the procedure of adding an element to the dictionary. After successfully adding or updating a record in the hash table, the next candidate entry is compared. If the hash or key of the records do not match, probing begins. A search for an “unused” cell for insertion. In this Python implementation, random (and if perturb variable is zero - quadratic) probing is used. As described above, when randomly probing, the index of the next cell is selected in a pseudo-random manner. The entry is added to the first “unused” cell found. That is, two keys a and b, in which hash (a) == hash (b), but a! = B can easily exist in one dictionary. If the cell according to the initial sample index is “empty”, probing will occur. And if the first cell found is “zero”, then the “empty” cell will be used again. This allows you to overwrite deleted cells, while still saving unused ones.
It turns out that the indexes of the elements added to the dictionary depend on the elements already in it, and the order of the keys for two dictionaries consisting of the same set of pairs (key, value) may be different and is determined by the order of adding elements:
This explains why dictionaries in Python display stored pairs (key, value) in the order in which they are added to the dictionary when displaying content. Dictionaries output them in order of location in the hash table (that is, in the order of the indices).
Consider an example:
Insertion occurred at index 5. The variables ma_fill and ma_used have become equal to 1.
Insertion occurred at index 0. The variables ma_fill and ma_used have become equal to 2.
Insertion occurred at index 4. The ma_fill and ma_used variables are equal to 3.
Insertion has occurred at index 1. The variables ma_fill and ma_used have become equal to 4.
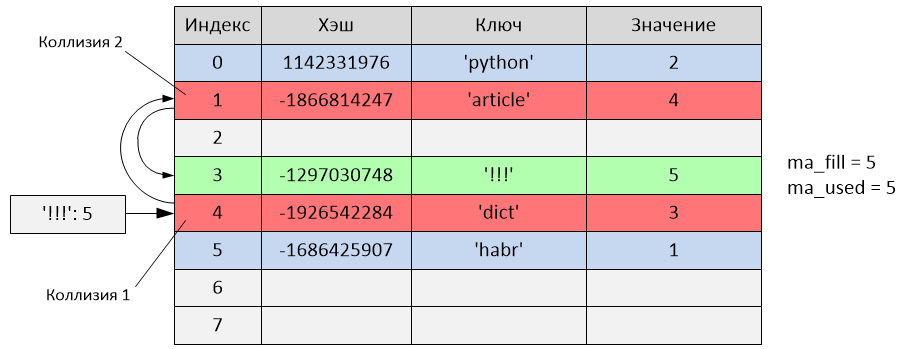
The following happened:
hash ('!!!') = -1297030748
i = -1297030748 & 7 = 4
But as can be seen from the table, index 4 is already occupied by writing with the 'dict' key. That is, a collision occurred. Testing begins:
perturb = -1297030748
i = (i * 5) + 1 + perturb
i = (4 * 5) + 1 + (-1297030748) = -1297030727
index = -1297030727 & 7 = 1
The new sample index is 1, but this index is also occupied (with the 'article' key). Another collision has occurred, we continue probing:
perturb = perturb >> PERTURB_SHIFT
perturb = -1297030748 >> 5 = -40532211
i = (i * 5) + 1 + perturb
i = (-1297030727 * 5) + 1 + (-40532211) = -6525685845
index = -6525685845 & 7 = 3
The new sample index is 3, and since it is not busy, an entry is inserted with the key '!!!' in the cell with the third index. In this case, the record was added after two trials due to collisions. The variables ma_fill and ma_used have become equal to 5.
We try to add the sixth element to the dictionary.
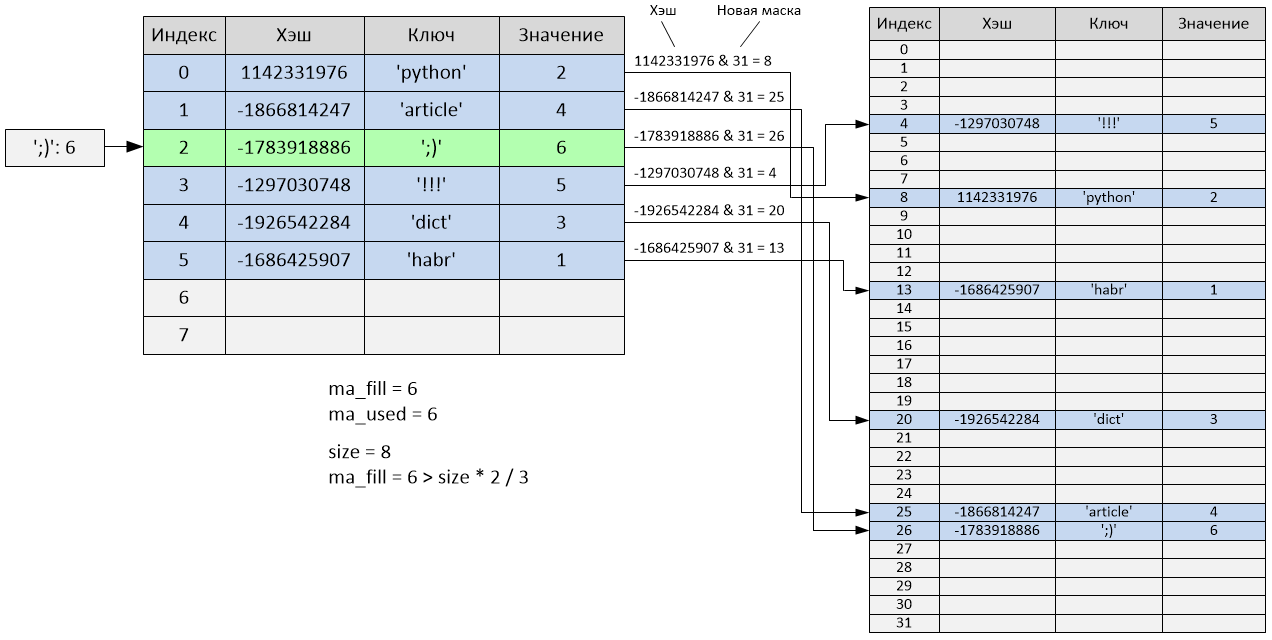
After adding the sixth element, the table will be filled to 2/3, and accordingly, its size will change. After the size changes (in this case it will increase by 4 times), the hash table will be completely rebuilt to take into account the new size - all “active” cells will be redistributed, and “empty” and “unused” cells will be ignored.
The size of the hash table is now 32, and the variables ma_fill and ma_used are equal to 6. As you can see, the order of the elements has completely changed:
The search for an entry in the dictionary hash table is similar, starting with cell i, where i depends on the key hash. ( ) – , , , . , , .
, 2/3. - , 8, , 6 .
In this case, the hash table is rebuilt with regard to its new size, and, accordingly, the indexes of all records change.
A value of 2/3 of the size was chosen as optimal in order for probing not to take too much time, that is, the insertion of a new record occurred quickly. Increasing this value leads to the fact that the dictionary is more densely filled with entries, which in turn increases the number of collisions. The decrease also increases the sparseness of the records to the detriment of the increase in the cache lines of the processor they occupy and to the detriment of the increase in the total amount of memory. The check of the table is filled in a very time sensitive part of the code. Attempts to make the check more complex (for example, changing the fill factor for different sizes of the hash table) reduced performance.
, , :
PyDictObject 64- .
8. , 6 ( 2/3 ), 32. , 22, 128. 86 512, 342 – 2048 .
The increase in the size of the table when the maximum fill level is reached is 4 if the size of the table is less than 50,000 elements, and 2 for larger tables. This approach may be useful for applications with memory limitations.
Increasing the size of the table improves the average sparseness, that is, the spread of entries in the dictionary table (reducing collisions), by increasing the amount of memory consumed and the speed of iterations, and also reduces the number of expensive memory allocation operations when resizing for a growing dictionary.
Usually adding an item to a dictionary can increase its size 4 or 2 times depending on the current size of the dictionary, but it is also possible that the size of the dictionary will decrease. Such a situation can occur if ma_fill (the number of non-zero keys, the sum of “active” and “empty” cells) is much more than ma_used (the number of “active” cells), that is, many keys have been deleted.
When an item is removed from the dictionary, the PyDict_DelItem function is called.
Deletion from the dictionary occurs by key, although in reality the memory is not freed. In this function, the hash value of the key is calculated, and then a record is searched in the hash table using the same lookdict_string or lookdict function. If an entry with such a key and a hash is found, the key of this entry is set to “empty” (that is, me_key = dummy), and the value of the entry is set to NULL (me_value = NULL). After that, the variable ma_used will decrease by one, and ma_fill will remain unchanged. If the record is not found, an error is returned.
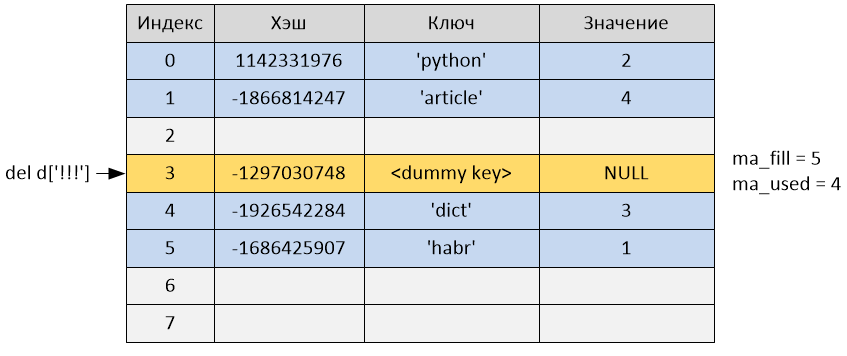
After deletion, the ma_used variable became equal to 4, and ma_fill remained equal to 5, since the cell was not deleted, but was only marked as “empty” and continues to occupy the cell in the hash table.
When running python, you can use the -R switch to use a pseudo-random salt. In this case, the hash values of such types as strings, buffer, bytes, and datetime objects (date, time, and datetime) will be unpredictable between interpreter calls. This method is proposed as a defense against DoS attacks.
github.com/python/cpython/blob/2.7/Objects/dictobject.c
github.com/python/cpython/blob/2.7/Include/dictobject.h
github.com/python/cpython/blob/2.7/Objects/dictnotes.txt
www.shutupandship.com/2012/02/how-hash-collisions-are-resolved-in.html
www.laurentluce.com/posts/python-dictionary-implementation
rhodesmill.org/brandon/slides/2010-03-pycon
www.slideshare.net/MinskPythonMeetup/ss-26224561 – Dictionary Python. Objects/dictnotes.txt – SlideShare (Cyril notorca Lashkevich)
www.youtube.com/watch?v=JhixzgVpmdM – «Dictionary Python. Objects/dictnotes.txt»
To write this article I pushed a question on the Stack Overflow.
The article discusses the implementation of CPython version 2.7. All examples were prepared in the 32-bit version of Python on a 64-bit OS, for another version the values will be different.
Python dictionary
A dictionary in Python is an associative array, that is, it stores data in the form of pairs (key, value). A dictionary is a variable data type. This means that you can add elements to it, change them and delete them from the dictionary. It also provides the operation of finding and returning an item by key.
Initializing and adding elements:
')
>>> d = {} # , d = dict() >>> d['a'] = 123 >>> d['b'] = 345 >>> d['c'] = 678 >>> d {'a': 123, 'c': 678, 'b': 345} Item receipt:
>>> d['b'] 345 Deleting an item:
>>> del d['c'] >>> d {'a': 123, 'b': 345} The keys of the dictionary can be values of only hashable types, that is, types that can have a hash (for this they must have __hash __ () method). Therefore, values of such types as a list (list), a set (set) and the dictionary itself (dict) cannot be keys of a dictionary:
>>> d[list()] = 1 Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: unhashable type: 'list' >>> d[set()] = 2 Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: unhashable type: 'set' >>> d[dict()] = 3 Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: unhashable type: 'dict' Implementation
The Python dictionary is implemented as a hash table. As is known, the implementation of a hash table should take into account the possibility of collisions - situations where different keys have the same hash value. There should be a way to insert and extract elements with regard to collisions. There are several ways to resolve collisions, such as the chaining method and the open addressing method. Python uses an open addressing method. The developers preferred the open addressing method to the chaining method due to the fact that it can significantly save memory on storing pointers that are used in hash tables with chains.
In the implementation under consideration, each entry (PyDictEntry) in the hash table of the dictionary consists of three elements — a hash, a key, and a value.
typedef struct { Py_ssize_t me_hash; PyObject *me_key; PyObject *me_value; } PyDictEntry; The structure of PyDictObject is as follows:
#define PyDict_MINSIZE 8 typedef struct _dictobject PyDictObject; struct _dictobject { PyObject_HEAD Py_ssize_t ma_fill; Py_ssize_t ma_used; Py_ssize_t ma_mask; PyDictEntry *ma_table; PyDictEntry *(*ma_lookup)(PyDictObject *mp, PyObject *key, long hash); PyDictEntry ma_smalltable[PyDict_MINSIZE]; }; When creating a new dictionary object, its size is 8. This value is determined by the constant PyDict_MINSIZE. To store a hash table, the variables ma_smalltable and ma_table have been entered into PyDictObject. The pre-allocated ma_smalltable variable, PyDict_MINSIZE (that is, 8), allows small dictionaries (up to 8 PyDictEntry objects) to be stored without additional memory allocation. Experiments conducted by developers have shown that this size is quite enough for most dictionaries: small dictionaries of instances and usually small dictionaries created for passing named arguments (kwargs). The variable ma_table corresponds to ma_smalltable for small tables (that is, for tables of 8 cells). For larger tables, ma_table memory is allocated separately. The variable ma_table cannot be NULL.
If someone suddenly wants to change the value of PyDict_MINSIZE, it can be done in the source, and then rebuild Python. The value is recommended to be equal to the power of two, but not less than four.
A cell in a hash table can have three states.
1) Unused (me_key == me_value == NULL)
This state means that the cell does not contain and has never yet contained a pair (key, value).
After the key is inserted, the “unused” cell changes to the “active” state.
This state is the only case when me_key = NULL and is the initial state for all cells in the table.
2) Active (me_key! = NULL and me_key! = Dummy and me_value! = NULL)
Indicates that the cell contains an active pair (key, value).
After the key is removed, the cell from the “active” state changes to the “empty” state (that is, me_key = dummy,
dummy = PyString_FromString ("<dummy key>")).
This is the only state when me_value! = NULL.
3) Empty (me_key == dummy and me_value == NULL)
This state indicates that the cell previously contained an active pair (key, value), but it was deleted, and the new active pair has not yet been recorded in the cell.
In the same way as in the “unused” state, after inserting the key, the cell from the “empty” state changes to the “active” state.
The “empty” cell cannot return to the “unused” state, that is, return me_key = NULL, since in this case the sequence of samples in the event of a collision will not be able to find out whether the cells were “active”.
Member variables
ma_fill is the number of non-zero keys (me_key! = NULL), that is, the sum of “active” and “empty” cells.
ma_used is the number of non-zero and non-empty keys (me_key! = NULL, me_key! = dummy), that is, the number of "active" cells.
ma_mask - mask equal to PyDict_MINSIZE - 1.
ma_lookup - search function. By default, when creating a new dictionary, lookdict_string is used. This is done because the developers thought that most dictionaries contain only string keys.
Main details
The effectiveness of a hash table depends on the availability of “good” hash functions. A “good” hash function should be calculated quickly and with a minimum of collisions. But, unfortunately, the most frequently used and important hash functions (for string and integer types) return fairly regular values, which leads to collisions. Take an example:
>>> map(hash, [0, 1, 2, 3, 4]) [0, 1, 2, 3, 4] >>> map(hash, ['abca', 'abcb', 'abcc', 'abcd', 'abce']) [1540938117, 1540938118, 1540938119, 1540938112, 1540938113] For integers, hashes are their values, so the successive numbers will have consecutive hashes, and for rows, the successive lines have almost successive hashes. This is not necessarily bad, on the contrary, in a table of 2 ** i size, taking i low hash bits as the initial index of the table is very fast, and there will be no collisions for dictionaries indexed by a sequence of integers:

The same will be almost completely observed if the dictionary keys are “consecutive” lines (as in the example above). In general cases, this gives more than random behavior, which is what is required.

Taking only i low hash bits as an index is also vulnerable to collisions: for example, take the list [i << 16 for i in range (20000)] as a set of keys. Since the integers are their own hashes and this fits into a dictionary of size 2 ** 15 (since 20000 <32768), the last 15 bits from each hash will all be 0.
>>> map(lambda x: '{0:016b}'.format(x), [i << 16 for i in xrange(20000)]) ['0000000000000000', '10000000000000000', '100000000000000000', '110000000000000000', '1000000000000000000', '1010000000000000000', '1100000000000000000', '1110000000000000000', ...] It turns out that all keys will have the same index. That is, for all keys (except the first one) collisions will occur.
Examples of specially selected "bad" cases should not affect ordinary cases, so just leave the last i bits taken. Everything else is at the mercy of the collision resolution method.
Collision resolution method
The procedure for selecting the appropriate cell to insert an element into a hash table is called probing, and the candidate cell in question is a sample.
Usually, the cell is located on the first attempt (and this is true, because the fill factor of the hash table is below 2/3), which allows not to waste time on probing and makes the calculation of the initial index very fast. But let's consider what happens if a collision occurs.
The first part of the collision resolution method is to calculate the indexes of the table for probing using the formula:
j = ((5 * j) + 1) % 2**i For any initial j within [0 .. (2 ** i - 1)], calling this formula 2 ** i will return each number within [0 .. (2 ** i - 1)] exactly once. For example:
>>> j = 0 >>> i = 3 >>> for _ in xrange(0, 2**i): ... print j, ... j = ((5 * j) + 1) % 2**i ... 0 1 6 7 4 5 2 3 You will say that this is no better than using linear probing with a constant step, because in this case, the cells in the hash table are also viewed in a certain order, but this is not the only difference. In general cases, when the hash of key values goes in a row, this method is better than linear probing. From the example above, we can see that for a table of size 8 (2 ** 3) the order of the indices will be as follows:
0 -> 1 -> 6 -> 7 -> 4 -> 5 -> 2 -> 3 -> 0 -> … ( ) If a collision occurs for a sample with an index of 5, then the next sample index will be 2, not 6, as in the case of linear probing with a step of +1, therefore for a key added in the future, the sample index of which will be equal to 6, there will be no collision . Linear probing in this case (with consecutive key values) would be a bad option, since many collisions would occur. The probability that the hash of the keys will go in the order of 5 * j + 1 is much less.
The second part of the collision resolution method is to use not only the lower i bits of the hash, but the rest of the bits too. This is implemented using the perturb variable as follows:
j = (5 * j) + 1 + perturb perturb >>= PERTURB_SHIFT j % 2**i : perturb = hash(key) PERTURB_SHIFT = 5 After that, the sequence of samples will depend on each bit of hash. A pseudo-random change is very effective because it quickly increases bit differences. Since the perturb variable is unsigned, if probing is performed often enough, the perturb variable eventually becomes and remains zero. At this moment (which is very rarely achieved), the result j again becomes equal to 5 * j + 1. Next, the search is performed in the same way as in the first part of the method, and the free cell will eventually be found, because, as was said earlier, each a number in the range [0 .. (2 ** i - 1)] will be returned exactly once, and we are sure that there is always at least one “unused” cell.
Choosing a “good” value for PERTURB_SHIFT is a matter of balancing. If you make it small, the high-order bits of the hash will affect the sample sequence in iterations. If you make it big, then in really “bad” cases, the high-order bits of the hash will only affect early iterations. As a result of the experiments that were conducted by one of the Python developers, Tim Peters, the PERTURB_SHIFT value was chosen equal to 5, since this value turned out to be “the best”. That is, it showed the minimum total number of collisions for both normal and specially selected "bad" cases, although the values 4 and 6 were not significantly worse.
Historical note: One of the Python developers, Reimer Berends, proposed the idea of using a polynomial-based index calculation approach, which was then improved by Christian Tismer. This approach also showed excellent results on the occurrence of collisions, but required more operations, as well as an additional variable for storing the table polynomial in the PyDictObject structure. In Tim Peters' experiments, the current method used in Python turned out to be faster, showing equally good results for collisions, but required less code and used less memory.
Dictionary initialization
When you create a dictionary, the PyDict_New function is called. In this function, the following operations are performed sequentially: memory is allocated for a new PyDictObject dictionary object. The variable ma_smalltable is cleared. The variables ma_used and ma_fill are equal to 0, ma_table becomes equal to ma_smalltable. The ma_mask value is equal to PyDict_MINSIZE - 1. The ma_lookup search function is set to lookdict_string. The created dictionary object is returned.
Add item
When adding an item to the dictionary or changing the value of an item in the dictionary, the PyDict_SetItem function is called. In this function, the hash value is taken and the insertdict function is called, as well as the dictresize function, if the table is 2/3 full of the current size.
In turn, the function insertdict calls the lookdict_string (or lookdict, if the dictionary has a non-string key), in which a free cell is searched in the hash table for insertion. The same function is used to find the key when extracting.
The initial sample index in this function is calculated as a hash of the key divided by the module by the size of the table (thus, the lower bits of the hash are taken). I.e:
>>> PyDict_MINSIZE = 8 >>> key = 123 >>> hash(key) % PyDict_MINSIZE >>> 3 In Python, this is implemented using a logical AND operation and a mask. The mask is equal to the following value: mask = PyDict_MINSIZE - 1.
>>> PyDict_MINSIZE = 8 >>> mask = PyDict_MINSIZE - 1 >>> key = 123 >>> hash(key) & mask >>> 3 This is how the lower bits of the hash are obtained:
2 ** i = PyDict_MINSIZE, hence i = 3, that is, three low bits are enough.
hash (123) = 123 = 1111011 2
mask = PyDict_MINSIZE - 1 = 8 - 1 = 7 = 111 2
index = hash (123) & mask = 1111 011 2 & 111 2 = 011 2 = 3
After the index is calculated, the cell is checked by its index, and if it is “unused”, then an entry is added to it (hash, key, value). But if this cell is busy, because the other entry has the same hash (that is, a collision has occurred), the hash and key of the inserted entry and the entry in the cell are compared. If the hash and the key for the entries match, then it is considered that the entry already exists in the dictionary, and it is updated.
This explains the tricky moment associated with the addition of equal in value but different in type keys (for example, float, int and complex):
>>> 7.0 == 7 == (7+0j) True >>> d = {} >>> d[7.0]='float' >>> d {7.0: 'float'} >>> d[7]='int' >>> d {7.0: 'int'} >>> d[7+0j]='complex' >>> d {7.0: 'complex'} >>> type(d.keys()[0]) <type 'float'> That is, the type that was added to the dictionary first, and will be the type of key, despite the update. This is because the implementation of the hash for float values returns a hash of an int if the fractional part is 0.0. An example of a hash calculation for float rewritten in Python:
def float_hash(float_value): ... fractpart, intpart = math.modf(float_value) if fractpart == 0.0: return int_hash(int(float_value)) # int ... And the hash from the complex returns the hash from the float. In this case, only the real part hash is returned, since the imaginary part is zero:
def complex_hash(complex_value): hashreal = float_hash(complex_value.real) if hashreal == -1: return -1 hashimag = float_hash(complex_value.imag) if hashimag == -1: return -1 res = hashreal + 1000003 * hashimag res = handle_overflow(res) if res == -1: res = -2 return res Example:
>>> hash(7) 7 >>> hash(7.0) 7 >>> hash(7+0j) 7 Since both the hashes and the values for all three types are equal, a simple update of the value of the found record is performed.
Note about adding items: Python prohibits adding items to the dictionary during iteration, so when you try to add a new item, an error occurs:
>>> d = {'a': 1} >>> for i in d: ... d['new item'] = 123 ... Traceback (most recent call last): File "<stdin>", line 1, in <module> RuntimeError: dictionary changed size during iteration Let's return to the procedure of adding an element to the dictionary. After successfully adding or updating a record in the hash table, the next candidate entry is compared. If the hash or key of the records do not match, probing begins. A search for an “unused” cell for insertion. In this Python implementation, random (and if perturb variable is zero - quadratic) probing is used. As described above, when randomly probing, the index of the next cell is selected in a pseudo-random manner. The entry is added to the first “unused” cell found. That is, two keys a and b, in which hash (a) == hash (b), but a! = B can easily exist in one dictionary. If the cell according to the initial sample index is “empty”, probing will occur. And if the first cell found is “zero”, then the “empty” cell will be used again. This allows you to overwrite deleted cells, while still saving unused ones.
It turns out that the indexes of the elements added to the dictionary depend on the elements already in it, and the order of the keys for two dictionaries consisting of the same set of pairs (key, value) may be different and is determined by the order of adding elements:
>>> d1 = {'one': 1, 'two': 2, 'three': 3, 'four': 4, 'five': 5} >>> d2 = {'three': 3, 'two': 2, 'five': 5, 'four': 4, 'one': 1} >>> d1 == d2 True >>> d1.keys() ['four', 'three', 'five', 'two', 'one'] >>> d2.keys() ['four', 'one', 'five', 'three', 'two'] This explains why dictionaries in Python display stored pairs (key, value) in the order in which they are added to the dictionary when displaying content. Dictionaries output them in order of location in the hash table (that is, in the order of the indices).
Consider an example:
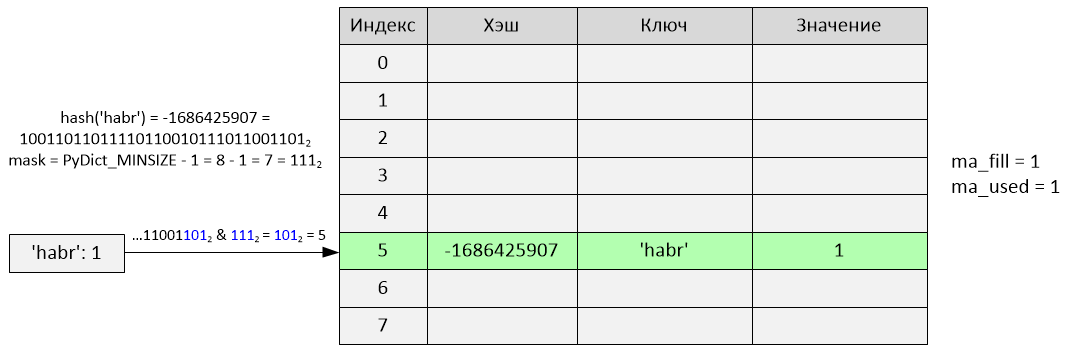
>>> d = {} >>> d['habr'] = 1 
Insertion occurred at index 5. The variables ma_fill and ma_used have become equal to 1.
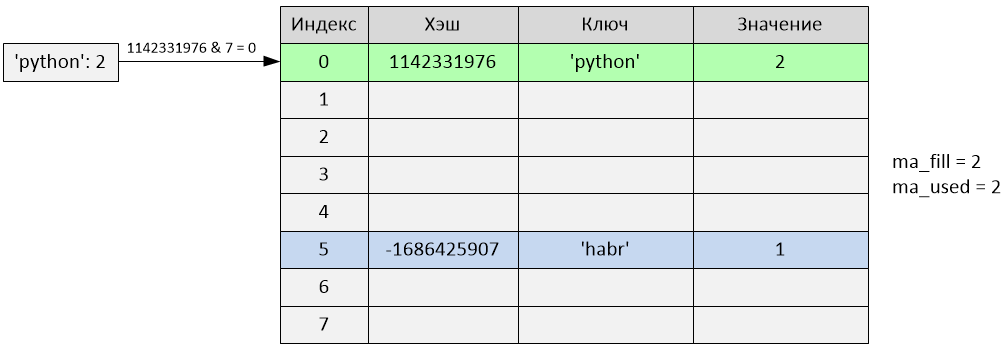
>>> d['python'] = 2 
Insertion occurred at index 0. The variables ma_fill and ma_used have become equal to 2.
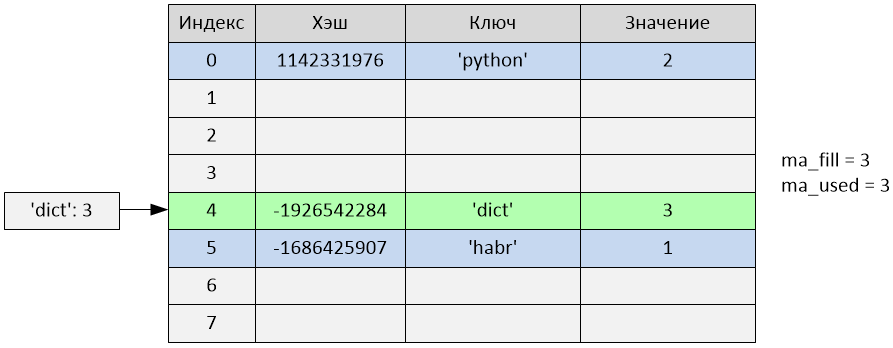
>>> d['dict'] = 3 
Insertion occurred at index 4. The ma_fill and ma_used variables are equal to 3.
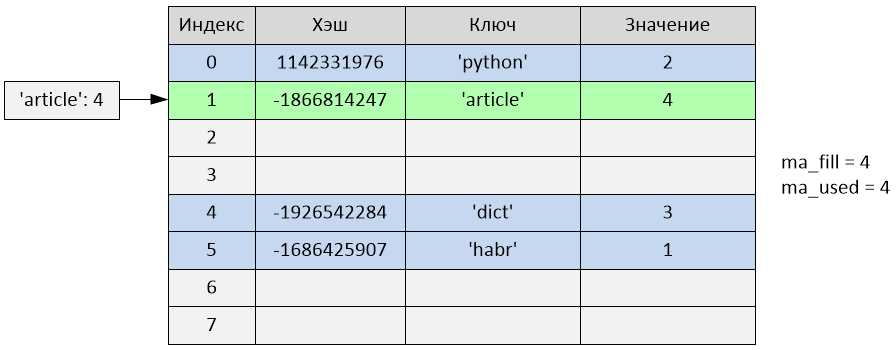
>>> d['article'] = 4 
Insertion has occurred at index 1. The variables ma_fill and ma_used have become equal to 4.
>>> d['!!!'] = 5 
The following happened:
hash ('!!!') = -1297030748
i = -1297030748 & 7 = 4
But as can be seen from the table, index 4 is already occupied by writing with the 'dict' key. That is, a collision occurred. Testing begins:
perturb = -1297030748
i = (i * 5) + 1 + perturb
i = (4 * 5) + 1 + (-1297030748) = -1297030727
index = -1297030727 & 7 = 1
The new sample index is 1, but this index is also occupied (with the 'article' key). Another collision has occurred, we continue probing:
perturb = perturb >> PERTURB_SHIFT
perturb = -1297030748 >> 5 = -40532211
i = (i * 5) + 1 + perturb
i = (-1297030727 * 5) + 1 + (-40532211) = -6525685845
index = -6525685845 & 7 = 3
The new sample index is 3, and since it is not busy, an entry is inserted with the key '!!!' in the cell with the third index. In this case, the record was added after two trials due to collisions. The variables ma_fill and ma_used have become equal to 5.
>>> d {'python': 2, 'article': 4, '!!!': 5, 'dict': 3, 'habr': 1} We try to add the sixth element to the dictionary.
>>> d[';)'] = 6 
After adding the sixth element, the table will be filled to 2/3, and accordingly, its size will change. After the size changes (in this case it will increase by 4 times), the hash table will be completely rebuilt to take into account the new size - all “active” cells will be redistributed, and “empty” and “unused” cells will be ignored.
The size of the hash table is now 32, and the variables ma_fill and ma_used are equal to 6. As you can see, the order of the elements has completely changed:
>>> d {'!!!': 5, 'python': 2, 'habr': 1, 'dict': 3, 'article': 4, ';)': 6} Item Search
The search for an entry in the dictionary hash table is similar, starting with cell i, where i depends on the key hash. ( ) – , , , . , , .
>>> d = {'a': 123, 'b': 345, 'c': 678} >>> d['x'] Traceback (most recent call last): File "<stdin>", line 1, in <module> KeyError: 'x' -
, 2/3. - , 8, , 6 .
>>> 8 * 2.0 / 3 5.333333333333333 In this case, the hash table is rebuilt with regard to its new size, and, accordingly, the indexes of all records change.
A value of 2/3 of the size was chosen as optimal in order for probing not to take too much time, that is, the insertion of a new record occurred quickly. Increasing this value leads to the fact that the dictionary is more densely filled with entries, which in turn increases the number of collisions. The decrease also increases the sparseness of the records to the detriment of the increase in the cache lines of the processor they occupy and to the detriment of the increase in the total amount of memory. The check of the table is filled in a very time sensitive part of the code. Attempts to make the check more complex (for example, changing the fill factor for different sizes of the hash table) reduced performance.
, , :
>>> d = dict.fromkeys(range(5)) >>> d.__sizeof__() 248 >>> d = dict.fromkeys(range(6)) >>> d.__sizeof__() 1016 PyDictObject 64- .
8. , 6 ( 2/3 ), 32. , 22, 128. 86 512, 342 – 2048 .
The increase in the size of the table when the maximum fill level is reached is 4 if the size of the table is less than 50,000 elements, and 2 for larger tables. This approach may be useful for applications with memory limitations.
Increasing the size of the table improves the average sparseness, that is, the spread of entries in the dictionary table (reducing collisions), by increasing the amount of memory consumed and the speed of iterations, and also reduces the number of expensive memory allocation operations when resizing for a growing dictionary.
Usually adding an item to a dictionary can increase its size 4 or 2 times depending on the current size of the dictionary, but it is also possible that the size of the dictionary will decrease. Such a situation can occur if ma_fill (the number of non-zero keys, the sum of “active” and “empty” cells) is much more than ma_used (the number of “active” cells), that is, many keys have been deleted.
Remove item
When an item is removed from the dictionary, the PyDict_DelItem function is called.
Deletion from the dictionary occurs by key, although in reality the memory is not freed. In this function, the hash value of the key is calculated, and then a record is searched in the hash table using the same lookdict_string or lookdict function. If an entry with such a key and a hash is found, the key of this entry is set to “empty” (that is, me_key = dummy), and the value of the entry is set to NULL (me_value = NULL). After that, the variable ma_used will decrease by one, and ma_fill will remain unchanged. If the record is not found, an error is returned.
>>> del d['!!!'] 
After deletion, the ma_used variable became equal to 4, and ma_fill remained equal to 5, since the cell was not deleted, but was only marked as “empty” and continues to occupy the cell in the hash table.
Randomization hashes
When running python, you can use the -R switch to use a pseudo-random salt. In this case, the hash values of such types as strings, buffer, bytes, and datetime objects (date, time, and datetime) will be unpredictable between interpreter calls. This method is proposed as a defense against DoS attacks.
Links
github.com/python/cpython/blob/2.7/Objects/dictobject.c
github.com/python/cpython/blob/2.7/Include/dictobject.h
github.com/python/cpython/blob/2.7/Objects/dictnotes.txt
www.shutupandship.com/2012/02/how-hash-collisions-are-resolved-in.html
www.laurentluce.com/posts/python-dictionary-implementation
rhodesmill.org/brandon/slides/2010-03-pycon
www.slideshare.net/MinskPythonMeetup/ss-26224561 – Dictionary Python. Objects/dictnotes.txt – SlideShare (Cyril notorca Lashkevich)
www.youtube.com/watch?v=JhixzgVpmdM – «Dictionary Python. Objects/dictnotes.txt»
Source: https://habr.com/ru/post/247843/
All Articles