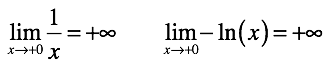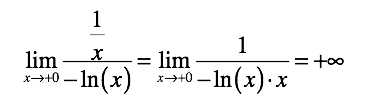Divide by zero is the norm. Part 1
Part 1. Actually, everyone has already divided everything up to us!
Part 2. Truth is somewhere nearby
They say it can be divided by zero if you determine the result of division by zero. Just need to expand algebra. By a strange coincidence, to find at least some, and better understandable and simple, an example of such an extension fails. To fix the Internet you need either a demonstration of one of the ways of such an extension, or a description of why this is not possible.

The article is written in continuation of the trend:
The purpose of this article is to explain in "human language" how the fundamental foundations of mathematics work, to structure knowledge and to restore the lost cause-and-effect relationships between the branches of mathematics. All arguments are philosophical, in part of the judgments are at odds with generally accepted ones (therefore, they do not pretend to mathematical rigor). The article is designed for the reader level "passed the tower many years ago."
')
Understanding the principles of arithmetic, elementary, general and linear algebra, mathematical and non-standard analysis, set theory, general topology, projective and affine geometry is desirable, but not necessary.
During the experiments, no infinity suffered.
Going beyond the box is a natural process of finding new knowledge. But not every search brings new knowledge and therefore benefits.
To begin with, from what begin, probably, all adventurers when dividing by zero. Recall the function graph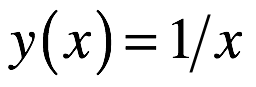 .
.

To the left and to the right of zero, the function goes in different directions of “non-existence”. In the very zero, “pool” and nothing is visible.
Instead of rushing into the "pool" with your head, let's see what flows in and out of there. To do this, we use the limit - the main tool for mathematical analysis . The main “trick” is that the limit allows you to go to a given point as close as possible, but not “step on it”. Such a "fence" before the "pool."
Original
Well, the "fence" set. Not so scary anymore. We have two paths to the pool. Let's go to the left - a steep descent, to the right - a steep climb. How many do not go to the "fence", it does not become closer. To cross the lower and upper "non-existence" does not go. There are suspicions, maybe we go in a circle? Although no, the numbers change, it means not in a circle. We rummage in the trunk with the tools of mathematical analysis yet. In addition to the limits with the "fence" in the kit, there is a positive and negative infinity . The values are completely abstract (they are not numbers), well formalized and ready to use! It suits us. Let us complement our "being" (the set of real numbers) with two infinities with a sign.

Mathematical language:
Walking through the schedule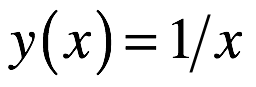 , we have only two ways to zero (left and right). At the end of each path is a small "fence." By a strange coincidence, the same "fence" was both at the bottom and at the top of "being." If we want the paths to converge, then behind the "fence" we need a teleport from one end of the "being" to the other. We have already seen such teleports. No problem.
, we have only two ways to zero (left and right). At the end of each path is a small "fence." By a strange coincidence, the same "fence" was both at the bottom and at the top of "being." If we want the paths to converge, then behind the "fence" we need a teleport from one end of the "being" to the other. We have already seen such teleports. No problem.

Let's try to connect both borders of "being" in the way our ancestors did. Let's go one dimension higher. Let's display a one-dimensional line on a two-dimensional plane.
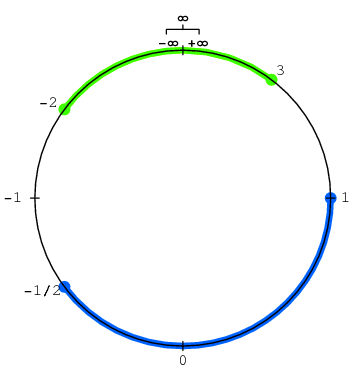
After docking, the presence of two sign infinities loses its meaning. Instead, you can enter one common intersection point, unsigned infinity.
This docking is very similar to the date reversal line located (mostly) between the UTC + 12 and UTC-12 time zones in the Pacific Ocean. It is there that teleport from today to yesterday and from today to tomorrow is located. We have the same teleport from ultra small to extra large.
Mathematical language:
Well, got rid of the minus sign. However, in zero, we have a second-type discontinuity and it cannot be considered a removable discontinuity point by definition. Violated the requirement of "limb" limit. Accordingly, we can not judge the equality of the limit on the right and left.
But since the approach to infinity is performed according to the same rules, we can say that the limits on the left and on the right coincide. Accordingly, we can take our discontinuity as a point of a removable discontinuity at infinity.
Mathematical language:
Well, the limits are the same. Now, it seems, everything is ready to bridge the gap between them.

In the mathematical model using the projective extension of the number line , the division by zero is defined.
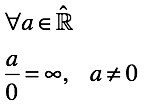
It seems that our problem is solved. However, we will not be in a hurry, let's see what the consequences are. In addition to the division, the following operations are defined in the system (recall that the infinity is unsigned).

Almost all of them with additional conditions, it is alarming. But let's not hurry, better look at the list of undefined operations:

Let's see how the distribution law will behave. Substitute in it certain values and perform the required operations.
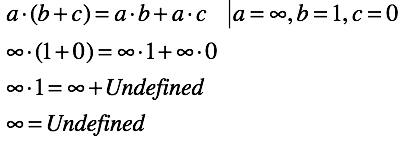
As a result, some of the identities cease to behave as we are used to. However, they did not disappear without a trace. The distribution law only works from right to left (i.e., in the case where the right-hand side of equality is defined). This is one of the clearest examples of negative consequences. Other identities are preserved in a more or less stable form.
Summing up:
The bottom line. Old approaches have stopped working. The complexity of the system, in the form of a heap “if”, “for all but”, etc., has increased. We had only two uncertainties 1/0 and 0/0 (we did not consider power operations), it became five. Disclosing one uncertainty gave rise to even more uncertainties.

On the introduction of unsigned infinity, everything did not stop. In order to get out of the uncertainties need a second wind.
So, we have a set of real numbers and two uncertainties 1/0 and 0/0. To eliminate the first, we performed a projective extension of the number line (that is, we entered unsigned infinity). Let's try to deal with the second uncertainty of the form 0/0. Let's do the same. Let's add the set of numbers with a new element representing the second uncertainty.

The definition of a division operation is based on multiplication. It does not suit us. Let's unbind operations from each other, but keep the usual behavior for real numbers. We define a unary division operation, denoted by the sign "/".
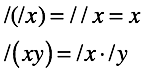
We will define operations.

This structure is called the “Wheel”. The term was taken because of the similarity with the topological picture of the projective extension of the numerical line and the point 0/0.

It seems everything looks good, but the devil is in the details:
In order to stabilize all the features, in addition to the expansion of the set of elements, a bonus is attached in the form of not one, but two identities describing distribution law.
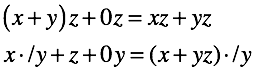
Mathematical language:
The world is no longer so beautiful, is it? Still, do not hurry. Check whether the new identities of the distribution law can cope with our extended set .
.
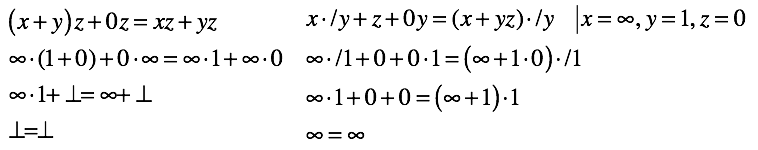
This time the result is much better.
Summing up:
The bottom line. Algebra works fine. However, the notion of “undefined” was taken as a basis, which was considered to be something existing and operate with it. One day someone will say that everything is bad and you need to break this “undefined” into several more “undefined”, but smaller. General algebra will say: “No problem, Bro!”.
Approximately the additional (j and k) imaginary units in quaternions are postulated like this.
It is worth noting that there are other algebraic systems with division. For example, "meadows" (common meadows). They are slightly simpler, since they do not expand the space by introducing new elements. The goal is achieved as in the wheels, the transformation of the operations of addition and multiplication, as well as the rejection of binary division.
The ability to "move the unknown" for mathematics is the norm. But all these wrappers do not give an answer to the main question, what is there inside?

Part 2. Truth is somewhere nearby
They say it can be divided by zero if you determine the result of division by zero. Just need to expand algebra. By a strange coincidence, to find at least some, and better understandable and simple, an example of such an extension fails. To fix the Internet you need either a demonstration of one of the ways of such an extension, or a description of why this is not possible.

The article is written in continuation of the trend:
Disclaimer
The purpose of this article is to explain in "human language" how the fundamental foundations of mathematics work, to structure knowledge and to restore the lost cause-and-effect relationships between the branches of mathematics. All arguments are philosophical, in part of the judgments are at odds with generally accepted ones (therefore, they do not pretend to mathematical rigor). The article is designed for the reader level "passed the tower many years ago."
')
Understanding the principles of arithmetic, elementary, general and linear algebra, mathematical and non-standard analysis, set theory, general topology, projective and affine geometry is desirable, but not necessary.
During the experiments, no infinity suffered.
Prologue
Going beyond the box is a natural process of finding new knowledge. But not every search brings new knowledge and therefore benefits.
1. Actually, everyone has already divided everything up to us!
1.1 Affine expansion of the number line
To begin with, from what begin, probably, all adventurers when dividing by zero. Recall the function graph

To the left and to the right of zero, the function goes in different directions of “non-existence”. In the very zero, “pool” and nothing is visible.
Instead of rushing into the "pool" with your head, let's see what flows in and out of there. To do this, we use the limit - the main tool for mathematical analysis . The main “trick” is that the limit allows you to go to a given point as close as possible, but not “step on it”. Such a "fence" before the "pool."

Original
Well, the "fence" set. Not so scary anymore. We have two paths to the pool. Let's go to the left - a steep descent, to the right - a steep climb. How many do not go to the "fence", it does not become closer. To cross the lower and upper "non-existence" does not go. There are suspicions, maybe we go in a circle? Although no, the numbers change, it means not in a circle. We rummage in the trunk with the tools of mathematical analysis yet. In addition to the limits with the "fence" in the kit, there is a positive and negative infinity . The values are completely abstract (they are not numbers), well formalized and ready to use! It suits us. Let us complement our "being" (the set of real numbers) with two infinities with a sign.
Mathematical language:
It is this extension that makes it possible to take the limit when the argument tends to infinity and to get infinity as a result of taking the limit.
There are two sections of mathematics that describe the same thing using different terminology.
From the geometrical point of view, an affine extension of the numerical straight line That is, the usual sequence of real numbers is “compressed” so that it is possible to operate with the boundaries of this sequence. Two abstract infinitely large quantities are introduced as boundaries (conditional). Expansion is affine , but this does not mean that it came from Greece, it means that the relative position of the points (in our case, numbers) on the line remains. From this it follows that the “more” and “less” relations are preserved, both for numbers between themselves and in comparison with boundaries.
From the point of view of the general topology , a two - point compactification of the number line was made by adding two idealized points (infinities with the opposite sign).
1.2 Projective extension of the number line
Walking through the schedule

Let's try to connect both borders of "being" in the way our ancestors did. Let's go one dimension higher. Let's display a one-dimensional line on a two-dimensional plane.

After docking, the presence of two sign infinities loses its meaning. Instead, you can enter one common intersection point, unsigned infinity.
This docking is very similar to the date reversal line located (mostly) between the UTC + 12 and UTC-12 time zones in the Pacific Ocean. It is there that teleport from today to yesterday and from today to tomorrow is located. We have the same teleport from ultra small to extra large.
Mathematical language:
In fact, this is an independent extension conducted over the initial set of real numbers. This extension is not based on the affine extension considered earlier.
From the geometrical point of view, the projective extension of the number line has been performed (there is information on wolfram.com ). That is, an idealized point is introduced that connects both ends of the real line. Since the expansion is not affine, the comparison of real numbers with infinity is not defined.
From the point of view of the general topology , a one - point compactification of the number line was made by adding an idealized point (unsigned infinity).
An analogous extension over the field of complex numbers is the Riemann Sphere, widely known in mathematical circles.
Well, got rid of the minus sign. However, in zero, we have a second-type discontinuity and it cannot be considered a removable discontinuity point by definition. Violated the requirement of "limb" limit. Accordingly, we can not judge the equality of the limit on the right and left.
But since the approach to infinity is performed according to the same rules, we can say that the limits on the left and on the right coincide. Accordingly, we can take our discontinuity as a point of a removable discontinuity at infinity.
Mathematical language:
Let's take a closer look at how we operate with infinitely large and small quantities. In operations, we often neglect the smallest ones of the lowest order simply by discarding them when recording the result.
Similar situation when finding derivatives
Discarding the "small things" we lose information! This is clearly seen in the example of taking limits. Consider two functions that tend to positive infinity as the argument tends to zero from the right.
However, the same record of the result of taking the limit does not indicate their equality. The data of infinity of different order and this is confirmed by the absence of a finite limit in relation of one function to another.
In the non-standard analysis such simplifications are not permissible. The field of real numbers is expanded by introducing hyper-real numbers . Infinitesimals are represented in the form of the usual meaning - zero, but in the appendage the whole ejected “small things” are kept. For infinitely large potential infinity (two or one - it does not matter), is divided into many actual infinities . On the one hand, we complicate (we lose the possibility of absorption / neglect). On the other hand, we acquire the possibility of comparing infinitely small and infinitely large quantities. This means that we can consider infinity as numbers.
For functionthe current infinities to the left and right of zero are equal (by module, that is, not taking the sign into account), since:
- on both sides of the path (the number of elements that need to go) from zero to infinity is the same;
- the approximation algorithm (the formula in the form of a fraction) is the same;
- the minus sign in the algorithm does not affect the speed or acceleration of approaching infinity.
It should be noted that the specified criteria are arbitrary and are not given to the formal definitions of non-standard analysis.
For further discussion, the concept of actual infinity is no longer required. We return to the familiar world where we will operate on the concept of infinity, implying potential infinity.
Well, the limits are the same. Now, it seems, everything is ready to bridge the gap between them.

In the mathematical model using the projective extension of the number line , the division by zero is defined.
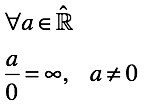
It seems that our problem is solved. However, we will not be in a hurry, let's see what the consequences are. In addition to the division, the following operations are defined in the system (recall that the infinity is unsigned).

Almost all of them with additional conditions, it is alarming. But let's not hurry, better look at the list of undefined operations:

Let's see how the distribution law will behave. Substitute in it certain values and perform the required operations.
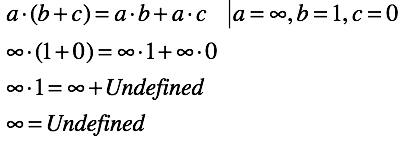
As a result, some of the identities cease to behave as we are used to. However, they did not disappear without a trace. The distribution law only works from right to left (i.e., in the case where the right-hand side of equality is defined). This is one of the clearest examples of negative consequences. Other identities are preserved in a more or less stable form.
Summing up:
- The usual behavior of identities has changed. To operate them, you need to not forget about the new additional conditions.
- The usual behavior of zero is distorted. We are accustomed to reasoning, if we take something zero times, then there will be zero. However, in this algebraic system, the product of zero at infinity is not defined. Accordingly, an algebraic expression with variables in which such an entry occurs, for example.
 , can not be simplified unilaterally.
, can not be simplified unilaterally. - The possibility of the usual comparison disappears. A more-or-less comparison is defined only on part of the space. For example, the comparison of real numbers with infinity is not defined.
- The resulting algebraic structure is not a field in terms of general algebra. Distributive law is violated (shown above). Also, there is no inverse element for infinity (the product of this element and infinity should give a unit). The latter can be considered as a consequence of the uncertainty of dividing infinity into infinity. But still it should be understood that this is a gross simplification. The strict definition of the inverse element is not related to the division operation.
The bottom line. Old approaches have stopped working. The complexity of the system, in the form of a heap “if”, “for all but”, etc., has increased. We had only two uncertainties 1/0 and 0/0 (we did not consider power operations), it became five. Disclosing one uncertainty gave rise to even more uncertainties.

1.2 Wheel
On the introduction of unsigned infinity, everything did not stop. In order to get out of the uncertainties need a second wind.
So, we have a set of real numbers and two uncertainties 1/0 and 0/0. To eliminate the first, we performed a projective extension of the number line (that is, we entered unsigned infinity). Let's try to deal with the second uncertainty of the form 0/0. Let's do the same. Let's add the set of numbers with a new element representing the second uncertainty.

The definition of a division operation is based on multiplication. It does not suit us. Let's unbind operations from each other, but keep the usual behavior for real numbers. We define a unary division operation, denoted by the sign "/".
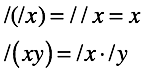
We will define operations.

This structure is called the “Wheel”. The term was taken because of the similarity with the topological picture of the projective extension of the numerical line and the point 0/0.

It seems everything looks good, but the devil is in the details:
- Multiplying ∞ or ⊥ by zero does not give zero. This leads to
 in general.
in general. - For ∞ and ⊥, there are no inverse elements for both binary operations. It means that
 by multiplication in the general case. As a consequence, it is not possible to introduce a binary division operation covering the entire space.
by multiplication in the general case. As a consequence, it is not possible to introduce a binary division operation covering the entire space. - Symmetrical addition situation,
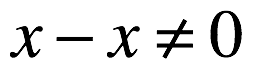 in general.
in general.
In order to stabilize all the features, in addition to the expansion of the set of elements, a bonus is attached in the form of not one, but two identities describing distribution law.
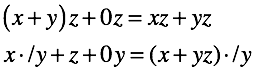
Mathematical language:
From the point of view of general algebra, we operated with a field . And in the field, as is known, only two operations are defined (addition and multiplication). The concept of division is derived through the inverse, and if even deeper, the unit elements. The changes make our algebraic system into a monoid both by the addition operation (with zero as a neutral element) and by the multiplication operation (with a unit as a neutral element).
In the works of the discoverers, the symbols ∞ and ⊥ are not always used. Instead, you can see the entry as / 0 and 0/0.
The world is no longer so beautiful, is it? Still, do not hurry. Check whether the new identities of the distribution law can cope with our extended set
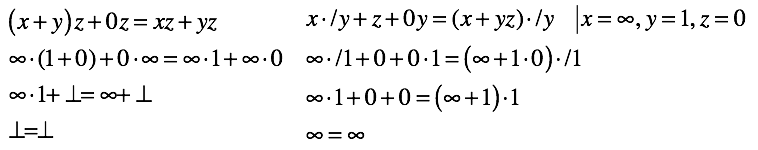
This time the result is much better.
Summing up:
- All operations are well defined and there is no possibility of "falling overboard."
- Elementary algebra is a special case of the wheel. If we drop the add-ins ∞ and ⊥ (that is, we can again assert that
 and
and 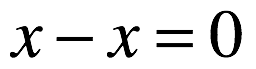 ), then all formulas will degenerate into familiar ones.
), then all formulas will degenerate into familiar ones. - Feels like everything that was “undefined” (Undefined) during projective extension was indicated by the symbol
 . This object also absorbs everything that it encounters as well as “undefined”. All the gaps where uncertainties appeared during the projective expansion were plugged with this object.
. This object also absorbs everything that it encounters as well as “undefined”. All the gaps where uncertainties appeared during the projective expansion were plugged with this object.
The bottom line. Algebra works fine. However, the notion of “undefined” was taken as a basis, which was considered to be something existing and operate with it. One day someone will say that everything is bad and you need to break this “undefined” into several more “undefined”, but smaller. General algebra will say: “No problem, Bro!”.
Approximately the additional (j and k) imaginary units in quaternions are postulated like this.
It is worth noting that there are other algebraic systems with division. For example, "meadows" (common meadows). They are slightly simpler, since they do not expand the space by introducing new elements. The goal is achieved as in the wheels, the transformation of the operations of addition and multiplication, as well as the rejection of binary division.
The ability to "move the unknown" for mathematics is the norm. But all these wrappers do not give an answer to the main question, what is there inside?

Useful literature
- Setzer, Anton (Drafts): Wheels, 1997 ( pdf )
- Carlström, Jesper: Wheels - on division by zero, 2001 ( pdf )
- PJ Potts: Exact Real Arithmetic using Möbius Transformations, 1998 ( pdf )
- Jan A. Bergstra & Alban Ponse: Division by Zero in Common Meadows ( pdf )
- A. Edalat and PJ Potts. A new representation for exact real numbers, 2000
- http://en.wikipedia.org/wiki/Undefined_(mathematics)
- http://en.wikipedia.org/wiki/Wheel_theory
- Forum dxdy - division by zero (2)
- Forum dxdy - division by zero is possible (12)
Source: https://habr.com/ru/post/247635/
All Articles