Correct polyhedra. Part 2. Foursome
Previous publication: Regular polyhedra. Part 1. Trimerie
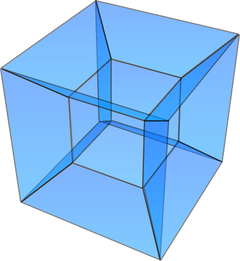
I see that at Habré serious people gathered. The article about trimerie on the account of "once" was dismantled. However, the spaces of constant curvature will not surprise anyone in our time. Nevertheless, there are always those who want to look higher in fourfold. Well, it is with such inquisitive colleagues that we continue the conversation and proceed to the next level in dimension.
My task is not just to tell about partitioning spaces of constant curvature of any dimension into regular polyhedra, but to make it so that even yesterday's schoolchildren who have completed 11 classes understand the material. I love the articles on Habré precisely because of their clarity, clarity, simplicity, despite the complexity of the material, and in the same quality I try to provide information in publications. In universities and in domestic publications, the proposed material may be considered, but, it seems to me, not in this form. I think that the information will be useful for students. In foreign literature, this material is, respectively, not in Russian, in a highly condensed form and using higher mathematics. Here I “chew” everything for schoolchildren, without higher mathematics, in fact, on one geometric intuition. We will see in the next article how the transition from 4D to 5D will be made using geometry, clearly, without higher algebra. This will be the most difficult step, but whoever understands it, will understand all the other dimensions from 6 and up. I'm not sure that I managed to “chew everything up thoroughly, so if there are additional questions - ask, this will help me improve the article.
')
In this publication, the idea of ​​the calculations is completely the same as in the previous article, only one dimension higher , so if someone has not had time to get acquainted with it , it is advisable to do this in order to understand what is happening.
First, we give all the definitions again, only for 4-dimensional polyhedra and the corresponding Schläfli symbol. I do not want to immediately give general formulations in order not to confuse unprepared readers who may be dealing with this subject for the first time. Then we give the problem statement. In this publication, it seems that she took a more strict and slender appearance. If I am mistaken in some details, then that's okay, this is not a paper publication, I will edit and correct it so that everything is beautiful. The basic calculations and the result are correct, do not worry about it, then even references to authoritative authors will give, if that. Looking to these authors you will understand that my work, in the form of these several publications, is not in vain.
In polyhedrons there are many different angles; we call the dihedral adjacent angle between adjacent faces, i.e. facets having a common edge.
I give the definition of a correct polyhedron recurrent in my own words, because Habr is not a place for copy-pasters.
A regular 4-dimensional polyhedron is a convex polyhedron, in which all 3-dimensional faces are regular polyhedra equal to each other and all angles between 3-dimensional faces are equal to each other.
There is a statement that the partition of the (n-1) -dimensional sphere is in one-to-one correspondence with a regular n-dimensional polyhedron, with n> 1. That is, the dimension of a polyhedron is one higher than the dimension of the sphere that we split. For example, if the vertices of the partition of a 3-dimensional sphere are joined by edges corresponding to the arcs of the partition, then we get a 4-dimensional polyhedron. I do not know how this statement is proved and whether it is proved at all. Therefore, it is taken as an axiom and we consider it to be true in all dimensions of spaces. For a two-dimensional sphere, using the icosahedron as an example, this was shown in a video clip in a previous publication. It can be said that in three dimensions (that is, for splitting a two-dimensional sphere), this fact was established experimentally, and in four dimensions and above, we believe that everything is the same. It seems that everything is clean here, it is intuitively clear that it is so.
The definition of the symbol Schläfli also give in your own words.
The Schläfli symbol is the sequence of numbers {p1, p2, p3} that defines the algorithm for constructing a regular polyhedron as follows:
- take the correct {p1} squares, combine them along the edges, so that each vertex matches p2 pieces of such {p1}, we get {{p1}, p2} or briefly {p1, p2}
- take, obtained at the previous step, {p1, p2} and merge them along flat faces so that each edge contains p3 pieces of such {p1, p2} three-dimensional polyhedra.
Induction already suggests itself in the definition, isn't it? A general definition for an n-dimensional regular polyhedron will be given in the next publication. For now, it is better to consider a special case in order to make it easier to understand and not be distracted by general formulations.
And one more thought (statement of the problem), which, expressed in a rough form, is not true, but it is not used in calculations, therefore it does not affect the result, but for that it is the driving force of research :) The idea is such that for any Schläfli symbol in any dimension There is a regular polyhedron that splits one of the spaces of constant curvature of the corresponding dimension. We saw that when splitting two-dimensional spaces this thought is true, there any Schläfli symbol broke something. The word "Exists" is capitalized because in reality this is not true for dimensions 4 and higher. Assuming the existence is always - this is of course liberty, but it is possible to formulate the statement of the problem in such a way that this thought will be legitimate, namely
the number of different values ​​of the Schläfli symbol is a countable set; split this set into non-intersecting subsets (classes) of finite or infinite types:
- the class of symbols defining the division of the Spherical space into regular polyhedra of the corresponding dimension;
- --- // --- splitting of Euclidean space --- // ---
- --- // --- partition of the Lobachevsky space into regular polyhedra of Finite volume --- // ---
- --- // --- partition of the Lobachevsky space into regular limit polyhedra of finite volume --- // --- (such, whose vertices fall directly on the absolute - the boundary of the Poincaré disk)
- --- // --- partition of the Lobachevsky space into regular polyhedra of infinite volume --- // --- (if the resulting figures are conventionally considered regular polyhedra)
- the class of “bad” characters that cannot be matched with some kind of polyhedron or some kind of partition of the space of constant curvature.
In enumerating these classes, we ran a little forward, and in the splits of Lobachevsky spaces, above, we identified three subsets (classes), instead of one, as for Sphere and Euclidean.
In other words, our task is to study all possible values ​​of the Schlefly symbol in all dimensions, in all three spaces of constant curvature. This is motivation, purpose and task. In this publication, the dimension of the partitioned spaces of constant curvature = 3, the dimension of the resulting polyhedra = 4.
The very idea of ​​the solution is simple, as in the previous article on three-measure, on the one hand, using the parameters of the Schläfli symbol {p1, p2}, we need to calculate the dihedral angle (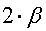
) polyhedron and compare this angle with 
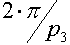those. to complete turnaround ( 
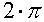) contained an integer number of polyhedra converged in the edge. Here p3 is the third parameter of the Schläfli symbol {p1, p2, p3}, which defines the partition of the 4-dimensional space into the polyhedra {p1, p2}, meaning the number of {p1, p2} polyhedra converged in the edge.
1. If it turns out that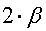 = 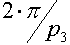it means that you do not need to bend space, everything came together beautifully, i.e. this is Euclidean space. As you can see, the deuce suggests reduction, therefore the dihedral angle of the polyhedron does not appear in the calculations. 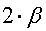and his half =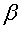 
2. If it turns out that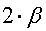 < 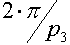those. the dihedral angle is small, then the polyhedron, along with its angles, must be “inflated” so that the angles increase to the desired values, it means that it should be placed on a three-dimensional sphere, i.e. This is a spherical case.
3. If it turns out that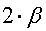 > 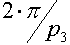those. the dihedral angle is large, then the polyhedron, along with its angles, must be “blown away” so that the angles are reduced to the desired values, it means you need to place it in the three-dimensional Lobachevsky space, i.e. This is a hyperbolic case.
About what it means to “blow up” and “blow off” a polyhedron (polygon) was described in the previous article, where we saw that the sum of the angles of a triangle (polygon) increases when we put it on a sphere, the triangle seems to swell and that the sum of angles the triangle is reduced when we put it in a hyperbolic space, the triangle seems to be deflated. There we saw it in two dimensions, everything similarly occurs with angles in 3-dimensional spaces and in spaces of higher dimensions.
However, if we know the angles of regular polygons by heart, then the dihedral angles of three-dimensional regular polyhedra are harder to memorize, although, of course, all these angles are known. We will see in the next publication, when we climb into the five-dimensional space, that derivation of the dihedral angle formula of a polyhedron becomes a non-trivial task and the formula itself comes to the fore. One could even name the article: the formula of the dihedral angle of a regular, convex polyhedron in n-dimensional Euclidean space. But in fact, this formula is not only the goal of the proposed publications, but also a means to help identify polyhedrons in spaces of higher dimensions. Those. All the questions here are closely related and interesting, each of them separately and all together, so choosing a concise title for these articles is really problematic.
Now it remains only to make calculations for calculating the dihedral angle by the parameters of the Schläfli symbol {p1, p2}, and compare the obtained values ​​with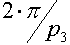 and write out the answer in the form of a table, and the student can. However, it is also not difficult to calculate the dihedral angle by the parameters p1, p2. Here in the next dimension, there is more difficult, there is already a highlight :) but more on that in the next publication.
I apologize, in the previous article I forgot about the auxiliary angles to say, which we will need for calculations. These are angles
and 
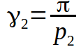. Who carefully read the previous article, he noticed that there was a corner on the drawing 
was designated, calculated and turned out 
. There we measured the angle of a regular polygon at vertex C. Now, taking this vertex and the two vertices adjacent to it, we obtain an isosceles triangle, - this is the angle at the base of this triangle, now we need it. Also for the 3-dimensional polyhedron we need an angle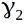 
Is the angle at the base of an isosceles triangle, at a regular polygon {p2} lying at the base of an isosceles pyramid. The pyramid is obtained by cutting off {p1, p2} of one vertex under study, along the plane of nearby vertices. Pay attention to the simple but important fact that since at the top of the pyramid the p2 pieces of regular p1-gons converge, then at the base of this pyramid a correct p2-gon is obtained. This is what we use to calculate the angle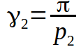
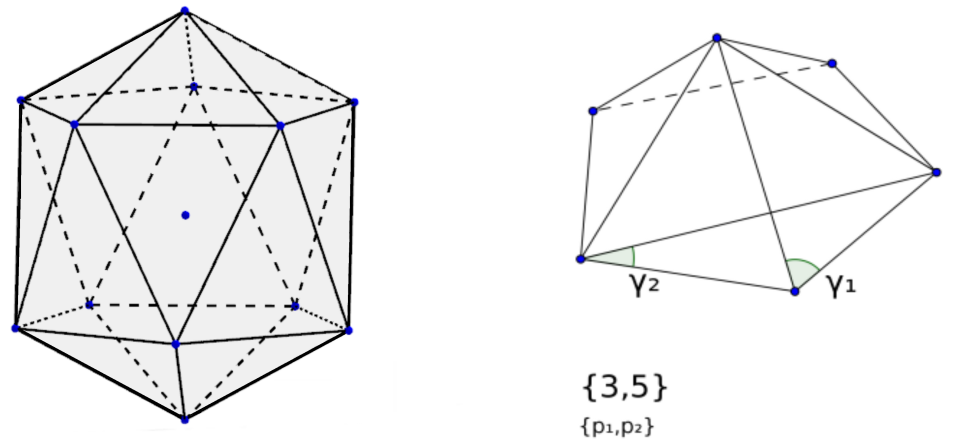
The figure shows an example with the icosahedron, here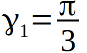
, 
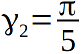in the general case for an arbitrary {p1, p2}, we obtain , 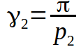. So far, we are in Euclidean space, so the sum of the angles of the triangle is still equal 
.
Now consider this isosceles pyramid closer. To calculate the dihedral angle, it is enough to consider not the whole pyramid, but only one edge and two faces containing this edge.
In the general case for {p1, p2} we consider the edge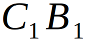
and find 
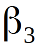this is half the angle we are looking for, i.e. half dihedral angle of the polyhedron {p1, p2}. I will give an explanation about the additional constructions: 
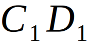and 
- heights in the corresponding isosceles triangles. Isosceles triangle plane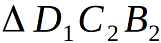 
- orthogonal to the edge 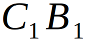by construction, therefore a flat angle 
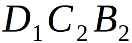this triangle is equal in magnitude to the desired dihedral angle of the regular polyhedron {p1, p2}. Not complicated calculations are written to the left of the drawing, please read them carefully. If you know the definition of sine and cosine, then difficulties should not arise. So:
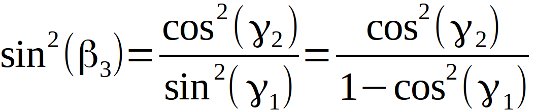
You can, of course, calculate this angle through the fundamental tetrahedron (with the vertices in the center of the 3D face, the center of the 2D face, the middle of the edge and the vertex of the polyhedron), so the classics do, but then the transition along the dimensions becomes difficult, in any case, it is unlikely for schoolchildren whether it will be possible to clarify. Therefore, the approach proposed in this publication, to the calculation of the dihedral angle, was deliberately chosen. At least this is another way to calculate this angle. Someone clearer one way, someone else.
As said, compare the angle with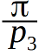
and write the comparison results as a table. Comparisons are more convenient to perform not for the angles themselves, but for the sines in the square of these angles, so as not to clutter the recording with arcsines, since this is the formula for the betta.
The essence of comparison in the form of the formula:
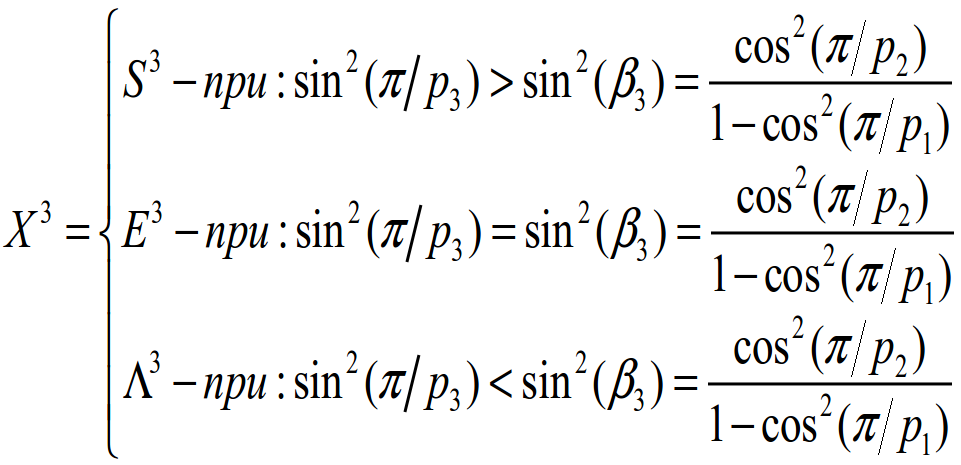
where X ^ 3 is the general designation of spaces of constant curvature, S ^ 3 is the three-dimensional sphere, E ^ 3 is the Euclidean three-dimensional space, Λ ^ 3 is the three-dimensional Lobachevsky space.
The result of the comparison in the form of a table:
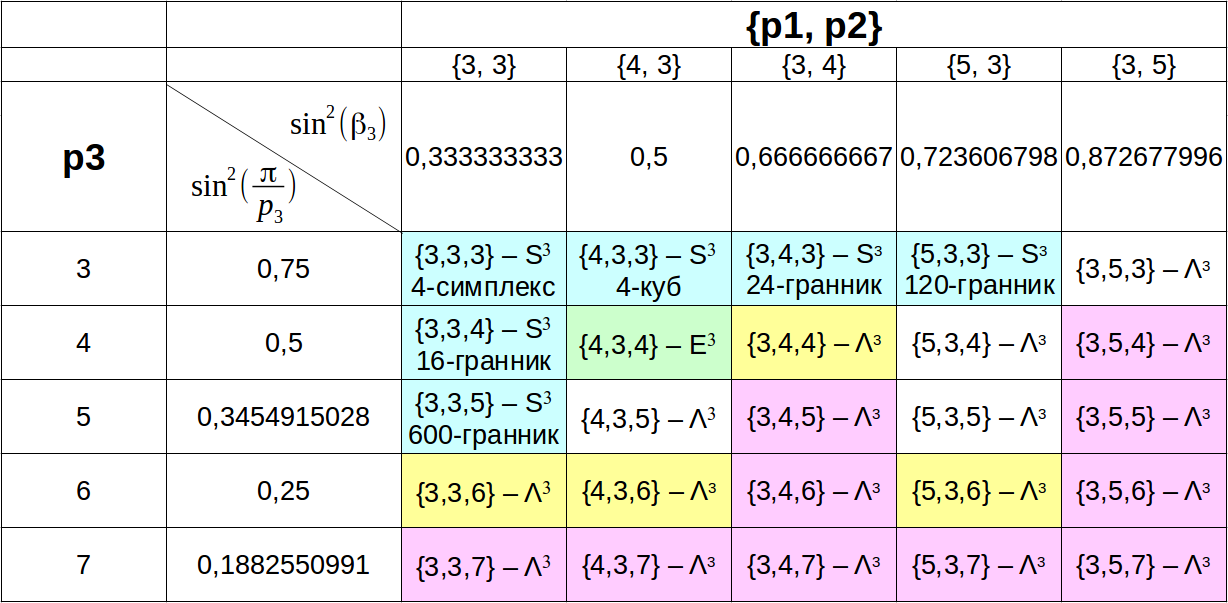
Where:
Once again a small explanation - the second column is compared, for
and the third line, for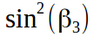 
. For example:
1. the column {4,3} is compared with the line p3 = 4, we get 0.5 = 0.5 - it means {4,3,4} - it breaks the Euclidean 3-dimensional space, these are usual cubes converging on 4 in the edge. :) Elementary.
2. For the column {3,3} and the row p3 = 3 we have 0.5 <0.75 - it means {3,3,3} - it breaks the 3-dimensional sphere (and it corresponds to a 4-dimensional polyhedron).
3. For the column {5,3} and the row p3 = 6 we have 0.723> 0.25 - it means {5,3,6} - it divides the 3-dimensional Lobachevsky space into a regular, limit polyhedron. The limit can be understood by the fact that it has a vertex figure {p2, p3} = {3,6} - it breaks the two-dimensional Euclidean space, i.e. Euclidean plane.
In the general case, if {p1, p2, p3} splits the Lobachevsky space, then the vertex figure plays the role:
- if {p2, p3} breaks Euclidean, then {p1, p2, p3} is a limit polyhedron,
- if {p2, p3} - breaks a sphere, then {p1, p2, p3} - has a finite volume and size,
- if {p2, p3} - breaks the Lobachevsky plane, then {p1, p2, p3} - has infinite volume.
This statement is without proof, I think that it is true and I know why, but I can’t prove and show strictly and simply. It includes the horosphere, on the surface of which is Euclidean geometry. And the vertex figure just cuts off the horosphere for the limit polyhedron.
So, we learned how to calculate the dihedral angle of a regular polyhedron by its Schläfli symbol {p1, p2}, just in case I’ll write again:
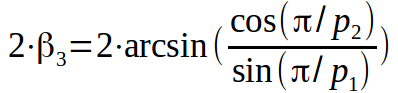
And they found 6 partitions of the three-dimensional sphere into regular three-dimensional polyhedra:
{3,3,3} - tetrahedra that converged on 3 in the edge,
{4,3,3} - cubes converged by 3 in the edge,
{3,3,4} - tetrahedra that converge in 4 in the edge,
{3,4,3} - octahedra converged by 3 in the edge,
{5,3,3} - dodecahedrons that converged in edge 3,
{3,3,5} - tetrahedrons that converge in 5 in the edge.
And this means that there are 6 corresponding regular 4-dimensional polyhedra with the same Schläfli symbols. It is true to count in general terms the number of vertices, edges, faces and facets of these polyhedra is not as easy as it seems at first glance. In special cases for a 4-tetrahedron, 4-cube, 4-octahedron (orthohedron) this can be done by induction, but for the other polyhedra this trick does not work.
Unfortunately, I do not have my own pictures of these polyhedra, so I refer to Wikipedia , there are beautiful pictures for fourfolds.
Just as when we look at a notebook in a cell (partitioning {4, 4}), we see the structure, as if the Euclidean plane itself has the structure {4, 4}, we already know that there are only two structures of the same plane { 3, 6} and {6, 3}. Now we have learned that the partition of the 3-dimensional Euclidean space is unique {4, 3, 4} - into cubes converging 4 pieces in the edge. We visualize this partition and feel the structure of this space. Now let us imagine mentally {5, 3} - dodecahedrons, attach them to each other along flat faces (pentagons), 3 such dodecahedrons converge in an edge and there is still a gap. Now mentally evenly inflate these dodecahedrons until the gap disappears. When it disappears, exactly 3 dodecahedrons will converge in the edge. Now mentally add up three dodecahedrons in each edge. In all the edges at the same time it is more difficult to imagine, but necessary. If we take 120 such bloated dodecahedrons and attach them all without gaps between each other along the faces, then we obtain a closed partition of the 3-dimensional sphere. You can also imagine with the other 5 partitions of the 3-dimensional sphere. Such reasonable experiments with polyhedra help to mentally understand the structure of the 3-dimensional sphere and to touch the 4-dimensional Euclidean space. Similarly, one can ponder with hyperbolic 3-dimensional space. The calculations given in the publication help us to understand what space we are in for a given Schläfli symbol, i.e. for a given mental construction.
In the next post we will do the same thing only one dimension higher. I think that I will give there a video clip explaining the main idea of ​​the transition (rise) by dimensions. If someone else does not understand what is happening, then maybe this video will shed light on all the calculations done here and in the previous article.
If everything is clear, then go to the next level by dimension.
References:
Correct polyhedra. Part 1. Trimerie
Correct polyhedra. Part 2. Foursome
Correct polyhedra. Part 2.5 (auxiliary)
Schläfli symbol. Part 2.6
Introduction
I see that at Habré serious people gathered. The article about trimerie on the account of "once" was dismantled. However, the spaces of constant curvature will not surprise anyone in our time. Nevertheless, there are always those who want to look higher in fourfold. Well, it is with such inquisitive colleagues that we continue the conversation and proceed to the next level in dimension.
My task is not just to tell about partitioning spaces of constant curvature of any dimension into regular polyhedra, but to make it so that even yesterday's schoolchildren who have completed 11 classes understand the material. I love the articles on Habré precisely because of their clarity, clarity, simplicity, despite the complexity of the material, and in the same quality I try to provide information in publications. In universities and in domestic publications, the proposed material may be considered, but, it seems to me, not in this form. I think that the information will be useful for students. In foreign literature, this material is, respectively, not in Russian, in a highly condensed form and using higher mathematics. Here I “chew” everything for schoolchildren, without higher mathematics, in fact, on one geometric intuition. We will see in the next article how the transition from 4D to 5D will be made using geometry, clearly, without higher algebra. This will be the most difficult step, but whoever understands it, will understand all the other dimensions from 6 and up. I'm not sure that I managed to “chew everything up thoroughly, so if there are additional questions - ask, this will help me improve the article.
')
In this publication, the idea of ​​the calculations is completely the same as in the previous article, only one dimension higher , so if someone has not had time to get acquainted with it , it is advisable to do this in order to understand what is happening.
First, we give all the definitions again, only for 4-dimensional polyhedra and the corresponding Schläfli symbol. I do not want to immediately give general formulations in order not to confuse unprepared readers who may be dealing with this subject for the first time. Then we give the problem statement. In this publication, it seems that she took a more strict and slender appearance. If I am mistaken in some details, then that's okay, this is not a paper publication, I will edit and correct it so that everything is beautiful. The basic calculations and the result are correct, do not worry about it, then even references to authoritative authors will give, if that. Looking to these authors you will understand that my work, in the form of these several publications, is not in vain.
Definitions Axioms. Formulation of the problem
In polyhedrons there are many different angles; we call the dihedral adjacent angle between adjacent faces, i.e. facets having a common edge.
I give the definition of a correct polyhedron recurrent in my own words, because Habr is not a place for copy-pasters.
A regular 4-dimensional polyhedron is a convex polyhedron, in which all 3-dimensional faces are regular polyhedra equal to each other and all angles between 3-dimensional faces are equal to each other.
There is a statement that the partition of the (n-1) -dimensional sphere is in one-to-one correspondence with a regular n-dimensional polyhedron, with n> 1. That is, the dimension of a polyhedron is one higher than the dimension of the sphere that we split. For example, if the vertices of the partition of a 3-dimensional sphere are joined by edges corresponding to the arcs of the partition, then we get a 4-dimensional polyhedron. I do not know how this statement is proved and whether it is proved at all. Therefore, it is taken as an axiom and we consider it to be true in all dimensions of spaces. For a two-dimensional sphere, using the icosahedron as an example, this was shown in a video clip in a previous publication. It can be said that in three dimensions (that is, for splitting a two-dimensional sphere), this fact was established experimentally, and in four dimensions and above, we believe that everything is the same. It seems that everything is clean here, it is intuitively clear that it is so.
The definition of the symbol Schläfli also give in your own words.
The Schläfli symbol is the sequence of numbers {p1, p2, p3} that defines the algorithm for constructing a regular polyhedron as follows:
- take the correct {p1} squares, combine them along the edges, so that each vertex matches p2 pieces of such {p1}, we get {{p1}, p2} or briefly {p1, p2}
- take, obtained at the previous step, {p1, p2} and merge them along flat faces so that each edge contains p3 pieces of such {p1, p2} three-dimensional polyhedra.
Induction already suggests itself in the definition, isn't it? A general definition for an n-dimensional regular polyhedron will be given in the next publication. For now, it is better to consider a special case in order to make it easier to understand and not be distracted by general formulations.
And one more thought (statement of the problem), which, expressed in a rough form, is not true, but it is not used in calculations, therefore it does not affect the result, but for that it is the driving force of research :) The idea is such that for any Schläfli symbol in any dimension There is a regular polyhedron that splits one of the spaces of constant curvature of the corresponding dimension. We saw that when splitting two-dimensional spaces this thought is true, there any Schläfli symbol broke something. The word "Exists" is capitalized because in reality this is not true for dimensions 4 and higher. Assuming the existence is always - this is of course liberty, but it is possible to formulate the statement of the problem in such a way that this thought will be legitimate, namely
the number of different values ​​of the Schläfli symbol is a countable set; split this set into non-intersecting subsets (classes) of finite or infinite types:
- the class of symbols defining the division of the Spherical space into regular polyhedra of the corresponding dimension;
- --- // --- splitting of Euclidean space --- // ---
- --- // --- partition of the Lobachevsky space into regular polyhedra of Finite volume --- // ---
- --- // --- partition of the Lobachevsky space into regular limit polyhedra of finite volume --- // --- (such, whose vertices fall directly on the absolute - the boundary of the Poincaré disk)
- --- // --- partition of the Lobachevsky space into regular polyhedra of infinite volume --- // --- (if the resulting figures are conventionally considered regular polyhedra)
- the class of “bad” characters that cannot be matched with some kind of polyhedron or some kind of partition of the space of constant curvature.
In enumerating these classes, we ran a little forward, and in the splits of Lobachevsky spaces, above, we identified three subsets (classes), instead of one, as for Sphere and Euclidean.
In other words, our task is to study all possible values ​​of the Schlefly symbol in all dimensions, in all three spaces of constant curvature. This is motivation, purpose and task. In this publication, the dimension of the partitioned spaces of constant curvature = 3, the dimension of the resulting polyhedra = 4.
The idea of ​​solving the problem
The very idea of ​​the solution is simple, as in the previous article on three-measure, on the one hand, using the parameters of the Schläfli symbol {p1, p2}, we need to calculate the dihedral angle (
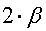) polyhedron and compare this angle with 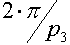those. to complete turnaround ( 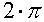) contained an integer number of polyhedra converged in the edge. Here p3 is the third parameter of the Schläfli symbol {p1, p2, p3}, which defines the partition of the 4-dimensional space into the polyhedra {p1, p2}, meaning the number of {p1, p2} polyhedra converged in the edge.1. If it turns out that
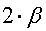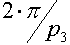= it means that you do not need to bend space, everything came together beautifully, i.e. this is Euclidean space. As you can see, the deuce suggests reduction, therefore the dihedral angle of the polyhedron does not appear in the calculations. 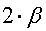and his half =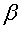 2. If it turns out that
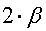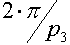< those. the dihedral angle is small, then the polyhedron, along with its angles, must be “inflated” so that the angles increase to the desired values, it means that it should be placed on a three-dimensional sphere, i.e. This is a spherical case.3. If it turns out that
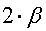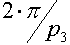> those. the dihedral angle is large, then the polyhedron, along with its angles, must be “blown away” so that the angles are reduced to the desired values, it means you need to place it in the three-dimensional Lobachevsky space, i.e. This is a hyperbolic case.About what it means to “blow up” and “blow off” a polyhedron (polygon) was described in the previous article, where we saw that the sum of the angles of a triangle (polygon) increases when we put it on a sphere, the triangle seems to swell and that the sum of angles the triangle is reduced when we put it in a hyperbolic space, the triangle seems to be deflated. There we saw it in two dimensions, everything similarly occurs with angles in 3-dimensional spaces and in spaces of higher dimensions.
However, if we know the angles of regular polygons by heart, then the dihedral angles of three-dimensional regular polyhedra are harder to memorize, although, of course, all these angles are known. We will see in the next publication, when we climb into the five-dimensional space, that derivation of the dihedral angle formula of a polyhedron becomes a non-trivial task and the formula itself comes to the fore. One could even name the article: the formula of the dihedral angle of a regular, convex polyhedron in n-dimensional Euclidean space. But in fact, this formula is not only the goal of the proposed publications, but also a means to help identify polyhedrons in spaces of higher dimensions. Those. All the questions here are closely related and interesting, each of them separately and all together, so choosing a concise title for these articles is really problematic.
Now it remains only to make calculations for calculating the dihedral angle by the parameters of the Schläfli symbol {p1, p2}, and compare the obtained values ​​with
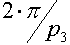and write out the answer in the form of a table, and the student can. However, it is also not difficult to calculate the dihedral angle by the parameters p1, p2. Here in the next dimension, there is more difficult, there is already a highlight :) but more on that in the next publication.Calculation of the dihedral angle for a regular polyhedron {p1, p2}
I apologize, in the previous article I forgot about the auxiliary angles to say, which we will need for calculations. These are angles
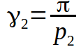and . Who carefully read the previous article, he noticed that there was a corner on the drawing was designated, calculated and turned out . There we measured the angle of a regular polygon at vertex C. Now, taking this vertex and the two vertices adjacent to it, we obtain an isosceles triangle, - this is the angle at the base of this triangle, now we need it. Also for the 3-dimensional polyhedron we need an angle 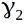Is the angle at the base of an isosceles triangle, at a regular polygon {p2} lying at the base of an isosceles pyramid. The pyramid is obtained by cutting off {p1, p2} of one vertex under study, along the plane of nearby vertices. Pay attention to the simple but important fact that since at the top of the pyramid the p2 pieces of regular p1-gons converge, then at the base of this pyramid a correct p2-gon is obtained. This is what we use to calculate the angle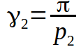 The figure shows an example with the icosahedron, here
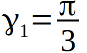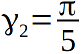, in the general case for an arbitrary {p1, p2}, we obtain , 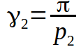. So far, we are in Euclidean space, so the sum of the angles of the triangle is still equal .Now consider this isosceles pyramid closer. To calculate the dihedral angle, it is enough to consider not the whole pyramid, but only one edge and two faces containing this edge.
In the general case for {p1, p2} we consider the edge
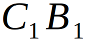and find 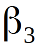this is half the angle we are looking for, i.e. half dihedral angle of the polyhedron {p1, p2}. I will give an explanation about the additional constructions: 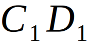and - heights in the corresponding isosceles triangles. Isosceles triangle plane 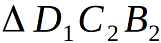- orthogonal to the edge 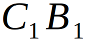by construction, therefore a flat angle 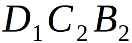this triangle is equal in magnitude to the desired dihedral angle of the regular polyhedron {p1, p2}. Not complicated calculations are written to the left of the drawing, please read them carefully. If you know the definition of sine and cosine, then difficulties should not arise. So: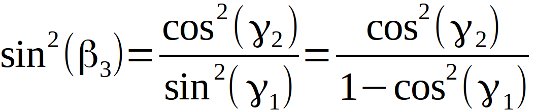You can, of course, calculate this angle through the fundamental tetrahedron (with the vertices in the center of the 3D face, the center of the 2D face, the middle of the edge and the vertex of the polyhedron), so the classics do, but then the transition along the dimensions becomes difficult, in any case, it is unlikely for schoolchildren whether it will be possible to clarify. Therefore, the approach proposed in this publication, to the calculation of the dihedral angle, was deliberately chosen. At least this is another way to calculate this angle. Someone clearer one way, someone else.
Calculating and comparing angles
As said, compare the angle with
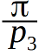and write the comparison results as a table. Comparisons are more convenient to perform not for the angles themselves, but for the sines in the square of these angles, so as not to clutter the recording with arcsines, since this is the formula for the betta.The essence of comparison in the form of the formula:
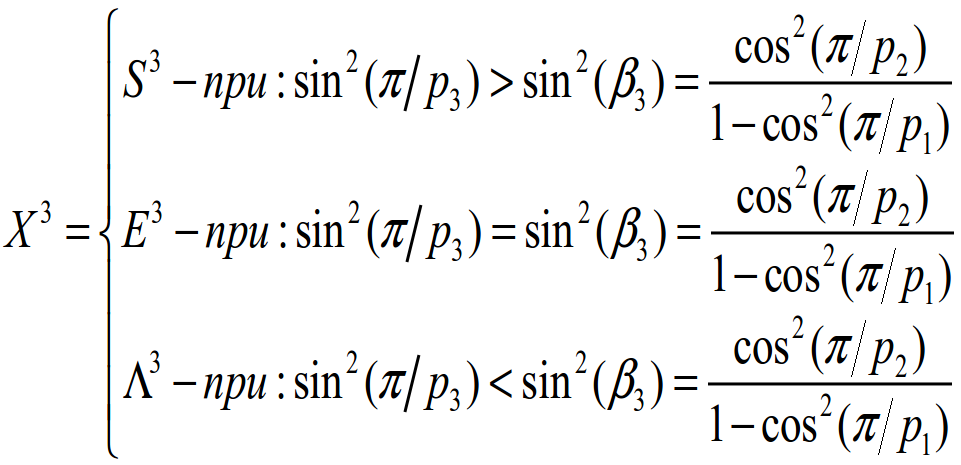
where X ^ 3 is the general designation of spaces of constant curvature, S ^ 3 is the three-dimensional sphere, E ^ 3 is the Euclidean three-dimensional space, Λ ^ 3 is the three-dimensional Lobachevsky space.
The result of the comparison in the form of a table:
Where:
Once again a small explanation - the second column is compared, for
and the third line, for 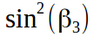. For example:1. the column {4,3} is compared with the line p3 = 4, we get 0.5 = 0.5 - it means {4,3,4} - it breaks the Euclidean 3-dimensional space, these are usual cubes converging on 4 in the edge. :) Elementary.
2. For the column {3,3} and the row p3 = 3 we have 0.5 <0.75 - it means {3,3,3} - it breaks the 3-dimensional sphere (and it corresponds to a 4-dimensional polyhedron).
3. For the column {5,3} and the row p3 = 6 we have 0.723> 0.25 - it means {5,3,6} - it divides the 3-dimensional Lobachevsky space into a regular, limit polyhedron. The limit can be understood by the fact that it has a vertex figure {p2, p3} = {3,6} - it breaks the two-dimensional Euclidean space, i.e. Euclidean plane.
In the general case, if {p1, p2, p3} splits the Lobachevsky space, then the vertex figure plays the role:
- if {p2, p3} breaks Euclidean, then {p1, p2, p3} is a limit polyhedron,
- if {p2, p3} - breaks a sphere, then {p1, p2, p3} - has a finite volume and size,
- if {p2, p3} - breaks the Lobachevsky plane, then {p1, p2, p3} - has infinite volume.
This statement is without proof, I think that it is true and I know why, but I can’t prove and show strictly and simply. It includes the horosphere, on the surface of which is Euclidean geometry. And the vertex figure just cuts off the horosphere for the limit polyhedron.
Summarizing
So, we learned how to calculate the dihedral angle of a regular polyhedron by its Schläfli symbol {p1, p2}, just in case I’ll write again:
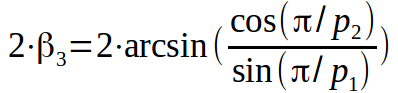
And they found 6 partitions of the three-dimensional sphere into regular three-dimensional polyhedra:
{3,3,3} - tetrahedra that converged on 3 in the edge,
{4,3,3} - cubes converged by 3 in the edge,
{3,3,4} - tetrahedra that converge in 4 in the edge,
{3,4,3} - octahedra converged by 3 in the edge,
{5,3,3} - dodecahedrons that converged in edge 3,
{3,3,5} - tetrahedrons that converge in 5 in the edge.
And this means that there are 6 corresponding regular 4-dimensional polyhedra with the same Schläfli symbols. It is true to count in general terms the number of vertices, edges, faces and facets of these polyhedra is not as easy as it seems at first glance. In special cases for a 4-tetrahedron, 4-cube, 4-octahedron (orthohedron) this can be done by induction, but for the other polyhedra this trick does not work.
Unfortunately, I do not have my own pictures of these polyhedra, so I refer to Wikipedia , there are beautiful pictures for fourfolds.
Just as when we look at a notebook in a cell (partitioning {4, 4}), we see the structure, as if the Euclidean plane itself has the structure {4, 4}, we already know that there are only two structures of the same plane { 3, 6} and {6, 3}. Now we have learned that the partition of the 3-dimensional Euclidean space is unique {4, 3, 4} - into cubes converging 4 pieces in the edge. We visualize this partition and feel the structure of this space. Now let us imagine mentally {5, 3} - dodecahedrons, attach them to each other along flat faces (pentagons), 3 such dodecahedrons converge in an edge and there is still a gap. Now mentally evenly inflate these dodecahedrons until the gap disappears. When it disappears, exactly 3 dodecahedrons will converge in the edge. Now mentally add up three dodecahedrons in each edge. In all the edges at the same time it is more difficult to imagine, but necessary. If we take 120 such bloated dodecahedrons and attach them all without gaps between each other along the faces, then we obtain a closed partition of the 3-dimensional sphere. You can also imagine with the other 5 partitions of the 3-dimensional sphere. Such reasonable experiments with polyhedra help to mentally understand the structure of the 3-dimensional sphere and to touch the 4-dimensional Euclidean space. Similarly, one can ponder with hyperbolic 3-dimensional space. The calculations given in the publication help us to understand what space we are in for a given Schläfli symbol, i.e. for a given mental construction.
In the next post we will do the same thing only one dimension higher. I think that I will give there a video clip explaining the main idea of ​​the transition (rise) by dimensions. If someone else does not understand what is happening, then maybe this video will shed light on all the calculations done here and in the previous article.
If everything is clear, then go to the next level by dimension.
References:
Correct polyhedra. Part 1. Trimerie
Correct polyhedra. Part 2. Foursome
Correct polyhedra. Part 2.5 (auxiliary)
Schläfli symbol. Part 2.6
Source: https://habr.com/ru/post/247505/
All Articles